Skip to main content
Journal of Inequalities and Applications
Download PDF
  • Research Article
  • Open access
  • Published:

Outer measures and weak type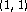 estimates of Hardy-Littlewood maximal operators

Journal of Inequalities and Applications volume 2006, Article number: 15063 (2006) Cite this article

Abstract

We will introduce the times modified centered and uncentered Hardy-Littlewood maximal operators on nonhomogeneous spaces for. We will prove that the times modified centered Hardy-Littlewood maximal operator is weak type bounded with constant when if the Radon measure of the space has "continuity" in some sense. In the proof, we will use the outer measure associated with the Radon measure. We will also prove other results of Hardy-Littlewood maximal operators on homogeneous spaces and on the real line by using outer measures.

[1234567891011121314]

References

  1. Bernal A: A note on the one-dimensional maximal function. Proceedings of the Royal Society of Edinburgh. Section A. Mathematics 1989,111(3–4):325–328. 10.1017/S030821050001859X

    Article  MATH  MathSciNet  Google Scholar 

  2. Calderón A-P: Inequalities for the maximal function relative to a metric. Studia Mathematica 1976,57(3):297–306.

    MATH  MathSciNet  Google Scholar 

  3. Carlsson H: A new proof of the Hardy-Littlewood maximal theorem. The Bulletin of the London Mathematical Society 1984,16(6):595–596. 10.1112/blms/16.6.595

    Article  MATH  MathSciNet  Google Scholar 

  4. Coifman RR, Weiss G: Analyse harmonique non-commutative sur certains espaces homogènes, Lecture Notes in Mathematics. Volume 242. Springer, Berlin; 1971:v+160.

    Google Scholar 

  5. Evans LC, Gariepy RF: Measure Theory and Fine Properties of Functions, Studies in Advanced Mathematics. CRC Press, Florida; 1992:viii+268.

    Google Scholar 

  6. Hardy GH, Littlewood JE: A maximal theorem with function-theoretic applications. Acta Mathematica 1930, 54: 81–116. 10.1007/BF02547518

    Article  MATH  MathSciNet  Google Scholar 

  7. Melas AD: The best constant for the centered Hardy-Littlewood maximal inequality. Annals of Mathematics. Second Series 2003,157(2):647–688. 10.4007/annals.2003.157.647

    Article  MATH  MathSciNet  Google Scholar 

  8. Muckenhoupt B, Stein EM: Classical expansions and their relation to conjugate harmonic functions. Transactions of the American Mathematical Society 1965, 118: 17–92.

    Article  MATH  MathSciNet  Google Scholar 

  9. Nazarov F, Treil S, Volberg A: Weak type estimates and Cotlar inequalities for Calderón-Zygmund operators on nonhomogeneous spaces. International Mathematics Research Notices 1998,1998(9):463–487. 10.1155/S1073792898000312

    Article  MATH  MathSciNet  Google Scholar 

  10. Sawano Y: Sharp estimates of the modified Hardy-Littlewood maximal operator on the nonhomogeneous space via covering lemmas. Hokkaido Mathematical Journal 2005, 34: 435–458.

    Article  MATH  MathSciNet  Google Scholar 

  11. Sierpinski W: Un lemme métrique. Fundamenta Mathematicae 1923, 4: 201–203.

    MATH  MathSciNet  Google Scholar 

  12. Termini D, Vitanza C: Weighted estimates for the Hardy-Littlewood maximal operator and Dirac deltas. The Bulletin of the London Mathematical Society 1990,22(4):367–374. 10.1112/blms/22.4.367

    Article  MATH  MathSciNet  Google Scholar 

  13. Trinidad Menarguez M, Soria F: Weak typeinequalities of maximal convolution operators. Rendiconti del Circolo Matematico di Palermo. Serie II 1992,41(3):342–352. 10.1007/BF02848939

    Article  MATH  MathSciNet  Google Scholar 

  14. Wiener N: The ergodic theorem. Duke Mathematical Journal 1939, 5: 1–18. 10.1215/S0012-7094-39-00501-6

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Hokkaido University, Sapporo, 060-0810, Japan

    Yutaka Terasawa

Authors
  1. Yutaka Terasawa
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yutaka Terasawa.

Rights and permissions

Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Reprints and permissions

About this article

Cite this article

Terasawa, Y. Outer measures and weak type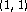 estimates of Hardy-Littlewood maximal operators. J Inequal Appl 2006, 15063 (2006). https://doi.org/10.1155/JIA/2006/15063

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1155/JIA/2006/15063

Keywords