- Research Article
- Open access
- Published:
Boundedness and Nonemptiness of Solution Sets for Set-Valued Vector Equilibrium Problems with an Application
Journal of Inequalities and Applications volume 2011, Article number: 936428 (2011)
Abstract
This paper is devoted to the characterizations of the boundedness and nonemptiness of solution sets for set-valued vector equilibrium problems in reflexive Banach spaces, when both the mapping and the constraint set are perturbed by different parameters. By using the properties of recession cones, several equivalent characterizations are given for the set-valued vector equilibrium problems to have nonempty and bounded solution sets. As an application, the stability of solution set for the set-valued vector equilibrium problem in a reflexive Banach space is also given. The results presented in this paper generalize and extend some known results in Fan and Zhong (2008), He (2007), and Zhong and Huang (2010).
1. Introduction
Let  and
and  be reflexive Banach spaces. Let
be reflexive Banach spaces. Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . Let
. Let  be a set-valued mapping with nonempty values. Let
be a set-valued mapping with nonempty values. Let  be a closed convex pointed cone in
be a closed convex pointed cone in  with
with  . The cone
. The cone  induces a partial ordering in
induces a partial ordering in  , which was defined by
, which was defined by  . We consider the following set-valued vector equilibrium problem, denoted by SVEP
. We consider the following set-valued vector equilibrium problem, denoted by SVEP , which consists in finding
, which consists in finding  such that
such that

It is well known that (1.1) is closely related to the following dual set-valued vector equilibrium problem, denoted by DSVEP , which consists in finding
, which consists in finding  such that
such that

We denote the solution sets of SVEP and DSVEP
and DSVEP by
by  and
and  , respectively.
, respectively.
Let  and
and  be two metric spaces. Suppose that a nonempty closed convex set
be two metric spaces. Suppose that a nonempty closed convex set  is perturbed by a parameter
is perturbed by a parameter  , which varies over
, which varies over  , that is,
, that is,  is a set-valued mapping with nonempty closed convex values. Assume that a set-valued mapping
is a set-valued mapping with nonempty closed convex values. Assume that a set-valued mapping  is perturbed by a parameter
is perturbed by a parameter  , which varies over
, which varies over  , that is,
, that is,  . We consider a parametric set-valued vector equilibrium problem, denoted by SVEP
. We consider a parametric set-valued vector equilibrium problem, denoted by SVEP , which consists in finding
, which consists in finding  such that
such that

Similarly, we consider the parameterized dual set-valued vector equilibrium problem, denoted by DSVEP , which consists in finding
, which consists in finding  such that
such that

We denote the solution sets of SVEP and DSVEP
and DSVEP by
by  and
and  , respectively.
, respectively.
In 1980, Giannessi [1] extended classical variational inequalities to the case of vector-valued functions. Meanwhile, vector variational inequalities have been researched quite extensively (see, e.g., [2]). Inspired by the study of vector variational inequalities, more general equilibrium problems [3] have been extended to the case of vector-valued bifunctions, known as vector equilibrium problems. It is well known that the vector equilibrium problem provides a unified model of several problems, for example, vector optimization, vector variational inequality, vector complementarity problem, and vector saddle point problem (see [4–9]). In recent years, the vector equilibrium problem has been intensively studied by many authors (see, e.g., [1–3, 10–26] and the references therein).
Among many desirable properties of the solution sets for vector equilibrium problems, stability analysis of solution set is of considerable interest (see, e.g, [27–33] and the references therein). Assuming that the barrier cone of  has nonempty interior, McLinden [34] presented a comprehensive study of the stability of the solution set of the variational inequality, when the mapping is a maximal monotone set-valued mapping. Adly [35], Adly et al. [36], and Addi et al. [37] discussed the stability of the solution set of a so-called semicoercive variational inequality. He [38] studied the stability of variational inequality problem with either the mapping or the constraint set perturbed in reflexive Banach spaces. Recently, Fan and Zhong [39] extended the corresponding results of He [38] to the case that the perturbation was imposed on the mapping and the constraint set simultaneously. Very recently, Zhong and Huang [40] studied the stability analysis for a class of Minty mixed variational inequalities in reflexive Banach spaces, when both the mapping and the constraint set are perturbed. They got a stability result for the Minty mixed variational inequality with
has nonempty interior, McLinden [34] presented a comprehensive study of the stability of the solution set of the variational inequality, when the mapping is a maximal monotone set-valued mapping. Adly [35], Adly et al. [36], and Addi et al. [37] discussed the stability of the solution set of a so-called semicoercive variational inequality. He [38] studied the stability of variational inequality problem with either the mapping or the constraint set perturbed in reflexive Banach spaces. Recently, Fan and Zhong [39] extended the corresponding results of He [38] to the case that the perturbation was imposed on the mapping and the constraint set simultaneously. Very recently, Zhong and Huang [40] studied the stability analysis for a class of Minty mixed variational inequalities in reflexive Banach spaces, when both the mapping and the constraint set are perturbed. They got a stability result for the Minty mixed variational inequality with  -pseudomonotone mapping in a reflexive Banach space, when both the mapping and the constraint set are perturbed by different parameters, which generalized and extended some known results in [38, 39].
-pseudomonotone mapping in a reflexive Banach space, when both the mapping and the constraint set are perturbed by different parameters, which generalized and extended some known results in [38, 39].
Inspired and motivated by the works mentioned above, in this paper, we further study the characterizations of the boundedness and nonemptiness of solution sets for set-valued vector equilibrium problems in reflexive Banach spaces, when both the mapping and the constraint set are perturbed. We present several equivalent characterizations for the vector equilibrium problem to have nonempty and bounded solution set by using the properties of recession cones. As an application, we show the stability of the solution set for the set-valued vector equilibrium problem in a reflexive Banach space, when both the mapping and the constraint set are perturbed by different parameters. The results presented in this paper extend some corresponding results of Fan and Zhong [39], He [38], Zhong and Huang [40] from the variational inequality to the vector equilibrium problem.
The rest of the paper is organized as follows. In Section 2, we recall some concepts in convex analysis and present some basic results. In Section 3, we present several equivalent characterizations for the set-valued vector equilibrium problems to have nonempty and bounded solution sets. In Section 4, we give an application to the stability of the solution sets for the set-valued vector equilibrium problem.
2. Preliminaries
In this section, we introduce some basic notations and preliminary results.
Let  be a reflexive Banach space and
be a reflexive Banach space and  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . The symbols "
. The symbols " " and "
" and " " are used to denote strong and weak convergence, respectively.
" are used to denote strong and weak convergence, respectively.
The barrier cone of  , denoted by
, denoted by  , is defined by
, is defined by

The recession cone of  , denoted by
, denoted by  , is defined by
, is defined by

It is known that for any given  ,
,

We give some basic properties of recession cones in the following result which will be used in the sequel. Let  be any family of nonempty sets in
be any family of nonempty sets in  . Then
. Then

If, in addition,  and each set
and each set  is closed and convex, then we obtain an equality in the previous inclusion, that is,
is closed and convex, then we obtain an equality in the previous inclusion, that is,

Let  be a proper convex and lower semicontinuous function. The recession function
be a proper convex and lower semicontinuous function. The recession function  of
of  is defined by
is defined by

where  is any point in
is any point in  . Then it follows that
. Then it follows that

The function  turns out to be proper convex, lower semicontinuous and so weakly lower semicontinuous with the property that
turns out to be proper convex, lower semicontinuous and so weakly lower semicontinuous with the property that

Definition 2.1.
A set-valued mapping  is said to be
is said to be
-
(i)
upper semicontinuous at
 if, for any neighborhood
if, for any neighborhood  of
of 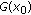 , there exists a neighborhood
, there exists a neighborhood  of
of 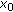 such that
such that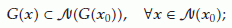 (2.9)
(2.9) -
(ii)
lower semicontinuous at
 if, for any
if, for any 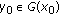 and any neighborhood
and any neighborhood 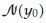 of
of 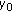 , there exists a neighborhood
, there exists a neighborhood  of
of 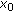 such that
such that (2.10)
(2.10)
We say  is continuous at
is continuous at  if it is both upper and lower semicontinuous at
if it is both upper and lower semicontinuous at  , and we say
, and we say  is continuous on
is continuous on  if it is both upper and lower semicontinuous at every point of
if it is both upper and lower semicontinuous at every point of  .
.
It is evident that  is lower semicontinuous at
is lower semicontinuous at  if and only if, for any sequence
if and only if, for any sequence  with
with  and
and  , there exists a sequence
, there exists a sequence  with
with  such that
such that  .
.
Definition 2.2.
A set-valued mapping  is said to be weakly lower semicontinuous at
is said to be weakly lower semicontinuous at  if, for any
if, for any  and for any sequence
and for any sequence  with
with  , there exists a sequence
, there exists a sequence  such that
such that  .
.
We say  is weakly lower semicontinuous on
is weakly lower semicontinuous on  if it is weakly lower semicontinuous at every point of
if it is weakly lower semicontinuous at every point of  . By Definition 2.2, we know that a weakly lower semicontinuous mapping is lower semicontinuous.
. By Definition 2.2, we know that a weakly lower semicontinuous mapping is lower semicontinuous.
Definition 2.3.
A set-valued mapping  is said to be
is said to be
-
(i)
upper
 -convex on
-convex on 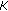 if for any
if for any 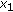 and
and 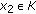 ,
, 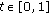 ,
, (2.11)
(2.11) -
(ii)
lower
 -convex on
-convex on 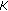 if for any
if for any 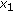 and
and 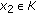 ,
, 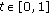 ,
,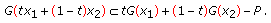 (2.12)
(2.12)
We say that  is
is  -convex if
-convex if  is both upper
is both upper  -convex and lower
-convex and lower  -convex.
-convex.
Definition 2.4.
Let  be a sequence of sets in
be a sequence of sets in  . We define
. We define

Lemma 2.5 (see [36]).
Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  with
with  . Then there exists no sequence
. Then there exists no sequence  such that
such that  and
and  .
.
Lemma 2.6 (see [39]).
Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  with
with  . Then there exists no sequence
. Then there exists no sequence  with each
with each  such that
such that  .
.
Lemma 2.7 (see [39]).
Let  be a metric space and
be a metric space and  be a given point. Let
be a given point. Let  be a set-valued mapping with nonempty values and let
be a set-valued mapping with nonempty values and let  be upper semicontinuous at
be upper semicontinuous at  . Then there exists a neighborhood
. Then there exists a neighborhood  of
of  such that
such that  for all
for all  .
.
Lemma 2.8 (see [41]).
Let  be a nonempty convex subset of a Hausdorff topological vector space
be a nonempty convex subset of a Hausdorff topological vector space  and
and  be a set-valued mapping from
be a set-valued mapping from  into
into  satisfying the following properties:
satisfying the following properties:
-
(i)
 is a KKM mapping, that is, for every finite subset
is a KKM mapping, that is, for every finite subset 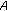 of
of 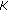 ,
, 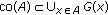 ;
; -
(ii)
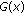 is closed in
is closed in 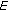 for every
for every  ;
; -
(iii)
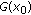 is compact in E for some
is compact in E for some 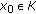 .
.
Then  .
.
3. Boundedness and Nonemptiness of Solution Sets
In this section, we present several equivalent characterizations for the set-valued vector equilibrium problem to have nonempty and bounded solution set. First of all, we give some assumptions which will be used for next theorems.
Let  be a nonempty convex and closed subset of
be a nonempty convex and closed subset of  . Assume that
. Assume that  is a set-valued mapping satisfying the following conditions:
is a set-valued mapping satisfying the following conditions:
( )for each
)for each  ,
,  ;
;
( )for each
)for each  ,
,  implies that
implies that  ;
;
( )for each
)for each  ,
,  is
is  -convex on
-convex on  ;
;
( )for each
)for each  ,
,  is weakly lower semicontinuous on
is weakly lower semicontinuous on  ;
;
( )for each
)for each  , the set
, the set  is closed, here
is closed, here  stands for the closed line segment joining
stands for the closed line segment joining  and
and  .
.
Remark 3.1.
If

where  is a set-valued mapping,
is a set-valued mapping,  is a proper, convex, lower semicontinuous function and
is a proper, convex, lower semicontinuous function and  , then condition
, then condition  reduces to the following
reduces to the following  -pseudomonotonicity assumption which was used in [40]. (See [40, Definition 2.2(iii)] of [40]): for all
-pseudomonotonicity assumption which was used in [40]. (See [40, Definition 2.2(iii)] of [40]): for all  in the graph
in the graph ,
,

Remark 3.2.
If, for each  , the mapping
, the mapping  is lower semicontinuous in
is lower semicontinuous in  , then condition
, then condition  is fulfilled. Indeed, for each
is fulfilled. Indeed, for each  and for any sequence
and for any sequence  with
with  , we have
, we have  and
and  . By the lower semicontinuity of
. By the lower semicontinuity of  , for any
, for any  , there exists
, there exists  such that
such that  . Since
. Since  , we have
, we have  and so
and so  by the closedness of
by the closedness of  . This implies that
. This implies that  and the set
and the set  is closed.
is closed.
The following example shows that conditions  can be satisfied.
can be satisfied.
Example 3.3.
Let  ,
,  ,
,  and
and  . Let
. Let

It is obvious that  holds. Since for each
holds. Since for each  ,
,  and
and  are lower semicontinuous on
are lower semicontinuous on  , by Remark 3.2, we known that conditions
, by Remark 3.2, we known that conditions  and
and  hold. For each
hold. For each  , if
, if  , then we have
, then we have  . This implies that
. This implies that

and so  holds. Moreover, for each
holds. Moreover, for each  ,
,  and
and  with
with  , it is easy to verify that
, it is easy to verify that

which shows that  is
is  -convex on
-convex on  and so
and so  holds. Thus,
holds. Thus,  satisfies all conditions
satisfies all conditions  .
.
Theorem 3.4.
Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  and
and  be a set-valued mapping satisfying assumptions
be a set-valued mapping satisfying assumptions  -
- . Then
. Then  .
.
Proof.
From the assumption  , it is easy to see that
, it is easy to see that  . We now prove that
. We now prove that  . Let
. Let  . Then for all
. Then for all  ,
,  . Set
. Set  , where
, where  . Clearly,
. Clearly,  . From the upper
. From the upper  -convexity of
-convexity of  , we have
, we have

Since  , we obtain
, we obtain

This implies that  and so
and so  . Letting
. Letting  , by assumption
, by assumption  , we have
, we have  . Thus,
. Thus,  and
and  . This completes the proof.
. This completes the proof.
Theorem 3.5.
Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  and
and  be a set-valued mapping satisfying assumptions
be a set-valued mapping satisfying assumptions  . If the solution set
. If the solution set  is nonempty, then
is nonempty, then

Proof.
From the proof of Theorem 3.4, we know that

Let  . Then
. Then  . By the assumptions
. By the assumptions  and
and  , we know that the set
, we know that the set  is nonempty closed and convex. It follows from (2.5) and Theorem 3.4 that
is nonempty closed and convex. It follows from (2.5) and Theorem 3.4 that

Then this completes the proof.
Remark 3.6.
If

where  is a set-valued mapping,
is a set-valued mapping,  is a proper, convex, lower semicontinuous function and
is a proper, convex, lower semicontinuous function and  , then it follows from (3.8) and (2.8) that
, then it follows from (3.8) and (2.8) that

Thus, we know that Theorem 3.5 is a generalization of [40, Theorem 3.1]. Moreover, by [40, Remark 3.1], Theorem 3.5 is also a generalization of [38, Lemma 3.1].
Theorem 3.7.
Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  and
and  be a set-valued mapping satisfying assumptions
be a set-valued mapping satisfying assumptions  . Suppose that
. Suppose that  . Then the following statements are equivalent:
. Then the following statements are equivalent:
-
(i)
the solution set of SVEP
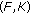 is nonempty and bounded;
is nonempty and bounded; -
(ii)
the solution set of DSVEP
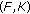 is nonempty and bounded;
is nonempty and bounded; -
(iii)
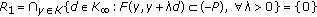 ;
; -
(iv)
there exists a bounded set
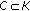 such that for every
such that for every 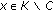 , there exists some
, there exists some  such that
such that 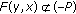 .
.
Proof.
The implications (i) (ii) and (ii)
(ii) and (ii) (iii) follow immediately from Theorems 3.4 and 3.5 and the definition of recession cone.
(iii) follow immediately from Theorems 3.4 and 3.5 and the definition of recession cone.
Now we prove that (iii) implies (iv). If (iv) does not hold, then there exists a sequence  such that for each
such that for each  ,
,  and
and  for every
for every  with
with  . Without loss of generality, we may assume that
. Without loss of generality, we may assume that  weakly converges to
weakly converges to  . Then
. Then  by the definition of the recession cone. Since
by the definition of the recession cone. Since  , by Lemma 2.5, we know that
, by Lemma 2.5, we know that  . Let
. Let  and
and  be any fixed points. For
be any fixed points. For  sufficiently large, by the lower
sufficiently large, by the lower  -convexity of
-convexity of  ,
,

Since

and  is weakly lower semicontinuous, we know that
is weakly lower semicontinuous, we know that  and so
and so  . However, it contradicts the assumption that
. However, it contradicts the assumption that  . Thus (iv) holds.
. Thus (iv) holds.
Since (i) and (ii) are equivalent, it remains to prove that (iv) implies (ii). Let  be a set-valued mapping defined by
be a set-valued mapping defined by

We first prove that  is a closed subset of
is a closed subset of  . Indeed, for any
. Indeed, for any  with
with  , we have
, we have  . It follows from the weakly lower semicontinuity of
. It follows from the weakly lower semicontinuity of  that
that  . This shows that
. This shows that  and so
and so  is closed.
is closed.
We next prove that  is a KKM mapping from
is a KKM mapping from  to
to  . Suppose to the contrary that there exist
. Suppose to the contrary that there exist  with
with  ,
,  and
and  such that
such that  . Then
. Then

By assumption  , we have
, we have

It follows from the upper  -convexity of
-convexity of  that
that

which is a contradiction with (3.17). Thus we know that  is a KKM mapping.
is a KKM mapping.
We may assume that  is a bounded closed convex set (otherwise, consider the closed convex hull of
is a bounded closed convex set (otherwise, consider the closed convex hull of  instead of
instead of  ). Let
). Let  be finite number of points in
be finite number of points in  and let
and let  . Then the reflexivity of the space
. Then the reflexivity of the space  yields that
yields that  is weakly compact convex. Consider the set-valued mapping
is weakly compact convex. Consider the set-valued mapping  defined by
defined by  for all
for all  . Then each
. Then each  is a weakly compact convex subset of
is a weakly compact convex subset of  and
and  is a KKM mapping. We claim that
is a KKM mapping. We claim that

Indeed, by Lemma 2.8, intersection in (3.19) is nonempty. Moreover, if there exists some  but
but  , then by (iv), we have
, then by (iv), we have  for some
for some  . Thus,
. Thus,  and so
and so  , which is a contradiction to the choice of
, which is a contradiction to the choice of  .
.
Let  . Then
. Then  by (3.19) and so
by (3.19) and so  . This shows that the collection
. This shows that the collection  has finite intersection property. For each
has finite intersection property. For each  , it follows from the weak compactness of
, it follows from the weak compactness of  that
that  is nonempty, which coincides with the solution set of DSVEP
is nonempty, which coincides with the solution set of DSVEP .
.
Remark 3.8.
Theorem 3.7 establishes the necessary and sufficient conditions for the vector equilibrium problem to have nonempty and bounded solution sets. If

where  is a set-valued mapping,
is a set-valued mapping,  is a proper, convex, lower semicontinuous function and
is a proper, convex, lower semicontinuous function and  , then problem (1.2) reduces to the following Minty mixed variational inequality: finding
, then problem (1.2) reduces to the following Minty mixed variational inequality: finding  such that
such that

which was considered by Zhong and Huang [40]. Therefore, Theorem 3.7 is a generalization of [40, Theorem 3.2]. Moreover, by [40, Remark 3.2], Theorem 3.7 is also a generalization of Theorem 3.4 due to He [38].
Remark 3.9.
By using a asymptotic analysis methods, many authors studied the necessary and sufficient conditions for the nonemptiness and boundedness of the solution sets to variational inequalities, optimization problems, and equilibrium problems, we refer the reader to references [42–49] for more details.
4. An Application
As an application, in this section, we will establish the stability of solution set for the set-valued vector equilibrium problem when the mapping and the constraint set are perturbed by different parameters.
Let  and
and  be two metric spaces.
be two metric spaces.  is a set-valued mapping satisfying the following assumptions:
is a set-valued mapping satisfying the following assumptions:
( )for each
)for each  ,
,  ,
,  ,
,  ;
;
( )for each
)for each  ,
,  ,
,  ,
,  implies that
implies that  ;
;
( )for each
)for each  ,
,  ,
,  ,
,  is
is  -convex on
-convex on  ;
;
( )for each
)for each  ,
,  and
and  , for any sequences
, for any sequences  ,
,  and
and  with
with  ,
,  and
and  , there exists a sequence
, there exists a sequence  with
with  such that
such that  .
.
The following Theorem 4.1 plays an important role in proving our results.
Theorem 4.1.
Let  and
and  be two metric spaces,
be two metric spaces,  and
and  be given points. Let
be given points. Let  be a continuous set-valued mapping with nonempty closed convex values and
be a continuous set-valued mapping with nonempty closed convex values and  . Suppose that
. Suppose that  is a set-valued mapping satisfying the assumptions
is a set-valued mapping satisfying the assumptions  . If
. If

then there exists a neighborhood  of
of  such that
such that

Proof.
Assume that the conclusion does not hold, then there exist a sequence  in
in  with
with  such that
such that  .
.
Since  is cone, we can select a sequence
is cone, we can select a sequence  with
with  such that
such that  for every
for every  . As
. As  is reflexive, without loss of generality, we can assume that
is reflexive, without loss of generality, we can assume that  , as
, as  . Since
. Since  is a continuous set-valued mapping, hence,
is a continuous set-valued mapping, hence,  is upper semicontinuous and lower semicontinuous at
is upper semicontinuous and lower semicontinuous at  . From the upper semicontinuity of
. From the upper semicontinuity of  , by Lemma 2.7, we have
, by Lemma 2.7, we have  as
as  large enough and hence
large enough and hence  as
as  large enough. Since
large enough. Since  is a closed convex cone and hence weakly closed. This implies that
is a closed convex cone and hence weakly closed. This implies that  . Moreover, it follows from Lemma 2.6 that
. Moreover, it follows from Lemma 2.6 that  .
.
For any  ,
,  and
and  , from the lower semicontinuity of
, from the lower semicontinuity of  , there exists
, there exists  such that
such that  . Since
. Since  , it follows that
, it follows that  . Together with
. Together with  , from assumption
, from assumption  , there exists
, there exists  such that
such that  . Since
. Since  , we have
, we have  and
and  . Letting
. Letting  , we obtain that
, we obtain that  . Since
. Since  and
and  are arbitrary, from the above discussion, we obtain
are arbitrary, from the above discussion, we obtain  with
with  . This contradicts our assumption that
. This contradicts our assumption that  . This completes the proof.
. This completes the proof.
Remark 4.2.
If

where  is a set-valued mapping,
is a set-valued mapping,  is a proper, convex, lower semicontinuous function and
is a proper, convex, lower semicontinuous function and  , from Remark 3.6, we know that (4.1) and (4.2) in Theorem 4.1 reduce to (4.1) and (4.2) in [40, Theorem 4.1], respectively. Therefore, Theorem 4.1 is a generalization of [40, Theorem 4.1]. Moreover, by [40, Remark 4.1], Theorem 4.1 is also a generalization of [39, Theorem 3.1].
, from Remark 3.6, we know that (4.1) and (4.2) in Theorem 4.1 reduce to (4.1) and (4.2) in [40, Theorem 4.1], respectively. Therefore, Theorem 4.1 is a generalization of [40, Theorem 4.1]. Moreover, by [40, Remark 4.1], Theorem 4.1 is also a generalization of [39, Theorem 3.1].
From Theorem 4.1, we derive the following stability result of the solution set for the vector equilibrium problem.
Theorem 4.3.
Let  and
and  be two metric spaces,
be two metric spaces,  and
and  be given points. Let
be given points. Let  be a continuous set-valued mapping with nonempty closed convex values and
be a continuous set-valued mapping with nonempty closed convex values and  . Suppose that
. Suppose that  is a set-valued mapping satisfying the assumptions
is a set-valued mapping satisfying the assumptions  -
- . If
. If  is nonempty and bounded, then
is nonempty and bounded, then
-
(i)
there exists a neighborhood
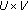 of
of 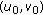 such that for every
such that for every  ,
, 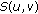 is nonempty and bounded;
is nonempty and bounded; -
(ii)
 -
- .
.
Proof.
If  is nonempty and bounded, then by Theorem 3.7 we have
is nonempty and bounded, then by Theorem 3.7 we have  . It follows from Theorem 4.1 that there exists a neighborhood
. It follows from Theorem 4.1 that there exists a neighborhood  of
of  , such that
, such that  for every
for every  . By using Theorem 3.7 again, we have
. By using Theorem 3.7 again, we have  is nonempty and bounded for every
is nonempty and bounded for every  . This verifies the first assertion.
. This verifies the first assertion.
Next, we prove the second assertion  -
- . For any given sequence
. For any given sequence  with
with  , we need to prove that
, we need to prove that  -
- . Let
. Let  -
- . Then there exists a sequence
. Then there exists a sequence  with each
with each  such that
such that  weakly converges to
weakly converges to  . We claim that there exists
. We claim that there exists  such that
such that  . Indeed, if the claim does hold, then there exist that a subsequence
. Indeed, if the claim does hold, then there exist that a subsequence  of
of  and some
and some  , such that
, such that  , for all
, for all  . This implies that
. This implies that  and so
and so  , which contradicts with the upper semicontinuity of
, which contradicts with the upper semicontinuity of  . Thus, we have the claim. Moreover, we obtain
. Thus, we have the claim. Moreover, we obtain  as
as  is a closed convex subset of
is a closed convex subset of  and hence weakly closed.
and hence weakly closed.
Now we prove  for all
for all  and hence
and hence  . For any
. For any  and
and  , from the lower semicontinuity of
, from the lower semicontinuity of  , there exist
, there exist  such that
such that  . Moreover, from assumption
. Moreover, from assumption  , there exists a sequence of elements
, there exists a sequence of elements  such that
such that  . Since
. Since  , we have
, we have  and so
and so  . Letting
. Letting  , we obtain that
, we obtain that  . Since
. Since  is arbitrary, we have
is arbitrary, we have  . This yields that
. This yields that  . Thus, have the second assertion. This completes the proof.
. Thus, have the second assertion. This completes the proof.
Remark 4.4.
If

where  is a set-valued mapping,
is a set-valued mapping,  is a proper, convex, lower semicontinuous function and
is a proper, convex, lower semicontinuous function and  , then problem (1.4) reduces to the following parametric Minty mixed variational inequality: finding
, then problem (1.4) reduces to the following parametric Minty mixed variational inequality: finding  such that
such that

which was considered by Zhong and Huang [40]. Therefore, Theorem 4.3 is a generalization of [40, Theorem 4.2]. Moreover, by [40, Remark 4.2], Theorem 4.3 ia also a generalizationof Theorems 4.1 and 4.4 due to He [38] and Theorem 3.5 due to Fan and Zhong [39].
The following examples show the necessity of the conditions of Theorem 4.3.
Example 4.5.
Let  ,
,  ,
,  and
and  ,
,

Note that  is continuous on
is continuous on  . However,
. However,  is not lower semicontinuous at
is not lower semicontinuous at  . Clearly, we have
. Clearly, we have  and
and  for any
for any  . Thus,
. Thus,

Example 4.6.
Let  ,
,  ,
,  and
and  ,
,

Note that  satisfies the assumptions
satisfies the assumptions  , and
, and  is upper semicontinuous. However,
is upper semicontinuous. However,  is not lower semicontinuous at
is not lower semicontinuous at  . Clearly, we have
. Clearly, we have  and
and  for any
for any  . Thus,
. Thus,

Example 4.7.
Let  ,
,  ,
,  ,
,  ,
,

Note that  satisfies the assumptions
satisfies the assumptions  and
and  is lower semicontinuous. However,
is lower semicontinuous. However,  is not upper semicontinuous at
is not upper semicontinuous at  . Clearly, we have
. Clearly, we have  and
and  for any
for any  . Thus,
. Thus,

References
Giannessi F: Theorems of alternative, quadratic programs and complementarity problems. In Variational Inequalities and Complementarity Problems. Edited by: Cottle RW, Giannessi F, Lions JL. John Wiley & Sons, Chichester, UK; 1980:151–186.
Giannessi F (Ed): Vector Variational Inequalities and Vector Equilibrium. Volume 38. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2000:xiv+523.
Blum E, Oettli W: From optimization and variational inequalities to equilibrium problems. The Mathematics Student 1994,63(1–4):123–145.
Chen G, Huang X, Yang X: Vector Optimization: Set-Valued and Variational Analysis, Lecture Notes in Economics and Mathematical Systems. Volume 541. Springer, Berlin, Germany; 2005:x+306.
Chen GY, Yang XQ, Yu H: A nonlinear scalarization function and generalized quasi-vector equilibrium problems. Journal of Global Optimization 2005,32(4):451–466. 10.1007/s10898-003-2683-2
Huang N-J, Fang Y-P: Strong vector F -complementary problem and least element problem of feasible set. Nonlinear Analysis. Theory, Methods & Applications 2005,61(6):901–918. 10.1016/j.na.2005.01.021
Huang NJ, Fang YP: On vector variational inequalities in reflexive Banach spaces. Journal of Global Optimization 2005,32(4):495–505. 10.1007/s10898-003-2686-z
Tan KK, Yu J, Yuan XZ: Existence theorems for saddle points of vector-valued maps. Journal of Optimization Theory and Applications 1996,89(3):731–747. 10.1007/BF02275357
Yang XQ: Vector complementarity and minimal element problems. Journal of Optimization Theory and Applications 1993,77(3):483–495. 10.1007/BF00940446
Ansari QH, Chan WK, Yang XQ: The system of vector quasi-equilibrium problems with applications. Journal of Global Optimization 2004,29(1):45–57.
Ansari QH, Oettli W, Schläger D: A generalization of vectorial equilibria. Mathematical Methods of Operations Research 1997,46(2):147–152. 10.1007/BF01217687
Ansari QH, Schaible S, Yao JC: System of vector equilibrium problems and its applications. Journal of Optimization Theory and Applications 2000,107(3):547–557. 10.1023/A:1026495115191
Ansari QH, Yao J-C: An existence result for the generalized vector equilibrium problem. Applied Mathematics Letters 1999,12(8):53–56. 10.1016/S0893-9659(99)00121-4
Bianchi M, Schaible S: Generalized monotone bifunctions and equilibrium problems. Journal of Optimization Theory and Applications 1996,90(1):31–43. 10.1007/BF02192244
Bianchi M, Hadjisavvas N, Schaible S: Vector equilibrium problems with generalized monotone bifunctions. Journal of Optimization Theory and Applications 1997,92(3):527–542. 10.1023/A:1022603406244
Fang Y-P, Huang N-J, Kim JK: Existence results for systems of vector equilibrium problems. Journal of Global Optimization 2006,35(1):71–83. 10.1007/s10898-005-1654-1
Fu J-Y: Symmetric vector quasi-equilibrium problems. Journal of Mathematical Analysis and Applications 2003,285(2):708–713. 10.1016/S0022-247X(03)00479-7
Gong X: Strong vector equilibrium problems. Journal of Global Optimization 2006,36(3):339–349. 10.1007/s10898-006-9012-5
Huang NJ, Li J, Thompson HB: Implicit vector equilibrium problems with applications. Mathematical and Computer Modelling 2003,37(12–13):1343–1356. 10.1016/S0895-7177(03)90045-8
Huang NJ, Li J, Wu S-Y: Gap functions for a system of generalized vector quasi-equilibrium problems with set-valued mappings. Journal of Global Optimization 2008,41(3):401–415. 10.1007/s10898-007-9248-8
Huang NJ, Li J, Yao JC: Gap functions and existence of solutions for a system of vector equilibrium problems. Journal of Optimization Theory and Applications 2007,133(2):201–212. 10.1007/s10957-007-9202-4
Konnov IV, Yao JC: Existence of solutions for generalized vector equilibrium problems. Journal of Mathematical Analysis and Applications 1999,233(1):328–335. 10.1006/jmaa.1999.6312
Lin L-J: System of generalized vector quasi-equilibrium problems with applications to fixed point theorems for a family of nonexpansive multivalued mappings. Journal of Global Optimization 2006,34(1):15–32. 10.1007/s10898-005-4702-y
Lin LJ, Hsu HW: Existence theorems for systems of generalized vector quasiequilibrium problems and optimization problems. Journal of Global Optimization 2007, 37: 195–213. 10.1007/s10898-006-9044-x
Li J, Huang NJ, Kim JK: On implicit vector equilibrium problems. Journal of Mathematical Analysis and Applications 2003,283(2):501–512. 10.1016/S0022-247X(03)00277-4
Li SJ, Teo KL, Yang XQ: Generalized vector quasi-equilibrium problems. Mathematical Methods of Operations Research 2005,61(3):385–397. 10.1007/s001860400412
Anh LQ, Khanh PQ: On the stability of the solution sets of general multivalued vector quasiequilibrium problems. Journal of Optimization Theory and Applications 2007,135(2):271–284. 10.1007/s10957-007-9250-9
Anh LQ, Khanh PQ: Semicontinuity of solution sets to parametric quasivariational inclusions with applications to traffic networks—II. Lower semicontinuities applications. Set-Valued Analysis 2008,16(7–8):943–960. 10.1007/s11228-008-0082-z
Chen JC, Gong XH: The stability of set of solutions for symmetric vector quasi-equilibrium problems. Journal of Optimization Theory and Applications 2008,136(3):359–374. 10.1007/s10957-007-9309-7
Gong XH: Continuity of the solution set to parametric weak vector equilibrium problems. Journal of Optimization Theory and Applications 2008,139(1):35–46. 10.1007/s10957-008-9429-8
Gong XH, Yao JC: Lower semicontinuity of the set of efficient solutions for generalized systems. Journal of Optimization Theory and Applications 2008,138(2):197–205. 10.1007/s10957-008-9379-1
Huang NJ, Li J, Thompson HB: Stability for parametric implicit vector equilibrium problems. Mathematical and Computer Modelling 2006,43(11–12):1267–1274. 10.1016/j.mcm.2005.06.010
Long X-J, Huang NJ, Teo K-l: Existence and stability of solutions for generalized strong vector quasi-equilibrium problem. Mathematical and Computer Modelling 2008,47(3–4):445–451. 10.1016/j.mcm.2007.04.013
McLinden L: Stable monotone variational inequalities. Mathematical Programming 1990,48(2):303–338.
Adly S: Stability of linear semi-coercive variational inequalities in Hilbert spaces: application to the Signorini-Fichera problem. Journal of Nonlinear and Convex Analysis 2006,7(3):325–334.
Adly S, Théra M, Ernst E: Stability of the solution set of non-coercive variational inequalities. Communications in Contemporary Mathematics 2002,4(1):145–160. 10.1142/S0219199702000579
Addi K, Adly S, Goeleven D, Saoud H: A sensitivity analysis of a class of semi-coercive variational inequalities using recession tools. Journal of Global Optimization 2008,40(1–3):7–27.
He Y: Stable pseudomonotone variational inequality in reflexive Banach spaces. Journal of Mathematical Analysis and Applications 2007,330(1):352–363. 10.1016/j.jmaa.2006.07.063
Fan JH, Zhong RY: Stability analysis for variational inequality in reflexive Banach spaces. Nonlinear Analysis. Theory, Methods & Applications 2008,69(8):2566–2574. 10.1016/j.na.2007.08.031
Zhong R, Huang N: Stability analysis for minty mixed variational inequality in reflexive Banach spaces. Journal of Optimization Theory and Applications 2010,147(3):454–472. 10.1007/s10957-010-9732-z
Fan K: A generalization of Tychonoff's fixed point theorem. Mathematische Annalen 1961, 142: 305–310. 10.1007/BF01353421
Ansari QH, Flores-Bazán F: Recession methods for generalized vector equilibrium problems. Journal of Mathematical Analysis and Applications 2006,321(1):132–146. 10.1016/j.jmaa.2005.07.059
Daniilidis A, Hadjisavvas N: Coercivity conditions and variational inequalities. Mathematical Programming 1999,86(2):433–438. 10.1007/s101070050097
Deng S: Boundedness and nonemptiness of the efficient solution sets in multiobjective optimization. Journal of Optimization Theory and Applications 2010,144(1):29–42. 10.1007/s10957-009-9589-1
Deng S: Characterizations of the nonemptiness and boundedness of weakly efficient solution sets of convex vector optimization problems in real reflexive Banach spaces. Journal of Optimization Theory and Applications 2009,140(1):1–7. 10.1007/s10957-008-9443-x
Flores-Bazán F: Existence theorems for generalized noncoercive equilibrium problems: the quasi-convex case. SIAM Journal on Optimization 2000,11(3):675–690.
Flores-Bazán F: Vector equilibrium problems under asymptotic analysis. Journal of Global Optimization 2003,26(2):141–166. 10.1023/A:1023048928834
Flores-Bazán F, Vera C: Characterization of the nonemptiness and compactness of solution sets in convex and nonconvex vector optimization. Journal of Optimization Theory and Applications 2006,130(2):185–207. 10.1007/s10957-006-9098-4
Huang XX, Yang XQ, Teo KL: Characterizing nonemptiness and compactness of the solution set of a convex vector optimization problem with cone constraints and applications. Journal of Optimization Theory and Applications 2004,123(2):391–407. 10.1007/s10957-004-5155-z
Acknowledgments
The authors are grateful to the editor and reviewers for their valuable comments and suggestions. This work was supported by the Key Program of NSFC (Grant no. 70831005), the National Natural Science Foundation of China (10671135) and the Korea Research Foundation Grant funded by the Korean Government (KRF-2008-313-C00050).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhong, RY., Huang, NJ. & Cho, Y. Boundedness and Nonemptiness of Solution Sets for Set-Valued Vector Equilibrium Problems with an Application. J Inequal Appl 2011, 936428 (2011). https://doi.org/10.1155/2011/936428
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/936428
 if, for any neighborhood
if, for any neighborhood  of
of 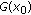 , there exists a neighborhood
, there exists a neighborhood  of
of 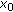 such that
such that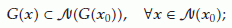
 if, for any
if, for any 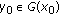 and any neighborhood
and any neighborhood 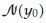 of
of 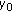 , there exists a neighborhood
, there exists a neighborhood  of
of 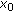 such that
such that
 -convex on
-convex on 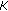 if for any
if for any 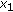 and
and 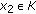 ,
, 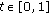 ,
,
 -convex on
-convex on 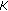 if for any
if for any 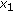 and
and 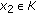 ,
, 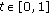 ,
,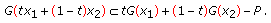
 is a KKM mapping, that is, for every finite subset
is a KKM mapping, that is, for every finite subset 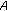 of
of 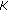 ,
, 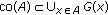 ;
;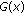 is closed in
is closed in 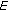 for every
for every  ;
;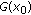 is compact in E for some
is compact in E for some 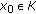 .
.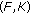 is nonempty and bounded;
is nonempty and bounded;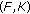 is nonempty and bounded;
is nonempty and bounded;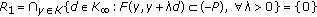 ;
;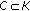 such that for every
such that for every 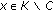 , there exists some
, there exists some  such that
such that 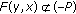 .
.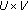 of
of 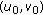 such that for every
such that for every  ,
, 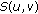 is nonempty and bounded;
is nonempty and bounded; -
- .
.