- Research Article
- Open access
- Published:
Nonsquareness and Locally Uniform Nonsquareness in Orlicz-Bochner Function Spaces Endowed with Luxemburg Norm
Journal of Inequalities and Applications volume 2011, Article number: 875649 (2011)
Abstract
Criteria for nonsquareness and locally uniform nonsquareness of Orlicz-Bochner function spaces equipped with Luxemburg norm are given. We also prove that, in Orlicz-Bochner function spaces generated by locally uniform nonsquare Banach space, nonsquareness and locally uniform nonsquareness are equivalent.
1. Introduction
A lot of nonsquareness concepts in Banach spaces are known (see [1]). Nonsquareness are important notions in geometry of Banach space. One of reasons is that these properties are strongly related to the fixed point property (see [2]). The criteria for nonsquareness and locally uniform nonsquareness in the classical Orlicz function spaces have been given in [3, 4] already. However, because of the complicated structure of Orlicz-Bochner function spaces equipped with the Luxemburg norm, the criteria for nonsquareness and locally uniform nonsquareness of them have not been found yet. The aim of this paper is to give criteria for nonsquareness and locally uniform nonsquareness of Orlicz-Bochner function spaces equipped with Luxemburg norm.
Let  be a real Banach space.
be a real Banach space.  and
and  denote the unit sphere and unit ball, respectively. Let us recall some geometrical notions concerning nonsquareness. A Banach space
denote the unit sphere and unit ball, respectively. Let us recall some geometrical notions concerning nonsquareness. A Banach space  is said to be nonsquare if for any
is said to be nonsquare if for any  we have
we have  . A Banach space
. A Banach space  is said to be uniformly nonsquare if there exists
is said to be uniformly nonsquare if there exists  such that for any
such that for any  ,
,  . A Banach space
. A Banach space  is said to be locally uniformly nonsquare if for any
is said to be locally uniformly nonsquare if for any  , there exists
, there exists  such that
such that  , where
, where  .
.
Let  be set of real numbers. A function
be set of real numbers. A function  is called an
is called an  -function if
-function if  is convex, even,
is convex, even,  ,
,  and
and  , and
, and  .
.
Let  be a nonatomic measurable space.
be a nonatomic measurable space.  denotes right derivative of
denotes right derivative of  . Moreover, for a given Banach space
. Moreover, for a given Banach space  , we denote by
, we denote by  the set of all strongly
the set of all strongly  -measurable function from
-measurable function from  to
to  , and for each
, and for each  , we define the modular of
, we define the modular of  by
by

Put

The linear set  endowed with the Luxemburg norm
endowed with the Luxemburg norm

is a Banach space. We say that an Orlicz function  satisfies condition
satisfies condition  if there exist
if there exist  and
and  such that
such that

First let us recall a known result that will be used in the further part of the paper.
Lemma 1.1 (see [3]).
Suppose  . Then
. Then

2. Main Results
Theorem 2.1.
 is nonsquare if and only if
is nonsquare if and only if
(a) ;
;
(b) is nonsquare.
is nonsquare.
In order to prove the theorem, we give a lemma.
Lemma 2.2.
If  is nonsquare, then for any
is nonsquare, then for any  , we have
, we have

Proof.
Case 1.
If  , then
, then

or

Case 2.
If  , then
, then

or

This implies  . This completes the proof.
. This completes the proof.
Proof of Theorem 2.1.
-
(a)
Necessity. Suppose that
 , then there exist
, then there exist 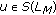 and
and  such that
such that 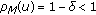 . Pick
. Pick  such that
such that 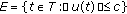 is not a null set. Since
is not a null set. Since  , there exist sequence
, there exist sequence 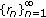 and disjont subsets
and disjont subsets 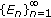 of
of 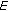 such that
such that 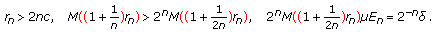 (2.6)
(2.6)
Therefore, if we define  , then for any
, then for any  , we have
, we have

This yields

Hence,  . But
. But  , and we deduce that
, and we deduce that  . Moreover, we have
. Moreover, we have  and
and  , a contradiction with nonsquareness of
, a contradiction with nonsquareness of  .
.
If (b) is not true, then there exist  such that
such that  . Pick
. Pick  such that
such that  . Put
. Put

Then we have

It is easy to see  . We know that
. We know that

Hence, we have

It is easy to see  , a contradiction!
, a contradiction!
Sufficiency. Suppose that there exists  such that
such that

We will derive a contradiction for each of the following two cases.
Case 1.
 . Let
. Let  . Hence, we have
. Hence, we have

Since  , we have
, we have  . Hence,
. Hence,  . This implies
. This implies  , a contradiction!
, a contradiction!
Case 2.
 . By Lemma 2.2, without loss of generality, we may assume that there exists
. By Lemma 2.2, without loss of generality, we may assume that there exists  such that
such that  ,
,  and
and  . Therefore,
. Therefore,

Since  , we have
, we have  . Hence,
. Hence,  . This implies
. This implies  , a contradiction!
, a contradiction!
Theorem 2.3.
 is locally uniformly nonsquare if and only if
is locally uniformly nonsquare if and only if
(a) ;
;
(b) is locally uniformly nonsquare.
is locally uniformly nonsquare.
In order to prove the theorem, we give a lemma.
Lemma 2.4.
If  is locally uniformly nonsquare, then
is locally uniformly nonsquare, then
(a)For any  ,
,  , we have
, we have

(b)If  , then
, then  , where
, where

Proof.
-
(a)
Since
 is locally uniformly nonsquare, we have
is locally uniformly nonsquare, we have 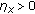 and
and 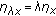 , where
, where 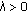 and
and  (2.18)
(2.18)
In fact, since  is locally uniformly nonsquare, we have
is locally uniformly nonsquare, we have

Case 1.
If  , then
, then

or

Case 2.
If  , then
, then

or

Therefore, we get, the following inequality

holds.
(b1) Suppose that  , where
, where  . Then there exist
. Then there exist  and subsequence
and subsequence  of
of  , such that
, such that  . By definition of
. By definition of  , there exist
, there exist  such that
such that

We will derive a contradiction for each of the following two cases.
Case 1.
 . Since
. Since  , there exists
, there exists  such that
such that  . Therefore,
. Therefore,

This implies  , a contradiction!
, a contradiction!
Case 2.
 . Without loss of generality, we may assume
. Without loss of generality, we may assume  , where
, where  . Since
. Since  , there exists
, there exists  such that
such that  . Therefore, we have
. Therefore, we have

This implies

Similarly, we have

Therefore, we have

This implies  , a contradiction! Hence,
, a contradiction! Hence,  .
.
(b2) Suppose that  , where
, where  . Then there exist
. Then there exist  and subsequence
and subsequence  of
of  , such that
, such that  . Since
. Since  , then there exist
, then there exist  such that
such that  , whenever
, whenever  . By definition of
. By definition of  , there exist
, there exist  such that
such that

Therefore, we have

whenever  . Since
. Since  , there exists
, there exists  such that
such that  , where
, where

Hence, we have

This implies

which contradict (2.32). Hence,  .
.
Combing (b1) with (b2), we get  . This completes the proof.
. This completes the proof.
Proof of Theorem 2.3.
Necessity. By Theorem 2.1,  . If (b) is not true, then there exist
. If (b) is not true, then there exist  ,
,  such that
such that  and
and  as
as  . Pick
. Pick  such that
such that  . Put
. Put

Then we have

It is easy to see  . We know that
. We know that

Moreover, we have  ,
,  . By the dominated convergence theorem, we have
. By the dominated convergence theorem, we have

It is easy to see  ,
,  as
as  . By Lemma 1.1, we have
. By Lemma 1.1, we have  and
and  as
as  , a contradiction with locally uniform nonsquareness of
, a contradiction with locally uniform nonsquareness of  .
.
Sufficiency. Suppose that there exist  ,
,  such that
such that  as
as  . We will derive a contradiction for each of the following two cases.
. We will derive a contradiction for each of the following two cases.
Case 1.
There exist  ,
,  such that
such that  , where
, where  . Put
. Put

We have

This implies  . Hence,
. Hence,  . We define a function
. We define a function

on  , where
, where  . By Lemma 2.4, we have
. By Lemma 2.4, we have  -a.e on
-a.e on  . Let
. Let  -a.e on
-a.e on  , where
, where  is simple function. Hence,
is simple function. Hence,

is  -measurable. By Lemma 2.4, we have
-measurable. By Lemma 2.4, we have  -a.e on
-a.e on  . Then
. Then  is
is  -measurable. Using
-measurable. Using

we get that there exists  such that
such that  , where
, where

Let  ,
,  ,
,  . It is easy to see
. It is easy to see  ,
,  and
and  . If
. If  , by Lemma 2.4, we have
, by Lemma 2.4, we have

Without loss of generality, we may assume that there exists  such that
such that

Moreover, for any  , we have
, we have

Hence, if  , then
, then

Let  . Then
. Then  . Therefore,
. Therefore,

By Lemma 1.1, we have  ,
,  as
as  . This is in contradiction with
. This is in contradiction with  .
.
Case 2.
For any  ,
,  , there exists
, there exists  such that
such that  whenever
whenever  . By the Riesz theorem, without loss of generality, we may assume that
. By the Riesz theorem, without loss of generality, we may assume that  a.e on
a.e on  . Using
. Using

we get that there exist  such that
such that  , where
, where

Since  is
is  -function, we can choose
-function, we can choose  such that
such that 
 . Since
. Since 
 a.e on
a.e on  , by the Egorov theorem, there exists
, by the Egorov theorem, there exists  such that
such that  whenever
whenever  , where
, where  ,
,  . Next, we will prove that if
. Next, we will prove that if  , then
, then

In fact, we have

Moreover, we have

By (2.54) and (2.55), we have

This shows that if  , then
, then

It is easy to see  . Therefore,
. Therefore,

for  large enough. By Lemma 1.1, we have
large enough. By Lemma 1.1, we have  ,
, 
 as
as  , which contradicts
, which contradicts  , for
, for  large enough. This completes the proof.
large enough. This completes the proof.
Corollary 2.5.
The following statements are equivalent:
(a) is locally uniformly nonsquare if and only if
is locally uniformly nonsquare if and only if  is nonsquare;
is nonsquare;
(b) is locally uniformly nonsquare.
is locally uniformly nonsquare.
References
James RC: Uniform nonsquare Banach space. Annals of Mathematics 1964,80(3):542–550. 10.2307/1970663
García-Falset J, Llorens-Fuster E, Mazcuñan-Navarro EM: Uniformly nonsquare Banach spaces have the fixed point property for nonexpansive mappings. Journal of Functional Analysis 2006,233(2):494–514. 10.1016/j.jfa.2005.09.002
Chen ST: Geometry of Orlicz spaces. Dissertationes Math 1996, 356: 1–204.
Wu CX, Wang TF, Chen ST, Wang YW: Geometry Theory of Orlicz Spaces. H.I.T Print House, Harbin, China; 1986.
Acknowledgments
The authors would like to thank the anonymous referee for some suggestions to improve the manuscript. This work was supported by China Natural Science Fund under Grant no. 11061022.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Shang, S., Cui, Y. & Fu, Y. Nonsquareness and Locally Uniform Nonsquareness in Orlicz-Bochner Function Spaces Endowed with Luxemburg Norm. J Inequal Appl 2011, 875649 (2011). https://doi.org/10.1155/2011/875649
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/875649
 , then there exist
, then there exist 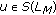 and
and  such that
such that 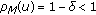 . Pick
. Pick  such that
such that 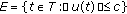 is not a null set. Since
is not a null set. Since  , there exist sequence
, there exist sequence 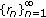 and disjont subsets
and disjont subsets 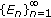 of
of 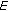 such that
such that 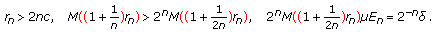
 is locally uniformly nonsquare, we have
is locally uniformly nonsquare, we have 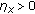 and
and 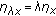 , where
, where 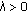 and
and 