- Research Article
- Open access
- Published:
Normality Criteria of Lahiri's Type and Their Applications
Journal of Inequalities and Applications volume 2011, Article number: 873184 (2011)
Abstract
We prove two normality criteria for families of some functions concerning Lahiri's type, the results generalize those given by Charak and Rieppo, Xu and Cao. As applications, we study a problem related to R. Brück's Conjecture and obtain a result that generalizes those given by Yang and Zhang, Lü, Xu and Chen.
1. Introduction and Main Results
Let  denote the complex plane, and let
denote the complex plane, and let  be a nonconstant meromorphic function in
be a nonconstant meromorphic function in  . It is assumed that the reader is familiar with the standard notion used in the Nevanlinna value distribution theory such as the characteristic function
. It is assumed that the reader is familiar with the standard notion used in the Nevanlinna value distribution theory such as the characteristic function  , the proximity function
, the proximity function  , the counting function
, the counting function  (see, e.g., [1–4]), and
(see, e.g., [1–4]), and  denotes any quantity that satisfies the condition
denotes any quantity that satisfies the condition  as
as  outside of a possible exceptional set of finite linear measure. A meromorphic function
outside of a possible exceptional set of finite linear measure. A meromorphic function  is called a small function with respect to
is called a small function with respect to  , provided that
, provided that  .
.
Let  and
and  be two nonconstant meromorphic functions. Let
be two nonconstant meromorphic functions. Let  and
and  be small functions of
be small functions of  and
and  .
.  means
means  and
and  have the same zeros (counting multiplicity) and
have the same zeros (counting multiplicity) and  means that
means that  and
and  have the same poles (counting multiplicity). If
have the same poles (counting multiplicity). If  whenever
whenever  , we write
, we write  . If
. If  and
and  , we write
, we write  . If
. If  , then we say that
, then we say that  and
and  share
share  .
.
Set

where  ,
,  are nonnegative integers.
are nonnegative integers.  is called the differential monomial of
is called the differential monomial of  and
and  is called the degree of
is called the degree of  .
.
Let  be a family of meromorphic functions defined in a domain
be a family of meromorphic functions defined in a domain  .
.  is said to be normal in
is said to be normal in  , in the sense of Montel, if for any sequence
, in the sense of Montel, if for any sequence  , there exists a subsequence
, there exists a subsequence  such that
such that  converges spherically locally uniformly in
converges spherically locally uniformly in  , to a meromorphic function or
, to a meromorphic function or  .
.
According to Bloch's principle, every condition which reduces a meromorphic function in  to a constant makes a family of meromorphic functions in a domain
to a constant makes a family of meromorphic functions in a domain  normal. Although the principle is false in general, many authors proved normality criteria for families of meromorphic functions starting from Picard type theorems, for instance.
normal. Although the principle is false in general, many authors proved normality criteria for families of meromorphic functions starting from Picard type theorems, for instance.
Theorem A (see [5]).
Let  be an integer,
be an integer,  and
and  . If, for a meromorphic function
. If, for a meromorphic function  ,
,  for all
for all  , then
, then  must be a constant.
must be a constant.
Let  be an integer,
be an integer,  ,
,  , and let
, and let  , be a family of meromorphic functions in a domain
, be a family of meromorphic functions in a domain  . If
. If  for all
for all  , then
, then  is a normal family.
is a normal family.
In 2005, Lahiri [8] got a normality criterion as follows.
Theorem C.
Let  be a family of meromorphic functions in a complex domain
be a family of meromorphic functions in a complex domain  . Let
. Let  such that
such that  . Define
. Define

If there exists a positive constant  such that
such that  for all
for all  whenever
whenever  , then
, then  is a normal family.
is a normal family.
In 2009, Charak and Rieppo [9] generalized Theorem C and obtained two normality criteria of Lahiri's type.
Theorem D.
Let  be a family of meromorphic functions in a complex domain
be a family of meromorphic functions in a complex domain  . Let
. Let  ,
,  such that
such that  . Let
. Let  ,
,  ,
,  ,
,  be positive integers such that
be positive integers such that  ,
,  ,
,  , and put
, and put

If there exists a positive constant  such that
such that  for all
for all  whenever
whenever  , then
, then  is a normal family.
is a normal family.
Theorem E.
Let  be a family of meromorphic functions in a complex domain
be a family of meromorphic functions in a complex domain  . Let
. Let  ,
,  such that
such that  . Let
. Let  ,
,  ,
,  ,
,  be nonnegative integers such that
be nonnegative integers such that  , and put
, and put

If there exists a positive constant  such that
such that  for all
for all  whenever
whenever  , then
, then  is a normal family.
is a normal family.
Very recently, Xu and Cao [10] further extended Theorems D and E by replacing  with
with  ; they got
; they got
Theorem F.
Let  be a family of meromorphic functions in a complex domain
be a family of meromorphic functions in a complex domain  , all of whose zeros have multiplicity at least
, all of whose zeros have multiplicity at least  . Let
. Let  such that
such that  . Let
. Let  ,
,  ,
,  ,
,  be nonnegative integers such that
be nonnegative integers such that  ,
,  ,
,  , (if
, (if  ,
,  ), and put
), and put

If there exists a positive constant  such that
such that  for all
for all  whenever
whenever  , then
, then  is a normal family.
is a normal family.
Theorem G.
Let  be a family of meromorphic functions in a complex domain
be a family of meromorphic functions in a complex domain  , all of whose zeros have multiplicity at least
, all of whose zeros have multiplicity at least  . Let
. Let  such that
such that  . Let
. Let  ,
,  ,
,  ,
,  be positive integers such that
be positive integers such that  , and put
, and put

If there exists a positive constant  such that
such that  for all
for all  whenever
whenever  , then
, then  is a normal family.
is a normal family.
To prove Theorems D–G, the authors used a key lemma (Lemma 2.4 in this paper) besides Zalcman-Pang's Lemma. It's natural to ask whether such normality criteria of Lahiri's type still hold for the general differential monomial  . We study this problem and obtain the following theorem
. We study this problem and obtain the following theorem
Theorem 1.1.
Let  be a family of meromorphic functions in a complex domain
be a family of meromorphic functions in a complex domain  , for every
, for every  , all zeros of
, all zeros of  have multiplicity at least
have multiplicity at least  . Let
. Let  ,
,  such that
such that  , let
, let  ,
,  ,
,  ,
,  ,
, 
 be nonnegative integers such that
be nonnegative integers such that

Put

If there exists a positive constant  such that
such that  for all
for all  whenever
whenever  , then
, then  is a normal family.
is a normal family.
Theorem 1.2.
Let  be a family of meromorphic functions in a complex domain
be a family of meromorphic functions in a complex domain  , for every
, for every  , all zeros of
, all zeros of  have multiplicity at least
have multiplicity at least  . Let
. Let  ,
,  such that
such that  , let
, let  ,
,  ,
,  ,
,  ,
,  be nonnegative integers such that
be nonnegative integers such that  , (
, ( when
when  or
or  ),
),  for all positive integers
for all positive integers  and
and  ,
,  . Put
. Put

If there exists a positive constant  such that
such that  for all
for all  whenever
whenever  , then
, then  is a normal family.
is a normal family.
As an application of Theorem 1.1, we obtain the following theorem.
Theorem 1.3.
Let  be a family of holomorphic functions in a domain
be a family of holomorphic functions in a domain  , for every
, for every  , all zeros of
, all zeros of  have multiplicity at least
have multiplicity at least  . Let
. Let  be two finite values and
be two finite values and  be nonnegative integers with
be nonnegative integers with  ,
,  ,
,  . For every
. For every  , all zeros of
, all zeros of  have multiplicity at least
have multiplicity at least  , if
, if  , then
, then  is normal in
is normal in  .
.
Example 1.4.
Let  and
and  . If
. If  , let
, let  . For each function
. For each function  ,
,  and
and  share 0 in
share 0 in  . However, it can be easily verified that
. However, it can be easily verified that  is not normal in
is not normal in  . Example 1.4 shows that the condition
. Example 1.4 shows that the condition  in Theorem 1.3 is sharp.
in Theorem 1.3 is sharp.
Example 1.5.
Let  and
and  . If
. If  , let
, let  , where
, where  is the root of
is the root of  . For each function
. For each function  ,
,  ,
,  in
in  . However, it can be easily verified that
. However, it can be easily verified that  is not normal in
is not normal in  . Example 1.5 shows that the multiplicity restriction on zeros of
. Example 1.5 shows that the multiplicity restriction on zeros of  in Theorem 1.3 is sharp (at least for
in Theorem 1.3 is sharp (at least for  ).
).
2. Preliminary Lemmas
Lemma 2.1 (see [11]).
Let  be a family of meromorphic functions on the unit disc
be a family of meromorphic functions on the unit disc  , all of whose zeros have the multiplicity at least
, all of whose zeros have the multiplicity at least  , then if
, then if  is not normal, there exist, for each
is not normal, there exist, for each 
(a)a number  ,
,  ,
,
(b)points  ,
,  ,
,
(c)functions  , and
, and
(d)positive numbers 
such that  locally uniformly with respect to the spherical metric, where
locally uniformly with respect to the spherical metric, where  is a nonconstant meromorphic function on
is a nonconstant meromorphic function on  , all of whose zeros have multiplicity at least
, all of whose zeros have multiplicity at least  , such that
, such that  . Here, as usual,
. Here, as usual,  is the spherical derivative.
is the spherical derivative.
Lemma 2.2 (see [1, page 158]).
Let  be a family of meromorphic functions in a domain
be a family of meromorphic functions in a domain  . Then
. Then  is normal in
is normal in  if and only if the spherical derivatives of functions
if and only if the spherical derivatives of functions  are uniformly bounded on each compact subset of
are uniformly bounded on each compact subset of  .
.
Lemma 2.3 (see [12]).
Let  be an entire function and
be an entire function and  a positive integer. If
a positive integer. If  for all
for all  , then
, then  has the order at most one.
has the order at most one.
Lemma 2.4 (see [13]).
Take nonnegative integers  with
with  ,
,  and define
and define  . Let
. Let  be a transcendental meromorphic function with the deficiency
be a transcendental meromorphic function with the deficiency  . Then for any nonzero value
. Then for any nonzero value  , the function
, the function  has infinitely many zeros. Moreover, if
has infinitely many zeros. Moreover, if  , the deficient condition can be omitted.
, the deficient condition can be omitted.
The following two lemmas can be seen as supplements of Lemma 2.4.
Lemma 2.5.
Take nonnegative integers  with
with  ,
,  and define
and define  . Let
. Let  be a transcendental meromorphic function whose zeros have multiplicity at least
be a transcendental meromorphic function whose zeros have multiplicity at least  . Then for any nonzero value
. Then for any nonzero value  , the function
, the function  has infinitely many zeros, provided that
has infinitely many zeros, provided that  and
and  when
when  . Specially, if
. Specially, if  is transcendental entire, the function
is transcendental entire, the function  has infinitely many zeros.
has infinitely many zeros.
Proof.
If  , then
, then  , this case has been considered (see [5, 12–20]).
, this case has been considered (see [5, 12–20]).
If  and if
and if  , we immediately get the conclusion from Lemma 2.4. Next we consider the case
, we immediately get the conclusion from Lemma 2.4. Next we consider the case  .
.
Let  . Using the proof of Lemma 2.4 (see [13, page 161–163] ), we obtain
. Using the proof of Lemma 2.4 (see [13, page 161–163] ), we obtain

Suppose that  is a zero of
is a zero of  of multiplicity
of multiplicity  , then
, then  is a zero of
is a zero of  of multiplicity
of multiplicity  , and thus is a pole of
, and thus is a pole of  of multiplicity
of multiplicity  . Thereby, from (2.1) we get
. Thereby, from (2.1) we get

Note that  , we deduce from (2.2) that
, we deduce from (2.2) that

If  , then
, then  ; this case has been proved as mentioned above (see [13–16]).
; this case has been proved as mentioned above (see [13–16]).
If  , then we have
, then we have  ; the conclusion is evident.
; the conclusion is evident.
If  , note that
, note that  and we deduce that
and we deduce that  , thus the conclusion holds.
, thus the conclusion holds.
If  is a transcendental entire function, we only need to consider the case
is a transcendental entire function, we only need to consider the case  . Note that (see Hu et al. [21, page 67])
. Note that (see Hu et al. [21, page 67])

With similar discussion as above, we obtain

In view of  and
and  , we get
, we get  , thus we immediately obtain the conclusion. This completes the proof of Lemma 2.5.
, thus we immediately obtain the conclusion. This completes the proof of Lemma 2.5.
Lemma 2.6.
Take nonnegative integers  with
with  ,
, ,
, and define
and define  . Let
. Let  be a nonconstant rational function whose zeros have multiplicity at least
be a nonconstant rational function whose zeros have multiplicity at least  . Then for any nonzero value
. Then for any nonzero value  , the function
, the function  has at least one finite zero.
has at least one finite zero.
Proof.
Since the case  has been proved by Charak and Rieppo [9], we only need to consider
has been proved by Charak and Rieppo [9], we only need to consider  .
.
Suppose that  has no zero.
has no zero.
Case 1.
If  is a nonconstant polynomial, since the zeros of
is a nonconstant polynomial, since the zeros of  have multiplicity at least
have multiplicity at least  , we know that
, we know that  is also a nonconstant polynomial, so
is also a nonconstant polynomial, so  has at least one zero, which contradicts our assumption.
has at least one zero, which contradicts our assumption.
Case 2.
If  is a nonconstant rational function but not a polynomial. Set
is a nonconstant rational function but not a polynomial. Set

where  is a nonzero constant and
is a nonzero constant and  ,
,  .
.
Then by mathematical induction, we get

where  ,
,  are constants and
are constants and


It is easily obtained that

Combining (2.6) and (2.7) yields

where  with
with  .
.
Moreover,  is not a constant, or else, we get
is not a constant, or else, we get  is a constant for
is a constant for  . The leading coefficient of
. The leading coefficient of  is
is  .
.
If  is a constant, then we get
is a constant, then we get

If  is a constant, then we get
is a constant, then we get

which implies  , a contradiction with the assumption
, a contradiction with the assumption  .
.
Then from (2.11), we obtain

where  is a polynomial with
is a polynomial with  .
.
Since  , we obtain from (2.11) that
, we obtain from (2.11) that

where  is a nonzero constant. Then
is a nonzero constant. Then

where  is a polynomial with
is a polynomial with  .
.
From (2.14) and (2.16), we deduce that

in view of  , together with (2.8), we have
, together with (2.8), we have

namely

which is a contradiction since  .
.
Hence  has at least one finite zero.
has at least one finite zero.
This proves Lemma 2.6.
Remark 2.7.
Lemma 2.6 is a generalization of Lemma 2.2 in [10]. The proof of Lemma 2.6 is quite different from its proof. Actually, the proof of Lemma 2.2 in [10] is incorrect. The main problem appears at (2.2) in [10]. Since  has only zero with multiplicity at least
has only zero with multiplicity at least  , then each zero of
, then each zero of  is of multiplicity at least
is of multiplicity at least  , but this does not mean that each zero of
, but this does not mean that each zero of  is of multiplicity at least
is of multiplicity at least  because the zeros of
because the zeros of  may not be the zeros of
may not be the zeros of  , and thus their multiplicity may less than
, and thus their multiplicity may less than  . Therefore, the inequality of (2.2) in [10] is not valid, which implies that the proof of Lemma 2.2 in [10] is not correct.
. Therefore, the inequality of (2.2) in [10] is not valid, which implies that the proof of Lemma 2.2 in [10] is not correct.
Lemma 2.8.
Let  ,
,  such that
such that  . Let
. Let  ,
,  ,
, 
 ,
,  ,
, 
 be nonnegative integers such that
be nonnegative integers such that  , (
, ( when
when  or
or  ),
),  for all positive integers
for all positive integers  and
and  ,
,  . Let
. Let  be a meromorphic function in
be a meromorphic function in  ; all zeros of
; all zeros of  have multiplicity at least
have multiplicity at least  . Define
. Define

Then  has a finite zero.
has a finite zero.
Proof.
The algebraic complex equation

has always a nonzero solution, say  . By Lemmas 2.5 and 2.6, the differential monomial
. By Lemmas 2.5 and 2.6, the differential monomial  cannot avoid it and thus there exists
cannot avoid it and thus there exists  such that
such that  .
.
Under the assumptions, for all positive integers  ,
,  ,
,  ,
,  , we have
, we have

Thus

This proves Lemma 2.8.
Lemma 2.9 (see [2, page 51]).
If  is an entire function of order
is an entire function of order  , then
, then

where  denotes the central-index of
denotes the central-index of  .
.
Lemma 2.10 (see [22, page 187–199] or [2, page 51]).
If  is a transcendental entire function, let
is a transcendental entire function, let  and
and  be such that
be such that  and that
and that  holds. Then there exists a set
holds. Then there exists a set  of finite logarithmic measure, that is,
of finite logarithmic measure, that is,  such that
such that

holds for all  and all
and all  .
.
3. Proof of Theorem 1.1
Without loss of generality, we may assume  . Suppose that
. Suppose that  is not normal at
is not normal at  . By Lemma 2.1, for
. By Lemma 2.1, for  , there exist
, there exist  ,
,  such that
such that  ,
,  and
and  such that
such that  locally uniformly with respect to the spherical metric, where
locally uniformly with respect to the spherical metric, where  is a nonconstant meromorphic function on
is a nonconstant meromorphic function on  , all of whose zeros have multiplicity at least
, all of whose zeros have multiplicity at least  . For simplicity, we denote
. For simplicity, we denote  by
by  . By Lemmas 2.4 and 2.6, there exists
. By Lemmas 2.4 and 2.6, there exists  such that
such that

Obviously,  , so in some neighborhood of
, so in some neighborhood of  ,
,  converges uniformly to
converges uniformly to  . We have
. We have

Let  , and under the assumption
, and under the assumption  , we obtain
, we obtain

is the uniform limit of

in some neighborhood of  .
.
By (3.1) and Hurwitz's theorem, there exists a sequence  such that for all large values of
such that for all large values of  and
and  ,
,

Hence for all large values of  ,
,  , it follows from the condition that
, it follows from the condition that

Since  is not a pole of
is not a pole of  , there exists a positive number
, there exists a positive number  such that in some neighborhood of
such that in some neighborhood of  we get
we get  .
.
Since  converges uniformly to
converges uniformly to  in some neighborhood of
in some neighborhood of  , we get for all large values of
, we get for all large values of  and for all
and for all  in that neighborhood of
in that neighborhood of 

By (3.7), we get

which is a contradiction since  as
as  .
.
This completes the proof of Theorem 1.1.
4. Proof of Theorem 1.2
Without loss of generality, we may assume  . Suppose that
. Suppose that  is not normal in
is not normal in  . By Lemma 2.1, for
. By Lemma 2.1, for  , there exist
, there exist  ,
,  ,
,  and
and  such that
such that  locally uniformly with respect to the spherical metric, where
locally uniformly with respect to the spherical metric, where  is a nonconstant meromorphic function on
is a nonconstant meromorphic function on  , all of whose zeros have multiplicity at least
, all of whose zeros have multiplicity at least  . By Lemma 2.8, we get
. By Lemma 2.8, we get

for some  .
.
We can arrive at a contradiction by using the same argument as in the latter part of proof of Theorem 1.1.
This completes the proof of Theorem 1.2.
5. Applications
Proof of Theorem 1.3.
We shall divide our argument into two cases.
Case 1 ( ).
).
Let  be a positive constant with
be a positive constant with  ; under the assumptions, we have
; under the assumptions, we have

and  for all
for all  whenever
whenever  ; by Lemmas 2.5 and 2.6, using the similar proof of Theorem 1.1, we obtain the conclusion.
; by Lemmas 2.5 and 2.6, using the similar proof of Theorem 1.1, we obtain the conclusion.
Case 2 ( ).
).
For  , if
, if  for
for  , since
, since  , we have
, we have  , which is a contradiction, hence
, which is a contradiction, hence  .
.
If  for
for  , since
, since  , we immediately get
, we immediately get  and hence
and hence  , which is still a contradiction, hence
, which is still a contradiction, hence  .
.
Suppose that  is not normal in
is not normal in  , by Lemma 2.1, there exist
, by Lemma 2.1, there exist  ,
,  ,
,  , and
, and  such that
such that  locally uniformly with respect to the spherical metric, where
locally uniformly with respect to the spherical metric, where  is a nonconstant entire function, all of whose zeros have multiplicity at least
is a nonconstant entire function, all of whose zeros have multiplicity at least  . By Hurwitz's theorem, we have
. By Hurwitz's theorem, we have
(i) or
or  , and
, and
(ii) or
or  .
.
Since  is not a constant, we have
is not a constant, we have  . By Lemma 2.3,
. By Lemma 2.3,  has the order at most 1, so
has the order at most 1, so  , where
, where  ,
,  are two constants. Thus
are two constants. Thus

If  , we immediately get a contradiction. Hence
, we immediately get a contradiction. Hence

but by Lemmas 2.5 and 2.6 we get a contradiction again.
This proves Theorem 5.1.
Further more, using Theorem 1.3, we obtain a uniqueness theorem related to R. Brück's Conjecture. Firstly, we recall this conjecture.
R. Brück's Conjecture
Let
 be a nonconstant entire function such that the hyper-order
be a nonconstant entire function such that the hyper-order
 is not a positive integer and
is not a positive integer and
 . If
. If
 and
and
 share a finite value
share a finite value
 CM, then
CM, then

where is a nonzero constant and the hyper-order
is a nonzero constant and the hyper-order is defined as follow:
is defined as follow:

Since then, many results related to this conjecture have been obtained. We refer the reader to Brück [23], Gundersen and Yang [24], Yang [25], Chen and Shon [26], Li and Gao [27], and Wang [28].
It's interesting to ask what happens if  is replaced by
is replaced by  in Brück's Conjecture. Recently, Yang and Zhang [29] considered this problem and got the following theorem.
in Brück's Conjecture. Recently, Yang and Zhang [29] considered this problem and got the following theorem.
Theorem H.
Let  be a nonconstant entire function.
be a nonconstant entire function.  be an integer, and let
be an integer, and let  . If
. If  and
and  share 1 CM, then
share 1 CM, then  , and
, and  assumes the form
assumes the form

where  is a nonzero constant.
is a nonzero constant.
Lü et al. [30] improves Theorem H and obtained the following theorem.
Theorem I.
Let  be a polynomial, and let
be a polynomial, and let  be an intege; let
be an intege; let  be a transcendental entire function, and let
be a transcendental entire function, and let  . If
. If  and
and  share
share  CM, then
CM, then

where  is a nonzero constant.
is a nonzero constant.
We obtain a more general result as follows.
Theorem 5.1.
Let  be nonnegative integers with
be nonnegative integers with  ,
,  ,
,  , and
, and  ,
,  be two finite nonzero values. Let
be two finite nonzero values. Let  be a nonconstant entire function whose zeros have multiplicity at least
be a nonconstant entire function whose zeros have multiplicity at least  . If
. If  , then
, then

where  is a nonzero constant. Specially, if
is a nonzero constant. Specially, if  , then
, then  , where
, where  is a nonzero constant,
is a nonzero constant,  is the root of
is the root of  .
.
Proof of Theorem 5.1.
First we assert that  . Let
. Let

Under the assumptions of Theorem 1.3, we get that  is a normal family of holomorphic functions in
is a normal family of holomorphic functions in  . By Lemma 2.2, there exists a constant
. By Lemma 2.2, there exists a constant  such that
such that

for all  . Hence by Lemma 2.3,
. Hence by Lemma 2.3,  has the order at most 1.
has the order at most 1.
Since  ,
,  must be a transcendental entire function and
must be a transcendental entire function and

From (5.11), we have  , hence
, hence  and
and  is a polynomial with
is a polynomial with  . Note that
. Note that  is transcendental, we have
is transcendental, we have  , as
, as  . Let
. Let  , where
, where  , we deduce
, we deduce

By Lemma 2.10, there exists a subset  of finite logarithmic measure, namely
of finite logarithmic measure, namely  such that for some point
such that for some point  satisfying
satisfying  and
and  , we obtain
, we obtain

as  .
.
Rewrite (5.11) as

it follows from (5.12)–(5.14) and Lemma 2.8 that

as  . Since
. Since  is a polynomial, from (5.15), we deduce that
is a polynomial, from (5.15), we deduce that  is a constant. Let
is a constant. Let  , then
, then  is a nonzero constant. Thus
is a nonzero constant. Thus

Specially, if  , suppose that
, suppose that  has a zero
has a zero  , by letting
, by letting  in (5.16), we get
in (5.16), we get  ; hence
; hence

Suppose that  is a zero of
is a zero of  with multiplicity
with multiplicity  , then
, then  is a zero of
is a zero of  with multiplicity
with multiplicity  , and a zero of
, and a zero of  with multiplicity
with multiplicity  , which is a contradiction. So
, which is a contradiction. So  has no zero, note that
has no zero, note that  is a transcendental entire function and
is a transcendental entire function and  , we have
, we have  , where
, where  and
and  are two finite nonzero values. In view of (5.16) and
are two finite nonzero values. In view of (5.16) and  , we deduce that
, we deduce that

hence  and
and  .
.  ,
,  is the root of
is the root of  .
.
This completes the proof of Theorem 5.1.
References
Hayman WK: Meromorphic Functions, Oxford Mathematical Monographs. Oxford University Press, London, UK; 1964:xiv+191.
Laine I: Nevanlinna Theory and Complex Differential Equations, de Gruyter Studies in Mathematics. Volume 15. Walter de Gruyter, Berlin, Germany; 1993:viii+341.
Yang C-C, Yi H-X: Uniqueness Theory of Meromorphic Functions, Mathematics and Its Applications. Volume 557. Kluwer Academic Publishers Group, Dordrecht, The Netherlands; 2003:viii+569.
Yang L: Value Distribution Theory. Springer, Berlin, Germany; 1993:xii+269.
Hayman WK: Picard values of meromorphic functions and their derivatives. Annals of Mathematics 1959, 70: 9–42. 10.2307/1969890
Pang XC: Bloch's principle and normal criterion. Science in China 1989,32(7):782–791.
Pang XC: On normal criterion of meromorphic functions. Science in China 1990,33(5):521–527.
Lahiri I: A simple normality criterion leading to a counterexample to the converse of the Bloch principle. New Zealand Journal of Mathematics 2005,34(1):61–65.
Charak KS, Rieppo J: Two normality criteria and the converse of the Bloch principle. Journal of Mathematical Analysis and Applications 2009,353(1):43–48. 10.1016/j.jmaa.2008.11.066
Xu J, Cao W: Some normality criteria of meromorphic functions. Journal of Inequalities and Applications 2010, 2010:-10.
Pang X, Zalcman L: Normal families and shared values. The Bulletin of the London Mathematical Society 2000,32(3):325–331. 10.1112/S002460939900644X
Clunie J, Hayman WK: The spherical derivative of integral and meromorphic functions. Commentarii Mathematici Helvetici 1966, 40: 117–148.
Yang CC, Hu PC: On the value distribution of
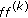 . Kodai Mathematical Journal 1996,19(2):157–167. 10.2996/kmj/1138043595
. Kodai Mathematical Journal 1996,19(2):157–167. 10.2996/kmj/1138043595Alotaibi A: On the zeros of
 for
for  . Computational Methods and Function Theory 2004,4(1):227–235.
. Computational Methods and Function Theory 2004,4(1):227–235.Bergweiler W, Eremenko A: On the singularities of the inverse to a meromorphic function of finite order. Revista Matemática Iberoamericana 1995,11(2):355–373.
Chen HH, Fang ML: The value distribution of
 . Science in China 1995,38(7):789–798.
. Science in China 1995,38(7):789–798.Hayman WK: Research Problems in Function Theory. The Athlone Press, London, UK; 1967:vii+56.
Mues E: Über ein problem von Hayman. Mathematische Zeitschrift 1979,164(3):239–259. 10.1007/BF01182271
Pang X, Zalcman L: On theorems of Hayman and Clunie. New Zealand Journal of Mathematics 1999,28(1):71–75.
Wang JP: A fundamental inequality of the theory of meromorphic functions and its applications. Acta Mathematica Sinica. Chinese Series 2006,49(2):443–450.
Hu P-C, Li P, Yang C-C: Unicity of Meromorphic Mappings, Advances in Complex Analysis and Its Applications. Volume 1. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2003:x+467.
Jank G, Volkmann L: Einführung in die Theorie der Ganzen und Meromorphen Funktionen mit Anwendungen auf Differentialgleichungen. Birkhäuser, Basel, Switzerland; 1985:256.
Brück R: On entire functions which share one value CM with their first derivative. Results in Mathematics 1996,30(1–2):21–24.
Gundersen GG, Yang L-Z: Entire functions that share one value with one or two of their derivatives. Journal of Mathematical Analysis and Applications 1998,223(1):88–95. 10.1006/jmaa.1998.5959
Yang L-Z: Solution of a differential equation and its applications. Kodai Mathematical Journal 1999,22(3):458–464. 10.2996/kmj/1138044097
Chen Z-X, Shon KH: On conjecture of R. Brück concerning the entire function sharing one value CM with its derivative. Taiwanese Journal of Mathematics 2004,8(2):235–244.
Li X-M, Gao C-C: Entire functions sharing one polynomial with their derivatives. Proceedings of the Indian Academy of Sciences 2008,118(1):13–26. 10.1007/s12044-008-0002-z
Wang J: Uniqueness of entire function sharing a small function with its derivative. Journal of Mathematical Analysis and Applications 2010,362(2):387–392. 10.1016/j.jmaa.2009.09.052
Yang L-Z, Zhang J-L: Non-existence of meromorphic solutions of a Fermat type functional equation. Aequationes Mathematicae 2008,76(1–2):140–150. 10.1007/s00010-007-2913-7
Lü F, Xu J, Chen A: Entire functions sharing polynomials with their first derivatives. Archiv der Mathematik 2009,92(6):593–601. 10.1007/s00013-009-3075-8
Acknowledgments
The authors thank the referees for reading the manuscript very carefully and making a number of valuable suggestions to improve the readability of the paper. The authors were supported by NSF of China (no. 10771121), NSF of Shandong Province (no. Z2008A01) and NSF of Guangdong Province (no. 9452902001003278).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhang, XB., Xu, JF. & Yi, HX. Normality Criteria of Lahiri's Type and Their Applications. J Inequal Appl 2011, 873184 (2011). https://doi.org/10.1155/2011/873184
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/873184
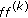 . Kodai Mathematical Journal 1996,19(2):157–167. 10.2996/kmj/1138043595
. Kodai Mathematical Journal 1996,19(2):157–167. 10.2996/kmj/1138043595 for
for  . Computational Methods and Function Theory 2004,4(1):227–235.
. Computational Methods and Function Theory 2004,4(1):227–235. . Science in China 1995,38(7):789–798.
. Science in China 1995,38(7):789–798.