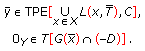- Research Article
- Open access
- Published:
Tightly Proper Efficiency in Vector Optimization with Nearly Cone-Subconvexlike Set-Valued Maps
Journal of Inequalities and Applications volume 2011, Article number: 839679 (2011)
Abstract
A scalarization theorem and two Lagrange multiplier theorems are established for tightly proper efficiency in vector optimization involving nearly cone-subconvexlike set-valued maps. A dual is proposed, and some duality results are obtained in terms of tightly properly efficient solutions. A new type of saddle point, which is called tightly proper saddle point of an appropriate set-valued Lagrange map, is introduced and is used to characterize tightly proper efficiency.
1. Introduction
One important problem in vector optimization is to find efficient points of a set. As observed by Kuhn, Tucker and later by Geoffrion, some efficient points exhibit certain abnormal properties. To eliminate such abnormal efficient points, there are many papers to introduce various concepts of proper efficiency; see [1–8]. Particularly, Zaffaroni [9] introduced the concept of tightly proper efficiency and used a special scalar function to characterize the tightly proper efficiency, and obtained some properties of tightly proper efficiency. Zheng [10] extended the concept of superefficiency from normed spaces to locally convex topological vector spaces. Guerraggio et al. [11] and Liu and Song [12] made a survey on a number of definitions of proper efficiency and discussed the relationships among these efficiencies, respectively.
Recently, several authors have turned their interests to vector optimization of set-valued maps, for instance, see [13–18]. Gong [19] discussed set-valued constrained vector optimization problems under the constraint ordering cone with empty interior. Sach [20] discussed the efficiency, weak efficiency and Benson proper efficiency in vector optimization problem involving ic-cone-convexlike set-valued maps. Li [21] extended the concept of Benson proper efficiency to set-valued maps and presented two scalarization theorems and Lagrange mulitplier theorems for set-valued vector optimization problem under cone-subconvexlikeness. Mehra [22], Xia and Qiu [23] discussed the superefficiency in vector optimization problem involving nearly cone-convexlike set-valued maps, nearly cone-subconvexlike set-valued maps, respectively. For other results for proper efficiencies in optimization problems with generalized convexity and generalized constraints, we refer to [24–26] and the references therein.
In this paper, inspired by [10, 21–23], we extend the concept of tight properness from normed linear spaces to locally convex topological vector spaces, and study tightly proper efficiency for vector optimization problem involving nearly cone-subconvexlike set-valued maps and with nonempty interior of constraint cone in the framework of locally convex topological vector spaces.
The paper is organized as follows. Some concepts about tightly proper efficiency, superefficiency and strict efficiency are introduced and a lemma is given in Section 2. In Section 3, the relationships among the concepts of tightly proper efficiency, strict efficiency and superefficiency in local convex topological vector spaces are clarified. In Section 4, the concept of tightly proper efficiency for set-valued vector optimization problem is introduced and a scalarization theorem for tightly proper efficiency in vector optimization problems involving nearly cone-subconvexlike set-valued maps is obtained. In Section 5, we establish two Lagrange multiplier theorems which show that tightly properly efficient solution of the constrained vector optimization problem is equivalent to tightly properly efficient solution of an appropriate unconstrained vector optimization problem. In Section 6, some results on tightly proper duality are given. Finally, a new concept of tightly proper saddle point for set-valued Lagrangian map is introduced and is then utilized to characterize tightly proper efficiency in Section 7. Section 8 contains some remarks and conclusions.
2. Preliminaries
Throughout this paper, let  be a linear space,
be a linear space,  and
and  be two real locally convex topological spaces (in brief, LCTS), with topological dual spaces
be two real locally convex topological spaces (in brief, LCTS), with topological dual spaces  and
and  , respectively. For a set
, respectively. For a set  ,
,  ,
,  ,
,  , and
, and  denote the closure, the interior, the boundary, and the complement of
denote the closure, the interior, the boundary, and the complement of  , respectively. Moreover, by
, respectively. Moreover, by  we denote the closed unit ball of
we denote the closed unit ball of  . A set
. A set  is said to be a cone if
is said to be a cone if  for any
for any  and
and  . A cone
. A cone  is said to be convex if
is said to be convex if  , and it is said to be pointed if
, and it is said to be pointed if  . The generated cone of
. The generated cone of  is defined by
is defined by

The dual cone of  is defined as
is defined as

and the quasi-interior of  is the set
is the set

Recall that a base of a cone  is a convex subset of
is a convex subset of  such that
such that

Of course,  is pointed whenever
is pointed whenever  has a base. Furthermore, if
has a base. Furthermore, if  is a nonempty closed convex pointed cone in
is a nonempty closed convex pointed cone in  , then
, then  if and only if
if and only if  has a base.
has a base.
Also, in this paper, we assume that, unless indicated otherwise,  and
and  are pointed closed convex cones with
are pointed closed convex cones with  and
and  , respectively.
, respectively.
Definition 2.1 (see [27]).
Let  be a base of
be a base of  . Define
. Define

Cheng and Fu in [27] discussed the propositions of  , and the following remark also gives some propositions of
, and the following remark also gives some propositions of  .
.
Remark 2.2 (see [27]).
-
(i)
Let
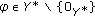 . Then
. Then 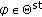 if and only if there exists a neighborhood
if and only if there exists a neighborhood  of
of 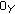 such that
such that 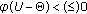 .
. -
(ii)
If
 is a bounded base of
is a bounded base of 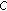 , then
, then  .
.
Definition 2.3.
A point  is said to be efficient with respect to
is said to be efficient with respect to  (denoted
(denoted  ) if
) if

Remark 2.4 (see [28]).
If  is a closed convex pointed cone and
is a closed convex pointed cone and  , then
, then  .
.
In [10], Zheng generalized two kinds of proper efficiency, namely, Henig proper efficiency and superefficiency, from normed linear spaces to LCTS. And Fu [8] generalized a kind of proper efficiency, namely strict efficiency, from normed linear spaces to LCTS. Let  be an ordering cone with a base
be an ordering cone with a base  . Then
. Then  , by the Hahn Banach separation theorem, there are a
, by the Hahn Banach separation theorem, there are a  and an
and an  such that
such that

Let  . Then
. Then  is a neighborhood of
is a neighborhood of  and
and

It is clear that, for each convex neighborhood  of
of  with
with  ,
,  is convex and
is convex and  . Obviously,
. Obviously,  is convex pointed cone, indeed,
is convex pointed cone, indeed,  is also a base of
is also a base of  .
.
Definition 2.5 (see [8]).
Suppose that  is a subset of
is a subset of  and
and  denotes the family of all bases of
denotes the family of all bases of  .
.  is said to be a strictly efficient point with respect to
is said to be a strictly efficient point with respect to  , written as
, written as  , if there is a convex neighborhood
, if there is a convex neighborhood  of
of  such that
such that

 is said to be a strictly efficient point with respect to
is said to be a strictly efficient point with respect to  , written as,
, written as,  if
if

Remark 2.6.
Since  is open in
is open in  , thus
, thus  is equivalent to
is equivalent to  .
.
Definition 2.7.
The point  is called tightly properly efficient with respect to
is called tightly properly efficient with respect to  (denoted
(denoted  ) if there exists a convex cone
) if there exists a convex cone  with
with  satisfying
satisfying  and there exists a neighborhood
and there exists a neighborhood  of
of  such that
such that

 is said to be a tightly properly efficient point with respect to
is said to be a tightly properly efficient point with respect to  , written as,
, written as,  if
if

Now, we give the following example to illustrate Definition 2.7.
Example 2.8.
Let  ,
,  . Given
. Given  (see Figure 1). Thus, it follows from the direct computation and Definition 2.7 that
(see Figure 1). Thus, it follows from the direct computation and Definition 2.7 that

Remark 2.9.
By Definitions 2.7 and 2.3, it is easy to verify that

but, in general, the converse is not valid. The following example illustrates this case.
Example 2.10.
 ,
,  , and
, and  . Then, by Definitions 2.3 and 2.7, we get
. Then, by Definitions 2.3 and 2.7, we get

thus,  .
.
Definition 2.11 (see [10]).
 is called a superefficient point of a subset
is called a superefficient point of a subset  of
of  with respect to ordering cone
with respect to ordering cone  , written as
, written as  , if, for each neighborhood
, if, for each neighborhood  of
of  , there is neighborhood
, there is neighborhood  of
of  such that
such that

Definition 2.12 (see [29, 30]).
A set-valued map  is said to be nearly
is said to be nearly  -subconvexlike on
-subconvexlike on  if
if  is convex.
is convex.
Given the two set-valued maps  ,
,  , let
, let

The product  is called nearly
is called nearly  -subconvexlike on
-subconvexlike on  if
if  is nearly
is nearly  -subconvexlike on
-subconvexlike on  . Let
. Let  be the space of continuous linear operators from
be the space of continuous linear operators from  to
to  , and let
, and let

Denote by  the set-valued map from
the set-valued map from  to
to  defined by
defined by

If  ,
,  , we also define
, we also define  and
and  by
by

respectively.
Lemma 2.13 (see [23]).
If  is nearly
is nearly  -subconvexlike on
-subconvexlike on  , then:
, then:
(i)for each  ,
,  is nearly
is nearly  -subconvexlike on
-subconvexlike on  ;
;
(ii)for each  ,
,  is nearly
is nearly  -subconvexlike on
-subconvexlike on  .
.
3. Tightly Proper Efficiency, Strict Efficiency, and Superefficiency
In [11, 12], the authors introduced many concepts of proper efficiency (tightly proper efficiency except) for normed spaces and for topological vector spaces, respectively. Furthermore, they discussed the relationships between superefficiency and other proper efficiencies. If we can get the relationship between tightly proper efficiency and superefficiency, then we can get the relationships between tightly proper efficiency and other proper efficiencies. So, in this section, the aim is to get the equivalent relationships between tightly proper efficiency and superefficiency under suitable assumption by virtue of strict efficiency.
Lemma 3.1.
If  has a bounded base
has a bounded base  , then
, then

Proof.
From the definition of  and
and  , we only need prove that
, we only need prove that  for any
for any  . Indeed, for each
. Indeed, for each  , by the separation theorem, there exists
, by the separation theorem, there exists  such that
such that

Hence,  . Since
. Since  is bounded, there exists
is bounded, there exists  such that
such that

It is clear that  and
and  . If there exists
. If there exists  such that
such that  , then for any convex cone
, then for any convex cone  with
with  satisfying
satisfying  and for any neighborhood
and for any neighborhood  of
of  such that
such that

It implies that there exists  such that
such that

Then there is  and
and  such that
such that  , since
, since  , then there exists
, then there exists  and
and  such that
such that  . By (3.2) and (3.3), we see that
. By (3.2) and (3.3), we see that  . Therefore,
. Therefore,  and
and  , it is a contradiction. Therefore,
, it is a contradiction. Therefore,  for each
for each  .
.
Proposition 3.2.
If  has a bounded base
has a bounded base  , then
, then

Proof.
By Definition 2.11, for any  , there exists a convex neighborhood
, there exists a convex neighborhood  of
of  with
with  such that
such that

It is easy to verify that

Now, let  and by Lemma 3.1, we have
and by Lemma 3.1, we have

which implies that  .
.
Proposition 3.3.
Let  . Then
. Then

Proof.
For each  , there exists a convex cone
, there exists a convex cone  with
with  satisfying
satisfying

and there exists a neighborhood  of
of  such that
such that

Since expression (3.11) can be equivalently expressed as

 , and by (3.12), we have
, and by (3.12), we have

Since  is open in
is open in  , we get
, we get

It implies that  . Therefore this proof is completed.
. Therefore this proof is completed.
Remark 3.4.
If  does not have a bounded base, then the converse of Proposition 3.3 may not hold. The following example illustrates this case.
does not have a bounded base, then the converse of Proposition 3.3 may not hold. The following example illustrates this case.
Example 3.5.
Let  ,
,  (see Figure 2) and
(see Figure 2) and  .
.
Then, let  , we have
, we have  . It follows from the definitions of
. It follows from the definitions of  and
and  that
that

respectively. Thus, the converse of Proposition 3.3 is not valid.
Proposition 3.6 (see [8]).
If  has a bounded base
has a bounded base  , then
, then

From Propositions 3.2, 3.3, and 3.6, we can get immediately the following corollary.
Corollary 3.7.
If  has a bounded base
has a bounded base  , then
, then

Example 3.8.
Let  ,
,  be given in Example 3.5 and
be given in Example 3.5 and  . Then
. Then

Lemma 3.9 (see [23]).
Let  be a closed convex pointed cone with a bounded base
be a closed convex pointed cone with a bounded base  and
and  . Then,
. Then,  .
.
From Corollary 3.7 and Lemma 3.9, we can get the following proposition.
Proposition 3.10.
If  has a bounded base
has a bounded base  and
and  is a nonempty subset of
is a nonempty subset of  , then
, then  .
.
4. Tightly Proper Efficiency and Scalarization
Let  be a closed convex pointed cone. We consider the following vector optimization problem with set-valued maps
be a closed convex pointed cone. We consider the following vector optimization problem with set-valued maps

where  ,
,  are set-valued maps with nonempty values. Let
are set-valued maps with nonempty values. Let  be the set of all feasible solutions of (VP).
be the set of all feasible solutions of (VP).
Definition 4.1.
 is said to be a tightly properly efficient solution of (VP), if there exists
is said to be a tightly properly efficient solution of (VP), if there exists  such that
such that  .
.
We call  is a tightly properly efficient minimizer of (VP). The set of all tightly properly efficient solutions of (VP) is denoted by TPE(VP).
is a tightly properly efficient minimizer of (VP). The set of all tightly properly efficient solutions of (VP) is denoted by TPE(VP).
In association with the vector optimization problem (VP) of set-valued maps, we consider the following scalar optimization problem with set-valued map  :
:

where  . The set of all optimal solutions of ( ) is denoted by
. The set of all optimal solutions of ( ) is denoted by  , that is,
, that is,

The fundamental results characterize tightly properly efficient solution of (VP) in terms of the solutions of ( ) are given below.
Theorem 4.2.
Let the cone  have a bounded base
have a bounded base  . Let
. Let  ,
,  , and
, and  be nearly
be nearly  -subconvexlike on
-subconvexlike on  . Then
. Then  if and only if there exists
if and only if there exists  such that
such that  .
.
Proof.
Necessity. Let  . Then, by Lemma 3.1 and Proposition 3.10, we have
. Then, by Lemma 3.1 and Proposition 3.10, we have  . Hence, there exists a convex cone
. Hence, there exists a convex cone  with
with  satisfying
satisfying  and there exists a convex neighborhood
and there exists a convex neighborhood  of
of  such that
such that

From the above expression and  , we have
, we have

Since  is open in
is open in  , we have
, we have

By the assumption that  is nearly
is nearly  -subconvexlike on
-subconvexlike on  , thus
, thus  is convex set. By the Hahn-Banach separation theorem, there exists
is convex set. By the Hahn-Banach separation theorem, there exists  such that
such that

It is easy to see that

Hence, we obtain

Furthermore, according to Remark 2.2, we have  .
.
Sufficiency. Suppose that there exists  such that
such that  . Since
. Since  has a bounded base
has a bounded base  , thus by Remark 2.2(ii), we know that
, thus by Remark 2.2(ii), we know that  . And by Remark 2.2(i), we can take a convex neighborhood
. And by Remark 2.2(i), we can take a convex neighborhood  of
of  such that
such that

By  , we have
, we have

From the above expression and (4.8), we get

Therefore,  . Noting that
. Noting that  has a bounded base
has a bounded base  and by Lemma 3.1, we have
and by Lemma 3.1, we have  .
.
Now, we give the following example to illustrate Theorem 4.2.
Example 4.3.
Let  ,
,  and
and  . Given
. Given  ,
,  . Let
. Let

Thus, feasible set of (VP)

By Definition 4.1, we get

For any point  , there exists
, there exists  such that
such that

Indeed, for any  , we consider the following three cases.
, we consider the following three cases.
Case 1.
If  is in the first quadrant, then for any
is in the first quadrant, then for any  such that
such that  .
.
Case 2.
If  is in the second quadrant, then there exists
is in the second quadrant, then there exists  such that
such that  . Let
. Let  such that
such that

Then, we have

Case 3.
If  in the fourth quadrant, then there exists
in the fourth quadrant, then there exists  such that
such that  . Let
. Let  such that
such that

Then, we have

Therefore, if follows from Cases 1, 2, and 3 that there exists  such that
such that  .
.
From Theorem 4.2, we can get immediately the following corollary.
Corollary 4.4.
Let the cone  have a bounded base
have a bounded base  . For any
. For any  if
if  is nearly
is nearly  -subconvexlike on
-subconvexlike on  . Then
. Then

5. Tightly Proper Efficiency and the Lagrange Multipliers
In this section, we establish two Lagrange multiplier theorems which show that tightly properly efficient solution of the constrained vector optimization problem (VP), is equivalent to tightly properly efficient solution of an appropriate unconstrained vector optimization problem.
Definition 5.1 (see [17]).
Let  be a closed convex pointed cone with
be a closed convex pointed cone with  . We say that (VP) satisfies the generalized Slater constraint qualification, if there exists
. We say that (VP) satisfies the generalized Slater constraint qualification, if there exists  such that
such that

Theorem 5.2.
Let  have a bounded base
have a bounded base  and
and  . Let
. Let  ,
,  and
and  is nearly
is nearly  -subconvexlike on
-subconvexlike on  . Furthermore, let (VP) satisfies the generalized Slater constraint qualification. If
. Furthermore, let (VP) satisfies the generalized Slater constraint qualification. If  and
and  , then there exists
, then there exists  such that
such that

Proof.
Since  has bounded base
has bounded base  , by Lemma 2.13, we have
, by Lemma 2.13, we have  . Thus, there is a convex cone
. Thus, there is a convex cone  with
with  satisfying
satisfying

and there exists an absolutely convex open neighborhood  of
of  such that
such that

Since (5.3) is equivalent to  , and from (5.4) we see that
, and from (5.4) we see that

Moreover, for any  , we have
, we have  . Therefore,
. Therefore,

Since  is open in
is open in  , thus, we get
, thus, we get

By the assumption that  is nearly
is nearly  -subconvexlike on
-subconvexlike on  , we have
, we have

is convex. Hence, it follows from the Hahn-Banach separation theorem that there exists  such that
such that

Thus, we obtain


Since  is a cone, we get
is a cone, we get


Since  ,
,  . Choose
. Choose  . By (5.13), we know that
. By (5.13), we know that  , thus
, thus

Letting  and noting that
and noting that  ,
,  in (5.10), we get
in (5.10), we get

Thus,  , which implies
, which implies

Now, we claim that  . If this is not the case, then
. If this is not the case, then

By the generalized Slater constraint qualification, then there exists  such that
such that

and so there exists  such that
such that  . Hence,
. Hence,  . But substituting
. But substituting  into (5.10), and by taking
into (5.10), and by taking  , and
, and  in (5.10), we have
in (5.10), we have

This contradiction shows that  . Therefore
. Therefore  . From (5.12) and Remark 2.2, we have
. From (5.12) and Remark 2.2, we have  . And since
. And since  is a bounded base of
is a bounded base of  , so
, so  . Hence, we can choose
. Hence, we can choose  such that
such that  and define the operator
and define the operator  by
by

Clearly,  and by (5.16), we see that
and by (5.16), we see that

Therefore,

From (5.10) and (5.20), we obtain

Since  is nearly
is nearly  -subconvexlike on
-subconvexlike on  , by Lemma 2.13, we have
, by Lemma 2.13, we have  is nearly
is nearly  -subconvexlike on
-subconvexlike on  . From (5.22), Theorem 4.2 and the above expression, we have
. From (5.22), Theorem 4.2 and the above expression, we have

Therefore, the proof is completed.
Theorem 5.3.
Let  be a closed convex pointed cone with a bounded base
be a closed convex pointed cone with a bounded base  ,
,  and
and  . If there exists
. If there exists  such that
such that  and
and  , then
, then  and
and  .
.
Proof.
Since  has a bounded base, and
has a bounded base, and  , we have
, we have  . Thus, there exists a convex cone
. Thus, there exists a convex cone  with
with  satisfying
satisfying

and there exits a convex neighborhood  of
of  such that
such that

By  , we have
, we have

Thus,

Therefore, by the definition of  and
and  , we get
, we get  and
and  , respectively.
, respectively.
6. Tightly Proper Efficiency and Duality
Definition 6.1.
The set-valued Lagrangian map  for problem (VP) is defined by
for problem (VP) is defined by

Definition 6.2.
The set-valued map  , defined by
, defined by

is called a tightly properly dual map for (VP). We now associate the following Lagrange dual problem with (VP):

Definition 6.3.
A point  is said to be an efficient point of (VD) if
is said to be an efficient point of (VD) if

We now can establish the following dual theorems.
Theorem 6.4 (weak duality).
If  and
and  . Then
. Then

Proof.
One has

Then, there exists  such that
such that

Hence,

Particularly,

Noting that

and taking  in (6.8), we have
in (6.8), we have

Hence, from  and
and  , we get
, we get

This completes the proof.
Theorem 6.5 (strong duality).
Let  be a closed convex pointed cone with a bounded base
be a closed convex pointed cone with a bounded base  in
in  and
and  be a closed convex pointed cone with
be a closed convex pointed cone with  in
in  . Let
. Let  ,
,  ,
,  be nearly
be nearly  -subconvexlike on
-subconvexlike on  . Furthermore, let (VP) satisfy the generalized Slater constraint qualification. Then,
. Furthermore, let (VP) satisfy the generalized Slater constraint qualification. Then,  and
and  if and only if
if and only if  is an efficient point of (VD).
is an efficient point of (VD).
Proof.
Let  and
and  , then according to Theorem 5.2, there exists
, then according to Theorem 5.2, there exists  such that
such that  and
and  . Hence
. Hence

By Theorem 6.4, we know that  is an efficient point of (VD).
is an efficient point of (VD).
Conversely, Since  is an efficient point of (VD), then
is an efficient point of (VD), then  . Hence, there exists
. Hence, there exists  such that
such that

Since  has a bounded base
has a bounded base  , by Lemma 3.1 and Proposition 3.10, we have
, by Lemma 3.1 and Proposition 3.10, we have

Hence, there exists a convex cone  with
with  satisfying
satisfying  and there exists an absolutely open convex neighborhood
and there exists an absolutely open convex neighborhood  of
of  such that
such that

Hence, we have

Since,  is open subset of
is open subset of  , we have
, we have

Since  is nearly
is nearly  -subconvexlike on
-subconvexlike on  , by Lemma 2.13, we have
, by Lemma 2.13, we have  is nearly
is nearly  -subconvexlike on
-subconvexlike on  , which implies that
, which implies that

is convex. From (6.17) and by the Hahn-Banach separation theorem, there exists  such that
such that

From this, we have


From (6.21), we know that  . And by
. And by  is bounded base of
is bounded base of  , it implies that
, it implies that  . For any
. For any  , there exists
, there exists  . Since
. Since  , we have
, we have  and hence
and hence  . From this and (6.20), we have
. From this and (6.20), we have

that is  . By Theorem 4.2, we have
. By Theorem 4.2, we have  and
and  .
.
7. Tightly Proper Efficiency and Tightly Proper Saddle Point
We now introduce a new concept of tightly proper saddle point for a set-valued Lagrange map  and use it to characterize tightly proper efficiency.
and use it to characterize tightly proper efficiency.
Definition 7.1.
Let  ,
,  is a closed convex pointed cone of
is a closed convex pointed cone of  and
and  .
.  if there exists a convex cone
if there exists a convex cone  with
with  satisfying
satisfying  and there is a convex neighborhood
and there is a convex neighborhood  of
of  such that
such that

 is said to be a tightly properly efficient point with respect to
is said to be a tightly properly efficient point with respect to  , written as,
, written as,  if
if

It is easy to find that  if and only if
if and only if  , and if
, and if  is bounded, then we also have
is bounded, then we also have  .
.
Definition 7.2.
A pair  is said to be a tightly proper saddle point of Lagrangian map
is said to be a tightly proper saddle point of Lagrangian map  if
if

We first present an important equivalent characterization for a tightly proper saddle point of the Lagrange map  .
.
Lemma 7.3.
 is said to be a tight proper saddle point of Lagrange map
is said to be a tight proper saddle point of Lagrange map  if only if there exist
if only if there exist  and
and  such that
such that
(i) ,
,
(ii) .
.
Proof.
Necessity. Since  is a tightly proper saddle point of
is a tightly proper saddle point of  , by Definition 7.2 there exist
, by Definition 7.2 there exist  and
and  such that
such that


From (7.5) and the definition of  , then there exists a convex cone
, then there exists a convex cone  with
with  satisfying
satisfying

and there is a convex neighborhood  of
of  such that
such that

Since, for every  ,
,

We have

Thus, from (7.6), we have

Let  be defined by
be defined by

Then, (7.10) can be written as

By (7.7) and the above expression show that  is a tightly properly efficient point of the vector optimization problem
is a tightly properly efficient point of the vector optimization problem

Since  is a linear map, of course,
is a linear map, of course,  is nearly
is nearly  -subconvexlike on
-subconvexlike on  . Hence, by Theorem 4.2, there exists
. Hence, by Theorem 4.2, there exists  such that
such that

Now, we claim that

If this is not true, then since  is a closed convex cone set, by the strong separation theorem in topological vector space, there exists
is a closed convex cone set, by the strong separation theorem in topological vector space, there exists  such that
such that

In the above expression, taking  gets
gets

while letting  leads to
leads to

Hence,

Let  be fixed, and define
be fixed, and define  as
as

It is evident that  and that
and that

Hence,  . And taking
. And taking  in (7.20), we obtain
in (7.20), we obtain

Hence,

which contradicts (7.14). Therefore,

Thus,  , and since
, and since  . If
. If  , then
, then

hence  , by
, by  . But, taking
. But, taking  in (7.14) leads to
in (7.14) leads to

This contradiction shows that  , that is, condition (ii) holds.
, that is, condition (ii) holds.
Therefore, by (7.4) and (7.5), we know

that is condition (i) holds.
Sufficiency. From  ,
,  , and condition (ii), we get
, and condition (ii), we get

And by condition (i), we obtain

Therefore,  is a tightly proper saddle point of
is a tightly proper saddle point of  , and the proof is completed.
, and the proof is completed.
The following saddle-point theorem allows us to express a tightly properly efficient solution of (VP) as a tightly proper saddle of the set-valued Lagrange map  .
.
Theorem 7.4.
Let  be nearly
be nearly  -convexlike on
-convexlike on  . If for any point
. If for any point  such that
such that  is nearly
is nearly  -convexlike on
-convexlike on  , and (VP) satisfy generalized Slater constraint qualification.
, and (VP) satisfy generalized Slater constraint qualification.
(i)If  is a tightly proper saddle point of
is a tightly proper saddle point of  , then
, then  is a tightly properly efficient solution of (VP).
is a tightly properly efficient solution of (VP).
(ii)If  be a tightly properly efficient minimizer of (VP),
be a tightly properly efficient minimizer of (VP),  . Then there exists
. Then there exists  such that
such that  is a tightly proper saddle point of Lagrange map
is a tightly proper saddle point of Lagrange map  .
.
Proof.
-
(i)
By the necessity of Lemma 7.3, we have
 (7.30)
(7.30)
and there exists  such that
such that  is a tightly properly efficient minimizer of the problem
is a tightly properly efficient minimizer of the problem

According to Theorem 5.3,  is a tightly properly efficient minimizer of (VP). Therefore,
is a tightly properly efficient minimizer of (VP). Therefore,  is a tightly properly efficient solution of (VP).
is a tightly properly efficient solution of (VP).
-
(ii)
From the assumption, and by Theorem 5.2, there exists
 such that
such that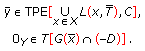 (7.31)
(7.31)
Therefore there exists  such that
such that  . Hence, from Lemma 7.3, it follows that
. Hence, from Lemma 7.3, it follows that  is a tightly proper saddle point of Lagrange map
is a tightly proper saddle point of Lagrange map  .
.
8. Conclusions
In this paper, we have extended the concept of tightly proper efficiency from normed linear spaces to locally convex topological vector spaces and got the equivalent relations among tightly proper efficiency, strict efficiency and superefficiency. We have also obtained a scalarization theorem and two Lagrange multiplier theorems for tightly proper efficiency in vector optimization involving nearly cone-subconvexlike set-valued maps. Then, we have introduced a Lagrange dual problem and got some duality results in terms of tightly properly efficient solutions. To characterize tightly proper efficiency, we have also introduced a new type of saddle point, which is called the tightly proper saddle point of an appropriate set-valued Lagrange map, and obtained its necessary and sufficient optimality conditions. Simultaneously, we have also given some examples to illustrate these concepts and results. On the other hand, by using the results of the Section 3 in this paper, we know that the above results hold for superefficiency and strict efficiency in vector optimization involving nearly cone-convexlike set-valued maps and, by virtue of [12, Theorem 3.11], all the above results also hold for positive proper efficiency, Hurwicz proper efficiency, global Henig proper efficiency and global Borwein proper efficiency in vector optimization with set-valued maps under the conditions that the set-valued  and
and  is closed convex and the ordering cone
is closed convex and the ordering cone  has a weakly compact base.
has a weakly compact base.
References
Kuhn HW, Tucker AW: Nonlinear programming. In Proceedings of the 2nd Berkeley Symposium on Mathematical Statistics and Probability, 1951, Berkeley, Calif, USA. University of California Press; 481–492.
Geoffrion AM: Proper efficiency and the theory of vector maximization. Journal of Mathematical Analysis and Applications 1968, 22: 618–630. 10.1016/0022-247X(68)90201-1
Borwein J: Proper efficient points for maximizations with respect to cones. SIAM Journal on Control and Optimization 1977,15(1):57–63. 10.1137/0315004
Hartley R: On cone-efficiency, cone-convexity and cone-compactness. SIAM Journal on Applied Mathematics 1978,34(2):211–222. 10.1137/0134018
Benson HP: An improved definition of proper efficiency for vector maximization with respect to cones. Journal of Mathematical Analysis and Applications 1979,71(1):232–241. 10.1016/0022-247X(79)90226-9
Henig MI: Proper efficiency with respect to cones. Journal of Optimization Theory and Applications 1982,36(3):387–407. 10.1007/BF00934353
Borwein JM, Zhuang D: Super efficiency in vector optimization. Transactions of the American Mathematical Society 1993,338(1):105–122. 10.2307/2154446
Fu WT: The strictly efficient points of a set in a normed linear space. Journal of Systems Science and Mathematical Sciences 1997,17(4):324–329.
Zaffaroni A: Degrees of efficiency and degrees of minimality. SIAM Journal on Control and Optimization 2003,42(3):1071–1086. 10.1137/S0363012902411532
Zheng XY: Proper efficiency in locally convex topological vector spaces. Journal of Optimization Theory and Applications 1997,94(2):469–486. 10.1023/A:1022648115446
Guerraggio A, Molho E, Zaffaroni A: On the notion of proper efficiency in vector optimization. Journal of Optimization Theory and Applications 1994,82(1):1–21. 10.1007/BF02191776
Liu J, Song W: On proper efficiencies in locally convex spaces—a survey. Acta Mathematica Vietnamica 2001,26(3):301–312.
Corley HW: Existence and Lagrangian duality for maximizations of set-valued functions. Journal of Optimization Theory and Applications 1987,54(3):489–501. 10.1007/BF00940198
Li Z-F, Chen G-Y: Lagrangian multipliers, saddle points, and duality in vector optimization of set-valued maps. Journal of Mathematical Analysis and Applications 1997,215(2):297–316. 10.1006/jmaa.1997.5568
Song W: Lagrangian duality for minimization of nonconvex multifunctions. Journal of Optimization Theory and Applications 1997,93(1):167–182. 10.1023/A:1022658019642
Chen GY, Jahn J: Optimality conditions for set-valued optimization problems. Mathematical Methods of Operations Research 1998,48(2):187–200. 10.1007/s001860050021
Rong WD, Wu YN: Characterizations of super efficiency in cone-convexlike vector optimization with set-valued maps. Mathematical Methods of Operations Research 1998,48(2):247–258. 10.1007/s001860050026
Li SJ, Yang XQ, Chen GY: Nonconvex vector optimization of set-valued mappings. Journal of Mathematical Analysis and Applications 2003,283(2):337–350. 10.1016/S0022-247X(02)00410-9
Gong X-H: Optimality conditions for Henig and globally proper efficient solutions with ordering cone has empty interior. Journal of Mathematical Analysis and Applications 2005,307(1):12–31. 10.1016/j.jmaa.2004.10.001
Sach PH: New generalized convexity notion for set-valued maps and application to vector optimization. Journal of Optimization Theory and Applications 2005,125(1):157–179. 10.1007/s10957-004-1716-4
Li ZF: Benson proper efficiency in the vector optimization of set-valued maps. Journal of Optimization Theory and Applications 1998,98(3):623–649. 10.1023/A:1022676013609
Mehra A: Super efficiency in vector optimization with nearly convexlike set-valued maps. Journal of Mathematical Analysis and Applications 2002,276(2):815–832. 10.1016/S0022-247X(02)00452-3
Xia LY, Qiu JH: Superefficiency in vector optimization with nearly subconvexlike set-valued maps. Journal of Optimization Theory and Applications 2008,136(1):125–137. 10.1007/s10957-007-9291-0
Kim DS, Lee GM, Sach PH: Hartley proper efficiency in multifunction optimization. Journal of Optimization Theory and Applications 2004,120(1):129–145.
Sach PH: Hartley proper efficiency in multiobjective optimization problems with locally Lipschitz set-valued objectives and constraints. Journal of Global Optimization 2006,35(1):1–25. 10.1007/s10898-005-1652-3
Huang XX, Yang XQ: On characterizations of proper efficiency for nonconvex multiobjective optimization. Journal of Global Optimization 2002,23(3–4):213–231.
Cheng YH, Fu WT: Strong efficiency in a locally convex space. Mathematical Methods of Operations Research 1999,50(3):373–384. 10.1007/s001860050076
Zhuang D: Density results for proper efficiencies. SIAM Journal on Control and Optimization 1994,32(1):51–58. 10.1137/S0363012989171518
Yang XM, Li D, Wang SY: Near-subconvexlikeness in vector optimization with set-valued functions. Journal of Optimization Theory and Applications 2001,110(2):413–427. 10.1023/A:1017535631418
Sach PH: Nearly subconvexlike set-valued maps and vector optimization problems. Journal of Optimization Theory and Applications 2003,119(2):335–356.
Acknowledgments
The authors would like to thank the anonymous referees for their valuable comments and suggestions, which helped to improve the paper. This research was partially supported by the National Natural Science Foundation of China (Grant no. 10871216) and the Fundamental Research Funds for the Central Universities (project no. CDJXS11102212).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Xu, Y., Li, S. Tightly Proper Efficiency in Vector Optimization with Nearly Cone-Subconvexlike Set-Valued Maps. J Inequal Appl 2011, 839679 (2011). https://doi.org/10.1155/2011/839679
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/839679
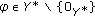 . Then
. Then 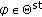 if and only if there exists a neighborhood
if and only if there exists a neighborhood  of
of 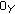 such that
such that 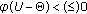 .
. is a bounded base of
is a bounded base of 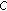 , then
, then  .
.



 such that
such that