- Research Article
- Open access
- Published:
On the Growth of Solutions of Some Second-Order Linear Differential Equations
Journal of Inequalities and Applications volume 2011, Article number: 635604 (2011)
Abstract
We investigate the growth of solutions of  , where
, where  and
and  are entire functions. When
are entire functions. When  and
and  satisfy some conditions, we prove that every nonzero solution of the above equation has infinite order and hyper-order 1, which improve the previous results.
satisfy some conditions, we prove that every nonzero solution of the above equation has infinite order and hyper-order 1, which improve the previous results.
1. Introduction and Results
In this paper, we willassume that the reader is familiar with the fundamental results and the standard notations of the Nevanlinna's value distribution theory of meromorphic functions (e.g., see [1–3]). In addition, we will use the notation  to denote the order of growth of meromorphic function
to denote the order of growth of meromorphic function  ,
,  to denote the hyper-order of
to denote the hyper-order of  (see [3]).
(see [3]).  is defined to be
is defined to be

We consider the second-order linear differential equation

where  and
and  are entire functions of finite order. It is well known that each solution of (1.2) is an entire function, and most solutions of (1.2) have infinite order.
are entire functions of finite order. It is well known that each solution of (1.2) is an entire function, and most solutions of (1.2) have infinite order.
Thus, a natural question is what conditions on  and
and  will guarantee that every solution
will guarantee that every solution  of (1.2) has infinite order? Ozawa [4], Gundersen [5], Amemiya and Ozawa [6], and Langley [7] have studied the problem with
of (1.2) has infinite order? Ozawa [4], Gundersen [5], Amemiya and Ozawa [6], and Langley [7] have studied the problem with  and
and  is complex number or polynomial. For the case that
is complex number or polynomial. For the case that  , and
, and  is transcendental entire function, Gundersen proved the following in [5, Theorem A].
is transcendental entire function, Gundersen proved the following in [5, Theorem A].
Theorem A.
If  is a transcendental entire function with order
is a transcendental entire function with order  , then every solution
, then every solution  of equation
of equation

has infinite order.
Theorem A states that when  , (1.3) may have finite-order solutions. We go deep into the problem: what condition in
, (1.3) may have finite-order solutions. We go deep into the problem: what condition in  when
when  will guarantee every solution
will guarantee every solution  of (1.3) has infinite order? And more precise estimation for its rate of growth is a very important aspect. Chen investigated the problem and obtain the following in [8, Theorem B and Theorem C].
of (1.3) has infinite order? And more precise estimation for its rate of growth is a very important aspect. Chen investigated the problem and obtain the following in [8, Theorem B and Theorem C].
Theorem B.
Let 

 be entire functions with
be entire functions with  be complex numbers such that
be complex numbers such that  and
and  . then every solution
. then every solution  of the equation
of the equation

has infinite order.
Theorem C.
Let  be nonzero complex numbers and
be nonzero complex numbers and  be a nonconstant polynomial or
be a nonconstant polynomial or  where
where  is nonzero polynomial, then every solution
is nonzero polynomial, then every solution  of the equation
of the equation

has infinite order and  .
.
For Theorems B and C, many authors, Wang and Lü [9],Huang, Chen, and Li [10], and Cheng and Kang [11] have made some improvement. In this paper, we areconcerned with the more general problem, and obtain the following theorem that extend and improve the previous results.
Theorem 1.1.
Let  be entire functions with
be entire functions with  be complex numbers such that
be complex numbers such that  (suppose that
(suppose that  . If
. If  or
or  , then every solution
, then every solution  of the equation
of the equation

has infinite order and  .
.
2. Remarks and Lemmas for the Proof of Theorem
Lemma 2.1 (see [12]).
Let  be a transcendental meromorphic function with
be a transcendental meromorphic function with  be a finite set of distinct pairs of integers satisfying
be a finite set of distinct pairs of integers satisfying  . And let
. And let  be a given constant. Then,
be a given constant. Then,
(i)there exists a set  with linear measure zero, such that, if
with linear measure zero, such that, if  , then there is a constant
, then there is a constant  , such that for all
, such that for all  satisfying
satisfying  and
and  and for all
and for all  , one has
, one has

(ii)there exists a set  with finite logarithmic measure, such that for all
with finite logarithmic measure, such that for all  satisfying
satisfying  and for all
and for all  , we have
, we have

(iii)there exists a set  with finite linear measure, such that for all
with finite linear measure, such that for all  satisfying
satisfying  and for all
and for all  , we have
, we have

Lemma 2.2 (see [8]).
Suppose that  are real numbers,
are real numbers,  is a polynomial with degree
is a polynomial with degree  , that
, that  is an entire function with
is an entire function with  . Set
. Set  . Then for any given
. Then for any given  , there exists a set
, there exists a set  that has the linear measure zero, such that for any
that has the linear measure zero, such that for any  , there is
, there is  , such that for
, such that for  , we have
, we have
(i)if  , then
, then

(ii)if  , then
, then

where  is a finite set.
is a finite set.
Using Lemma 2.2, we can prove Lemma 2.3.
Lemma 2.3.
Suppose that  is a positive entire number. Let
is a positive entire number. Let  be nonconstant polynomials, where
be nonconstant polynomials, where  are complex numbers and
are complex numbers and  . Set
. Set  , then there is a set
, then there is a set  that has linear measure zero. If
that has linear measure zero. If  , then there exists a ray
, then there exists a ray  ,
,  , such that
, such that

or

where  is a finite set, which has linear measure zero.
is a finite set, which has linear measure zero.
Proof.
According to the values of  and
and  , we divide our discussion into three cases.
, we divide our discussion into three cases.
Case 1 ( ).
).
-
(a)
If
 , let
, let 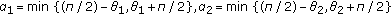 , Then there are three cases: (i)
, Then there are three cases: (i)  ; (ii)
; (ii) 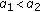 ; (iii)
; (iii)  .
. -
(i)
 . By
. By 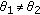 , we know that
, we know that 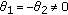 .
.
Suppose that  , then take
, then take  is any constant in
is any constant in  .
.
Since  has linear measure zero, there exists
has linear measure zero, there exists  such that
such that  . Thus
. Thus  . By
. By  and
and  that is
that is  , we have
, we have

Therefore,

When  , then
, then  , we can prove it by using similar argument action as in the above proof.
, we can prove it by using similar argument action as in the above proof.
-
(ii)
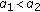 , then
, then 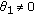 . Suppose that
. Suppose that 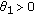 , then
, then 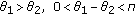 . Let
. Let  , and take
, and take 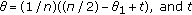 is any constant in
is any constant in  .
.
Since  has a linear measure zero, there exists
has a linear measure zero, there exists  such that
such that  ,
,

Therefore

Suppose that  , then
, then  . Let
. Let  , and take
, and take  is any constant in
is any constant in  .
.
Since  has linear measure zero, there exists
has linear measure zero, there exists  such that
such that  ,
,

Therefore,

-
(iii)
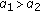 , then
, then 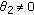 . Using similar method as in proof of (ii), we know that there exists
. Using similar method as in proof of (ii), we know that there exists  such that
such that 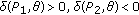 .
. -
(b)
When
 , we can prove it by using the same argument action as in (a).
, we can prove it by using the same argument action as in (a). -
(c)
When
 , we just prove the case that
, we just prove the case that  (when
(when 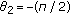 , we can prove it by using the same reasoning).
, we can prove it by using the same reasoning).
Let  , take
, take  is any constant in
is any constant in  .
.
Since  has a linear measure zero, there exists
has a linear measure zero, there exists  , such that
, such that  . Then
. Then

When  ,
,  , thus,
, thus,  .
.
When  ,
,  , thus,
, thus,  .
.
Therefore

Case 2.
When  , or
, or  and
and  , using a proof similar to Case 1, we can get the conclusion.
, using a proof similar to Case 1, we can get the conclusion.
Case 3 ( and
and  ).
).
By  , there are only two cases:
, there are only two cases:  ; or
; or  .
.
If  . Take
. Take  is any constant in
is any constant in  .
.
Since  has linear measure zero, there exists
has linear measure zero, there exists  such that
such that  . Using a proof similar to Case 1(c), we can prove it.
. Using a proof similar to Case 1(c), we can prove it.
When  , we can prove it by using the same reasoning
, we can prove it by using the same reasoning
Remark 2.4.
Using the similar reasoning of Lemma 2.3, we can obtain that, in Lemma 2.3, if  is replaced by
is replaced by  , then it has the same result.
, then it has the same result.
Lemma 2.5 (see [8]).
Let  be entire functions with finite order. If
be entire functions with finite order. If  is a solution of the equation
is a solution of the equation

then  .
.
Lemma 2.6 (see [12]).
Let  be a transcendental meromorphic function, and let
be a transcendental meromorphic function, and let  be a given constant, Then there exists a set
be a given constant, Then there exists a set  with finite logarithmic measure and a constant
with finite logarithmic measure and a constant  that depends only on
that depends only on  and
and  (
(  ), such that for all
), such that for all  satisfying
satisfying  ,
,

Remark 2.7.
In Lemma 2.6, when  , we have
, we have

Lemma 2.8 (see [13]).
Suppose that  and
and  are nondecreasing functions, such that
are nondecreasing functions, such that  , where
, where  is a set with at most finite measure, then for any constant
is a set with at most finite measure, then for any constant  , there exists
, there exists  such that
such that  for all
for all  .
.
3. Proof of Theorem 1.1
Suppose that  is a solution of (1.6), then,
is a solution of (1.6), then,  is an entire function.
is an entire function.
First Step
We prove that  . Suppose, to the contrary, that
. Suppose, to the contrary, that  . By Lemma 2.1, for any given
. By Lemma 2.1, for any given  , there exists a set
, there exists a set  of linear measure zero, such that if
of linear measure zero, such that if  , then, there is a constant
, then, there is a constant  , such that for all
, such that for all  satisfying
satisfying  and
and  , we have
, we have

Let  .
.
Case 1 ( , which is
, which is  ).
).
-
(i)
Suppose that
 . By Lemmas 2.2 and 2.3, for the above
. By Lemmas 2.2 and 2.3, for the above  , there is a ray
, there is a ray  , such that
, such that 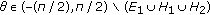 (where
(where 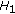 and
and  are defined as in Lemma 2.3, and
are defined as in Lemma 2.3, and 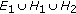 is of the linear measure zero), and satisfying
is of the linear measure zero), and satisfying  (3.2)
(3.2)
or

When  , for sufficiently large
, for sufficiently large  , we have
, we have

Hence

By (1.6), we obtain

Since  , we know that
, we know that  , then
, then  . Substituting (3.1) and (3.5) into (3.6), we get
. Substituting (3.1) and (3.5) into (3.6), we get

By  , we know that (3.7) is a contradiction.
, we know that (3.7) is a contradiction.
When  , using a proof similar to the above, we can also get a contradiction.
, using a proof similar to the above, we can also get a contradiction.
-
(ii)
Suppose that
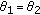 . By Lemma 2.2, for the above
. By Lemma 2.2, for the above  , there is a ray
, there is a ray 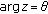 such that
such that 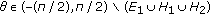 and
and 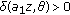 . Since
. Since 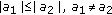 , and
, and 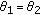 , then
, then 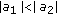 , thus
, thus 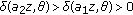 . For sufficiently large
. For sufficiently large  , we have
, we have  (3.8)
(3.8)
Hence,

where  .
.
Since  , we see that
, we see that  , then
, then  .
.
Since  , we know that
, we know that  , then
, then  . Substituting (3.1) and (3.9) into (3.6), we obtain
. Substituting (3.1) and (3.9) into (3.6), we obtain

Since  , we know that (3.10) is a contradiction.
, we know that (3.10) is a contradiction.
Case 2 ( , which is
, which is  ).
).
-
(i)
Suppose that
 , then
, then 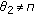 . By Lemma 2.2, for the above
. By Lemma 2.2, for the above  , there is a ray
, there is a ray  such that
such that 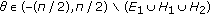 and
and 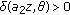 . Because
. Because  . For sufficiently large
. For sufficiently large  , we have
, we have 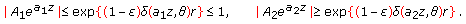 (3.11)
(3.11)
Hence

Using the same reasoning as in Case 1(i), we can get a contradiction.
-
(ii)
Suppose that
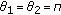 . By Lemma 2.2, for the above
. By Lemma 2.2, for the above  , there is a ray
, there is a ray 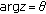 such that
such that 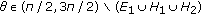 , then
, then 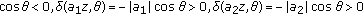 , Since
, Since  and
and 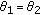 , then
, then  . Thus,
. Thus,  , for sufficiently large
, for sufficiently large  , we get that (3.8) and (3.9) hold.
, we get that (3.8) and (3.9) hold.
Since  , then
, then  .
.
Using the same reasoning as in Case 1(ii), we can get a contradiction.
Concluding the above proof, we obtain  .
.
Second Step
We prove that  .
.
By Lemma 2.5 and  , then
, then  .
.
By Lemma 2.6 and Remark 2.7, we know that there exists a set  with finite logarithmic measure and a constant
with finite logarithmic measure and a constant  , such that for all
, such that for all  satisfying
satisfying  , we get that (2.18) holds.
, we get that (2.18) holds.
For Cases 1 and 2(i) in first step, we have proved that there is a ray  satisfying
satisfying  , for sufficiently large
, for sufficiently large  , we get that (3.5) or (3.9) or (3.12) hold, that is,
, we get that (3.5) or (3.9) or (3.12) hold, that is,

where  is a constant.
is a constant.
Since  , then
, then  . By (2.18), (3.6), and (3.13), we obtain
. By (2.18), (3.6), and (3.13), we obtain

By  , (3.14) and Lemma 2.8, we know that there exists
, (3.14) and Lemma 2.8, we know that there exists  , when
, when  , we have
, we have  , then
, then  .
.
For Case 2(ii) in first step, we have proved that there is a ray  satisfying
satisfying  , for sufficiently large
, for sufficiently large  , we get (3.9) hold, and we also get that
, we get (3.9) hold, and we also get that  .
.
By (2.18), (3.6), and (3.9), we obtain

By  and (3.15) and Lemma 2.8, we know that there exists
and (3.15) and Lemma 2.8, we know that there exists  , when
, when  , we have
, we have  , then
, then  .
.
Concluding the above proof, we obtain  .
.
Theorem 1.1 is thus proved.
References
Hayman WK: Meromorphic Functions, Oxford Mathematical Monographs. Clarendon Press, Oxford, UK; 1964:xiv+191.
Yang L: Value Distribution Theory. Science Press, Beijing, China; 1993:xii+269.
Yang C-C, Yi H-X: Uniqueness Theory of Meromorphic Functions, Mathematics and Its Applications. Volume 557. Kluwer Academic Publishers Group, Dordrecht, The Netherlands; 2003:viii+569.
Ozawa M: On a solution of . Kodai Mathematical Journal 1980,3(2):295–309. 10.2996/kmj/1138036197
Gundersen GG: On the question of whether can admit a solution of finite order. Proceedings of the Royal Society of Edinburgh A 1986,102(1–2):9–17. 10.1017/S0308210500014451
Amemiya I, Ozawa M: Non-existence of finite order solutions of . Hokkaido Mathematical Journal 1981, 10: 1–17.
Langley JK: On complex oscillation and a problem of Ozawa. Kodai Mathematical Journal 1986,9(3):430–439. 10.2996/kmj/1138037272
Chen ZX: The growth of solutions of where the order . Science in China A 2002,45(3):290–300.
Wang J, Lü WR: The fixed points and hyper-order of solutions of second order linear differential equations with meromorphic coefficients. Acta Mathematicae Applicatae Sinica 2004,27(1):72–80.
Huang Z-B, Chen Z-X, Li Q: Subnormal solutions of second-order nonhomogeneous linear differential equations with periodic coefficients. Journal of Inequalities and Applications 2009, 2009: 1–12.
Cheng T, Kang Y-M: The growth of the solution of a certain linear differential equation. Journal of Fudan University: Natural Science 2006,45(5):611–618.
Gundersen GG: Estimates for the logarithmic derivative of a meromorphic function, plus similar estimates. Journal of the London Mathematical Society 1988,37(1):88–104.
Hayman WK: The local growth of power series: a survey of the Wiman-Valiron method. Canadian Mathematical Bulletin 1974,17(3):317–358. 10.4153/CMB-1974-064-0
Acknowledgment
This project was supported by the National Natural Science Foundation of China (no. 10871076).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Peng, F., Chen, ZX. On the Growth of Solutions of Some Second-Order Linear Differential Equations. J Inequal Appl 2011, 635604 (2011). https://doi.org/10.1155/2011/635604
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/635604
 , let
, let 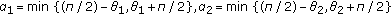 , Then there are three cases: (i)
, Then there are three cases: (i)  ; (ii)
; (ii) 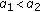 ; (iii)
; (iii)  .
. . By
. By 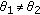 , we know that
, we know that 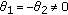 .
.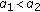 , then
, then 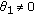 . Suppose that
. Suppose that 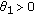 , then
, then 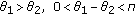 . Let
. Let  , and take
, and take 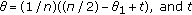 is any constant in
is any constant in  .
.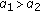 , then
, then 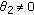 . Using similar method as in proof of (ii), we know that there exists
. Using similar method as in proof of (ii), we know that there exists  such that
such that 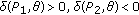 .
. , we can prove it by using the same argument action as in (a).
, we can prove it by using the same argument action as in (a). , we just prove the case that
, we just prove the case that  (when
(when 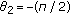 , we can prove it by using the same reasoning).
, we can prove it by using the same reasoning). . By Lemmas 2.2 and 2.3, for the above
. By Lemmas 2.2 and 2.3, for the above  , there is a ray
, there is a ray  , such that
, such that 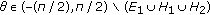 (where
(where 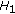 and
and  are defined as in Lemma 2.3, and
are defined as in Lemma 2.3, and 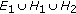 is of the linear measure zero), and satisfying
is of the linear measure zero), and satisfying 
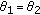 . By Lemma 2.2, for the above
. By Lemma 2.2, for the above  , there is a ray
, there is a ray 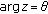 such that
such that 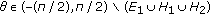 and
and 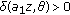 . Since
. Since 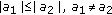 , and
, and 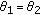 , then
, then 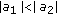 , thus
, thus 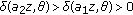 . For sufficiently large
. For sufficiently large  , we have
, we have 
 , then
, then 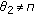 . By Lemma 2.2, for the above
. By Lemma 2.2, for the above  , there is a ray
, there is a ray  such that
such that 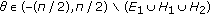 and
and 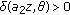 . Because
. Because  . For sufficiently large
. For sufficiently large  , we have
, we have 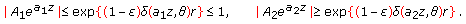
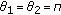 . By Lemma 2.2, for the above
. By Lemma 2.2, for the above  , there is a ray
, there is a ray 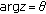 such that
such that 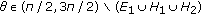 , then
, then 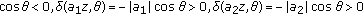 , Since
, Since  and
and 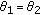 , then
, then  . Thus,
. Thus,  , for sufficiently large
, for sufficiently large  , we get that (3.8) and (3.9) hold.
, we get that (3.8) and (3.9) hold.