- Research Article
- Open access
- Published:
Some New Double Sequence Spaces Defined by Orlicz Function in  -Normed Space
-Normed Space
Journal of Inequalities and Applications volume 2011, Article number: 592840 (2011)
Abstract
The aim of this paper is to introduce and study some new double sequence spaces with respect to an Orlicz function, and also some properties of the resulting sequence spaces were examined.
1. Introduction
We recall that the concept of a 2-normed space was first given in the works of Gähler ([1, 2]) as an interesting nonlinear generalization of a normed linear space which was subsequently studied by many authors (see, [3, 4]). Recently, a lot of activities have started to study summability, sequence spaces, and related topics in these nonlinear spaces (see, e.g., [5–9]). In particular, Savaş [10] combined Orlicz function and ideal convergence to define some sequence spaces using 2-norm.
In this paper, we introduce and study some new double-sequence spaces, whose elements are form  -normed spaces, using an Orlicz function, which may be considered as an extension of various sequence spaces to
-normed spaces, using an Orlicz function, which may be considered as an extension of various sequence spaces to  -normed spaces. We begin with recalling some notations and backgrounds.
-normed spaces. We begin with recalling some notations and backgrounds.
Recall in [11] that an Orlicz function  is continuous, convex, and nondecreasing function such that
is continuous, convex, and nondecreasing function such that  and
and  for
for  , and
, and  as
as  .
.
Subsequently, Orlicz function was used to define sequence spaces by Parashar and Choudhary [12] and others. An Orlicz function  can always be represented in the following integral form:
can always be represented in the following integral form:  , where
, where  is the known kernel of
is the known kernel of  , right differential for
, right differential for  ,
,  ,
,  for
for  ,
,  is nondecreasing, and
is nondecreasing, and  as
as  .
.
If convexity of Orlicz function  is replaced by
is replaced by  , then this function is called Modulus function, which was presented and discussed by Ruckle [13] and Maddox [14].
, then this function is called Modulus function, which was presented and discussed by Ruckle [13] and Maddox [14].
Remark 1.1.
If  is a convex function and
is a convex function and  , then
, then  for all
for all  with
with  .
.
Let  and
and  be real vector space of dimension
be real vector space of dimension  , where
, where  . An
. An  -norm on
-norm on  is a function
is a function  which satisfies the following four conditions:
which satisfies the following four conditions:
(i) if and only if
if and only if  are linearly dependent,
are linearly dependent,
(ii) are invariant under permutation,
are invariant under permutation,
(iii) ,
,  ,
,
(iv) .
.
The pair  is then called an
is then called an  -normed space [3].
-normed space [3].
Let  be equipped with the
be equipped with the  -norm, then
-norm, then  the volume of the
the volume of the  -dimensional parallelepiped spanned by the vectors,
-dimensional parallelepiped spanned by the vectors,  which may be given explicitly by the formula
which may be given explicitly by the formula

where  denotes inner product. Let
denotes inner product. Let  be an
be an  -normed space of dimension
-normed space of dimension  and
and  a linearly independent set in
a linearly independent set in  . Then, the function
. Then, the function  on
on  is defined by
is defined by

is defines an  norm on
norm on  with respect to
with respect to  (see, [15]).
(see, [15]).
Definition 1.2 (see [7]).
A sequence  in
in  -normed space
-normed space  is aid to be convergent to an
is aid to be convergent to an  in
in  (in the
(in the  -norm) if
-norm) if

for every  .
.
Definition 1.3 (see [16]).
Let  be a linear space. Then, a map
be a linear space. Then, a map  is called a paranorm (on
is called a paranorm (on  ) if it is satisfies the following conditions for all
) if it is satisfies the following conditions for all  and
and  scalar:
scalar:
(i)
 ,
,
(ii) ,
,
(iii) ,
,
(iv) and
and  imply
imply  .
.
2. Main Results
Let  be any
be any  -normed space, and let
-normed space, and let  denote
denote  -valued sequence spaces. Clearly
-valued sequence spaces. Clearly  is a linear space under addition and scalar multiplication.
is a linear space under addition and scalar multiplication.
Definition 2.1.
Let  be an Orlicz function and
be an Orlicz function and  any
any  -normed space. Further, let
-normed space. Further, let  be a bounded sequence of positive real numbers. Now, we define the following new double sequence space as follows:
be a bounded sequence of positive real numbers. Now, we define the following new double sequence space as follows:

for each  .
.
The following inequalities will be used throughout the paper. Let  be a double sequence of positive real numbers with
be a double sequence of positive real numbers with  , and let
, and let  . Then, for the factorable sequences
. Then, for the factorable sequences  and
and  in the complex plane, we have as in Maddox [16]
in the complex plane, we have as in Maddox [16]

Theorem 2.2.
 sequences space is a linear space.
sequences space is a linear space.
Proof.
Now, assume that  and
and  . Then,
. Then,

Since  is a
is a  -norm on
-norm on  , and
, and  is an Orlicz function, we get
is an Orlicz function, we get

where

and this completes the proof.
Theorem 2.3.
 space is a paranormed space with the paranorm defined by
space is a paranormed space with the paranorm defined by 

where  ,
,  .
.
Proof.
-
(i)
Clearly,
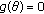 and (ii)
and (ii) 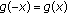 . (iii) Let
. (iii) Let 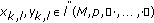 , then there exists
, then there exists 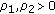 such that
such that 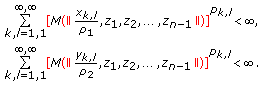 (2.7)
(2.7)
So, we have

and thus

-
(iv)
Now, let
 and
and 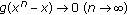 . Since
. Since 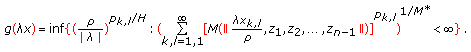 (2.10)
(2.10)
This gives us  .
.
Theorem 2.4.
If  for each
for each  and
and  , then
, then  .
.
Proof.
If  , then there exists some
, then there exists some  such that
such that

This implies that

for sufficiently large values of  and
and  . Since
. Since  is nondecreasing, we are granted
is nondecreasing, we are granted

Thus,  . This completes the proof.
. This completes the proof.
The following result is a consequence of the above theorem.
Corollary 2.5.
-
(i)
If
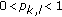 for each
for each 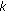 and
and  , then
, then 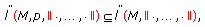 (2.14)
(2.14)
-
(ii)
If
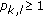 for each
for each 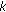 and
and  , then
, then 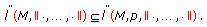 (2.15)
(2.15)
Theorem 2.6.
 , where
, where  is the double space of bounded sequences and
is the double space of bounded sequences and  .
.
Proof.
 . Then, there exists an
. Then, there exists an  such that
such that  for each
for each  ,
,  . We want to show
. We want to show 
 . But
. But

and this completes the proof.
Theorem 2.7.
Let  and
and  be Orlicz function. Then, we have
be Orlicz function. Then, we have

Proof.
We have

Let  ; when adding the above inequality from
; when adding the above inequality from  to
to  we get
we get  and this completes the proof.
and this completes the proof.
Definition 2.8 (see [10]).
Let  be a sequence space. Then,
be a sequence space. Then,  is called solid if
is called solid if  whenever
whenever  for all sequences
for all sequences  of scalars with
of scalars with  for all
for all  .
.
Definition 2.9.
Let  be a sequence space. Then,
be a sequence space. Then,  is called monotone if it contains the canonical preimages of all its step spaces (see, [17]).
is called monotone if it contains the canonical preimages of all its step spaces (see, [17]).
Theorem 2.10.
The sequence space  is solid.
is solid.
Proof.
Let  ; that is,
; that is,

Let ( ) be double sequence of scalars such that
) be double sequence of scalars such that  for all
for all  . Then, the result follows from the following inequality:
. Then, the result follows from the following inequality:

and this completes the proof.
We have the following result in view of Remark 1.1 and Theorem 2.10.
Corollary 2.11.
The sequence space  is monotone.
is monotone.
Definition 2.12 (see [18]).
Let  denote a four-dimensional summability method that maps the complex double sequences
denote a four-dimensional summability method that maps the complex double sequences  into the double-sequence
into the double-sequence  , where the
, where the  th term to
th term to  is as follows:
is as follows:

Such transformation is said to be nonnegative if  is nonnegative for all
is nonnegative for all  , and
, and  .
.
Definition 2.13.
Let  be a nonnegative matrix. Let
be a nonnegative matrix. Let  be an Orlicz function and
be an Orlicz function and  a factorable double sequence of strictly positive real numbers. Then, we define the following sequence spaces:
a factorable double sequence of strictly positive real numbers. Then, we define the following sequence spaces:

for each  . If
. If  , then we say
, then we say  is
is  summable to
summable to  , where
, where  .
.
If we take  and
and  for all
for all  , then we have
, then we have

Theorem 2.14.
 is linear spaces.
is linear spaces.
Proof.
This can be proved by using the techniques similar to those used in Theorem 2.2.
Theorem 2.15.
-
(1)
If
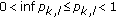 , then
, then 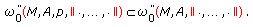 (2.24)
(2.24)
-
(2)
If
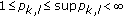 , then
, then 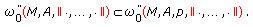 (2.25)
(2.25)
Proof.
-
(1)
Let
 ; since
; since  , we have
, we have 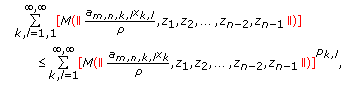 (2.26)
(2.26)
and hence  .
.
-
(2)
Let
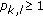 for each
for each  and
and  . Let
. Let  .
.
Then, for each  , there exists a positive integer
, there exists a positive integer  such that
such that

for all  . This implies that
. This implies that

Thus,  , and this completes the proof.
, and this completes the proof.
References
Gähler S: Lineare 2-normierte Räume. Mathematische Nachrichten 1965, 28: 1–43.
Gähler S: Über die Uniformisierbarkeit 2-metrischer Räume. Mathematische Nachrichten 1965, 28: 235–244.
Gunawan H: The space of -summable sequences and its natural -norm. Bulletin of the Australian Mathematical Society 2001,64(1):137–147. 10.1017/S0004972700019754
Freese RW, Cho YJ: Geometry of Linear 2-Normed Spaces. Nova Science Publishers, Hauppauge, NY, USA; 2001:viii+301.
Şahiner A, Gürdal M, Saltan S, Gunawan H: Ideal convergence in 2-normed spaces. Taiwanese Journal of Mathematics 2007,11(5):1477–1484.
Gürdal M, Pehlivan S: Statistical convergence in 2-normed spaces. Southeast Asian Bulletin of Mathematics 2009,33(2):257–264.
Gunawan H, Mashadi M: On -normed spaces. International Journal of Mathematics and Mathematical Sciences 2001,27(10):631–639. 10.1155/S0161171201010675
Sahiner A, Gurdal M: New sequence spaces in -normed spaces with respect to an Orlicz function. The Aligarh Bulletin of Mathematics 2008,27(1):53–58.
Savaş E: On some new sequence spaces in 2-normed spaces using ideal convergence and an Orlicz function. journal of Inequalities and Applications 2010, 2010:-8. Article ID 482392
Savaş E: -strongly summable sequences spaces in 2-normed spaces defined by ideal convergence and an Orlicz function. Applied Mathematics and Computation 2010,217(1):271–276. 10.1016/j.amc.2010.05.057
Krasnoselski MA, Rutisky YB: Convex Function and Orlicz Spaces. Noordhoff, Groningen, The Netherlands; 1961.
Parashar SD, Choudhary B: Sequence spaces defined by Orlicz functions. Indian Journal of Pure and Applied Mathematics 1994,25(4):419–428.
Ruckle WH: spaces in which the sequence of coordinate vectors is bounded. Canadian Journal of Mathematics. Journal Canadien de Mathématiques 1973, 25: 973–978.
Maddox IJ: Sequence spaces defined by a modulus. Mathematical Proceedings of the Cambridge Philosophical Society 1986,100(1):161–166. 10.1017/S0305004100065968
Gunawan H: On -inner products, -norms, and the Cauchy-Schwarz inequality. Scientiae Mathematicae Japonicae 2002,55(1):53–60.
Maddox IJ: Elements of Functional Analysis. Cambridge University Press, London, UK; 1970:x+208.
Kampthan PK, Gupta M: Sequence Spaces and Series, Lecture Notes in Pure and Applied Mmathematics. Volume 65. Marcel Dekker, New York, NY, USA; 1981.
Savas E, Patterson RF: On some double sequence spaces defined by a modulus. Math. Slovaca 2011,61(2):1–12.
Acknowledgments
The author wishes to thank the referees for their careful reading of the paper and for their helpful suggestions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Savaş, E. Some New Double Sequence Spaces Defined by Orlicz Function in  -Normed Space.
J Inequal Appl 2011, 592840 (2011). https://doi.org/10.1155/2011/592840
-Normed Space.
J Inequal Appl 2011, 592840 (2011). https://doi.org/10.1155/2011/592840
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/592840
 and (ii)
and (ii) 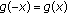 . (iii) Let
. (iii) Let 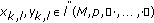 , then there exists
, then there exists 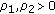 such that
such that 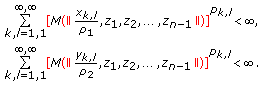
 and
and 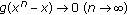 . Since
. Since 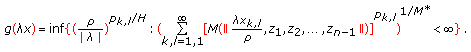
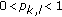 for each
for each 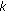 and
and  , then
, then 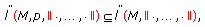
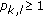 for each
for each  and
and  , then
, then 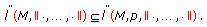
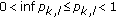 , then
, then 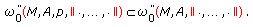
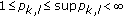 , then
, then 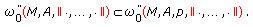
 ; since
; since  , we have
, we have 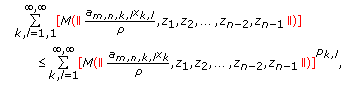
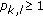 for each
for each  and
and  . Let
. Let  .
.