- Research Article
- Open access
- Published:
Bessel and Grüss Type Inequalities in Inner Product Modules over Banach  -Algebras
-Algebras
Journal of Inequalities and Applications volume 2011, Article number: 562923 (2011)
Abstract
We give an analogue of the Bessel inequality and we state a simple formulation of the Grüss type inequality in inner product  -modules, which is a refinement of it. We obtain some further generalization of the Grüss type inequalities in inner product modules over proper
-modules, which is a refinement of it. We obtain some further generalization of the Grüss type inequalities in inner product modules over proper  -algebras and unital Banach
-algebras and unital Banach  -algebras for
-algebras for  -seminorms and positive linear functionals.
-seminorms and positive linear functionals.
1. Introduction
A proper  -algebra is a complex Banach
-algebra is a complex Banach  -algebra
-algebra  where the underlying Banach space is a Hilbert space with respect to the inner product
where the underlying Banach space is a Hilbert space with respect to the inner product  satisfying the properties
satisfying the properties  and
and  for all
for all  . A
. A  -algebra is a complex Banach
-algebra is a complex Banach  -algebra
-algebra  such that
such that  for every
for every  . If
. If  is a proper
is a proper  -algebra or a
-algebra or a  -algebra and
-algebra and  is such that
is such that  or
or  , then
, then  .
.
For a proper  -algebra
-algebra  , the trace class associated with
, the trace class associated with  is
is  . For every positive
. For every positive  there exists the square root of
there exists the square root of  , that is, a unique positive
, that is, a unique positive  such that
such that  , the square root of
, the square root of  is denoted by
is denoted by  . There are a positive linear functional
. There are a positive linear functional  on
on  and a norm
and a norm  on
on  , related to the norm of A by the equality
, related to the norm of A by the equality  for every
for every  .
.
Let  be a proper
be a proper  -algebra or a
-algebra or a  -algebra. A semi-inner product module over
-algebra. A semi-inner product module over  is a right module
is a right module  over
over  together with a generalized semi-inner product, that is with a mapping
together with a generalized semi-inner product, that is with a mapping  on
on  , which is
, which is  -valued if
-valued if  is a proper
is a proper  -algebra, or
-algebra, or  -valued if
-valued if  is a
is a  -algebra, having the following properties:
-algebra, having the following properties:
(i) for all
for all  ,
,
(ii) for
for  ,
,  ,
,
(iii) for all
for all  ,
,
(iv) for
for  .
.
We will say that  is a semi-inner product
is a semi-inner product  -module if
-module if  is a proper
is a proper  -algebra and that
-algebra and that  is a semi-inner product
is a semi-inner product  -module if
-module if  is a
is a  -algebra.
-algebra.
If, in addition,
(v) implies
implies  ,
,
then  is called an inner product module over
is called an inner product module over  . The absolute value of
. The absolute value of  is defined as the square root of
is defined as the square root of  and it is denoted by
and it is denoted by  .
.
Let  be a
be a  -algebra. A seminorm
-algebra. A seminorm  on
on  is a real-valued function on
is a real-valued function on  such that for
such that for  and
and  :
:  ,
,  ,
,  . A seminorm
. A seminorm  on
on  is called a
is called a  -seminorm if it satisfies the
-seminorm if it satisfies the  -condition:
-condition:  . By Sebestyen's theorem [1, Theorem 38.1] every
. By Sebestyen's theorem [1, Theorem 38.1] every  -seminorm
-seminorm  on a
on a  -algebra
-algebra  is submultiplicative, that is,
is submultiplicative, that is,  , and by [2, Section 39, Lemma 2(i)]
, and by [2, Section 39, Lemma 2(i)]  . For every
. For every  , the spectral radius of
, the spectral radius of  is defined to be
is defined to be  .
.
The Pták function  on
on  -algebra
-algebra  is defined to be
is defined to be  , where
, where  . This function has important roles in Banach
. This function has important roles in Banach  -algebras, for example, on
-algebras, for example, on  -algebras,
-algebras,  is equal to the norm and on Hermitian Banach
is equal to the norm and on Hermitian Banach  -algebras
-algebras  is the greatest
is the greatest  -seminorm. By utilizing properties of the spectral radius and the Pták function, Pták [3] showed in 1970 that an elegant theory for Banach
-seminorm. By utilizing properties of the spectral radius and the Pták function, Pták [3] showed in 1970 that an elegant theory for Banach  -algebras arises from the inequality
-algebras arises from the inequality  .
.
This inequality characterizes Hermitian (and symmetric) Banach  -algebras, and further characterizations of
-algebras, and further characterizations of  -algebras follow as a result of Pták theory.
-algebras follow as a result of Pták theory.
Let  be a
be a  -algebra. We define
-algebra. We define  by
by

and call the elements of  positive.
positive.
The set  of positive elements is obviously a convex cone (i.e., it is closed under convex combinations and multiplication by positive constants). Hence we call
of positive elements is obviously a convex cone (i.e., it is closed under convex combinations and multiplication by positive constants). Hence we call  the positive cone. By definition, zero belongs to
the positive cone. By definition, zero belongs to  . It is also clear that each positive element is Hermitian.
. It is also clear that each positive element is Hermitian.
We recall that a Banach  -algebra
-algebra  is said to be an
is said to be an  -algebra provided there exists on
-algebra provided there exists on  a second norm
a second norm  , not necessarily complete, which is a
, not necessarily complete, which is a  -norm. The second norm will be called an auxiliary norm.
-norm. The second norm will be called an auxiliary norm.
Definition 1.1.
Let  be a
be a  -algebra. A semi-inner product
-algebra. A semi-inner product  -module (or semi-inner product
-module (or semi-inner product  -module) is a complex vector space which is also a right
-module) is a complex vector space which is also a right  -module
-module  with a sesquilinear semi-inner product
with a sesquilinear semi-inner product  , fulfilling
, fulfilling

for  ,
,  . Furthermore, if
. Furthermore, if  satisfies the strict positivity condition
satisfies the strict positivity condition

then  is called an inner product
is called an inner product  -module (or inner product
-module (or inner product  -module).
-module).
Let  be a seminorm or a positive linear functional on
be a seminorm or a positive linear functional on  and
and  . If
. If  is a seminorm on a semi-inner product
is a seminorm on a semi-inner product  -module
-module  , then
, then  is said to be a semi-Hilbert
is said to be a semi-Hilbert  -module.
-module.
If  is a norm on an inner product
is a norm on an inner product  -module
-module  , then
, then  is said to be a pre-Hilbert
is said to be a pre-Hilbert  -module.
-module.
A pre-Hilbert  -module which is complete with respect to its norm is called a Hilbert
-module which is complete with respect to its norm is called a Hilbert  -module.
-module.
Since  and
and  are self adjoint, therefore we get the following Corollary.
are self adjoint, therefore we get the following Corollary.
Corollary 1.2.
If  is a semi-inner product
is a semi-inner product  -module, then the following symmetry condition holds:
-module, then the following symmetry condition holds:

Example 1.3.
-
(a)
Let
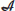 be a
be a  -algebra and
-algebra and  a positive linear functional or a
a positive linear functional or a  -seminorm on
-seminorm on  . It is known that
. It is known that 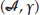 is a semi-Hilbert
is a semi-Hilbert 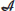 -module over itself with the inner product defined by
-module over itself with the inner product defined by 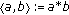 , in this case
, in this case  .
. -
(b)
Let
 be a Hermitian Banach
be a Hermitian Banach  -algebra and
-algebra and  be the Pták function on
be the Pták function on 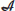 . If
. If 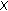 is a semi-inner product
is a semi-inner product 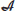 -module and
-module and 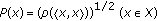 , then
, then  is a semi-Hilbert
is a semi-Hilbert 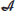 -module.
-module. -
(c)
Let
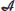 be a
be a 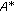 -algebra and
-algebra and  be the auxiliary norm on
be the auxiliary norm on  . If
. If 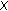 is an inner product
is an inner product  -module and
-module and 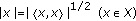 , then
, then 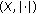 is a pre-Hilbert
is a pre-Hilbert 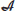 -module.
-module. -
(d)
Let
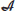 be a
be a 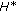 -algebra and
-algebra and  (a semi-inner product) an inner product
(a semi-inner product) an inner product 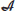 -module. Since tr is a positive linear functional on
-module. Since tr is a positive linear functional on  and for every
and for every  we have
we have 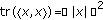 ; therefore
; therefore 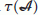 is a (semi-Hilbert) pre-Hilbert
is a (semi-Hilbert) pre-Hilbert  -module.
-module.
In the present paper, we give an analogue of the Bessel inequality (2.7) and we obtain some further generalization and a simple form for the Grüss type inequalities in inner product modules over  -algebras, proper
-algebras, proper  -algebras, and unital Banach
-algebras, and unital Banach  -algebras.
-algebras.
2. Schwarz and Bessel Inequality
If  is a semi-inner product
is a semi-inner product  -module, then the following Schwarz inequality holds:
-module, then the following Schwarz inequality holds:

(e.g. [4, Lemma 15.1.3]).
If  is a semi-inner product
is a semi-inner product  -module, then there are two forms of the Schwarz inequality: for every
-module, then there are two forms of the Schwarz inequality: for every 


First Saworotnow in [5] proved the strong Schwarz inequality, but the direct proof of that for a semi-inner product  -module can be found in [6].
-module can be found in [6].
Now let  be a
be a  -algebra,
-algebra,  a positive linear functional on
a positive linear functional on  and let
and let  be a semi-inner
be a semi-inner  -module. We can define a sesquilinear form on
-module. We can define a sesquilinear form on  by
by  ; the Schwarz inequality for
; the Schwarz inequality for  implies that
implies that

In [7, Proposition 1, Remark 1] the authors present two other forms of the Schwarz inequality in semi-inner  -module
-module  , one for positive linear functional
, one for positive linear functional  on
on  :
:

and another one for  -seminorm
-seminorm  on
on  :
:

The classical Bessel inequality states that if  is a family of orthonormal vectors in a Hilbert space
is a family of orthonormal vectors in a Hilbert space  , then
, then

Furthermore, some results concerning upper bounds for the expression

and for the expression related to the Grüss-type inequality

have been proved in [8]. A version of the Bessel inequality for inner product  -modules and inner product
-modules and inner product  -modules can be found in [9], also there is a version of it for Hilbert
-modules can be found in [9], also there is a version of it for Hilbert  -modules in [10, Theorem 3.1]. We provide here an analogue of the Bessel inequality for inner product
-modules in [10, Theorem 3.1]. We provide here an analogue of the Bessel inequality for inner product  -modules.
-modules.
Lemma 2.1.
Let  be a
be a  -algebra, let
-algebra, let  be an inner product
be an inner product  -module, and let
-module, and let  be a finite set of orthogonal elements in
be a finite set of orthogonal elements in  such that
such that  are idempotent. Then
are idempotent. Then

Proof.
By [11, Lemma 1] or a straightforward calculation shows that

3. Grüss Type Inequalities
Before stating the main results, let us fix the rest of our notation. We assume, unless stated otherwise, throughout this section that  is a unital Banach
is a unital Banach  -algebra. Also if
-algebra. Also if  is a semi-inner product
is a semi-inner product  -module and
-module and  is a
is a  -seminorm on
-seminorm on  , we put
, we put  , and if
, and if  is a positive linear functional on
is a positive linear functional on  , we put
, we put  . Let
. Let  be a finite set of orthogonal elements in
be a finite set of orthogonal elements in  such that
such that  be idempotent, we set
be idempotent, we set  and
and  .
.
Dragomir in [8, Lemma 4] shows that in a Hilbert space  , the condition
, the condition

is equivalent to the condition

where  and
and  ,
,  . But for semi-inner product
. But for semi-inner product  -modules we have the following lemma, which is a generalization of [7, Lemma 1].
-modules we have the following lemma, which is a generalization of [7, Lemma 1].
Lemma 3.1.
Let  be a semi-inner product
be a semi-inner product  -module and
-module and  ,
, 
 . Then
. Then

if and only if

Proof.
Follows from the equalities:

Remark 3.2.
By making use of the previous Lemma 3.1, we may conclude the following statements.
(i)Let  be an inner product
be an inner product  -module and let
-module and let  be a finite set of orthogonal elements in
be a finite set of orthogonal elements in  such that
such that  are idempotent, then inequality (3.3) implies that
are idempotent, then inequality (3.3) implies that

(ii)Let  be an inner product
be an inner product  -module and
-module and  be a finite set of orthogonal elements in
be a finite set of orthogonal elements in  such that
such that  are idempotent. If
are idempotent. If  is a
is a  -seminorm on
-seminorm on  then inequality (3.3) implies that
then inequality (3.3) implies that

and if  is a positive linear functional on
is a positive linear functional on  from inequality (3.3) and [2, Section 37 Lemma 6(iii)], we get
from inequality (3.3) and [2, Section 37 Lemma 6(iii)], we get

(iii)Let  be a proper
be a proper  -algebra, let
-algebra, let  be an inner product
be an inner product  -module, and let
-module, and let  be a finite set of orthogonal elements in
be a finite set of orthogonal elements in  such that
such that  are idempotent. Since for every
are idempotent. Since for every  ,
,  inequality (3.3) is valid only if
inequality (3.3) is valid only if

We are able now to state our first main result.
Theorem 3.3.
Let  be an inner product
be an inner product  -module and let
-module and let  be a finite set of orthogonal elements in
be a finite set of orthogonal elements in  such that
such that  are idempotent. If
are idempotent. If  ,
,  ,
,  ,
,  are real numbers and
are real numbers and  such that
such that

hold, then one has the inequality

Proof.
By [11, Lemma 2] or, a straightforward calculation shows that for every 

Therefore

Analogously, for every  , we have
, we have

The equalities (3.10), (3.13), and (3.14) imply that


Since

therefore the Schwarz's inequality (2.1) holds, that is,

Finally, using the elementary inequality for real numbers

on

we get

Remark 3.4.
-
(i)
Let
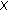 be an inner product
be an inner product  -module and let
-module and let  be a finite set of orthogonal elements in
be a finite set of orthogonal elements in 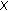 such that
such that 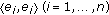 are idempotent. If
are idempotent. If  and
and 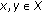 are such that
are such that 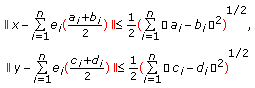 (3.22)
(3.22)
and if we put  , and
, and  , then, by (3.15) and (3.16), we have
, then, by (3.15) and (3.16), we have

These and (3.11) imply that

Therefore, (3.11) is a refinement and a simple formulation of [9, Theorem 4.1.].
-
(ii)
If for
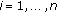 , we set
, we set 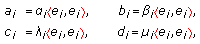 (3.25)
(3.25)
then similarly (3.11) is a refinement and a simple form of [9, Corollary 4.3].
Corollary 3.5.
Let  be a Banach
be a Banach  -algebra, let
-algebra, let  be an inner product
be an inner product  -module, and let
-module, and let  be a finite set of orthogonal elements in
be a finite set of orthogonal elements in  such that
such that  are idempotent. If
are idempotent. If  ,
,  ,
,  are real numbers and
are real numbers and  such that
such that

hold, then one has the inequality

Proof.
Using the schwarz's inequality (2.6), we have

The assumptions (3.26) and the elementary inequality for real numbers (3.19) will provide the desired result (3.27).
Example 3.6.
Let  be a Hermitian Banach
be a Hermitian Banach  -algebra and let
-algebra and let  be the Pták function on
be the Pták function on  . If
. If  is a semi-inner product
is a semi-inner product  -module and
-module and  with the properties that
with the properties that

then we have

That is interesting in its own right.
Corollary 3.7.
Let  be a proper
be a proper  -algebra, let
-algebra, let  be an inner product
be an inner product  -module, and let
-module, and let  be a finite set of orthogonal elements in
be a finite set of orthogonal elements in  such that
such that  are idempotent. If
are idempotent. If  ,
,  are real numbers and
are real numbers and  such that
such that

hold, then one has the inequality

Proof.
Using the strong Schwarz's inequality (2.3), we have

The assumptions (3.31) and the elementary inequality for real numbers (3.19) will provide (3.32).
The following companion of the Grüss inequality for positive linear functionals holds.
Theorem 3.8.
Let  be an inner product
be an inner product  -module, let
-module, let  be a positive linear functional on
be a positive linear functional on  , and let
, and let  be a finite set of orthogonal elements in
be a finite set of orthogonal elements in  such that
such that  are idempotent. If
are idempotent. If  ,
,  ,
,  ,
,  are real numbers and
are real numbers and  such that
such that

hold, then one has the inequality

Proof.
By taking  on both sides of (3.12), we have
on both sides of (3.12), we have

Analogously

Now, using Acz l's inequality for real numbers, that is, we recall that
l's inequality for real numbers, that is, we recall that

and the Schwarz's inequality for positive linear functionals, that is,

we deduce (3.35).
4. Some Related Results
Theorem 4.1.
Let  be an inner product
be an inner product  -module and let
-module and let  be a finite set of orthogonal elements in
be a finite set of orthogonal elements in  such that
such that  are idempotent. Let
are idempotent. Let  and if we define
and if we define

then we have

Proof.
For every  ,
,  , by (3.13) and (3.14), we have
, by (3.13) and (3.14), we have

Therefore

Now, using the elementary inequality for real numbers

on

we get

Corollary 4.2.
Let  be a Banach
be a Banach  -algebra, let
-algebra, let  be an inner product
be an inner product  -module, and let
-module, and let  be a finite set of orthogonal elements in
be a finite set of orthogonal elements in  such that
such that  are idempotent. Let
are idempotent. Let  and put
and put

then

Corollary 4.3.
Let  be a proper
be a proper  -algebra, let
-algebra, let  be an inner product
be an inner product  -module, and let
-module, and let  be a finite set of orthogonal elements in
be a finite set of orthogonal elements in  such that
such that  are idempotent. Let
are idempotent. Let  and if we consider
and if we consider

then

From a different perspective, we can state the following result as well.
Theorem 4.4.
Let  be an inner product
be an inner product  -module and let
-module and let  be a finite set of orthogonal elements in
be a finite set of orthogonal elements in  such that
such that  are idempotent. If
are idempotent. If  ,
,  ,
,  and
and  such that
such that

then we have the inequality

Proof.
We know that for any  and
and  one has
one has

Put  ,
,  , and since
, and since

using (4.14), we have

Now, inequality (4.13) follows from inequalities (3.15) and (4.16).
The following companion of the Grüss inequality for positive linear functionals holds.
Theorem 4.5.
Let  be an inner product
be an inner product  -module, let
-module, let  be a positive linear functional on
be a positive linear functional on  , and let
, and let  be a finite set of orthogonal elements in
be a finite set of orthogonal elements in  such that
such that  are idempotent. If
are idempotent. If  ,
,  ,
,  and
and  are such that
are such that

then we have the inequality

Proof.
The inequality (4.14) for  ,
,  implies that
implies that

By making use of inequality (3.12) for  instead of
instead of  and taking
and taking  on both sides, we have
on both sides, we have

From (4.19) and (4.20), we easily deduce (4.18).
Remark 4.6.
-
(i)
The constant 1 coefficient of
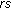 in (3.11) is sharp, in the sense that it cannot be replaced by a smaller quantity. If the submodule of
in (3.11) is sharp, in the sense that it cannot be replaced by a smaller quantity. If the submodule of 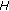 generated by
generated by  is not equal to
is not equal to 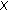 , then there exists
, then there exists 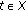 such that
such that 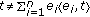 . We put
. We put 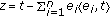 , then
, then 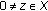 and for any
and for any 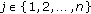 , we have
, we have 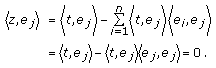 (4.21)
(4.21)
For every  , if we put
, if we put

then

therefore

Now if  is a constant such that
is a constant such that  , then there is a
, then there is a  such that
such that  ; therefore
; therefore

-
(ii)
Similarly, the constant 1 coefficient of
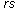 in (3.32) is best possible, it is sufficient instead of (4.22) to put
in (3.32) is best possible, it is sufficient instead of (4.22) to put 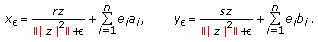 (4.26)
(4.26)
-
(iii)
If there is a nonzero element
 in
in 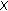 such that
such that  and
and 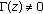 (resp.
(resp.  ) then the constant 1 coefficient of
) then the constant 1 coefficient of 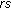 in (3.27) (resp. (3.35)) is best possible. Also similarly, the inequalities in Theorem 4.1, Corollaries 4.2 and 4.3, and Theorems 4.4 and 4.5 are sharp. However, the details are omitted.
in (3.27) (resp. (3.35)) is best possible. Also similarly, the inequalities in Theorem 4.1, Corollaries 4.2 and 4.3, and Theorems 4.4 and 4.5 are sharp. However, the details are omitted.
References
Doran RS, Belfi VA: Characterizations of C∗-Algebras, Monographs and Textbooks in Pure and Applied Mathematics. Volume 101. Marcel Dekker, New York, NY, USA; 1986:xi+426.
Bonsall FF, Duncan J: Complete Normed Algebras, Ergebnisse der Mathematik und ihrer Grenzgebiete. Volume 8. Springer, New York, NY, USA; 1973:x+301.
Pták V: On the spectral radius in Banach algebras with involution. The Bulletin of the London Mathematical Society 1970, 2: 327–334. 10.1112/blms/2.3.327
Wegge-Olsen NE: K-Theory and C∗-Algebras: A Friendly Approach, Oxford Science Publications. The Clarendon Press, Oxford University Press, New York, NY, USA; 1993:xii+370.
Saworotnow PP: A generalized Hilbert space. Duke Mathematical Journal 1968, 35: 191–197. 10.1215/S0012-7094-68-03520-5
Molnár L: A note on the strong Schwarz inequality in Hilbert
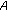 -modules. Publicationes Mathematicae Debrecen 1992,40(3–4):323–325.
-modules. Publicationes Mathematicae Debrecen 1992,40(3–4):323–325.Ghazanfari AG, Dragomir SS: Schwarz and Grüss type inequalities for
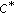 -seminorms and positive linear functionals on Banach
-seminorms and positive linear functionals on Banach  -modules. Linear Algebra and Its Applications 2011,434(4):944–956. 10.1016/j.laa.2010.10.010
-modules. Linear Algebra and Its Applications 2011,434(4):944–956. 10.1016/j.laa.2010.10.010Dragomir SS: Advances in Inequalities of the Schwarz, Grüss and Bessel Type in Inner Product Spaces. Nova Science, Hauppauge, NY, USA; 2005:viii+249.
Banić S, Ilišević D, Varošanec S: Bessel-and Grüss-type inequalities in inner product modules. Proceedings of the Edinburgh Mathematical Society 2007, 50: 23–36. 10.1017/S0013091505001021
Dragomir SS, Khosravi M, Moslehian MS: Bessel-type inequalities in hilbert
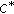 -modules. Linear and Multilinear Algebra 2010,58(8):967–975. 10.1080/03081080903113361
-modules. Linear and Multilinear Algebra 2010,58(8):967–975. 10.1080/03081080903113361Bakić D, Guljaš B: Hilbert
 -modules over
-modules over 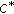 -algebras of compact operators. Acta Scientiarum Mathematicarum 2002,68(1–2):249–269.
-algebras of compact operators. Acta Scientiarum Mathematicarum 2002,68(1–2):249–269.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ghazanfari, A.G., Dragomir, S.S. Bessel and Grüss Type Inequalities in Inner Product Modules over Banach  -Algebras.
J Inequal Appl 2011, 562923 (2011). https://doi.org/10.1155/2011/562923
-Algebras.
J Inequal Appl 2011, 562923 (2011). https://doi.org/10.1155/2011/562923
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/562923
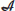 be a
be a  -algebra and
-algebra and  a positive linear functional or a
a positive linear functional or a  -seminorm on
-seminorm on  . It is known that
. It is known that 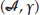 is a semi-Hilbert
is a semi-Hilbert 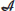 -module over itself with the inner product defined by
-module over itself with the inner product defined by 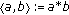 , in this case
, in this case  .
. be a Hermitian Banach
be a Hermitian Banach  -algebra and
-algebra and  be the Pták function on
be the Pták function on 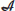 . If
. If 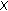 is a semi-inner product
is a semi-inner product 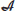 -module and
-module and 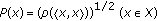 , then
, then  is a semi-Hilbert
is a semi-Hilbert  -module.
-module. be a
be a  -algebra and
-algebra and  be the auxiliary norm on
be the auxiliary norm on  . If
. If 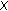 is an inner product
is an inner product  -module and
-module and 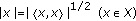 , then
, then 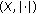 is a pre-Hilbert
is a pre-Hilbert 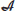 -module.
-module.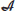 be a
be a 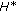 -algebra and
-algebra and  (a semi-inner product) an inner product
(a semi-inner product) an inner product 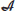 -module. Since tr is a positive linear functional on
-module. Since tr is a positive linear functional on  and for every
and for every  we have
we have 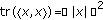 ; therefore
; therefore 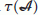 is a (semi-Hilbert) pre-Hilbert
is a (semi-Hilbert) pre-Hilbert  -module.
-module.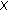 be an inner product
be an inner product  -module and let
-module and let  be a finite set of orthogonal elements in
be a finite set of orthogonal elements in 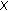 such that
such that 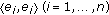 are idempotent. If
are idempotent. If  and
and 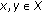 are such that
are such that 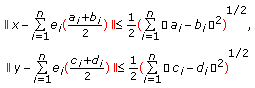
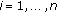 , we set
, we set 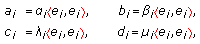
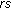 in (3.11) is sharp, in the sense that it cannot be replaced by a smaller quantity. If the submodule of
in (3.11) is sharp, in the sense that it cannot be replaced by a smaller quantity. If the submodule of 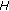 generated by
generated by  is not equal to
is not equal to 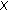 , then there exists
, then there exists 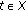 such that
such that 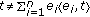 . We put
. We put 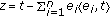 , then
, then 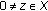 and for any
and for any 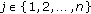 , we have
, we have 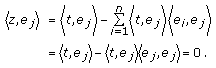
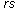 in (3.32) is best possible, it is sufficient instead of (4.22) to put
in (3.32) is best possible, it is sufficient instead of (4.22) to put 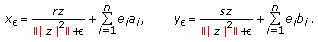
 in
in 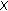 such that
such that  and
and 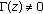 (resp.
(resp.  ) then the constant 1 coefficient of
) then the constant 1 coefficient of 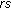 in (3.27) (resp. (3.35)) is best possible. Also similarly, the inequalities in Theorem 4.1, Corollaries 4.2 and 4.3, and Theorems 4.4 and 4.5 are sharp. However, the details are omitted.
in (3.27) (resp. (3.35)) is best possible. Also similarly, the inequalities in Theorem 4.1, Corollaries 4.2 and 4.3, and Theorems 4.4 and 4.5 are sharp. However, the details are omitted. -modules. Publicationes Mathematicae Debrecen 1992,40(3–4):323–325.
-modules. Publicationes Mathematicae Debrecen 1992,40(3–4):323–325. -seminorms and positive linear functionals on Banach
-seminorms and positive linear functionals on Banach  -modules. Linear Algebra and Its Applications 2011,434(4):944–956. 10.1016/j.laa.2010.10.010
-modules. Linear Algebra and Its Applications 2011,434(4):944–956. 10.1016/j.laa.2010.10.010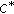 -modules. Linear and Multilinear Algebra 2010,58(8):967–975. 10.1080/03081080903113361
-modules. Linear and Multilinear Algebra 2010,58(8):967–975. 10.1080/03081080903113361 -modules over
-modules over 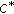 -algebras of compact operators. Acta Scientiarum Mathematicarum 2002,68(1–2):249–269.
-algebras of compact operators. Acta Scientiarum Mathematicarum 2002,68(1–2):249–269.