- Research Article
- Open access
- Published:
Riesz Potential on the Heisenberg Group
Journal of Inequalities and Applications volume 2011, Article number: 498638 (2011)
Abstract
The relation between Riesz potential and heat kernel on the Heisenberg group is studied. Moreover, the Hardy-Littlewood-Sobolev inequality is established.
1. Introduction
The classical Riesz potential  is defined on
is defined on  by
by

where  is the Laplacian operator. By virtue of the equations
is the Laplacian operator. By virtue of the equations

where  , one can get the explicit expression of Riesz potential
, one can get the explicit expression of Riesz potential

In addition, one has the following Hardy-Littlewood-Sobolev theorem (see [1]).
Theorem 1.1.
Let  ,
,  ,
,  . One has the following.
. One has the following.
(a)If  , then
, then  ;
;
(b)if  , then for all
, then for all  ,
,

In recent years many interesting works about the Riesz potential have been done by many authors. Thangavelu and Xu [2] discussed the Riesz potential for the Dunkl transform. Garofalo and Tyson [3] proved superposition principle Riesz potentials of nonnegative continuous function on Lie groups of Heisenberg type. Huang and Liu [4] studied the Hardy-Littlewood-Sobolev inequality of this operator on the Laguerre hypergroup. For more results about the Riesz potential, we refer the readers to see [5–9].
It is a remarkable fact that the Heisenberg group, denoted by  , arises in two aspects. On the one hand, it can be realized as the boundary of the unit ball in several complex variables. On the other hand, an important aspect of the study of the Heisenberg group is the background of physics, namely, the mathematical ideas connected with the fundamental notions of quantum mechanics. In other words, there is its genesis in the context of quantum mechanics which emphasizes its symplectic role in the theory of theta functions and related parts of analysis. Due to this reason, many interesting works were devoted to the theory of harmonic analysis on
, arises in two aspects. On the one hand, it can be realized as the boundary of the unit ball in several complex variables. On the other hand, an important aspect of the study of the Heisenberg group is the background of physics, namely, the mathematical ideas connected with the fundamental notions of quantum mechanics. In other words, there is its genesis in the context of quantum mechanics which emphasizes its symplectic role in the theory of theta functions and related parts of analysis. Due to this reason, many interesting works were devoted to the theory of harmonic analysis on  in [10–15] and the references therein.
in [10–15] and the references therein.
In present paper, we consider the Riesz potential associated with the Heisenberg group. We will show a connection between the Riesz potential and the heat kernel, and then get the Hardy-Littlewood-Sobolev inequality.
2. Preliminaries
The Heisenberg group  is a Lie group with the underlying manifold
is a Lie group with the underlying manifold  , the multiplication law is
, the multiplication law is

where  . The dilation of
. The dilation of  is defined by
is defined by  with
with  . For
. For  , the homogeneous norm of
, the homogeneous norm of  is given by
is given by

Note that  . In addition,
. In addition,  satisfies the quasi-triangle inequality
satisfies the quasi-triangle inequality

The ball of radius  centered at
centered at  is given by
is given by

For  , let
, let  be the space of measurable functions
be the space of measurable functions  on
on  , such that
, such that

Let  be the Schrödinger representations which acts on
be the Schrödinger representations which acts on  by
by

where  . Suppose that
. Suppose that  is a Schwartz function on
is a Schwartz function on  , that is,
, that is,  . The Fourier transform of
. The Fourier transform of  is defined by
is defined by

This means that, for each  ,
,

where  denotes the inner product.
denotes the inner product.
Let us write  with
with  and define
and define

Then (2.7) can be written as

If we set

then  . Let
. Let  ; one has the inversion of Fourier transform
; one has the inversion of Fourier transform

where  denotes the adjoint of
denotes the adjoint of  .
.
The convolution of  and
and  is defined by
is defined by

It is clear that  . In addition, we have the generalized Yong inequality
. In addition, we have the generalized Yong inequality

where  . More details about the harmonic analysis on Heisenberg group can be found in [14–16].
. More details about the harmonic analysis on Heisenberg group can be found in [14–16].
Let  be a mapping from
be a mapping from  to
to  ,
,  ,
,  . Then
. Then  is of type
is of type  if
if

where  does not depend on
does not depend on  . Similarly,
. Similarly,  is of weak type
is of weak type  if
if

where  does not depend on
does not depend on  or
or  (
( ).
).
Let  be the unit sphere in
be the unit sphere in  and
and  the unit Euclidean sphere in
the unit Euclidean sphere in  . Suppose that
. Suppose that  is a measurable function on
is a measurable function on  , and we have (see [10])
, and we have (see [10])

We set  , then
, then

Hence

A direct calculation shows that the area of  is
is

In addition, we have the volume of unit ball in 

and thus the volume of 

For a radial function  , we have
, we have

The Hardy-Littlewood maximal operator  is defined on
is defined on  by
by

which is of type  for
for  and is of weak type (1,1) (see [17, 18]).
and is of weak type (1,1) (see [17, 18]).
3. The Sublaplacian and the Heat Kernel on the Heisenberg Group
As it is known, the following vector fields

form a basis for the Lie algebra of left-invariant vector fields on  . The sublaplacian is defined by
. The sublaplacian is defined by

which also has another explicit form

where  is the standard Laplacian on
is the standard Laplacian on  and
and

For the Schrödinger representations  one easily calculates that
one easily calculates that

So that  .
.
Let  (
( ) be the normalized Hermite functions given by
) be the normalized Hermite functions given by

where  . For
. For  and
and  , we define
, we define

Then  forms an orthonormal basis for
forms an orthonormal basis for  .
.
We set  and denote
and denote

Therefore,

Moreover, one has

Now let  , then
, then  has the form
has the form

From (3.9) we know that the functions

are eigenfunctions of the operator  :
:

Let  be the Laguerre functions defined on
be the Laguerre functions defined on  by
by

and set  for
for  . Then from [19, (2.3.26)] we have
. Then from [19, (2.3.26)] we have

In view of this equation we have the following.
Proposition 3.1.
One has

where  stands for the projection of
stands for the projection of  onto the
onto the  th eigenspace of
th eigenspace of  , that is,
, that is,

Now we consider the heat equation associated to the sublaplacian

with the initial condition  . In fact, the function
. In fact, the function  given by
given by

is just the solution of the heat equation and satisfies

Moreover, we have the Fourier transform of  (see [18, page 86])
(see [18, page 86])

4. Riesz Potential on the Heisenberg Group
In Section 1 we have recalled some properties about the Riesz potential on  ; now we are going to discuss the Riesz potential on the Heisenberg group.
; now we are going to discuss the Riesz potential on the Heisenberg group.
Definition 4.1.
For  , the Riesz potential
, the Riesz potential  is defined on
is defined on  by
by

From above definition and (3.10) it is easy to see that

If  ,
,  , then we have
, then we have

which suggests that  . Especially, for
. Especially, for  , one has
, one has

At present we do not prepare to gain the expression of  analogues to (1.3) because it is hard to calculate the Fourier transform of
analogues to (1.3) because it is hard to calculate the Fourier transform of  . But the following theorem will give us another expression of
. But the following theorem will give us another expression of  , which provides a bridge to discuss the boundedness of the Riesz potential.
, which provides a bridge to discuss the boundedness of the Riesz potential.
Theorem 4.2.
Let  be the heat kernel on
be the heat kernel on  . For
. For  , one has for
, one has for 

Proof.
By (3.17), (3.21), and Proposition 3.1 we have

Then we get the desired result.
Lemma 4.3.
The heat kernel  satisfies the estimate
satisfies the estimate

with some positive constants  and
and  .
.
Proof.
Since  , then by [19, Proposition 2.8.2] we obtain this lemma.
, then by [19, Proposition 2.8.2] we obtain this lemma.
The following theorem is an immediate consequence of Theorem 4.2 and Lemma 4.3.
Theorem 4.4.
The Riesz potential  satisfies the estimate
satisfies the estimate

where  is a positive constant.
is a positive constant.
Using Theorems 4.2 and 4.4, we get the Hardy-Littlewood-Sobolev theorem on the Heisenberg group.
Theorem 4.5.
Let  ,
,  , and
, and  . For
. For  , one has the following.
, one has the following.
(a)If  , then
, then  is of type
is of type  .
.
(b)If  , then
, then  is of weak type
is of weak type  .
.
Proof.
Let  be the maximal operator defined by (2.24). We claim that
be the maximal operator defined by (2.24). We claim that

Let  be the ball of radius
be the ball of radius  centered at (0,0), and let
centered at (0,0), and let  be its characteristic function. We set
be its characteristic function. We set

with  . Obviously,
. Obviously,  is radial and decreasing, then we can write
is radial and decreasing, then we can write

where  and
and  is the ball centered at origin. By (2.23) and (2.24) we have
is the ball centered at origin. By (2.23) and (2.24) we have

Let  be the conjugate exponent of
be the conjugate exponent of  . Since
. Since  , we have
, we have

Then by Hölder's inequality we get

Therefore,

We choose  such that
such that

That is,  . Substituting this in the above then gives (4.9).
. Substituting this in the above then gives (4.9).
Now if  , we obtain (a) by the virtue of the type
, we obtain (a) by the virtue of the type  of the maximal operator
of the maximal operator  . If
. If  and
and  , we have
, we have

This proves our main theorem.
Theorem 4.6.
Let  and
and  . For
. For  , one has the following.
, one has the following.
(a)If  , then the condition
, then the condition  is necessary and sufficient for the weak type
is necessary and sufficient for the weak type  of
of  .
.
-
(b)
If
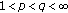 , then the condition
, then the condition  is necessary and sufficient for the type
is necessary and sufficient for the type 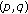 of
of 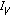 .
.
Proof.
The sufficiency follows from Theorem 4.5. We now begin to prove the necessity. Suppose that  , and let
, and let  . Note that
. Note that

Then by (4.9) we get

Thus for  , we have
, we have

Case 1 ( ).
).
It follows from the hypothesis that

If  , then
, then  as
as  . If
. If  , then
, then  as
as  . Thus we have
. Thus we have  .
.
Case 2 ( ).
).
Similarly, we have

which implies that  .
.
Then we complete the proof of this theorem.
References
Stein EM: Singular Integrals and Differentiability Properties of Functions, Princeton Mathematical Series, no. 30. Princeton University Press, Princeton, NJ, USA; 1970:xiv+290.
Thangavelu S, Xu Y: Riesz transform and Riesz potentials for Dunkl transform. Journal of Computational and Applied Mathematics 2007,199(1):181–195. 10.1016/j.cam.2005.02.022
Garofalo N, Tyson JT: Riesz potentials and -superharmonic functions in Lie groups of Heisenberg type. http://arxiv.org/abs/arXiv:1005.4090
Huang J, Liu H: Riesz potential on the Laguerre hypergroup. http://www.paper.edu.cn/index.php/default/releasepaper/paper_all/9592
Chen Y, Ding Y, Wang X: Compactness of commutators of Riesz potential on Morrey spaces. Potential Analysis 2009,30(4):301–313. 10.1007/s11118-008-9114-4
Cowling M, Meda S, Pasquale R: Riesz potentials and amalgams. Annales de l'Institut Fourier 1999,49(4):1345–1367. 10.5802/aif.1720
Rubin B: Inversion of potentials in
 by means of Gauss-Weierstrass integrals. Mathematical Notes 1987,41(1):22–27. 10.1007/BF01159524
by means of Gauss-Weierstrass integrals. Mathematical Notes 1987,41(1):22–27. 10.1007/BF01159524Sezer S, Aliev IA: A new characterization of the Riesz potential spaces with the aid of a composite wavelet transform. Journal of Mathematical Analysis and Applications 2010,372(2):549–558. 10.1016/j.jmaa.2010.07.009
Stein EM: The characterization of functions arising as potentials. Bulletin of the American Mathematical Society 1961,67(1):102–104. 10.1090/S0002-9904-1961-10517-X
Coulhon T, Müller D, Zienkiewicz J: About Riesz transforms on the Heisenberg groups. Mathematische Annalen 1996,305(1):369–379. 10.1007/BF01444227
Müller D, Ricci F, Stein EM: Marcinkiewicz multipliers and multi-parameter structure on Heisenberg (-type) groups. I. Inventiones Mathematicae 1995,119(1):199–233. 10.1007/BF01245180
Müller D, Ricci F, Stein EM: Marcinkiewicz multipliers and multi-parameter structure on Heisenberg (-type) groups. II. Mathematische Zeitschrift 1996,221(1):267–291. 10.1007/BF02622116
Rubin B: The Radon transform on the Heisenberg group and the transversal Radon transform. http://arxiv.org/abs/0910.2312
Stein EM: Harmonic Analysis: Real-Variable Methods, Orthogonality, and Oscillatory Integrals, Princeton Mathematical Series. Volume 43. Princeton University Press, Princeton, NJ, USA; 1993:xiv+695.
Thangavelu S: Harmonic Analysis on the Heisenberg Group, Progress in Mathematics. Volume 159. Birkhäuser, Boston, Mass, USA; 1998:xiv+192.
Folland GB: Harmonic Analysis in Phase Space, Annals of Mathematics Studies. Volume 122. Princeton University Press, Princeton, NJ, USA; 1989:x+277.
Folland GB, Stein EM: Hardy Spaces on Homogeneous Groups, Mathematical Notes. Volume 28. Princeton University Press, Princeton, NJ, USA; 1982:xii+285.
Müller D: Marcinkiewicz Multipliers and Multi-Parameter Structure on Heisenberg Groups, Lecture Notes. Università degli Studi di Padova; 2004.
Thangavelu S: An Introduction to the Uncertainty Principle: Hardy's Theorem on Lie Groups, Progress in Mathematics. Volume 217. Birkhäuser, Boston, Mass, USA; 2004:xiv+174.
Acknowledgments
The work for this paper is supported by the National Natural Science Foundation of China (no. 10971039) and the Doctoral Program Foundation of the Ministry of China (no. 200810780002). The authors are also grateful for the referee for the valuable suggestions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Xiao, J., He, J. Riesz Potential on the Heisenberg Group. J Inequal Appl 2011, 498638 (2011). https://doi.org/10.1155/2011/498638
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/498638
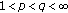 , then the condition
, then the condition  is necessary and sufficient for the type
is necessary and sufficient for the type 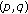 of
of 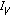 .
. by means of Gauss-Weierstrass integrals. Mathematical Notes 1987,41(1):22–27. 10.1007/BF01159524
by means of Gauss-Weierstrass integrals. Mathematical Notes 1987,41(1):22–27. 10.1007/BF01159524