- Research Article
- Open access
- Published:
Notes on  Summability Factors of Infinite Series
Summability Factors of Infinite Series
Journal of Inequalities and Applications volume 2011, Article number: 365453 (2011)
Abstract
New result concerning  summability of the infinite series
summability of the infinite series  is presented.
is presented.
1. Introduction
Let  be a given infinite series with sequence of partial sums
be a given infinite series with sequence of partial sums  . Let
. Let  denote the sequence of
denote the sequence of  means of
means of  . The
. The  transform of
transform of  is defined by
is defined by

where

Necessary and sufficient conditions for the  method to be regular are
method to be regular are
(i) for each
for each  ,
,
(ii) , where
, where  is a positive constant independent of
is a positive constant independent of  .
.
The series  is said to be summable
is said to be summable  ,
,  , if
, if

where

where  as
as  .
.
The series  is said to be summable
is said to be summable  , if
, if

where

and it is said to be summable  ,
,  , if
, if

where  is as defined by (1.1).
is as defined by (1.1).
For  ,
,  summability reduces to
summability reduces to  summability.
summability.
The series  is said to be
is said to be  bounded or
bounded or  if
if

By  , we denote the set of sequences
, we denote the set of sequences  satisfying
satisfying

It is known (Das [1]) that for  , (1.5) holds if and only if
, (1.5) holds if and only if

For  , the series
, the series  is said to be
is said to be  -summable,
-summable,  , (Sulaiman [2]), if
, (Sulaiman [2]), if

where  as
as  .
.
It is quite reasonable to give the following definition.
For  , the series
, the series  is said to be
is said to be  -summable,
-summable,  , if
, if

where  as
as  .
.
We also assume that  ,
,  are positive sequences of numbers such that
are positive sequences of numbers such that

A positive sequence  is said to be a quasi-
is said to be a quasi- -power increasing sequence,
-power increasing sequence,  , if there exists a constant
, if there exists a constant  such that
such that

holds for  (see [3]).
(see [3]).
Das [1], in 1966, proved the following result.
Theorem 1.1.
Let  ,
,  . Then if
. Then if  is
is  -summable, it is
-summable, it is  -summable.
-summable.
Recently Singh and Sharma [4] proved the following theorem.
Theorem 1.2.
Let  ,
,  and let
and let  be a monotonic nondecreasing sequence for
be a monotonic nondecreasing sequence for  . The necessary and sufficient condition that
. The necessary and sufficient condition that  is
is  -summable whenever
-summable whenever

is that

2. Lemmas
Lemma 2.1.
Let  be nonincreasing,
be nonincreasing,  . Then for
. Then for  ,
,  ,
,

Proof.
Since  is nonincreasing, then
is nonincreasing, then  .
.

Therefore

Lemma 2.2.
For  ,
,

Proof.
Since  , then
, then  is nonincreasing and hence
is nonincreasing and hence

Lemma 2.3 (see [3]).
If  is a quasi-f-increasing sequence, where
is a quasi-f-increasing sequence, where  ,
,  ,
,  , then under the conditions
, then under the conditions

one has

3. Result
Our aim is to present the following new general result.
Theorem 3.1.
Let  , and let
, and let  be a quasi-f-increasing sequence, where
be a quasi-f-increasing sequence, where  ,
,  ,
,  and (2.6), and
and (2.6), and

are all satisfied, then the series  is summable
is summable  ,
,  .
.
Proof.
We have

In order to prove the result, it is sufficient, by Minkowski's inequality, to show that

Applying HÖlder's inequality, we have

This completes the proof of the theorem.
References
Das G: On some methods of summability. The Quarterly Journal of Mathematics Oxford Series 1966,17(2):244–256.
Sulaiman WT: Notes on two summability methods. Pure and Applied Mathematika Sciences 1990,31(1–2):59–69.
Sulaiman WT: Extension on absolute summability factors of infinite series. Journal of Mathematical Analysis and Applications 2006,322(2):1224–1230. 10.1016/j.jmaa.2005.09.019
Singh N, Sharma N: On
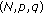 summability factors of infinite series. Proceedings of Mathematical Sciences 2000,110(1):61–68. 10.1007/BF02829481
summability factors of infinite series. Proceedings of Mathematical Sciences 2000,110(1):61–68. 10.1007/BF02829481
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Sulaiman, W.T. Notes on  Summability Factors of Infinite Series.
J Inequal Appl 2011, 365453 (2011). https://doi.org/10.1155/2011/365453
Summability Factors of Infinite Series.
J Inequal Appl 2011, 365453 (2011). https://doi.org/10.1155/2011/365453
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/365453
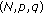 summability factors of infinite series. Proceedings of Mathematical Sciences 2000,110(1):61–68. 10.1007/BF02829481
summability factors of infinite series. Proceedings of Mathematical Sciences 2000,110(1):61–68. 10.1007/BF02829481