- Research Article
- Open access
- Published:
Refinements of Results about Weighted Mixed Symmetric Means and Related Cauchy Means
Journal of Inequalities and Applications volume 2011, Article number: 350973 (2011)
Abstract
A recent refinement of the classical discrete Jensen inequality is given by Horváth and Pečarić. In this paper, the corresponding weighted mixed symmetric means and Cauchy-type means are defined. We investigate the exponential convexity of some functions, study mean value theorems, and prove the monotonicity of the introduced means.
1. Introduction and Preliminary Results
A new refinement of the discrete Jensen inequality is given in [1]. The following notations are also introduced in [1].
Let  be a set,
be a set,  its power set, and
its power set, and  denotes the number of elements in
denotes the number of elements in  . Let
. Let  and
and  be fixed integers. Define the functions
be fixed integers. Define the functions

by

Further, introduce the function

via

For each  , let
, let

It is easy to observe from the construction of the functions  and
and  that they do not depend essentially on
that they do not depend essentially on  , so we can write for short
, so we can write for short  for
for  , and so on.
, and so on.
(H1) The following considerations concern a subset  of
of  satisfying
satisfying

where  and
and  are fixed integers.
are fixed integers.
Next, we proceed inductively to define the sets  by
by

By (1.6),  and this implies that
and this implies that  for
for  . From (1.6), again, we have
. From (1.6), again, we have  .
.
For every  and for any
and for any  , let
, let

Using these sets we define the functions  inductively by
inductively by

Let  be an interval in
be an interval in  , let
, let  , let
, let  such that
such that  and
and  , and let
, and let  be a convex function. For any
be a convex function. For any  , set
, set

and associate to each  the number
the number

We need the following hypotheses.
(H2)Let  and
and  be positive
be positive  -tuples such that
-tuples such that  .
.
(H3) Let  be an interval, let
be an interval, let  , let
, let  be a positive
be a positive  -tuples such that
-tuples such that  , and let
, and let  ,
,  be continuous and strictly monotone functions.
be continuous and strictly monotone functions.
(H4) Let  be an interval, let
be an interval, let  , and let
, and let  be positive
be positive  -tuples such that
-tuples such that  . Further, let
. Further, let  be a convex function.
be a convex function.
Assume (H1) and (H2). The power means of order  corresponding to
corresponding to  are given as
are given as

We also use the means

For  ,
,  , we introduce the mixed symmetric means with positive weights as follows:
, we introduce the mixed symmetric means with positive weights as follows:

and, for  ,
,

We deduce the monotonicity of these means from the following refinement of the discrete Jensen inequality in [1].
Theorem 1.1.
Assume (H1) and (H4). Then,

where the numbers  are defined in (1.10) and (1.11). If
are defined in (1.10) and (1.11). If  is a concave function, then the inequalities in (1.16) are reversed.
is a concave function, then the inequalities in (1.16) are reversed.
Under the conditions of the previous theorem,

Corollary 1.2.
Assume (H1) and (H2). Let  ,
,  such that
such that  , then
, then


Proof.
Assume  . To obtain (1.18), we can apply Theorem 1.1 to the function
. To obtain (1.18), we can apply Theorem 1.1 to the function  and the
and the  -tuples
-tuples  to get the analogue of (1.16) and to raise the power
to get the analogue of (1.16) and to raise the power  . Equation (1.19) can be proved in a similar way by using
. Equation (1.19) can be proved in a similar way by using  and
and  and raising the power
and raising the power  .
.
When  or
or  , we get the required results by taking limit.
, we get the required results by taking limit.
Assume (H1) and (H3). Then, we define the quasiarithmetic means with respect to (1.10) and (1.11) as follows:

and, for  ,
,

The monotonicity of these generalized means is obtained in the next corollary.
Corollary 1.3.
Assume (H1) and (H3). For a continuous and strictly monotone function  , one defines
, one defines

Then,

if either  is convex and
is convex and  is increasing or
is increasing or  is concave and
is concave and  is decreasing,
is decreasing,

if either  is convex and
is convex and  is decreasing or
is decreasing or  is concave and
is concave and  is increasing.
is increasing.
Proof.
First, we can apply Theorem 1.1 to the function  and the
and the  -tuples
-tuples  , then we can apply
, then we can apply  to the inequality coming from (1.16). This gives (1.23). A similar argument gives (1.24):
to the inequality coming from (1.16). This gives (1.23). A similar argument gives (1.24):  and
and  can be used.
can be used.
Throughout Examples 1.4-1.5, 1.9–1.12, which are based on examples in [1], the conditions (H2), in the mixed symmetric means, and (H3), in the quasiarithmetic means, will be assumed.
Example 1.4.
Suppose

where  means that
means that  divides
divides  . Since
. Since  , therefore (1.6) holds. We note that
, therefore (1.6) holds. We note that

where  is the largest positive integer not greater than
is the largest positive integer not greater than  , and
, and  means the number of positive divisors of
means the number of positive divisors of  . Then, (1.14) gives for
. Then, (1.14) gives for  ,
, 

while (1.20) gives

Assume (H4) holds, and consider the set  in Example 1.4. Then, Theorem 1.1 implies that
in Example 1.4. Then, Theorem 1.1 implies that

and thus

Example 1.5.
Let  be an integer
be an integer  , let
, let  , and also let
, and also let  consist of all sequences
consist of all sequences  in which the number of occurrences of
in which the number of occurrences of  is
is  . Obviously, (1.6) holds, and, by simple calculations, we have
. Obviously, (1.6) holds, and, by simple calculations, we have

Moreover,  for
for

Under the above settings, (1.15) can be written as

while (1.21) becomes

Assume (H4) holds, and consider the set  in Example 1.5. Then, Theorem 1.1 yields that
in Example 1.5. Then, Theorem 1.1 yields that

This shows that

The following result is also given in [1].
Theorem 1.6.
Assume (H1) and (H4), and suppose  for any
for any  . Then,
. Then,

and thus

If  is a concave function then the inequalities (1.38) are reversed.
is a concave function then the inequalities (1.38) are reversed.
Under the conditions of the previous theorem, we have, from (1.38), that

Assume (H1) and (H2), and suppose  for any
for any  . In this case, the power means of order
. In this case, the power means of order  corresponding to
corresponding to  has the form
has the form

Now, for  ,
,  and
and  , we introduce the mixed symmetric means with positive weights related to (1.37) as follows:
, we introduce the mixed symmetric means with positive weights related to (1.37) as follows:

Corollary 1.7.
Assume (H1) and (H2), and suppose  for any
for any 
 . Let
. Let  ,
,  such that
such that  . Then,
. Then,

Proof.
The proof comes from Corollary 1.2.
Assume (H1) and (H3), and suppose  for any
for any  . We define for
. We define for  the quasiarithmetic means with respect to (1.37) as follows:
the quasiarithmetic means with respect to (1.37) as follows:

Corollary 1.8.
Assume (H1) and (H3), and suppose  for any
for any  . Then,
. Then,

where either  is convex and
is convex and  is increasing or
is increasing or  is concave and
is concave and  is decreasing,
is decreasing,

where either  is convex and
is convex and  is decreasing or
is decreasing or  is concave and
is concave and  is increasing.
is increasing.
Proof.
The proof is a consequence of Corollary 1.3.
Example 1.9.
If we set

then  , that is, (1.6) is satisfied for
, that is, (1.6) is satisfied for  . It comes easily that
. It comes easily that  ,
,  , and for each
, and for each 

In this case, (1.41) becomes for 

and (1.43) has the form

Equation (1.48) is a weighted mixed symmetric mean and (1.49) is a generalized mean, as given in [2]. Therefore, Corollaries 1.7 and 1.8 are more general than the Corollaries 1.2 and 1.3 given in [2].
Assume (H4) holds, and consider the set  in Example 1.9. Then, Theorem 1.6 shows that
in Example 1.9. Then, Theorem 1.6 shows that

Thus, we have

Example 1.10.
If we set

then  and thus (1.6) is satisfied. It is easy to see that
and thus (1.6) is satisfied. It is easy to see that  ,
,  , and for each
, and for each 

Under these settings (1.41) becomes

and (1.43) has the form

Equation (1.54) represents weighted mixed symmetric means, and (1.55) defines generalized means, as given in [2]. Therefore, Corollaries 1.7 and 1.8 are more general than the Corollaries 1.9 and 1.10 given in [2].
Assume (H4) holds, and consider the set  in Example 1.10. Then, it follows from Theorem 1.6 that
in Example 1.10. Then, it follows from Theorem 1.6 that

where

This yields that

Example 1.11.
We set

Then,  , hence (1.6) holds. It is not hard to see that
, hence (1.6) holds. It is not hard to see that  , and for each
, and for each  ,
,

Therefore, under these settings, for  , (1.41) leads to
, (1.41) leads to

and (1.43) gives

respectively.
Assume (H4) holds, and consider the set  in Example 1.11. Then, Theorem 1.6 implies that
in Example 1.11. Then, Theorem 1.6 implies that

where

Therefore, we have

Example 1.12.
Let  and let
and let  consist of all sequences
consist of all sequences  of
of  distinct numbers from
distinct numbers from  . Then,
. Then,  , hence (1.6) holds. It is immediate that
, hence (1.6) holds. It is immediate that  , and for every
, and for every  ,
,

Therefore under these settings, for  , (1.41) gives
, (1.41) gives

and (1.43) has the form

respectively.
Assume (H4) holds, and consider the set  in Example 1.12. Then, Theorem 1.6 yields that
in Example 1.12. Then, Theorem 1.6 yields that

where for  ,
,

Therefore, we have

2. Main Results
We have seen that

From now on, (H1) and (H4) are assumed if we consider  , further, the hypothesis
, further, the hypothesis  for any
for any  is also assumed if we consider
is also assumed if we consider  . The numbers
. The numbers  are generated by concrete examples, and (H4) is assumed.
are generated by concrete examples, and (H4) is assumed.
We need the following subclass of convex functions (see [3]).
Definition 2.1.
A function  is exponentially convex if it is continuous and
is exponentially convex if it is continuous and

for all  and all choices
and all choices  and
and  .
.
We quote here useful propositions from [3].
Proposition 2.2.
Let  be a function. Then, the following statements are equivalent
be a function. Then, the following statements are equivalent
(i) is exponentially convex.
is exponentially convex.
(ii) is continuous and
is continuous and

for every  and every
and every  .
.
Proposition 2.3.
If  is an exponentially convex function, then
is an exponentially convex function, then  is log-convex which means that for every
is log-convex which means that for every  ,
,  and all
and all 

First, we introduce a special class of functions.
(H5) Let  be a set of twice differentiable convex functions such that the function
be a set of twice differentiable convex functions such that the function 
 is exponentially convex for every fixed
is exponentially convex for every fixed  .
.
As examples, consider two classes of functions  defined by
defined by

and  defined by
defined by

It is easy to see that the sets of functions  and
and  satisfy (H5).
satisfy (H5).
Assume (H5). If  is replaced by
is replaced by  in (2.1), we obtain
in (2.1), we obtain

Especially,

In this paper we prove the exponential convexity of the functions  , and we give mean value theorems for
, and we give mean value theorems for  . We also define the respective means of Cauchy type and study their monotonicity. The results for
. We also define the respective means of Cauchy type and study their monotonicity. The results for  are special cases of the results for
are special cases of the results for  , and the results for
, and the results for  are special cases of results for
are special cases of results for  . Especially, the results for
. Especially, the results for  are also given in [2].
are also given in [2].
Theorem 2.4.
Assume (H5), and suppose that the functions 
 are continuous. The following statements hold for
are continuous. The following statements hold for  .
.
(a)For every  and
and  , the matrix
, the matrix  is positive semidefinite. Particularly,
is positive semidefinite. Particularly,

(b)The function  is exponentially convex.
is exponentially convex.
Proof.
Fix  .
.
(a)Let  , and define the functions
, and define the functions  by
by  for
for  , where
, where  . Then
. Then  is a convex function since
is a convex function since

By taking  in (2.1), we have
in (2.1), we have

This means that the matrix  is positive semidefinite, that is, (2.9) is valid.
is positive semidefinite, that is, (2.9) is valid.
(b)It is assumed that the function  is continuous. By using Poposition 2.2 and (a), we get the exponential convexity of the function
is continuous. By using Poposition 2.2 and (a), we get the exponential convexity of the function  .
.
Since the functions  are continuous
are continuous  , we have the following.
, we have the following.
Corollary 2.5.
The function  are exponentially convex. This remains valid if we replace
are exponentially convex. This remains valid if we replace  by
by  in (2.8).
in (2.8).
3. Cauchy Means
In this section, first, we are interested in mean value theorems.
Theorem 3.1.
Assume  and
and  . Then, there exists
. Then, there exists  such that
such that

Theorem 3.2.
Assume  ,
,  . Then, there exists
. Then, there exists  such that
such that

provided that the denominators are nonzero.
The idea of the proofs of Theorems 3.1 and 3.2 is the same as the proofs of Theorems 2.3 and 2.4 in [2].
Corollary 3.3.
Let  ,
,  ,
,  and
and  . Then, for distinct real numbers
. Then, for distinct real numbers  and
and  , different from 0 and 1, there exists
, different from 0 and 1, there exists  such that
such that

Proof.
Theorem 3.2 can be applied.
Remark 3.4.
Suppose the conditions of Corollary 3.3 are satisfied.
(a)Since the function  ,
,  is invertible, then we get, from (3.3), that for
is invertible, then we get, from (3.3), that for 

-
(b)
By choosing
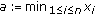 and
and 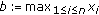 , we can see that the expression between
, we can see that the expression between  and
and  in (3.4) defines a mean.
in (3.4) defines a mean.
Corollary 3.5.
Assume (H1) and (H2), and suppose  . In (3.6), it is also supposed that
. In (3.6), it is also supposed that  for any
for any 
 . Then, for distinct real numbers
. Then, for distinct real numbers  ,
,  , and
, and  , all are different from 0 and 1, there exists
, all are different from 0 and 1, there exists  , such that
, such that


Proof.
We can apply Theorem 3.2 to the functions  ,
,  ,
,  , and
, and  , and the
, and the  -tuples
-tuples  .
.
Remark 3.6.
Suppose the conditions of Corollary 3.5 are satisfied.
(a)Since the function  is invertible, then we get, from (3.5) and (3.6) that
is invertible, then we get, from (3.5) and (3.6) that

(b)As in Remark 3.4 (b), the expressions in (3.7) define means.
By Remark 3.4 (b), we can define Cauchy means for  as follows:
as follows:

Moreover, we have continuous extensions of these means in other cases. By taking the limit, we have

Now, we deduce the monotonicity of these means in the form of Dresher's inequality as follows.
Theorem 3.7.
Let  such that
such that  . Then
. Then

Proof.
Fix  . Corollary 2.5 shows that the function
. Corollary 2.5 shows that the function  is exponentially convex, and hence, by Proposition 2.3, it is log-convex. Therefore, the function
is exponentially convex, and hence, by Proposition 2.3, it is log-convex. Therefore, the function  is convex, which implies (see [4]) that
is convex, which implies (see [4]) that

This gives (3.10) if  and
and  . The other cases come from this by taking limit.
. The other cases come from this by taking limit.
By Remark 3.6 (b), we can define Cauchy means in the following form:

where  . By taking the limit, we have
. By taking the limit, we have

where  .
.
Now, we give the monotonicity of these new means.
Theorem 3.8.
Let  such that
such that  . Then,
. Then,

Proof.
Suppose  , 2 is fixed. The function
, 2 is fixed. The function  is exponentially convex, and hence, by Proposition 2.3, it is log-convex. Therefore, the function
is exponentially convex, and hence, by Proposition 2.3, it is log-convex. Therefore, the function  is convex, which implies (as in the proof of Theorem 3.7) that
is convex, which implies (as in the proof of Theorem 3.7) that

If  , set
, set  in (3.15) to obtain (3.14).
in (3.15) to obtain (3.14).
For  , we get the required result by limit.
, we get the required result by limit.
Funding
This research was partially funded by the Higher Education Commission, Pakistan.
References
Horváth L, Pečarić J: A refinement of the discrete Jensen's inequality. to appear in Mathematical Inequalities and Applications
Khan KA, Pečarić J, Perić I: Differences of weighted mixed symmetric means and related results. journal of Inequalities and Applications 2010, 2010:-16.
Anwar M, Jakšetić J, Pečarić J, Ur Rehman A: Exponential convexity, positive semi-definite matrices and fundamental inequalities. Journal of Mathematical Inequalities 2010,4(2):171–189.
Pečarić JE, Proschan F, Tong YL: Convex Functions, Partial Orderings and Statistical Applications, Mathematics in Science and Engineering. Volume 187. Academic Press, Boston, Mass, USA; 1992:xiv+467.
Acknowledgments
The research of L. Horváth was supported by the Hungarian National Foundations for Scientific Research, Grant no. K73274, and that of J. Pecărić was supported by the Croatian Ministry of Science, Education, and Sports under the research Grant 117-1170889-0888.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Horváth, L., Khan, K. & Pečarić, J. Refinements of Results about Weighted Mixed Symmetric Means and Related Cauchy Means. J Inequal Appl 2011, 350973 (2011). https://doi.org/10.1155/2011/350973
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/350973
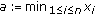 and
and 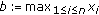 , we can see that the expression between
, we can see that the expression between  and
and  in (3.4) defines a mean.
in (3.4) defines a mean.