- Review Article
- Open access
- Published:
Nonlinear 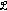 -Random Stability of an ACQ Functional Equation
-Random Stability of an ACQ Functional Equation
Journal of Inequalities and Applications volume 2011, Article number: 194394 (2011)
Abstract
We prove the generalized Hyers-Ulam stability of the following additive-cubic-quartic functional equation:  in complete latticetic random normed spaces.
in complete latticetic random normed spaces.
1. Introduction
Random theory is a powerful hand set for modeling uncertainty and vagueness in various problems arising in the field of science and engineering. It has also very useful applications in various fields, for example, population dynamics, chaos control, computer programming, nonlinear dynamical systems, nonlinear operators, statistical convergence, and so forth. The random topology proves to be a very useful tool to deal with such situations where the use of classical theories breaks down. The usual uncertainty principle of Werner Heisenberg leads to a generalized uncertainty principle, which has been motivated by string theory and noncommutative geometry. In strong quantum gravity regime space-time points are determined in a random manner. Thus impossibility of determining the position of particles gives the space-time a random structure. Because of this random structure, position space representation of quantum mechanics breaks down, and therefore a generalized normed space of quasiposition eigenfunction is required. Hence, one needs to discuss on a new family of random norms. There are many situations where the norm of a vector is not possible to be found and the concept of random norm seems to be more suitable in such cases, that is, we can deal with such situations by modeling the inexactness through the random norm [1, 2].
The stability problem of functional equations originated from a question of Ulam [3] concerning the stability of group homomorphisms. Hyers [4] gave a first affirmative partial answer to the question of Ulam for Banach spaces. Hyers' theorem was generalized by Aoki [5] for additive mappings and by Th. M. Rassias [6] for linear mappings by considering an unbounded Cauchy difference. The paper of Th. M. Rassias [6] has provided a lot of influence in the development of what we call generalized Hyers-Ulam stability or as Hyers-Ulam-Rassias stability of functional equations

A generalization of the Th. M. Rassias theorem was obtained by Găvruţa [7] by replacing the unbounded Cauchy difference by a general control function in the spirit of Th. M. Rassias approach.
The stability problems of several functional equations have been extensively investigated by a number of authors and there are many interesting results concerning this problem (see [6, 8–24]).
In [25], Jun and Kim considered the following cubic functional equation:

It is easy to show that the function  satisfies the functional equation (1.2), which is called a cubic functional equation, and every solution of the cubic functional equation is said to be a cubic mapping.
satisfies the functional equation (1.2), which is called a cubic functional equation, and every solution of the cubic functional equation is said to be a cubic mapping.
In [26], Lee et al. considered the following quartic functional equation:

It is easy to show that the function  satisfies the functional equation (1.3), which is called a quartic functional equation and every solution of the quartic functional equation is said to be a quartic mapping.
satisfies the functional equation (1.3), which is called a quartic functional equation and every solution of the quartic functional equation is said to be a quartic mapping.
The study of stability of functional equations is important problem in nonlinear sciences and application in solving integral equation via VIM [27–29] PDE and ODE [30–34]. Let  be a set A function
be a set A function  is called a generalized metric on
is called a generalized metric on  if
if  satisfies
satisfies
(1) if and only if
if and only if  ;
;
(2) for all
for all  ;
;
(3) for all
for all  .
.
We recall a fundamental result in fixed point theory.
Let  be a complete generalized metric space and let
be a complete generalized metric space and let  be a strictly contractive mapping with Lipschitz constant
be a strictly contractive mapping with Lipschitz constant  . Then for each given element
. Then for each given element  , either
, either

for all nonnegative integers  or there exists a positive integer
or there exists a positive integer  such that
such that
(1) , for all
, for all  ;
;
(2)the sequence  converges to a fixed point
converges to a fixed point  of
of  ;
;
(3) is the unique fixed point of
is the unique fixed point of  in the set
in the set  ;
;
(4) for all
for all  .
.
In 1996, Isac and Th. M. Rassias [37] were the first to provide applications of stability theory of functional equations for the proof of new fixed point theorems with applications. By using fixed point methods, the stability problems of several functional equations have been extensively investigated by a number of authors (see [38–43]).
2. Preliminaries
The theory of random normed spaces (RN-spaces) is important as a generalization of deterministic result of linear normed spaces and also in the study of random operator equations. The RN-spaces may also provide us the appropriate tools to study the geometry of nuclear physics and have important application in quantum particle physics. The generalized Hyers-Ulam stability of different functional equations in random normed spaces, RN-spaces and fuzzy normed spaces has been recently studied by Alsina [44], Mirmostafaee and Moslehian [45] and Mirzavaziri and Moslehian [40], Miheţ and Radu [46], Miheţ et al. [47, 48], Baktash et al. [49], and Saadati et al. [50].
Let  be a complete lattice, that is, a partially ordered set in which every nonempty subset admits supremum and infimum, and
be a complete lattice, that is, a partially ordered set in which every nonempty subset admits supremum and infimum, and  ,
,  . The space of latticetic random distribution functions, denoted by
. The space of latticetic random distribution functions, denoted by  , is defined as the set of all mappings
, is defined as the set of all mappings  such that
such that  is left continuous and nondecreasing on
is left continuous and nondecreasing on  ,
,  .
.
 is defined as
is defined as  , where
, where  denotes the left limit of the function
denotes the left limit of the function  at the point
at the point  . The space
. The space  is partially ordered by the usual point-wise ordering of functions, that is,
is partially ordered by the usual point-wise ordering of functions, that is,  if and only if
if and only if  for all
for all  in
in  . The maximal element for
. The maximal element for  in this order is the distribution function given by
in this order is the distribution function given by

Definition 2.1 (see [51]).
A triangular norm ( -norm) on
-norm) on  is a mapping
is a mapping  satisfying the following conditions:
satisfying the following conditions:
(a) (boundary condition);
(boundary condition);
(b) (commutativity);
(commutativity);
(c) (associativity);
(associativity);
(d) and
and  (monotonicity).
(monotonicity).
Let  be a sequence in
be a sequence in  which converges to
which converges to  (equipped order topology). The
(equipped order topology). The  -norm
-norm  is said to be a continuous
is said to be a continuous -norm if
-norm if

for all  .
.
A  -norm
-norm  can be extended (by associativity) in a unique way to an
can be extended (by associativity) in a unique way to an  -array operation taking for
-array operation taking for  the value
the value  defined by
defined by

 can also be extended to a countable operation taking for any sequence
can also be extended to a countable operation taking for any sequence  in
in  the value
the value

The limit on the right side of (2.4) exists since the sequence  is nonincreasing and bounded from below.
is nonincreasing and bounded from below.
Note that we put  whenever
whenever  . If
. If  is a
is a  -norm then
-norm then  is defined for all
is defined for all  and
and  by 1, if
by 1, if  and
and  , if
, if  . A
. A  -norm
-norm  is said to be of Hadžić-type (we denote by
is said to be of Hadžić-type (we denote by  ) if the family
) if the family  is equicontinuous at
is equicontinuous at  (cf. [52]).
(cf. [52]).
Definition 2.2 (see [51]).
A continuous  -norm
-norm  on
on  is said to be continuous
is said to be continuous -representable if there exist a continuous
-representable if there exist a continuous  -norm
-norm  and a continuous
and a continuous  -conorm
-conorm  on
on  such that, for all
such that, for all  ,
,  ,
,

For example,

for all  ,
,  are continuous
are continuous  -representable.
-representable.
Define the mapping  from
from  to
to  by
by

Recall (see [52, 53]) that if  is a given sequence in
is a given sequence in  ,
,  is defined recurrently by
is defined recurrently by  and
and  for
for  .
.
A negation on  is any decreasing mapping
is any decreasing mapping  satisfying
satisfying  and
and  . If
. If  , for all
, for all  , then
, then  is called an involutive negation. In the following,
is called an involutive negation. In the following,  is endowed with a (fixed) negation
is endowed with a (fixed) negation  .
.
Definition 2.3.
A latticetic random normed space is a triple  , where
, where  is a vector space and
is a vector space and  is a mapping from
is a mapping from  into
into  such that the following conditions hold:
such that the following conditions hold:
(LRN1) for all
for all  if and only if
if and only if  ;
;
(LRN2) for all
for all  in
in  ,
,  and
and  ;
;
(LRN3) for all
for all  and
and  .
.
We note that from (LPN2) it follows that  .
.
Example 2.4.
Let  and operation
and operation  be defined by
be defined by

Then  is a complete lattice (see [51]). In this complete lattice, we denote its units by
is a complete lattice (see [51]). In this complete lattice, we denote its units by  and
and  . Let
. Let  be a normed space. Let
be a normed space. Let  for all
for all  ,
,  and
and  be a mapping defined by
be a mapping defined by

Then  is a latticetic random normed space.
is a latticetic random normed space.
If  is a latticetic random normed space, then
is a latticetic random normed space, then

is a complete system of neighborhoods of null vector for a linear topology on  generated by the norm
generated by the norm  .
.
Definition 2.5.
Let  be a latticetic random normed space.
be a latticetic random normed space.
(1)A sequence  in
in  is said to be convergent to
is said to be convergent to  in
in  if, for every
if, for every  and
and  , there exists a positive integer
, there exists a positive integer  such that
such that  whenever
whenever  .
.
(2)A sequence  in
in  is called Cauchy sequence if, for every
is called Cauchy sequence if, for every  and
and  , there exists a positive integer
, there exists a positive integer  such that
such that  whenever
whenever  .
.
(3)A latticetic random normed spaces  is said to be complete if and only if every Cauchy sequence in
is said to be complete if and only if every Cauchy sequence in  is convergent to a point in
is convergent to a point in  .
.
Theorem 2.6.
If  is a latticetic random normed space and
is a latticetic random normed space and  is a sequence such that
is a sequence such that  , then
, then  .
.
Proof.
The proof is the same as classical random normed spaces, see [54].
Lemma 2.7.
Let  be a latticetic random normed space and
be a latticetic random normed space and  . If
. If

then  and
and  .
.
Proof.
Let  for all
for all  . Since
. Since  , we have
, we have  , and by (LRN1) we conclude that
, and by (LRN1) we conclude that  .
.
3. Generalized Hyers-Ulam Stability of the Functional Equation (1.1): An Odd Case
One can easily show that an even mapping  satisfies (1.1) if and only if the even mapping
satisfies (1.1) if and only if the even mapping  is a quartic mapping, that is,
is a quartic mapping, that is,

and that an odd mapping  satisfies (1.1) if and only if the odd mapping
satisfies (1.1) if and only if the odd mapping  is an additive-cubic mapping, that is,
is an additive-cubic mapping, that is,

It was shown in Lemma 2.2 of [55] that  and
and  are cubic and additive, respectively, and that
are cubic and additive, respectively, and that  .
.
For a given mapping  , we define
, we define

for all  .
.
Using the fixed point method, we prove the generalized Hyers-Ulam stability of the functional equation  in complete LRN-spaces: an odd case.
in complete LRN-spaces: an odd case.
Theorem 3.1.
Let  be a linear space,
be a linear space,  a complete LRN-space and
a complete LRN-space and  a mapping from
a mapping from  to
to  is denoted by
is denoted by  such that, for some
such that, for some  ,
,

Let  be an odd mapping satisfying
be an odd mapping satisfying

for all  and all
and all  . Then
. Then

exists for each  and defines a cubic mapping
and defines a cubic mapping  such that
such that

for all  and all
and all  .
.
Proof.
Letting  in (3.5), we get
in (3.5), we get

for all  and all
and all  .
.
Replacing  by
by  in (3.5), we get
in (3.5), we get

for all  and all
and all  .
.
By (3.8) and (3.9),

for all  and all
and all  . Letting
. Letting  and
and  for all
for all  , we get
, we get

for all  and all
and all  .
.
Consider the set

and introduce the generalized metric on  :
:

where, as usual,  . It is easy to show that
. It is easy to show that  is complete. (See the proof of Lemma 2.1 of [46].)
is complete. (See the proof of Lemma 2.1 of [46].)
Now we consider the linear mapping  such that
such that

for all  .
.
Let  be given such that
be given such that  . Then
. Then

for all  and all
and all  . Hence
. Hence

for all  and all
and all  . So
. So  implies that
implies that

This means that

for all  .
.
It follows from (3.11) that

for all  and all
and all  . So
. So

By Theorem 1.1, there exists a mapping  satisfying the following:
satisfying the following:
(1) is a fixed point of
is a fixed point of  , that is,
, that is,

for all  . Since
. Since  is odd,
is odd,  is an odd mapping. The mapping
is an odd mapping. The mapping  is a unique fixed point of
is a unique fixed point of  in the set
in the set

This implies that  is a unique mapping satisfying (3.21) such that there exists a
is a unique mapping satisfying (3.21) such that there exists a  satisfying
satisfying

for all  and all
and all  ;
;
(2) as
as  . This implies the equality
. This implies the equality

for all  ;
;
(3) , which implies the inequality
, which implies the inequality

This implies that inequality (3.7) holds.
From  , by (3.5), we deduce that
, by (3.5), we deduce that

and so, by (LRN3) and (3.4), we obtain

It follows that

for all  , all
, all  and all
and all  . Since
. Since  ,
,

for all  and all
and all  . Then
. Then

for all  and all
and all  . Thus the mapping
. Thus the mapping  is cubic, as desired.
is cubic, as desired.
Corollary 3.2.
Let  and let
and let  be a real number with
be a real number with  . Let
. Let  be a normed vector space with norm
be a normed vector space with norm  and let
and let  be an LRN-space in which
be an LRN-space in which  and
and  . Let
. Let  be an odd mapping satisfying
be an odd mapping satisfying

for all  and all
and all  . Then
. Then

exists for each  and defines a cubic mapping
and defines a cubic mapping  such that
such that

for all  and all
and all  .
.
Proof.
The proof follows from Theorem 3.1 by taking

for all  . Then we can choose
. Then we can choose  and we get the desired result.
and we get the desired result.
Theorem 3.3.
Let  be a linear space,
be a linear space,  a complete LRN-space and
a complete LRN-space and  a mapping from
a mapping from  to
to  is denoted by
is denoted by  such that, for some
such that, for some  ,
,

Let  be an odd mapping satisfying (1.1). Then
be an odd mapping satisfying (1.1). Then

exists for each  and defines a cubic mapping
and defines a cubic mapping  such that
such that

for all  and all
and all  .
.
Proof.
Let  be the generalized metric space defined in the proof of Theorem 3.1.
be the generalized metric space defined in the proof of Theorem 3.1.
Consider the linear mapping  such that
such that

for all  .
.
Let  be given such that
be given such that  . Then
. Then

for all  and all
and all  . Hence
. Hence

for all  and all
and all  . So
. So  implies that
implies that

This means that

for all  .
.
It follows from (3.11) that

for all  and all
and all  . So
. So  .
.
By Theorem 1.1, there exists a mapping  satisfying the following:
satisfying the following:
(1) is a fixed point of
is a fixed point of  , that is,
, that is,

for all  . Since
. Since  is odd,
is odd,  is an odd mapping. The mapping
is an odd mapping. The mapping  is a unique fixed point of
is a unique fixed point of  in the set
in the set

This implies that  is a unique mapping satisfying (3.44) such that there exists a
is a unique mapping satisfying (3.44) such that there exists a  satisfying
satisfying

for all  and all
and all  ;
;
(2) as
as  . This implies the equality
. This implies the equality

for all  ;
;
(3) , which implies the inequality
, which implies the inequality

This implies that inequality (3.37) holds.
The rest of the proof is similar to the proof of Theorem 3.1.
Corollary 3.4.
Let  , and let
, and let  be a real number with
be a real number with  . Let
. Let  be a normed vector space with norm
be a normed vector space with norm  , and let
, and let  be an LRN-space in which
be an LRN-space in which  and
and  . Let
. Let  be an odd mapping satisfying (3.31). Then
be an odd mapping satisfying (3.31). Then

exists for each  and defines a cubic mapping
and defines a cubic mapping  such that
such that

for all  and all
and all  .
.
Proof.
The proof follows from Theorem 3.3 by taking

for all  . Then we can choose
. Then we can choose  , and we get the desired result.
, and we get the desired result.
Theorem 3.5.
Let  be a linear space,
be a linear space,  an LRN-space and let
an LRN-space and let  be a mapping from
be a mapping from  to
to  is denoted by
is denoted by  such that, for some
such that, for some  ,
,

Let  be an odd mapping satisfying (3.5). Then
be an odd mapping satisfying (3.5). Then

exists for each  and defines an additive mapping
and defines an additive mapping  such that
such that

for all  and all
and all  .
.
Proof.
Let  be the generalized metric space defined in the proof of Theorem 3.1.
be the generalized metric space defined in the proof of Theorem 3.1.
Letting  and
and  for all
for all  in (3.10), we get
in (3.10), we get

for all  and all
and all  .
.
Now we consider the linear mapping  such that
such that

for all  .
.
Let  be given such that
be given such that  . Then
. Then

for all  and all
and all  . Hence
. Hence

for all  and all
and all  . So
. So  implies that
implies that  . This means that
. This means that

for all  .
.
It follows from (3.55) that

for all  and all
and all  . So
. So  .
.
By Theorem 1.1, there exists a mapping  satisfying the following:
satisfying the following:
(1) is a fixed point of
is a fixed point of  , that is,
, that is,

for all  . Since
. Since  is odd,
is odd,  is an odd mapping. The mapping
is an odd mapping. The mapping  is a unique fixed point of
is a unique fixed point of  in the set
in the set

This implies that  is a unique mapping satisfying (3.61) such that there exists a
is a unique mapping satisfying (3.61) such that there exists a  satisfying
satisfying

for all  and all
and all  ;
;
(2) as
as  . This implies the equality
. This implies the equality

for all  ;
;
(3) , which implies the inequality
, which implies the inequality

This implies that inequality (3.54) holds.
The rest of the proof is similar to the proof of Theorem 3.1.
Corollary 3.6.
Let  , and let
, and let  be a real number with
be a real number with  . Let
. Let  be a normed vector space with norm
be a normed vector space with norm  , and let
, and let  be an LRN-space in which
be an LRN-space in which  and
and  . Let
. Let  be an odd mapping satisfying (3.31). Then
be an odd mapping satisfying (3.31). Then

exists for each  and defines an additive mapping
and defines an additive mapping  such that
such that

for all  and all
and all  .
.
Proof.
The proof follows from Theorem 3.5 by taking

for all  . Then we can choose
. Then we can choose  and we get the desired result.
and we get the desired result.
Theorem 3.7.
Let  be a linear space,
be a linear space,  an LRN-space and let
an LRN-space and let  be a mapping from
be a mapping from  to
to  is denoted by
is denoted by  such that, for some
such that, for some  ,
,

Let  be an odd mapping satisfying (3.5). Then
be an odd mapping satisfying (3.5). Then

exists for each  and defines an additive mapping
and defines an additive mapping  such that
such that

for all  and all
and all  .
.
Proof.
Let  be the generalized metric space defined in the proof of Theorem 3.1.
be the generalized metric space defined in the proof of Theorem 3.1.
Consider the linear mapping  such that
such that

for all  .
.
Let  be given such that
be given such that  . Then
. Then

for all  and all
and all  . Hence
. Hence

for all  and all
and all  . So
. So  implies that
implies that

This means that

for all  .
.
It follows from (3.55) that

for all  and all
and all  . So
. So  .
.
By Theorem 1.1, there exists a mapping  satisfying the following:
satisfying the following:
(1) is a fixed point of
is a fixed point of  , that is,
, that is,

for all  . Since
. Since  is odd,
is odd,  is an odd mapping. The mapping
is an odd mapping. The mapping  is a unique fixed point of
is a unique fixed point of  in the set
in the set

This implies that  is a unique mapping satisfying (3.78) such that there exists a
is a unique mapping satisfying (3.78) such that there exists a  satisfying
satisfying

for all  and all
and all  ;
;
(2) as
as  . This implies the equality
. This implies the equality

for all  ;
;
(3) , which implies the inequality
, which implies the inequality

This implies that inequality (3.71) holds.
The rest of the proof is similar to the proof of Theorem 3.1.
Corollary 3.8.
Let  , and let
, and let  be a real number with
be a real number with  . Let
. Let  be a normed vector space with norm
be a normed vector space with norm  , and let
, and let  be an LRN-space in which
be an LRN-space in which  and
and  . Let
. Let  be an odd mapping satisfying (3.31). Then
be an odd mapping satisfying (3.31). Then

exists for each  and defines an additive mapping
and defines an additive mapping  such that
such that

for all  and all
and all  .
.
Proof.
The proof follows from Theorem 3.7 by taking

for all  . Then we can choose
. Then we can choose  and we get the desired result.
and we get the desired result.
4. Generalized Hyers-Ulam Stability of the Functional Equation (1.1): An Even Case
Using the fixed point method, we prove the generalized Hyers-Ulam stability of the functional equation  in complete RN-spaces: an even case.
in complete RN-spaces: an even case.
Theorem 4.1.
Let  be a linear space,
be a linear space,  an LRN-space and let
an LRN-space and let  be a mapping from
be a mapping from  to
to  is denoted by
is denoted by  such that, for some
such that, for some  ,
,

Let  be an even mapping satisfying
be an even mapping satisfying  and (3.5). Then
and (3.5). Then

exists for each  and defines a quartic mapping
and defines a quartic mapping  such that
such that

for all  and all
and all  .
.
Proof.
Letting  in (3.5), we get
in (3.5), we get

for all  and all
and all  .
.
Letting  in (3.5), we get
in (3.5), we get

for all  and all
and all  .
.
By (4.4) and (4.5),

for all  and all
and all  .
.
Consider the set

and introduce the generalized metric on 

where, as usual,  . It is easy to show that
. It is easy to show that  is complete. (See the proof of Lemma 2.1 of [46].)
is complete. (See the proof of Lemma 2.1 of [46].)
Now we consider the linear mapping  such that
such that

for all  .
.
Let  be given such that
be given such that  . Then
. Then

for all  and all
and all  . Hence
. Hence

for all  and all
and all  . So
. So  implies that
implies that

This means that

for all  .
.
It follows from (4.6) that

for all  and all
and all  . So
. So  .
.
By Theorem 1.1, there exists a mapping  satisfying the following:
satisfying the following:
(1) is a fixed point of
is a fixed point of  , that is,
, that is,

for all  . Since
. Since  is even,
is even,  is an even mapping. The mapping
is an even mapping. The mapping  is a unique fixed point of
is a unique fixed point of  in the set
in the set

This implies that  is a unique mapping satisfying (4.15) such that there exists a
is a unique mapping satisfying (4.15) such that there exists a  satisfying
satisfying

for all  and all
and all  ;
;
(2) as
as  . This implies the equality
. This implies the equality

for all  ;
;
(3) , which implies the inequality
, which implies the inequality

This implies that inequality (4.3) holds.
The rest of the proof is similar to the proof of Theorem 3.1.
Corollary 4.2.
Let  , and let
, and let  be a real number with
be a real number with  . Let
. Let  be a normed vector space with norm
be a normed vector space with norm  , and let
, and let  be an LRN-space in which
be an LRN-space in which  and
and  . Let
. Let  be an even mapping satisfying
be an even mapping satisfying  and (3.31). Then
and (3.31). Then

exists for each  and defines a quartic mapping
and defines a quartic mapping  such that
such that

for all  and all
and all  .
.
Proof.
The proof follows from Theorem 4.1 by taking

for all  . Then we can choose
. Then we can choose  , and we get the desired result.
, and we get the desired result.
Similarly, we can obtain the following. We will omit the proof.
Theorem 4.3.
Let  be a linear space,
be a linear space,  an LRN-space and let
an LRN-space and let  be a mapping from
be a mapping from  to
to  is denoted by
is denoted by  such that, for some
such that, for some  ,
,

Let  be an even mapping satisfying
be an even mapping satisfying  and (3.5). Then
and (3.5). Then

exists for each  and defines a quartic mapping
and defines a quartic mapping  such that
such that

for all  and all
and all  .
.
Corollary 4.4.
Let  , and let
, and let  be a real number with
be a real number with  . Let
. Let  be a normed vector space with norm
be a normed vector space with norm  , and let
, and let  be an LRN-space in which
be an LRN-space in which  and
and  . Let
. Let  be an even mapping satisfying
be an even mapping satisfying  and (3.31). Then
and (3.31). Then

exists for each  and defines a quartic mapping
and defines a quartic mapping  such that
such that

for all  and all
and all  .
.
Proof.
The proof follows from Theorem 4.3 by taking

for all  . Then we can choose
. Then we can choose  , and we get the desired result.
, and we get the desired result.
References
El Naschie MS: On a fuzzy Kähler-like manifold which is consistent with the two slit experiment. International Journal of Nonlinear Sciences and Numerical Simulation 2005,6(2):95–98. 10.1515/IJNSNS.2005.6.2.95
Sigalotti LDG, Mejias A: On El Naschie's conjugate complex time, fractal space-time and faster-than-light particles. International Journal of Nonlinear Sciences and Numerical Simulation 2006,7(4):467–472. 10.1515/IJNSNS.2006.7.4.467
Ulam SM: A Collection of Mathematical Problems. Interscience Publishers, New York, NY, USA; 1960:xiii+150.
Hyers DH: On the stability of the linear functional equation. Proceedings of the National Academy of Sciences of the United States of America 1941, 27: 222–224. 10.1073/pnas.27.4.222
Aoki T: On the stability of the linear transformation in Banach spaces. Journal of the Mathematical Society of Japan 1950, 2: 64–66. 10.2969/jmsj/00210064
Rassias ThM: On the stability of the linear mapping in Banach spaces. Proceedings of the American Mathematical Society 1978,72(2):297–300. 10.1090/S0002-9939-1978-0507327-1
Găvruţa P: A generalization of the Hyers-Ulam-Rassias stability of approximately additive mappings. Journal of Mathematical Analysis and Applications 1994,184(3):431–436. 10.1006/jmaa.1994.1211
Hyers DH, Isac G, Rassias ThM: Stability of Functional Equations in Several Variables. Birkhäuser, Boston, Mass, USA; 1998:vi+313.
Jung S-M: Hyers-Ulam-Rassias Stability of Functional Equations in Mathematical Analysis. Hadronic Press, Palm Harbor, Fla, USA; 2001:ix+256.
Park C: Hyers-Ulam-Rassias stability of homomorphisms in quasi-Banach algebras. Bulletin des Sciences Mathématiques 2008,132(2):87–96.
Park C: Hyers-Ulam-Rassias stability of a generalized Apollonius-Jensen type additive mapping and isomorphisms between -algebras. Mathematische Nachrichten 2008,281(3):402–411. 10.1002/mana.200510611
Park C, Cui J: Generalized stability of -ternary quadratic mappings. Abstract and Applied Analysis 2007, 2007:-6.
Park C, Najati A: Homomorphisms and derivations in -algebras. Abstract and Applied Analysis 2007, 2007:-12.
Rassias JM: On approximation of approximately linear mappings by linear mappings. Bulletin des Sciences Mathématiques 1984,108(4):445–446.
Rassias JM: Refined Hyers-Ulam approximation of approximately Jensen type mappings. Bulletin des Sciences Mathématiques 2007,131(1):89–98.
Rassias JM, Rassias MJ: Asymptotic behavior of alternative Jensen and Jensen type functional equations. Bulletin des Sciences Mathématiques 2005,129(7):545–558.
Rassias ThM: Problem 16; 2, Report of the 27th International Symposium on Functional Equations. Aequationes Mathematicae 1990, 39: 292–293.
Rassias ThM: On the stability of the quadratic functional equation and its applications. Universitatis Babeş-Bolyai. Studia. Mathematica 1998,43(3):89–124.
Rassias ThM: The problem of S. M. Ulam for approximately multiplicative mappings. Journal of Mathematical Analysis and Applications 2000,246(2):352–378. 10.1006/jmaa.2000.6788
Rassias ThM: On the stability of functional equations in Banach spaces. Journal of Mathematical Analysis and Applications 2000,251(1):264–284. 10.1006/jmaa.2000.7046
Rassias ThM: On the stability of functional equations and a problem of Ulam. Acta Applicandae Mathematicae 2000,62(1):23–130. 10.1023/A:1006499223572
Rassias ThM, Šemrl P: On the behavior of mappings which do not satisfy Hyers-Ulam stability. Proceedings of the American Mathematical Society 1992,114(4):989–993. 10.1090/S0002-9939-1992-1059634-1
Rassias ThM, Šemrl P: On the Hyers-Ulam stability of linear mappings. Journal of Mathematical Analysis and Applications 1993,173(2):325–338. 10.1006/jmaa.1993.1070
Rassias ThM, Shibata K: Variational problem of some quadratic functionals in complex analysis. Journal of Mathematical Analysis and Applications 1998,228(1):234–253. 10.1006/jmaa.1998.6129
Jun K-W, Kim H-M: The generalized Hyers-Ulam-Rassias stability of a cubic functional equation. Journal of Mathematical Analysis and Applications 2002,274(2):267–278.
Lee SH, Im SM, Hwang IS: Quartic functional equations. Journal of Mathematical Analysis and Applications 2005,307(2):387–394. 10.1016/j.jmaa.2004.12.062
Saadati R, Vaezpour SM, Rhoades BE: -stability approach to variational iteration method for solving integral equations. Fixed Point Theory and Applications 2009, 2009:-9.
He JH: Variational iteration method—a kind of nonlinear analytical technique: some examples. International Journal of Non-Linear Mechanics 1999, 34: 699–708. 10.1016/S0020-7462(98)00048-1
He J-H: A review on some new recently developed nonlinear analytical techniques. International Journal of Nonlinear Sciences and Numerical Simulation 2000,1(1):51–70. 10.1515/IJNSNS.2000.1.1.51
He J-H, Wu X-H: Variational iteration method: new development and applications. Computers & Mathematics with Applications 2007,54(7–8):881–894. 10.1016/j.camwa.2006.12.083
He J-H: Variational iteration method—some recent results and new interpretations. Journal of Computational and Applied Mathematics 2007,207(1):3–17. 10.1016/j.cam.2006.07.009
Ozer H: Application of the variational iteration method to the boundary value problems with jump discontinuities arising in solid mechanics. International Journal of Nonlinear Sciences and Numerical Simulation 2007,8(4):513–518. 10.1515/IJNSNS.2007.8.4.513
Biazar J, Ghazvini H: He's variational iteration method for solving hyperbolic differential equations. International Journal of Nonlinear Sciences and Numerical Simulation 2007, 8: 311–314. 10.1515/IJNSNS.2007.8.3.311
Odibat ZM, Momani S: Application of variational iteration method to nonlinear differential equations of fractional order. International Journal of Nonlinear Sciences and Numerical Simulation 2006,7(1):27–34. 10.1515/IJNSNS.2006.7.1.27
Cădariu L, Radu V: Fixed points and the stability of Jensen's functional equation. Journal of Inequalities in Pure and Applied Mathematics 2003,4(1, article 4):7.
Diaz JB, Margolis B: A fixed point theorem of the alternative, for contractions on a generalized complete metric space. Bulletin of the American Mathematical Society 1968, 74: 305–309. 10.1090/S0002-9904-1968-11933-0
Isac G, Rassias ThM: Stability of -additive mappings: applications to nonlinear analysis. International Journal of Mathematics and Mathematical Sciences 1996,19(2):219–228. 10.1155/S0161171296000324
Cădariu L, Radu V: On the stability of the Cauchy functional equation: a fixed point approach. In Iteration Theory. Volume 346. Karl-Franzens-Universität Graz, Graz, Austria; 2004:43–52.
Cădariu L, Radu V: Fixed point methods for the generalized stability of functional equations in a single variable. Fixed Point Theory and Applications 2008, 2008:-15.
Mirzavaziri M, Moslehian MS: A fixed point approach to stability of a quadratic equation. Bulletin of the Brazilian Mathematical Society 2006,37(3):361–376. 10.1007/s00574-006-0016-z
Park C: Fixed points and Hyers-Ulam-Rassias stability of Cauchy-Jensen functional equations in Banach algebras. Fixed Point Theory and Applications 2007, 2007:-15.
Park C: Generalized Hyers-Ulam stability of quadratic functional equations: a fixed point approach. Fixed Point Theory and Applications 2008, 2008:-9.
Radu V: The fixed point alternative and the stability of functional equations. Fixed Point Theory 2003,4(1):91–96.
Alsina C: On the stability of a functional equation arising in probabilistic normed spaces. In General Inequalities. Volume 80. Birkhäuser, Basel, Switzerland; 1987:263–271.
Mirmostafaee AK, Moslehian MS: Fuzzy approximately cubic mappings. Information Sciences 2008,178(19):3791–3798. 10.1016/j.ins.2008.05.032
Miheţ D, Radu V: On the stability of the additive Cauchy functional equation in random normed spaces. Journal of Mathematical Analysis and Applications 2008,343(1):567–572.
Miheţ D, Saadati R, Vaezpour SM: The stability of the quartic functional equation in random normed spaces. Acta Applicandae Mathematicae 2011,110(2):797–803.
Miheţ D, Saadati R, Vaezpour SM: The stability of anadditive functional equation in Menger probabilistic -normed spaces. Mathematica Slovaca. In press
Baktash E, Cho YJ, Jalili M, Saadati R, Vaezpour SM: On the stability of cubic mappings and quadratic mappings in random normed spaces. Journal of Inequalities and Applications 2008, 2008:-11.
Saadati R, Vaezpour SM, Cho YJ: Erratumml: A note to paper "On the stability of cubic mappings and quartic mappings in random normed spaces". Journal of Inequalities and Applications 2009, 2009:-6.
Deschrijver G, Kerre EE: On the relationship between some extensions of fuzzy set theory. Fuzzy Sets and Systems 2003,133(2):227–235. 10.1016/S0165-0114(02)00127-6
Hadžić O, Pap E: Fixed Point Theory in Probabilistic Metric Spaces, Mathematics and Its Applications. Volume 536. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2001:x+273.
Hadžić O, Pap E, Budinčević M: Countable extension of triangular norms and their applications to the fixed point theory in probabilistic metric spaces. Kybernetika 2002,38(3):363–382.
Schweizer B, Sklar A: Probabilistic Metric Spaces, North-Holland Series in Probability and Applied Mathematics. North-Holland Publishing, New York, NY, USA; 1983:xvi+275.
Eshaghi-Gordji M, Kaboli-Gharetapeh S, Park C, Zolfaghri S: Stability of an additive-cubic-quartic functional equation. Advances in Difference Equations 2009, 2009: 20.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Saadati, R., Zohdi, M.M. & Vaezpour, S.M. Nonlinear 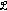 -Random Stability of an ACQ Functional Equation.
J Inequal Appl 2011, 194394 (2011). https://doi.org/10.1155/2011/194394
-Random Stability of an ACQ Functional Equation.
J Inequal Appl 2011, 194394 (2011). https://doi.org/10.1155/2011/194394
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/194394