- Research Article
- Open access
- Published:
Existence of Solutions for 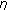 -Generalized Vector Variational-Like Inequalities
-Generalized Vector Variational-Like Inequalities
Journal of Inequalities and Applications volume 2010, Article number: 968271 (2010)
Abstract
We introduce and study a class of  -generalized vector variational-like inequalities and a class of
-generalized vector variational-like inequalities and a class of  -generalized strong vector variational-like inequalities in the setting of Hausdorff topological vector spaces. An equivalence result concerned with two classes of
-generalized strong vector variational-like inequalities in the setting of Hausdorff topological vector spaces. An equivalence result concerned with two classes of  -generalized vector variational-like inequalities is proved under suitable conditions. By using FKKM theorem, some new existence results of solutions for the
-generalized vector variational-like inequalities is proved under suitable conditions. By using FKKM theorem, some new existence results of solutions for the  -generalized vector variational-like inequalities and
-generalized vector variational-like inequalities and  -generalized strong vector variational-like inequalities are obtained under some suitable conditions.
-generalized strong vector variational-like inequalities are obtained under some suitable conditions.
1. Introduction
Vector variational inequality was first introduced and studied by Giannessi [1] in the setting of finite-dimensional Euclidean spaces. Since then, the theory with applications for vector variational inequalities, vector complementarity problems, vector equilibrium problems, and vector optimization problems have been studied and generalized by many authors (see, e.g., [2–15] and the references therein).
Recently, Yu et al. [16] considered a more general form of weak vector variational inequalities and proved some new results on the existence of solutions of the new class of weak vector variational inequalities in the setting of Hausdorff topological vector spaces.
Very recently, Ahmad and Khan [17] introduced and considered weak vector variational-like inequalities with  -generally convex mapping and gave some existence results.
-generally convex mapping and gave some existence results.
On the other hand, Fang and Huang [18] studied some existence results of solutions for a class of strong vector variational inequalities in Banach spaces, which give a positive answer to an open problem proposed by Chen and Hou [19].
In 2008, Lee et al. [20] introduced a new class of strong vector variational-type inequalities in Banach spaces. They obtained the existence theorems of solutions for the inequalities without monotonicity in Banach spaces by using Brouwer fixed point theorem and Browder fixed point theorem.
Motivated and inspired by the work mentioned above, in this paper we introduce and study a class of  -generalized vector variational-like inequalities and a class of
-generalized vector variational-like inequalities and a class of  -generalized strong vector variational-like inequalities in the setting of Hausdorff topological vector spaces. We first show an equivalence theorem concerned with two classes of
-generalized strong vector variational-like inequalities in the setting of Hausdorff topological vector spaces. We first show an equivalence theorem concerned with two classes of  -generalized vector variational-like inequalities under suitable conditions. By using FKKM theorem, we prove some new existence results of solutions for the
-generalized vector variational-like inequalities under suitable conditions. By using FKKM theorem, we prove some new existence results of solutions for the  -generalized vector variational-like inequalities and
-generalized vector variational-like inequalities and  -generalized strong vector variational-like inequalities under some suitable conditions. The results presented in this paper improve and generalize some known results due to Ahmad and Khan [17], Lee et al. [20], and Yu et al. [16].
-generalized strong vector variational-like inequalities under some suitable conditions. The results presented in this paper improve and generalize some known results due to Ahmad and Khan [17], Lee et al. [20], and Yu et al. [16].
2. Preliminaries
Let  and
and  be two real Hausdorff topological vector spaces,
be two real Hausdorff topological vector spaces,  a nonempty, closed, and convex subset, and
a nonempty, closed, and convex subset, and  a closed, convex, and pointed cone with apex at the origin. Recall that the Hausdorff topological vector space
a closed, convex, and pointed cone with apex at the origin. Recall that the Hausdorff topological vector space  is said to an ordered Hausdorff topological vector space denoted by
is said to an ordered Hausdorff topological vector space denoted by  if ordering relations are defined in
if ordering relations are defined in  as follows:
as follows:

If the interior  is nonempty, then the weak ordering relations in
is nonempty, then the weak ordering relations in  are defined as follows:
are defined as follows:

Let  be the space of all continuous linear maps from
be the space of all continuous linear maps from  to
to  and
and  . We denote the value of
. We denote the value of  on
on  by
by  . Throughout this paper, we assume that
. Throughout this paper, we assume that  is a family of closed, convex, and pointed cones of
is a family of closed, convex, and pointed cones of  such that
such that  for all
for all  ,
,  is a mapping from
is a mapping from  into
into  , and
, and  is a mapping from
is a mapping from  into
into  .
.
In this paper, we consider the following two kinds of vector variational inequalities:

-Generalized Vector Variational-Like Inequality (for short,  -GVVLI): for each
-GVVLI): for each  and
and  , find
, find  such that
such that


-Generalized Strong Vector Variational-Like Inequality (for short,  -GSVVLI): for each
-GSVVLI): for each  and
and  , find
, find  such that
such that


-GVVLI and  -GSVVLI encompass many models of variational inequalities. For example, the following problems are the special cases of
-GSVVLI encompass many models of variational inequalities. For example, the following problems are the special cases of  -GVVLI and
-GVVLI and  -GSVVLI.
-GSVVLI.
( ) If
) If  and
and  for all
for all  , then
, then  -GVVLI reduces to finding
-GVVLI reduces to finding  , such that for each
, such that for each  ,
, 

which is introduced and studied by Ahmad and Khan [17]. In addition, if  for each
for each  , then
, then  -GVVLI reduces to the following model studied by Yu et al. [16].
-GVVLI reduces to the following model studied by Yu et al. [16].
Find  such that for each
such that for each  ,
, 

( ) If
) If  and
and  for all
for all  , then
, then  -GSVVLI is equivalent to the following vector variational inequality problem introduced and studied by Lee et al. [20].
-GSVVLI is equivalent to the following vector variational inequality problem introduced and studied by Lee et al. [20].
Find  satisfying
satisfying

For our main results, we need the following definitions and lemmas.
Definition 2.1.
Let  and
and  be two mappings and
be two mappings and  .
.  is said to be
is said to be  -monotone in
-monotone in  if and only if
if and only if

Definition 2.2.
Let  and
and  be two mappings. We say that
be two mappings. We say that  is
is  -hemicontinuous if, for any given
-hemicontinuous if, for any given  and
and  , the mapping
, the mapping  is continuous at
is continuous at  .
.
Definition 2.3.
A multivalued mapping  is said to be upper semicontinuous on
is said to be upper semicontinuous on  if, for all
if, for all  and for each open set
and for each open set  in
in  with
with  , there exists an open neighbourhood
, there exists an open neighbourhood  of
of  such that
such that  for all
for all  .
.
Lemma 2.4 (see [21]).
Let  be an ordered topological vector space with a closed, pointed, and convex cone
be an ordered topological vector space with a closed, pointed, and convex cone  with
with  . Then for any
. Then for any  , we have
, we have
(1) and
and  imply
imply  ;
;
(2) and
and  imply
imply  ;
;
(3) and
and  imply
imply  ;
;
(4) and
and  imply
imply  .
.
Lemma 2.5 (see [22]).
Let  be a nonempty, closed, and convex subset of a Hausdorff topological space, and
be a nonempty, closed, and convex subset of a Hausdorff topological space, and  a multivalued map. Suppose that for any finite set
a multivalued map. Suppose that for any finite set  , one has
, one has  (i.e.,
(i.e.,  is a KKM mapping) and
is a KKM mapping) and  is closed for each
is closed for each  and compact for some
and compact for some  , where
, where  denotes the convex hull operator. Then
denotes the convex hull operator. Then  .
.
Lemma 2.6 (see [23]).
Let  be a Hausdorff topological space,
be a Hausdorff topological space,  be nonempty compact convex subsets of
be nonempty compact convex subsets of  . Then
. Then  is compact.
is compact.
Lemma 2.7 (see [24]).
Let  and
and  be two topological spaces. If
be two topological spaces. If  is upper semicontinuous with closed values, then
is upper semicontinuous with closed values, then  is closed.
is closed.
3. Main Results
Theorem 3.1.
Let  be a Hausdorff topological linear space,
be a Hausdorff topological linear space,  a nonempty, closed, and convex subset, and
a nonempty, closed, and convex subset, and  an ordered topological vector space with
an ordered topological vector space with  for all
for all  . Let
. Let  and
and  be affine mappings such that
be affine mappings such that  for each
for each  . Let
. Let  be an
be an  -hemicontinuous mapping. If
-hemicontinuous mapping. If  and
and  is
is  -monotone in
-monotone in  then for each
then for each  ,
,  , the following statements are equivalent
, the following statements are equivalent
(i)find  , such that
, such that  , for all
, for all 
(ii)find  , such that
, such that  , for all
, for all 
where  is defined by
is defined by  for all
for all  .
.
Proof.
Suppose that (i) holds. We can find  , such that
, such that

Since  is
is  -monotone, for each
-monotone, for each  we have
we have

On the other hand, we know  is affine and
is affine and  . It follows that
. It follows that

Hence  is also
is also  -monotone. That is
-monotone. That is

Since  , for all
, for all  , we obtain
, we obtain

By Lemma 2.4,

and so  is a solution of (ii).
is a solution of (ii).
Conversely, suppose that (ii) holds. Then there exists  such that
such that

For each  ,
,  , we let
, we let  . Obviously,
. Obviously,  . It follows that
. It follows that

Since  and
and  are affine and
are affine and  , we have
, we have

That is

Considering the  -hemicontinuity of
-hemicontinuity of  and letting
and letting  , we have
, we have

This completes the proof.
Remark 3.2.
If  and
and  for all
for all  , then Theorem 3.1 is reduced to Lemma
, then Theorem 3.1 is reduced to Lemma  of [17].
of [17].
Let  be a closed convex subset of a topological linear space
be a closed convex subset of a topological linear space  and
and  a family of closed, convex, and pointed cones of a topological space
a family of closed, convex, and pointed cones of a topological space  such that
such that  for all
for all  . Throughout this paper, we define a set-valued mapping
. Throughout this paper, we define a set-valued mapping  as follows:
as follows:

Theorem 3.3.
Let  be a Hausdorff topological linear space,
be a Hausdorff topological linear space,  a nonempty, closed, compact, and convex subset, and
a nonempty, closed, compact, and convex subset, and  an ordered topological vector space with
an ordered topological vector space with  for all
for all  . Let
. Let  and
and  be affine mappings such that
be affine mappings such that  for each
for each  . Let
. Let  be an
be an  -hemicontinuous mapping. Assume that the following conditions are satisfied
-hemicontinuous mapping. Assume that the following conditions are satisfied
(i) and
and  is
is  -monotone in
-monotone in  ;
;
(ii) is an upper semicontinuous set-valued mapping.
is an upper semicontinuous set-valued mapping.
Then for each  ,
,  , there exist
, there exist  such that
such that

Proof.
For each  , we denote
, we denote  and define
and define

Then  and
and  are nonempty since
are nonempty since  and
and  . The proof is divided into the following three steps.
. The proof is divided into the following three steps.
-
(I)
First, we prove the following conclusion:
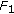 is a KKM mapping. Indeed, assume that
is a KKM mapping. Indeed, assume that 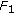 is not a KKM mapping; then there exist
is not a KKM mapping; then there exist 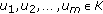 ,
, 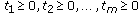 with
with 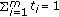 and
and  such that
such that 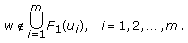 (3.15)
(3.15)
That is,

Since  and
and  are affine, we have
are affine, we have

On the other hand, we know  . Then we have
. Then we have  . It is impossible and so
. It is impossible and so  is a KKM mapping.
is a KKM mapping.
-
(II)
Further, we prove that
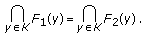 (3.18)
(3.18)
In fact, if  , then
, then  From the proof of Theorem 3.1, we know that
From the proof of Theorem 3.1, we know that  is
is  -monotone in
-monotone in  . It follows that
. It follows that

and so

By Lemma 2.4, we have

and so  for each
for each  . That is,
. That is,  and so
and so

Conversely, suppose that  Then
Then

It follows from Theorem 3.1 that

That is,  and so
and so

which implies that

( ) Last, we prove that
) Last, we prove that  Indeed, since
Indeed, since  is a KKM mapping, we know that, for any finite set
is a KKM mapping, we know that, for any finite set  one has
one has

This shows that  is also a KKM mapping.
is also a KKM mapping.
Now, we prove that  is closed for all
is closed for all  . Assume that there exists a net
. Assume that there exists a net  with
with  . Then
. Then

Using the definition of  , we have
, we have

Since  and
and  are continuous, it follows that
are continuous, it follows that

Since  is upper semicontinuous mapping with close values, by Lemma 2.7, we know that
is upper semicontinuous mapping with close values, by Lemma 2.7, we know that  is closed, and so
is closed, and so

This implies that

and so  is closed. Considering the compactness of
is closed. Considering the compactness of  and closeness of
and closeness of  , we know that
, we know that  is compact. By Lemma 2.5, we have
is compact. By Lemma 2.5, we have  and it follows that
and it follows that  , that is, for each
, that is, for each  and
and  there exists
there exists  such that
such that

Thus,  -GVVLI is solvable. This completes the proof.
-GVVLI is solvable. This completes the proof.
Remark 3.4.
The condition (ii) in Theorem 3.3 can be found in several papers (see, e.g., [25, 26]).
Remark 3.5.
If  and
and  for all
for all  in Theorem 3.3, then condition (ii) holds and condition (i) is equivalent to the
in Theorem 3.3, then condition (ii) holds and condition (i) is equivalent to the  -monotonicity of
-monotonicity of  . Thus, it is easy to see that Theorem 3.3 is a generalization of [17, Theorem
. Thus, it is easy to see that Theorem 3.3 is a generalization of [17, Theorem  ].
].
In the above theorem,  is compact. In the following theorem, under some suitable conditions, we prove a new existence result of solutions for
is compact. In the following theorem, under some suitable conditions, we prove a new existence result of solutions for  -GVVLI without the compactness of
-GVVLI without the compactness of  .
.
Theorem 3.6.
Let  be a Hausdorff topological linear space,
be a Hausdorff topological linear space,  a nonempty, closed, and convex subset, and
a nonempty, closed, and convex subset, and  be an ordered topological vector space with
be an ordered topological vector space with  for all
for all  . Let
. Let  and
and  be affine mappings such that
be affine mappings such that  for each
for each  . Let
. Let  be an
be an  -hemicontinuous mapping. Assume that the following conditions are satisfied:
-hemicontinuous mapping. Assume that the following conditions are satisfied:
(i) and
and  is
is  -monotone in
-monotone in  ;
;
(ii) is an upper semicontinuous set-valued mapping;
is an upper semicontinuous set-valued mapping;
(iii)there exists a nonempty compact and convex subset  of
of  and for each
and for each  ,
,  ,
,  , there exist
, there exist  such that
such that

Then for each  ,
,  , there exist
, there exist  such that
such that

Proof.
By Theorem 3.1, we know that the solution set of the problem (ii) in Theorem 3.1 is equivalent to the solution set of following variational inequality: find  , such that
, such that

For each  and
and  we denote
we denote  Let
Let  be defined as follows:
be defined as follows:

Obviously, for each  ,
,

Using the proof of Theorem 3.3, we obtain that  is a closed subset of
is a closed subset of  . Considering the compactness of
. Considering the compactness of  and closedness of
and closedness of  , we know that
, we know that  is compact.
is compact.
Now we prove that for any finite set  , one has
, one has  Let
Let  Since
Since  is a real Hausdorff topological vector space, for each
is a real Hausdorff topological vector space, for each  ,
,  is compact and convex. Let
is compact and convex. Let  . By Lemma 2.6, we know that
. By Lemma 2.6, we know that  is a compact and convex subset of
is a compact and convex subset of  .
.
Let  be defined as follows:
be defined as follows:

Using the proof of Theorem 3.3, we obtain

and so there exists 
Next we prove that  . In fact, if
. In fact, if  then the assumption implies that there exists
then the assumption implies that there exists  such that
such that

which contradicts  and so
and so  .
.
Since  and
and  for each
for each  , it follows that
, it follows that  . Thus, for any finite set
. Thus, for any finite set  , we have
, we have  Considering the compactness of
Considering the compactness of  for each
for each  , we know that there exists
, we know that there exists  such that
such that  Therefore, the solution set of
Therefore, the solution set of  -GVVLI is nonempty. This completes the proof.
-GVVLI is nonempty. This completes the proof.
In the following, we prove the solvability of  -GSVVLI under some suitable conditions by using FKKM theorem.
-GSVVLI under some suitable conditions by using FKKM theorem.
Theorem 3.7.
Let  be a Hausdorff topological linear space,
be a Hausdorff topological linear space,  a nonempty, closed, and convex set, and
a nonempty, closed, and convex set, and  an ordered Hausdorff topological vector space with
an ordered Hausdorff topological vector space with  for all
for all  . Assume that for each
. Assume that for each  and
and  are affine,
are affine,  and
and  for all
for all  . Let
. Let  be a mapping such that
be a mapping such that
(i)for each  ,
,  the set
the set  is open in
is open in 
(ii)there exists a nonempty compact and convex subset  of
of  and for each
and for each  ,
,  ,
,  there exists
there exists  such that
such that

Then for each  ,
,  there exists
there exists  such that
such that

Proof.
For each  and
and  we denote
we denote  . Let
. Let  be defined as follows:
be defined as follows:

Obviously, for each  ,
,

Since  is a closed subset of
is a closed subset of  , considering the compactness of
, considering the compactness of  and closedness of
and closedness of  , we know that
, we know that  is compact.
is compact.
Now we prove that for any finite set  , one has
, one has  Let
Let  Since
Since  is a real Hausdorff topological vector space, for each
is a real Hausdorff topological vector space, for each  ,
,  is compact and convex. Let
is compact and convex. Let  . By Lemma 2.6, we know that
. By Lemma 2.6, we know that  is a compact and convex subset of
is a compact and convex subset of  .
.
Let  be defined as follows:
be defined as follows:

We claim that  is a KKM mapping. Indeed, assume that
is a KKM mapping. Indeed, assume that  is not a KKM mapping. Then there exist
is not a KKM mapping. Then there exist  ,
,  with
with  and
and  such that
such that

That is,

Since  and
and  are affine, we have
are affine, we have

On the other hand, we know  and so
and so

which is impossible. Therefore,  is a KKM mapping.
is a KKM mapping.
Since  is a closed subset of
is a closed subset of  , it follows that
, it follows that  is compact. By Lemma 2.5, we have
is compact. By Lemma 2.5, we have

Thus, there exists 
Next we prove that  . In fact, if
. In fact, if  then the condition (ii) implies that there exists
then the condition (ii) implies that there exists  such that
such that

which contradicts  and so
and so  .
.
Since  and
and  for each
for each  , it follows that
, it follows that  . Thus, for any finite set
. Thus, for any finite set  , we have
, we have  Considering the compactness of
Considering the compactness of  for each
for each  , it is easy to know that there exists
, it is easy to know that there exists  such that
such that  Therefore, for each
Therefore, for each  ,
,  there exists
there exists  such that
such that

Thus,  -GSVVI is solvable. This completes the proof.
-GSVVI is solvable. This completes the proof.
Remark 3.8.
If  is compact,
is compact,  , and
, and  , then Theorem 3.7 is reduced to Theorem
, then Theorem 3.7 is reduced to Theorem  in [20].
in [20].
References
Giannessi F: Theorems of alternative, quadratic programs and complementarity problems. In Variational Inequalities and Complementarity Problems. Edited by: Cottle RW, Giannessi F, Lions JL. John Wiley & Sons, New York, NY, USA; 1980:151–186.
Chen G-Y, Huang XX, Yang XQ: Vector Optimization: Set-Valued and Variational Analysis, Lecture Notes in Economics and Mathematical Systems. Volume 541. Springer, Berlin, Germany; 2005:x+306.
Fang Y-P, Huang NJ: Feasibility and solvability of vector variational inequalities with moving cones in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(5):2024–2034. 10.1016/j.na.2008.02.100
Giannessi F (Ed): Vector Variational Inequalities and Vector Equilibrium, Nonconvex Optimization and Its Applications. Volume 38. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2000:xiv+523.
Göpfert A, Riahi H, Tammer C, Zǎlinescu C: Variational Methods in Partially Ordered Spaces, CMS Books in Mathematics. Springer, New York, NY, USA; 2003:xiv+350.
Guu S-M, Huang N-J, Li J: Scalarization approaches for set-valued vector optimization problems and vector variational inequalities. Journal of Mathematical Analysis and Applications 2009, 356(2):564–576. 10.1016/j.jmaa.2009.03.040
Huang NJ, Gao CJ: Some generalized vector variational inequalities and complementarity problems for multivalued mappings. Applied Mathematics Letters 2003, 16(7):1003–1010. 10.1016/S0893-9659(03)90087-5
Huang NJ, Li J, Thompson HB: Generalized vector -variational inequalities and vector -complementarity problems for point-to-set mappings. Mathematical and Computer Modelling 2008, 48(5–6):908–917. 10.1016/j.mcm.2006.01.030
Huang NJ, Long XJ, Zhao CW: Well-posedness for vector quasi-equilibrium problems with applications. Journal of Industrial and Management Optimization 2009, 5(2):341–349.
Huang NJ, Rubinov AM, Yang XQ: Vector optimization problems with nonconvex preferences. Journal of Global Optimization 2008, 40(4):765–777. 10.1007/s10898-006-9113-1
Huang NJ, Yang XQ, Chan WK: Vector complementarity problems with a variable ordering relation. European Journal of Operational Research 2007, 176(1):15–26. 10.1016/j.ejor.2005.06.046
Isac G, Bulavsky VA, Kalashnikov VV: Complementarity, Equilibrium, Efficiency and Economics, Nonconvex Optimization and Its Applications. Volume 63. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2002:xviii+445.
Li J, Huang NJ, Kim JK: On implicit vector equilibrium problems. Journal of Mathematical Analysis and Applications 2003, 283(2):501–512. 10.1016/S0022-247X(03)00277-4
Long XJ, Huang NJ, Teo KL: Existence and stability of solutions for generalized strong vector quasi-equilibrium problem. Mathematical and Computer Modelling 2008, 47(3–4):445–451. 10.1016/j.mcm.2007.04.013
Zhong RY, Huang NJ, Wong MM: Connectedness and path-connectedness of solution sets to symmetric vector equilibrium problems. Taiwanese Journal of Mathematics 2009, 13(2):821–836.
Yu M, Wang SY, Fu WT, Xiao W-S: On the existence and connectedness of solution sets of vector variational inequalities. Mathematical Methods of Operations Research 2001, 54(2):201–215. 10.1007/s001860100147
Ahmad R, Khan Z: Vector variational-like inequalities with -generally convex mappings. The Australian & New Zealand Industrial and Applied Mathematics Journal 2007, 49: E33-E46.
Fang Y-P, Huang N-J: Strong vector variational inequalities in Banach spaces. Applied Mathematics Letters 2006, 19(4):362–368. 10.1016/j.aml.2005.06.008
Chen G-Y, Hou S-H: Existence of solutions for vector variational inequalities. In Vector Variational Inequalities and Vector Equilibria. Volume 38. Edited by: Gisannessi F. Kluwer Acadiemic Publishers, Dordrecht, The Netherlands; 2000:73–86. 10.1007/978-1-4613-0299-5_5
Lee BS, Khan MF, Salahuddin : Generalized vector variational-type inequalities. Computers & Mathematics with Applications 2008, 55(6):1164–1169. 10.1016/j.camwa.2007.04.045
Chen GY: Existence of solutions for a vector variational inequality: an extension of the Hartmann-Stampacchia theorem. Journal of Optimization Theory and Applications 1992, 74(3):445–456. 10.1007/BF00940320
Fan K: Some properties of convex sets related to fixed point theorems. Mathematische Annalen 1984, 266(4):519–537. 10.1007/BF01458545
Taylor AE: An Introduction to Functional Analysis. John Wiley & Sons, New York, NY, USA; 1963.
Aubin J-P, Ekeland I: Applied Nonlinear Analysis, Pure and Applied Mathematics. Wiley-Interscience, New York, NY, USA; 1984:xi+518.
Ahmad MK, Salahuddin : Existence of solutions for generalized implicit vector variational-like inequalities. Nonlinear Analysis: Theory, Methods & Applications 2007, 67(2):430–441. 10.1016/j.na.2006.06.010
Jabarootian T, Zafarani J: Generalized vector variational-like inequalities. Journal of Optimization Theory and Applications 2008, 136(1):15–30. 10.1007/s10957-007-9300-3
Acknowledgments
The authors greatly appreciate the editor and the anonymous referees for their useful comments and suggestions. This work was supported by the Key Program of NSFC (Grant no. 70831005), the Kyungnam University Research Fund 2009, and the Open Fund (PLN0904) of State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation (Southwest Petroleum University).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, X., Kim, J. & Huang, NJ. Existence of Solutions for 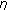 -Generalized Vector Variational-Like Inequalities.
J Inequal Appl 2010, 968271 (2010). https://doi.org/10.1155/2010/968271
-Generalized Vector Variational-Like Inequalities.
J Inequal Appl 2010, 968271 (2010). https://doi.org/10.1155/2010/968271
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/968271
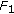 is a KKM mapping. Indeed, assume that
is a KKM mapping. Indeed, assume that 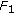 is not a KKM mapping; then there exist
is not a KKM mapping; then there exist 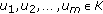 ,
, 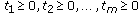 with
with 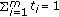 and
and  such that
such that