- Research Article
- Open access
- Published:
Some Iterative Methods for Solving Equilibrium Problems and Optimization Problems
Journal of Inequalities and Applications volume 2010, Article number: 943275 (2010)
Abstract
We introduce a new iterative scheme for finding a common element of the set of solutions of the equilibrium problems, the set of solutions of variational inequality for a relaxed cocoercive mapping, and the set of fixed points of a nonexpansive mapping. The results presented in this paper extend and improve some recent results of Ceng and Yao (2008), Yao (2007), S. Takahashi and W. Takahashi (2007), Marino and Xu (2006), Iiduka and Takahashi (2005), Su et al. (2008), and many others.
1. Introduction
Throughout this paper, we always assume that  is a real Hilbert space with inner product
is a real Hilbert space with inner product  and norm
and norm  , respectively,
, respectively,  is a nonempty closed and convex subset of
is a nonempty closed and convex subset of  , and
, and  is the metric projection of
is the metric projection of  onto
onto  . In the following, we denote by "
. In the following, we denote by " '' strong convergence, by "
'' strong convergence, by " '' weak convergence, and by "
'' weak convergence, and by " '' the real number set. Recall that a mapping
'' the real number set. Recall that a mapping  is called nonexpansive if
is called nonexpansive if

We denote by  the set of fixed points of the mapping
the set of fixed points of the mapping  .
.
For a given nonlinear operator  , consider the problem of finding
, consider the problem of finding  such that
such that

which is called the variational inequality. For the recent applications, sensitivity analysis, dynamical systems, numerical methods, and physical formulations of the variational inequalities, see [1–24] and the references therein.
For a given  ,
,  satisfies the inequality
satisfies the inequality

if and only if  , where
, where  is the projection of the Hilbert space onto the closed convex set
is the projection of the Hilbert space onto the closed convex set  .
.
It is known that projection operator  is nonexpansive. It is also known that
is nonexpansive. It is also known that  satisfies
satisfies

Moreover,  is characterized by the properties
is characterized by the properties  and
and  for all
for all  .
.
Using characterization of the projection operator, one can easily show that the variational inequality (1.2) is equivalent to finding the fixed point problem of finding  which satisfies the relation
which satisfies the relation

where  is a constant.
is a constant.
This fixed-point formulation has been used to suggest the following iterative scheme. For a given  ,
,

which is known as the projection iterative method for solving the variational inequality (1.2). The convergence of this iterative method requires that the operator  must be strongly monotone and Lipschitz continuous. These strict conditions rule out their applications in many important problems arising in the physical and engineering sciences. To overcome these drawbacks, Noor [2, 3] used the technique of updating the solution to suggest the two-step (or predictor-corrector) method for solving the variational inequality (1.2). For a given
must be strongly monotone and Lipschitz continuous. These strict conditions rule out their applications in many important problems arising in the physical and engineering sciences. To overcome these drawbacks, Noor [2, 3] used the technique of updating the solution to suggest the two-step (or predictor-corrector) method for solving the variational inequality (1.2). For a given  ,
,

which is also known as the modified double-projection method. For the convergence analysis and applications of this method, see the works of Noor [3] and Y. Yao and J.-C. Yao [16].
Numerous problems in physics, optimization, and economics reduce to find a solution of (2.12). Some methods have been proposed to solve the equilibrium problem; see [4, 5]. Combettes and Hirstoaga [4] introduced an iterative scheme for finding the best approximation to the initial data when  is nonempty and proved a strong convergence theorem. Very recently, S. Takahashi and W. Takahashi [6] also introduced a new iterative scheme,
is nonempty and proved a strong convergence theorem. Very recently, S. Takahashi and W. Takahashi [6] also introduced a new iterative scheme,

for approximating a common element of the set of fixed points of a nonexpansive nonself mapping and the set of solutions of the equilibrium problem and obtained a strong convergence theorem in a real Hilbert space.
Iterative methods for nonexpansive mappings have recently been applied to solve convex minimization problems; see [7–11] and the references therein. A typical problem is to minimize a quadratic function over the set of the fixed points of a nonexpansive mapping on a real Hilbert space  :
:

where  is a linear bounded operator,
is a linear bounded operator,  is the fixed point set of a nonexpansive mapping
is the fixed point set of a nonexpansive mapping  , and
, and  is a given point in
is a given point in  . In [10, 11], it is proved that the sequence
. In [10, 11], it is proved that the sequence  defined by the iterative method below, with the initial guess
defined by the iterative method below, with the initial guess  chosen arbitrarily,
chosen arbitrarily,

converges strongly to the unique solution of the minimization problem (1.9) provided the sequence  satisfies certain conditions. Recently, Marino and Xu [8] introduced a new iterative scheme by the viscosity approximation method [12]:
satisfies certain conditions. Recently, Marino and Xu [8] introduced a new iterative scheme by the viscosity approximation method [12]:

They proved that the sequence  generated by the above iterative scheme converges strongly to the unique solution of the variational inequality
generated by the above iterative scheme converges strongly to the unique solution of the variational inequality

which is the optimality condition for the minimization problem

where  is the fixed point set of a nonexpansive mapping
is the fixed point set of a nonexpansive mapping  and
and  a potential function for
a potential function for  (i.e.,
(i.e.,  for
for  ).
).
For finding a common element of the set of fixed points of nonexpansive mappings and the set of solution of variational inequalities for α-cocoercive map, Takahashi and Toyoda [13] introduced the following iterative process:

for every  , where
, where  is α-cocoercive,
is α-cocoercive,  ,
,  is a sequence in (0,1), and
is a sequence in (0,1), and  is a sequence in
is a sequence in  . They showed that, if
. They showed that, if  is nonempty, then the sequence
is nonempty, then the sequence  generated by (1.14) converges weakly to some
generated by (1.14) converges weakly to some  . Recently, Iiduka and Takahashi [14] proposed another iterative scheme as follows:
. Recently, Iiduka and Takahashi [14] proposed another iterative scheme as follows:

for every  , where
, where  is α-cocoercive,
is α-cocoercive,  ,
,  is a sequence in (0,1), and
is a sequence in (0,1), and  is a sequence in
is a sequence in  . They proved that the sequence
. They proved that the sequence  converges strongly to
converges strongly to  .
.
Recently, Chen et al. [15] studied the following iterative process:

and also obtained a strong convergence theorem by viscosity approximation method.
Inspired and motivated by the ideas and techniques of Noor [2, 3] and Y. Yao and J.-C. Yao [16] introduce the following iterative scheme.
Let  be a closed convex subset of real Hilbert space
be a closed convex subset of real Hilbert space  . Let
. Let  be an α-inverse strongly monotone mapping of
be an α-inverse strongly monotone mapping of  into
into  , and let
, and let  be a nonexpansive mapping of
be a nonexpansive mapping of  into itself such that
into itself such that  . Suppose that
. Suppose that  and
and  ,
,  are given by
are given by

where  ,
,  , and
, and  are the sequences in
are the sequences in  and
and  is a sequence in
is a sequence in  . They proved that the sequence
. They proved that the sequence  defined by (1.17) converges strongly to common element of the set of fixed points of a nonexpansive mapping and the set of solutions of the variational inequality for α-inverse-strongly monotone mappings under some parameters controlling conditions.
defined by (1.17) converges strongly to common element of the set of fixed points of a nonexpansive mapping and the set of solutions of the variational inequality for α-inverse-strongly monotone mappings under some parameters controlling conditions.
In this paper motivated by the iterative schemes considered in [6, 15, 16], we introduce a general iterative process as follows:

where  is a linear bounded operator and
is a linear bounded operator and  is relaxed cocoercive. We prove that the sequence
is relaxed cocoercive. We prove that the sequence  generated by the above iterative scheme converges strongly to a common element of the set of fixed points of a nonexpansive mapping, the set of solutions of the variational inequalities for a relaxed cocoercive mapping, and the set of solutions of the equilibrium problems (2.12), which solves another variational inequality
generated by the above iterative scheme converges strongly to a common element of the set of fixed points of a nonexpansive mapping, the set of solutions of the variational inequalities for a relaxed cocoercive mapping, and the set of solutions of the equilibrium problems (2.12), which solves another variational inequality

where  and is also the optimality condition for the minimization problem
and is also the optimality condition for the minimization problem  , where
, where  is a potential function for
is a potential function for  (i.e.,
(i.e.,  for
for  ). The results obtained in this paper improve and extend the recent ones announced by S. Takahashi and W. Takahashi [6], Iiduka and Takahashi [14], Marino and Xu [8], Chen et al. [15], Y. Yao and J.-C. Yao [16], Ceng and Yao [22], Su et al. [17], and many others.
). The results obtained in this paper improve and extend the recent ones announced by S. Takahashi and W. Takahashi [6], Iiduka and Takahashi [14], Marino and Xu [8], Chen et al. [15], Y. Yao and J.-C. Yao [16], Ceng and Yao [22], Su et al. [17], and many others.
2. Preliminaries
For solving the equilibrium problem for a bifunction  , let us assume that
, let us assume that  satisfies the following conditions:
satisfies the following conditions:
(A1) for all
for all  ;
;
(A2) is monotone, that is,
is monotone, that is,  for all
for all  ;
;
(A3) for each  ,
,  ;
;
(A4) for each  ,
,  is convex and lower semicontinuous.
is convex and lower semicontinuous.
Recall the following.
-
(1)
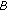
is called
 -strong monotone if for all
-strong monotone if for all 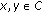 , we have
, we have 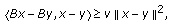 (2.1)
(2.1)
for a constant  . This implies that
. This implies that

that is,  is
is  -expansive, and when
-expansive, and when  , it is expansive.
, it is expansive.
Clearly, every  -cocoercive map
-cocoercive map  is
is  -Lipschitz continuous.
-Lipschitz continuous.
-
(3)
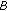
is called
 -cocoercive if there exists a constant
-cocoercive if there exists a constant 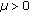 such that
such that  (2.4)
(2.4)
-
(4)

is said to be relaxed
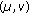 -cocoercive if there exists two constants
-cocoercive if there exists two constants 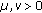 such that
such that 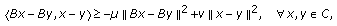 (2.5)
(2.5)
for  ,
,  is
is  -strongly monotone. This class of maps are more general than the class of strongly monotone maps. It is easy to see that we have the following implication:
-strongly monotone. This class of maps are more general than the class of strongly monotone maps. It is easy to see that we have the following implication:  -strongly monotonicity
-strongly monotonicity  relaxed
relaxed  -cocoercivity.
-cocoercivity.
We will give the practical example of the relaxed  -cocoercivity and Lipschitz continuous operator.
-cocoercivity and Lipschitz continuous operator.
Example 2.1.
Let  , for all
, for all  , for a constant
, for a constant  ; then,
; then,  is relaxed
is relaxed  -cocoercive and Lipschitz continuous. Especially,
-cocoercive and Lipschitz continuous. Especially,  is
is  -strong monotone.
-strong monotone.
Proof.
-
1.
Since
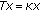 , for all
, for all 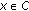 , we have
, we have 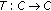 . For for all
. For for all 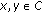 , for all
, for all 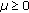 , we also have the below
, we also have the below 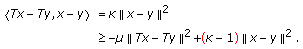 (2.6)
(2.6)
Taking  , it is clear that
, it is clear that  is relaxed
is relaxed  -cocoercive.
-cocoercive.
-
2.
Obviously, for for all
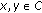
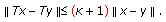 (2.7)
(2.7)
Then,  is
is  Lipschitz continuous.
Lipschitz continuous.
Especially, Taking  , we observe that
, we observe that

Obviously,  is
is  -strong monotone.
-strong monotone.
The proof is completed.
-
(5)
A mapping
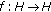 is said to be a contraction if there exists a coefficient
is said to be a contraction if there exists a coefficient 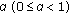 such that
such that 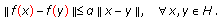 (2.9)
(2.9)
-
(6)
An operator
 is strong positive if there exists a constant
is strong positive if there exists a constant 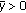 with the property
with the property  (2.10)
(2.10)
-
(7)
A set-valued mapping
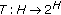 is called monotone if for all
is called monotone if for all  ,
,  , and
, and 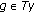 imply
imply 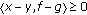 . A monotone mapping
. A monotone mapping  is maximal if the graph of
is maximal if the graph of 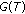 of
of 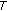 is not properly contained in the graph of any other monotone mapping. It is well known that a monotone mapping
is not properly contained in the graph of any other monotone mapping. It is well known that a monotone mapping 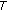 is maximal if and only if for
is maximal if and only if for 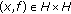 ,
,  for every
for every 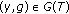 implies
implies 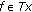 .
.
Let  be a monotone map of
be a monotone map of  into
into  and let
and let  be the normal cone to
be the normal cone to  at
at  , that is,
, that is,  and define
and define

Then  is the maximal monotone and
is the maximal monotone and  if and only if
if and only if  ; see [1].
; see [1].
Related to the variational inequality problem (1.2), we consider the equilibrium problem, which was introduced by Blum and Oettli [19] and Noor and Oettli [20] in 1994. To be more precise, let  be a bifunction of
be a bifunction of  into
into  , where
, where  is the set of real numbers.
is the set of real numbers.
For given bifunction  , we consider the problem of finding
, we consider the problem of finding  such that
such that

which is known as the equilibrium problem. The set of solutions of (2.12) is denoted by  . Given a mapping
. Given a mapping  , let
, let  for all
for all  . Then
. Then  if and only if
if and only if  for all
for all  , that is,
, that is,  is a solution of the variational inequality. That is to say, the variational inequality problem is included by equilibrium problem, and the variational inequality problem is the special case of equilibrium problem.
is a solution of the variational inequality. That is to say, the variational inequality problem is included by equilibrium problem, and the variational inequality problem is the special case of equilibrium problem.
Assume that  is a potential function for
is a potential function for  (i.e.,
(i.e.,  for all
for all  ), it is well known that
), it is well known that  satisfies the optimality condition
satisfies the optimality condition  for all
for all  if and only if
if and only if

We can rewrite the variational inequality  for all
for all  as, for any
as, for any  ,
,

If we introduce the nearest point projection  from
from  onto
onto  ,
,

which is characterized by the inequality

then we see from the above (2.14) that the minimization (2.13) is equivalent to the fixed point problem

Therefore, they have a relation as follows:

In addition to this, based on the result (3) of Lemma 2.7,  , we know if the element
, we know if the element  , we have
, we have  is the solution of the nonlinear equation
is the solution of the nonlinear equation

where  is defined as in Lemma 2.7. Once we have the solutions of the equation (2.19), then it simultaneously solves the fixed points problems, equilibrium points problems, and variational inequalities problems. Therefore, the constrained set
is defined as in Lemma 2.7. Once we have the solutions of the equation (2.19), then it simultaneously solves the fixed points problems, equilibrium points problems, and variational inequalities problems. Therefore, the constrained set  is very important and applicable.
is very important and applicable.
We now recall some well-known concepts and results. It is well-known that for all  and
and  there holds
there holds

A space  is said to satisfy Opial's condition [18] if for each sequence
is said to satisfy Opial's condition [18] if for each sequence  in
in  which converges weakly to point
which converges weakly to point  , we have
, we have

Assume that  is a sequence of nonnegative real numbers such that
is a sequence of nonnegative real numbers such that

where  is a sequence in (0,1) and
is a sequence in (0,1) and  is a sequence such that
is a sequence such that
(i) ;
;
(ii) or
or  .
.
Then  .
.
Lemma 2.3.
In a real Hilbert space  , the following inequality holds:
, the following inequality holds:

Lemma 2.4 (Marino and Xu [8]).
Assume that  is a strong positive linear bounded operator on a Hilbert space
is a strong positive linear bounded operator on a Hilbert space  with coefficient
with coefficient  and
and  . Then
. Then  .
.
Lemma 2.5 (see [21]).
Let  and
and  be bounded sequences in a Banach space
be bounded sequences in a Banach space  and let
and let  be a sequence in
be a sequence in  with
with  . Suppose
. Suppose  for all integers
for all integers  and
and  . Then,
. Then,  .
.
Lemma 2.6 (Blum and Oettli [19]).
Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  and let
and let  be a bifunction of
be a bifunction of  into
into  satisfying (A1)–(A4). Let
satisfying (A1)–(A4). Let  and
and  . Then, there exists
. Then, there exists  such that
such that

Lemma 2.7 (Combettes and Hirstoaga [4]).
Assume that  satisfies (A1)–(A4). For
satisfies (A1)–(A4). For  and
and  , define a mapping
, define a mapping  as follows:
as follows:

for all  . Then, the following hold:
. Then, the following hold:
(1) is single-valued;
is single-valued;
(2) is firmly nonexpansive, that is, for any
is firmly nonexpansive, that is, for any  ,
,  ;
;
(3) ;
;
(4) is closed and convex.
is closed and convex.
3. Main Results
Theorem 3.1.
Let  be a nonempty closed convex subset of a Hilbert space
be a nonempty closed convex subset of a Hilbert space  . Let
. Let  be a bifunction of
be a bifunction of  into
into  which satisfies (A1)–(A4), let
which satisfies (A1)–(A4), let  be a nonexpansive mapping of
be a nonexpansive mapping of  into
into  , and let
, and let  be a
be a  -Lipschitzian, relaxed
-Lipschitzian, relaxed  -cocoercive map of
-cocoercive map of  into
into  such that
such that  . Let
. Let  be a strongly positive linear bounded operator with coefficient
be a strongly positive linear bounded operator with coefficient  . Assume that
. Assume that  . Let
. Let  be a contraction of
be a contraction of  into itself with a coefficient
into itself with a coefficient  and let
and let  and
and  be sequences generated by
be sequences generated by  and
and

for all  , where
, where  and
and  satisfy
satisfy
(C1) ;
;
(C2) ;
;
(C3) ;
;
(C4) ,
,  and
and  ;
;
(C5) ;
;
(C6) for some
for some  ,
,  with
with  .
.
Then, both  and
and  converge strongly to
converge strongly to  , where
, where  , which solves the following variational inequality:
, which solves the following variational inequality:

Proof.
Note that from the condition (C1), we may assume, without loss of generality, that  . Since
. Since  is a strongly positive bounded linear operator on
is a strongly positive bounded linear operator on  , then
, then

observe that

that is to say  is positive. It follows that
is positive. It follows that

First, we show that  is nonexpansive. Indeed, from the relaxed
is nonexpansive. Indeed, from the relaxed  -cocoercive and
-cocoercive and  -Lipschitzian definition on
-Lipschitzian definition on  and condition (C6), we have
and condition (C6), we have

which implies that the mapping  is nonexpansive.
is nonexpansive.
Now, we observe that  is bounded. Indeed, take
is bounded. Indeed, take  , since
, since  , we have
, we have

Put  , since
, since  , we have
, we have  . Therefore, we have
. Therefore, we have

Due to (3.5), it follows that

It follows from (3.9) that

Hence,  is bounded, so are
is bounded, so are  ,
,  , and
, and  .
.
Next, we show that

Observing that  and
and  , we have
, we have


Putting  in (3.12) and
in (3.12) and  in (3.13), we have
in (3.13), we have

It follows from (A2) that

That is,

Without loss of generality, let us assume that there exists a real number  such that
such that  for all
for all  . It follows that
. It follows that

It follows that

where  is an appropriate constant such that
is an appropriate constant such that  . Note that
. Note that

Substituting (3.18) into (3.19) yields that

where  is an appropriate constant such that
is an appropriate constant such that  .
.
Define

Observe that from the definition of  , we obtain
, we obtain

It follows that with

This together with (C1), (C3), and (C4) implies that

Hence, by Lemma 2.5, we obtain  as
as  .
.
Consequently,

Note that

This together with (3.25) implies that

For  , we have
, we have

and hence

Set  as a constant such that
as a constant such that

By (3.29) and (3.30), we have

It follows that

By  and
and  , as
, as  , and
, and  is bounded, we obtain that
is bounded, we obtain that

For  , we have
, we have

Observe (3.31) that

Substituting (3.34) into (3.35), we have

It follows from condition (C6) that

From condition (C1) and (3.25), we have that

On the other hand, we have

which yields that

Substituting (3.40) into (3.35) yields that

It follows that

From condition (C1), (3.25), and (3.38), we have that

Observe that

From (3.27), (3.33), and (3.43), we have

Observe that  is a contraction. Indeed, for all
is a contraction. Indeed, for all  , we have
, we have

Banach's Contraction Mapping Principle guarantees that  has a unique fixed point, say
has a unique fixed point, say  , that is,
, that is,  .
.
Next, we show that

To see this, we choose a subsequence  of
of  such that
such that

Correspondingly, there exists a subsequence  of
of  . Since
. Since  is bounded, there exists a subsequence
is bounded, there exists a subsequence  of
of  which converges weakly to
which converges weakly to  . Without loss of generality, we can assume that
. Without loss of generality, we can assume that  .
.
Next, we show that  . First, we prove
. First, we prove  . Since
. Since  , we have
, we have

It follows from (A2) that,

It follows that

Since  ,
,  , and (A4), we have
, and (A4), we have  for all
for all  . For
. For  with
with  and
and  , let
, let  . Since
. Since  and
and  , we have
, we have  and hence
and hence  . So, from (A1) and (A4), we have
. So, from (A1) and (A4), we have

That is,  . It follows from (A3) that
. It follows from (A3) that  for all
for all  and hence
and hence  . Since Hilbert spaces satisfy Opial's condition, from (3.43), suppose
. Since Hilbert spaces satisfy Opial's condition, from (3.43), suppose  ; we have
; we have

which is a contradiction. Thus, we have  .
.
Next, let us show that  . Put
. Put

Since  is relaxed
is relaxed  -cocoercive and from condition (C6), we have
-cocoercive and from condition (C6), we have

which yields that  is monotone. Thus
is monotone. Thus  is maximal monotone. Let
is maximal monotone. Let  . Since
. Since  and
and  , we have
, we have

On the other hand, from  , we have
, we have

and hence

It follows that

which implies that  , We have
, We have  and hence
and hence  . That is,
. That is,  .
.
Since  , we have
, we have

That is, (3.47) holds.
Finally, we show that  , where
, where  , which solves the following variational inequality:
, which solves the following variational inequality:

We consider

which implies that

Since  ,
,  , and
, and  are bounded, we can take a constant
are bounded, we can take a constant  such that
such that

for all  . It then follows that
. It then follows that

where

From (3.27) and (3.47), we also have

By (C1), (3.47), and (3.67), we get  . Now applying Lemma 2.2 to (3.65) concludes that
. Now applying Lemma 2.2 to (3.65) concludes that  .
.
This completes the proof.
Remark 3.2.
Some iterative algorithms were presented in Yamada [11], Combettes [24], and Iiduka-Yamada [25], for example, the steepest descent method, the hybrid steepest descent method, and the conjugate gradient methods; these methods have common form

where  is the
is the  th approximation to the solution,
th approximation to the solution,  is a step size, and
is a step size, and  is a search direction. In this paper, We define
is a search direction. In this paper, We define  ; the method (3.1) will be changed as
; the method (3.1) will be changed as

Take  , the method (3.1) will be changed as (3.68).
, the method (3.1) will be changed as (3.68).
Remark 3.3.
The computational possibility of the resolvent,  , of
, of  in Lemma 2.7 and Theorem 3.1 is well defined mathematically, but, in general, the computation of
in Lemma 2.7 and Theorem 3.1 is well defined mathematically, but, in general, the computation of  is very difficult in large-scale finite spaces and infinite spaces.
is very difficult in large-scale finite spaces and infinite spaces.
4. Applications
Theorem 4.1.
Let  be a nonempty closed convex subset of a Hilbert space
be a nonempty closed convex subset of a Hilbert space  . Let
. Let  be a bifunction of
be a bifunction of  into
into  which satisfies (A1)–(A4); let
which satisfies (A1)–(A4); let  be a nonexpansive mapping of
be a nonexpansive mapping of  into
into  such that
such that  . Let
. Let  be a strongly positive linear bounded operator with coefficient
be a strongly positive linear bounded operator with coefficient  . Assume that
. Assume that  . Let
. Let  be a contraction of
be a contraction of  into itself with a coefficient
into itself with a coefficient  and let
and let  and
and  be sequences generated by
be sequences generated by  and
and

for all  , where
, where  and
and  satisfy
satisfy
(C1) ;
;
(C2) ;
;
(C3) ;
;
(C4) and
and  ;
;
(C5) .
.
Then, both  and
and  converge strongly to
converge strongly to  , where
, where  , which solves the following variational inequality:
, which solves the following variational inequality:

Proof.
Taking  in Theorem 3.1, we can get the desired conclusion easily.
in Theorem 3.1, we can get the desired conclusion easily.
Theorem 4.2.
Let  be a nonempty closed convex subset of a Hilbert space
be a nonempty closed convex subset of a Hilbert space  , let
, let  be a nonexpansive mapping of
be a nonexpansive mapping of  into
into  , and let
, and let  be a
be a  -Lipschitzian, relaxed
-Lipschitzian, relaxed  -cocoercive map of
-cocoercive map of  into
into  such that
such that  . Let
. Let  be a strongly positive linear bounded operator with coefficient
be a strongly positive linear bounded operator with coefficient  . Assume that
. Assume that  . Let
. Let  be a contraction of
be a contraction of  into itself with a coefficient
into itself with a coefficient  and let
and let  and
and  be sequences generated by
be sequences generated by  and
and

for all  , where
, where  and
and  satisfy
satisfy
(C1) ;
;
(C2) ;
;
(C3) ;
;
(C4) and
and  ;
;
(C5) ;
;
(C6) for some
for some  ,
,  with
with  .
.
Then, both  and
and  converge strongly to
converge strongly to  , where
, where  , which solves the following variational inequality:
, which solves the following variational inequality:

Proof.
Put  for all
for all  and
and  for all
for all  in Theorem 3.1. Then we have
in Theorem 3.1. Then we have  . we can obtain the desired conclusion easily.
. we can obtain the desired conclusion easily.
References
Rockafellar RT: On the maximality of sums of nonlinear monotone operators. Transactions of the American Mathematical Society 1970, 149: 75–88. 10.1090/S0002-9947-1970-0282272-5
Noor MA: New approximation schemes for general variational inequalities. Journal of Mathematical Analysis and Applications 2000, 251(1):217–229. 10.1006/jmaa.2000.7042
Noor MA: Some developments in general variational inequalities. Applied Mathematics and Computation 2004, 152(1):199–277. 10.1016/S0096-3003(03)00558-7
Combettes PL, Hirstoaga SA: Equilibrium programming in Hilbert spaces. Journal of Nonlinear and Convex Analysis 2005, 6(1):117–136.
Flåm SD, Antipin AS: Equilibrium programming using proximal-like algorithms. Mathematical Programming 1997, 78(1):29–41.
Takahashi S, Takahashi W: Viscosity approximation methods for equilibrium problems and fixed point problems in Hilbert spaces. Journal of Mathematical Analysis and Applications 2007, 331(1):506–515. 10.1016/j.jmaa.2006.08.036
Deutsch F, Yamada I: Minimizing certain convex functions over the intersection of the fixed point sets of nonexpansive mappings. Numerical Functional Analysis and Optimization 1998, 19(1–2):33–56.
Marino G, Xu H-K: A general iterative method for nonexpansive mappings in Hilbert spaces. Journal of Mathematical Analysis and Applications 2006, 318(1):43–52. 10.1016/j.jmaa.2005.05.028
Xu H-K: Iterative algorithms for nonlinear operators. Journal of the London Mathematical Society 2002, 66(1):240–256. 10.1112/S0024610702003332
Xu HK: An iterative approach to quadratic optimization. Journal of Optimization Theory and Applications 2003, 116(3):659–678. 10.1023/A:1023073621589
Yamada I: The hybrid steepest descent method for the variational inequality problem over the intersection of fixed point sets of nonexpansive mappings. In Inherently Parallel Algorithms in Feasibility and Optimization and Their Applications (Haifa, 2000), Studies in Computational Mathematics. Volume 8. Edited by: Butnariu D, Censor Y, Reich S. North-Holland, Amsterdam, The Netherlands; 2001:473–504.
Moudafi A: Viscosity approximation methods for fixed-points problems. Journal of Mathematical Analysis and Applications 2000, 241(1):46–55. 10.1006/jmaa.1999.6615
Takahashi W, Toyoda M: Weak convergence theorems for nonexpansive mappings and monotone mappings. Journal of Optimization Theory and Applications 2003, 118(2):417–428. 10.1023/A:1025407607560
Iiduka H, Takahashi W: Strong convergence theorems for nonexpansive mappings and inverse-strongly monotone mappings. Nonlinear Analysis: Theory, Methods & Applications 2005, 61(3):341–350. 10.1016/j.na.2003.07.023
Chen J, Zhang L, Fan T: Viscosity approximation methods for nonexpansive mappings and monotone mappings. Journal of Mathematical Analysis and Applications 2007, 334(2):1450–1461. 10.1016/j.jmaa.2006.12.088
Yao Y, Yao J-C: On modified iterative method for nonexpansive mappings and monotone mappings. Applied Mathematics and Computation 2007, 186(2):1551–1558. 10.1016/j.amc.2006.08.062
Su Y, Shang M, Qin X: An iterative method of solution for equilibrium and optimization problems. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(8):2709–2719. 10.1016/j.na.2007.08.045
Opial Z: Weak convergence of the sequence of successive approximations for nonexpansive mappings. Bulletin of the American Mathematical Society 1967, 73: 591–597. 10.1090/S0002-9904-1967-11761-0
Blum E, Oettli W: From optimization and variational inequalities to equilibrium problems. The Mathematics Student 1994, 63(1–4):123–145.
Noor MA, Oettli W: On general nonlinear complementarity problems and quasi-equilibria. Le Matematiche 1994, 49(2):313–331.
Suzuki T: Strong convergence of Krasnoselskii and Mann's type sequences for one-parameter nonexpansive semigroups without Bochner integrals. Journal of Mathematical Analysis and Applications 2005, 305(1):227–239. 10.1016/j.jmaa.2004.11.017
Ceng L-C, Yao J-C: Hybrid viscosity approximation schemes for equilibrium problems and fixed point problems of infinitely many nonexpansive mappings. Applied Mathematics and Computation 2008, 198(2):729–741. 10.1016/j.amc.2007.09.011
Noor MA, Noor KI, Yaqoob H: On general mixed variational inequalities. Acta Applicandae Mathematicae 2010, 110(1):227–246. 10.1007/s10440-008-9402-4
Combettes PL: A block-iterative surrogate constraint splitting method for quadratic signal recovery. IEEE Transactions on Signal Processing 2003, 51(7):1771–1782. 10.1109/TSP.2003.812846
Iiduka H, Yamada I: A use of conjugate gradient direction for the convex optimization problem over the fixed point set of a nonexpansive mapping. SIAM Journal on Optimization 2008, 19(4):1881–1893.
Acknowledgments
This work is supported by the Fundamental Research Funds for the Central Universities, no. JY10000970006 and National Science Foundation of China, no. 60974082.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
He, H., Liu, S. & Fan, Q. Some Iterative Methods for Solving Equilibrium Problems and Optimization Problems. J Inequal Appl 2010, 943275 (2010). https://doi.org/10.1155/2010/943275
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/943275
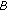
 -strong monotone if for all
-strong monotone if for all 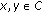 , we have
, we have 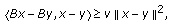

 -cocoercive [
-cocoercive [ , we have
, we have 
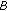
 -cocoercive if there exists a constant
-cocoercive if there exists a constant 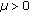 such that
such that 

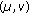 -cocoercive if there exists two constants
-cocoercive if there exists two constants 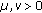 such that
such that 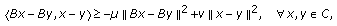
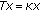 , for all
, for all 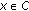 , we have
, we have 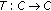 . For for all
. For for all 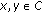 , for all
, for all 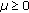 , we also have the below
, we also have the below 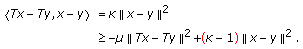
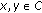
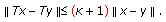
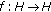 is said to be a contraction if there exists a coefficient
is said to be a contraction if there exists a coefficient 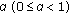 such that
such that 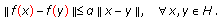
 is strong positive if there exists a constant
is strong positive if there exists a constant 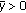 with the property
with the property 
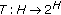 is called monotone if for all
is called monotone if for all  ,
,  , and
, and 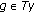 imply
imply 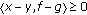 . A monotone mapping
. A monotone mapping  is maximal if the graph of
is maximal if the graph of 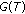 of
of 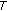 is not properly contained in the graph of any other monotone mapping. It is well known that a monotone mapping
is not properly contained in the graph of any other monotone mapping. It is well known that a monotone mapping 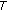 is maximal if and only if for
is maximal if and only if for 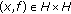 ,
,  for every
for every 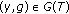 implies
implies 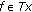 .
.