- Research Article
- Open access
- Published:
An Algorithm for Finding a Common Solution for a System of Mixed Equilibrium Problem, Quasivariational Inclusion Problem, and Fixed Point Problem of Nonexpansive Semigroup
Journal of Inequalities and Applications volume 2010, Article number: 895907 (2010)
Abstract
We introduce a hybrid iterative scheme for finding a common element of the set of solutions for a system of mixed equilibrium problems, the set of common fixed point for nonexpansive semigroup, and the set of solutions of the quasi-variational inclusion problem with multivalued maximal monotone mappings and inverse-strongly monotone mappings in Hilbert space. Under suitable conditions, some strong convergence theorems are proved. Our results extend some recent results announced by some authors.
1. Introduction
Throughout this paper we assume that  is a real Hilbert space, and
is a real Hilbert space, and  is a nonempty closed convex subset of
is a nonempty closed convex subset of  .
.
In the sequel, we denote the set of fixed points of  by
by  .
.
A bounded linear operator  is said to be strongly positive, if there exists a constant
is said to be strongly positive, if there exists a constant  such that
such that

Let  be a single-valued nonlinear mapping and
be a single-valued nonlinear mapping and  a multivalued mapping. The "so-called" quasi-variational inclusion problem (see, Chang [1, 2]) is to find an
a multivalued mapping. The "so-called" quasi-variational inclusion problem (see, Chang [1, 2]) is to find an  such that
such that

A number of problems arising in structural analysis, mechanics, and economics can be studied in the framework of this kind of variational inclusions (see, e.g., [3]).
The set of solutions of variational inclusion (1.2) is denoted by  .
.
Special Case
If  , where
, where  is a nonempty closed convex subset of
is a nonempty closed convex subset of  , and
, and  is the indicator function of
is the indicator function of  , that is,
, that is,

then the variational inclusion problem (1.2) is equivalent to find  such that
such that

This problem is called Hartman-Stampacchia variational inequality problem (see, e.g., [4]). The set of solutions of (1.4) is denoted by  .
.
Recall that a mapping  is called
is called  -inverse strongly monotone (see [5]), if there exists an
-inverse strongly monotone (see [5]), if there exists an  such that
such that

A multivalued mapping  is called monotone, if for all
is called monotone, if for all  ,
,  , and
, and  , then it implies that
, then it implies that  . A multivalued mapping
. A multivalued mapping  is called maximal monotone, if it is monotone and if for any
is called maximal monotone, if it is monotone and if for any 

(the graph of mapping  ) implies that
) implies that  .
.
Proposition 1.1 (see [5]).
Let  be an
be an  -inverse strongly monotone mapping, then
-inverse strongly monotone mapping, then
(a) is a
is a  -Lipschitz continuous and monotone mapping;
-Lipschitz continuous and monotone mapping;
(b)if  is any constant in
is any constant in  , then the mapping
, then the mapping  is nonexpansive, where
is nonexpansive, where  is the identity mapping on
is the identity mapping on  .
.
Let  be an equilibrium bifunction (i.e.,
be an equilibrium bifunction (i.e.,  ), and let
), and let  be a real-valued function.
be a real-valued function.
Recently, Ceng and Yao [6] introduced the following mixed equilibrium problem , that is, to find
, that is, to find  such that
such that

The set of solutions of (1.7) is denoted by  , that is,
, that is,

In particular, if  , this problem reduces to the equilibrium problem, that is, to find
, this problem reduces to the equilibrium problem, that is, to find  such that
such that

Denote the set of solution of EP by  .
.
On the other hand, Li et al. [7] introduced two steps of iterative procedures for the approximation of common fixed point of a nonexpansive semigroup  on a nonempty closed convex subset
on a nonempty closed convex subset  in a Hilbert space.
in a Hilbert space.
Very recently, Saeidi [8] introduced a more general iterative algorithm for finding a common element of the set of solutions for a system of equilibrium problems and of the set of common fixed points for a finite family of nonexpansive mappings and a nonexpansive semigroup.
Recall that a family of mappings  is called a nonexpansive semigroup, if it satisfies the following conditions:
is called a nonexpansive semigroup, if it satisfies the following conditions:
(a) for all
for all  and
and  ;
;
(b) .
.
(c)the mapping  is continuous, for each
is continuous, for each  .
.
Motivated and inspired by Ceng and Yao [6], Li et al. [7], Saeidi [8], and [9–13], the purpose of this paper is to introduce a hybrid iterative scheme for finding a common element of the set of solutions for a system of mixed equilibrium problems, the set of common fixed point for a nonexpansive semigroup, and the set of solutions of the quasi-variational inclusion problem with multivalued maximal monotone mappings and inverse-strongly monotone mappings in Hilbert space. Under suitable conditions, some strong convergence theorems are proved. Our results extend the recent results in Zhang et al. [5], S. Takahashi and W. Takahashi [14], Chang et al. [15], Ceng and Yao [6], Li et al. [7] and, Saeidi [8].
2. Preliminaries
In the sequel, we use  and
and  to denote the weak convergence and strong convergence of the sequence
to denote the weak convergence and strong convergence of the sequence  in
in  , respectively.
, respectively.
Definition 2.1.
Let  be a multivalued maximal monotone mapping, then the single-valued mapping
be a multivalued maximal monotone mapping, then the single-valued mapping  defined by
defined by

is called the resolvent operator associated with , where
, where  is any positive number, and
is any positive number, and  is the identity mapping.
is the identity mapping.
Proposition 2.2 (see [5]).
 The resolvent operator
The resolvent operator  associated with
associated with  is single-valued and nonexpansive for all
is single-valued and nonexpansive for all  , that is,
, that is,

 The resolvent operator
The resolvent operator  is 1-inverse-strongly monotone, that is,
is 1-inverse-strongly monotone, that is,

Definition 2.3.
A single-valued mapping  is said to be hemicontinuous, if for any
is said to be hemicontinuous, if for any  , the mapping
, the mapping  converges weakly to
converges weakly to  (as
(as  ).
).
It is well known that every continuous mapping must be hemicontinuous.
Lemma 2.4 (see [16]).
Let  be a real Banach space,
be a real Banach space,  the dual space of
the dual space of  a maximal monotone mapping, and
a maximal monotone mapping, and  a hemicontinuous bounded monotone mapping with
a hemicontinuous bounded monotone mapping with  , then the mapping
, then the mapping  is a maximal monotone mapping.
is a maximal monotone mapping.
For solving the equilibrium problem for bifunction  let us assume that
let us assume that  satisfies the following conditions:
satisfies the following conditions:
 for all
for all  ;
;
 is monotone, that is,
is monotone, that is,  for all
for all  ;
;
for each  ,
,  is concave and upper semicontinuous.
is concave and upper semicontinuous.
for each  ,
,  is convex.
is convex.
A map  is called Lipschitz continuous, if there exists a constant
is called Lipschitz continuous, if there exists a constant  such that
such that

A differentiable function  on a convex set
on a convex set  is called
is called
(i) -convex [6] if
-convex [6] if

where  is the Fréchet derivative of
is the Fréchet derivative of  at
at  ;
;
(ii) -strongly convex [6] if there exists a constant
-strongly convex [6] if there exists a constant  such that
such that

Let  be an equilibrium bifunction satisfying the conditions (H1)–(H4). Let
be an equilibrium bifunction satisfying the conditions (H1)–(H4). Let  be any given positive number. For a given point
be any given positive number. For a given point  , consider the following auxiliary problem for
, consider the following auxiliary problem for (for short,
(for short,  ) to find
) to find  such that
such that

where  is a mapping, and
is a mapping, and  is the Fréchet derivative of a functional
is the Fréchet derivative of a functional  at
at  . Let
. Let  be the mapping such that for each
be the mapping such that for each  ,
,  is the set of solutions of
is the set of solutions of  , that is,
, that is,

Then the following conclusion holds.
Proposition 2.5 (see [6]).
Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  a lower semicontinuous and convex functional. Let
a lower semicontinuous and convex functional. Let  be an equilibrium bifunction satisfying conditions (H1)–(H4). Assume that
be an equilibrium bifunction satisfying conditions (H1)–(H4). Assume that
 is Lipschitz continuous with constant
is Lipschitz continuous with constant  such that
such that

 is affine in the first variable,
is affine in the first variable,
for each fixed  ,
,  is continuous from the weak topology to the weak topology;
is continuous from the weak topology to the weak topology;
 is
is  -strongly convex with constant
-strongly convex with constant  , and its derivative
, and its derivative  is continuous from the weak topology to the strong topology;
is continuous from the weak topology to the strong topology;
for each  , there exists a bounded subset
, there exists a bounded subset  and
and  such that for any
such that for any  , one has
, one has

Then the following hold:
 is single-valued;
is single-valued;
 is nonexpansive if
is nonexpansive if  is Lipschitz continuous with constant
is Lipschitz continuous with constant  such that
such that  ;
;
 ;
;
 is closed and convex.
is closed and convex.
Lemma 2.6 (see [17]).
Let  be a nonempty bounded closed convex subset of
be a nonempty bounded closed convex subset of  , and let
, and let  be a nonexpansive semigroup on
be a nonexpansive semigroup on  , then for any
, then for any 

Lemma 2.7 (see [7]).
Let  be a nonempty bounded closed convex subset of
be a nonempty bounded closed convex subset of  , and let
, and let  be a nonexpansive semigroup on
be a nonexpansive semigroup on  . If
. If  is a sequence in
is a sequence in  such that
such that  and
and  , then
, then  .
.
3. The Main Results
In order to prove the main result, we first give the following lemma.
Lemma 3.1 (see [5]).

 is a solution of variational inclusion (1.2) if and only if
is a solution of variational inclusion (1.2) if and only if  , that is,
, that is,

 If
If  , then
, then  is a closed convex subset in
is a closed convex subset in  .
.
In the sequel, we assume that  satisfy the following conditions:
satisfy the following conditions:
 is a real Hilbert space,
is a real Hilbert space,  is a nonempty closed convex subset;
is a nonempty closed convex subset;
 is a strongly positive linear bounded operator with a coefficient
is a strongly positive linear bounded operator with a coefficient 
 is a contraction mapping with a contraction constant
is a contraction mapping with a contraction constant  ,
,  ,
,  is an
is an  -inverse-strongly monotone mapping, and
-inverse-strongly monotone mapping, and  is a multivalued maximal monotone mapping;
is a multivalued maximal monotone mapping;
 is a nonexpansive semigroup;
is a nonexpansive semigroup;
 is a finite family of bifunctions satisfying conditions (H1)–(H4), and
is a finite family of bifunctions satisfying conditions (H1)–(H4), and  is a finite family of lower semicontinuous and convex functional;
is a finite family of lower semicontinuous and convex functional;
 is a finite family of Lipschitz continuous mappings with constant
is a finite family of Lipschitz continuous mappings with constant  such that
such that

 is affine in the first variable,
is affine in the first variable,
for each fixed  ,
,  is sequentially continuous from the weak topology to the weak topology;
is sequentially continuous from the weak topology to the weak topology;
 is a finite family of
is a finite family of  -strongly convex with constant
-strongly convex with constant  , and its derivative
, and its derivative  is not only continuous from the weak topology to the strong topology but also Lipschitz continuous with constant
is not only continuous from the weak topology to the strong topology but also Lipschitz continuous with constant 
 .
.
In the sequel we always denote by  the set of fixed points of the nonexpansive semi-group
the set of fixed points of the nonexpansive semi-group  ,
,  the set of solutions to the variational inequality (1.2), and MEP(
the set of solutions to the variational inequality (1.2), and MEP( ) the set of solutions to the following auxiliary problem for a system of mixed equilibrium problems:
) the set of solutions to the following auxiliary problem for a system of mixed equilibrium problems:

where

and  ,
,  is the mapping defined by (2.8).
is the mapping defined by (2.8).
In the sequel we denote by  for
for  and
and  .
.
Theorem 3.2.
Let  be the same as above. Let
be the same as above. Let  be a finite family of positive numbers,
be a finite family of positive numbers,  , and
, and  . If
. If  and the following conditions are satisfied:
and the following conditions are satisfied:
for each  , there exists a bounded subset
, there exists a bounded subset  and
and  such that for any
such that for any 


 ,
,  , and
, and  , then
, then
for each  , there is a unique
, there is a unique  such that
such that

the sequence  converges strongly to some point
converges strongly to some point  , provided that
, provided that  is firmly nonexpansive;
is firmly nonexpansive;
 is the unique solution of the following variational inequality
is the unique solution of the following variational inequality

Proof.
We observe that from condition (ii), we can assume, without loss of generality, that  .
.
Since  is a linear bounded self-adjoint operator on
is a linear bounded self-adjoint operator on  , then
, then

Since

this implies that  is positive. Hence we have
is positive. Hence we have

For each given  , let us define the mapping
, let us define the mapping

Firstly we show that the mapping  is a contraction. Indeed, for any
is a contraction. Indeed, for any  , we have
, we have

This implies that  is a contraction mapping. Let
is a contraction mapping. Let  be the unique fixed point of
be the unique fixed point of  . Thus,
. Thus,

is well defined.
Letting  ,
,  , and
, and  , then
, then

We divide the proof of Theorem 3.2 into 8 steps.
Step 1.
First prove that the sequences  , and
, and  are bounded.
are bounded.
-
(a)
Pick
 , since
, since  and
and  , we have
, we have  (3.14)
(3.14)
( ) Since
) Since  and
and  , we have
, we have  , and so
, and so

Letting  ,
,  , we have
, we have

Similarly, we have

Form (3.5), (3.9), (3.14), (3.15), (3.16), and (3.17) we have

So,  . This implies that
. This implies that  is a bounded sequence in
is a bounded sequence in  . Therefore
. Therefore  , and
, and  are all bounded.
are all bounded.
Step 2.
Next we prove that

Since  , then
, then

Hence

From condition (ii), we have

Let  , then
, then  is a nonempty bounded closed convex subset of
is a nonempty bounded closed convex subset of  and
and  -invariant. Since
-invariant. Since  and
and  is bounded, there exists
is bounded, there exists  such that
such that  ; it follows from Lemma 2.6 that
; it follows from Lemma 2.6 that

From (3.22) and (3.23), we have

Step 3.
Next we prove that

In fact, for any given  and
and  , since
, since  is firmly nonexpansive, we have
is firmly nonexpansive, we have

It follows that

From (3.5), we have

Since

and this together with (3.27) and (3.28), it yields

Simplifying it we have

Since  and
and  , by condition (ii), it yields
, by condition (ii), it yields  .
.
Step 4.
Now we prove that for any given 

In fact, it follows from (3.15) that

Substituting (3.33) into (3.28), we obtain

Simplifying it, we have

Since 

 , and
, and  are bounded, these imply that
are bounded, these imply that  .
.
Step 5.
Next we prove that

In fact, since

for the purpose, it is sufficient to prove

( ) First we prove that
) First we prove that  . In fact, since
. In fact, since

we have

Substituting (3.40) into (3.28), it yields that

Simplifying it we have

Since  ,
, 
 ,
,  , and
, and  are bounded, these imply that
are bounded, these imply that  .
.
( ) Next we prove that
) Next we prove that

In fact, since  , so
, so  . This together with (3.25) shows that
. This together with (3.25) shows that  .
.
Step 6.
Next we prove that there exists a subsequence  of
of  such that
such that  , and
, and  is the unique solution of the variational inequality (3.6).
is the unique solution of the variational inequality (3.6).
-
(a)
We first prove that
 . In fact, since
. In fact, since 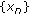 is bounded, there exists a subsequence
is bounded, there exists a subsequence  of
of 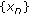 such that
such that 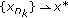 . From Lemma 2.7 and Step 2, we obtain
. From Lemma 2.7 and Step 2, we obtain 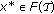 .
. -
(b)
Now we prove that
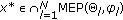 .
.
Since  and noting Step 3, without loss of generality, we may assume that
and noting Step 3, without loss of generality, we may assume that  . Hence for any
. Hence for any  and for any
and for any  , we have
, we have

By the assumptions and by condition (H2) we know that the function  and the mapping
and the mapping  both are convex and lower semicontinuous, hence they are weakly lower semicontinuous. These together with
both are convex and lower semicontinuous, hence they are weakly lower semicontinuous. These together with  and
and  , we have
, we have

That is,

for all  and
and  , hence
, hence  .
.
-
(c)
Now we prove that
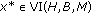 .
.
In fact, since  is
is  -inverse-strongly monotone, it follows from Proposition 1.1 that
-inverse-strongly monotone, it follows from Proposition 1.1 that  is a
is a  -Lipschitz continuous monotone mapping and
-Lipschitz continuous monotone mapping and  (where
(where  is the domain of
is the domain of  ). It follows from Lemma 2.4 that
). It follows from Lemma 2.4 that  is maximal monotone. Let
is maximal monotone. Let  , that is,
, that is,  . Since
. Since  and noting Step 3, without loss of generality, we may assume that
and noting Step 3, without loss of generality, we may assume that  ; in particular, we have
; in particular, we have  . From
. From  , we can prove that
, we can prove that  . Again since
. Again since  , we have
, we have

By virtue of the maximal monotonicity of  , we have
, we have

So,

Since  ,
,  , and
, and  , we have
, we have

Since  is maximal monotone, this implies that
is maximal monotone, this implies that  , that is,
, that is,  , and so
, and so  .
.
-
(d)
Now we prove that
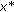 is the unique solution of variational inequality (3.6).
is the unique solution of variational inequality (3.6).
 We first prove that
We first prove that  .
.
Since 

It follows that

Therefore,

Now, replacing  in (3.53) with
in (3.53) with  and letting
and letting  and
and  , we have
, we have  .
.
 Next we prove that
Next we prove that  is the unique solution of the variational inequality (3.6).
is the unique solution of the variational inequality (3.6).
Since

we have

Hence for any  we have,
we have,

then

It is easily seen that  is monotone. Thus from (3.57) we have that
is monotone. Thus from (3.57) we have that

Now, in (3.58) replacing  by
by  and letting
and letting  and
and  , from (3.36), we have
, from (3.36), we have

So, we have

It follows from [18, Theorem  ] that the solution of the variational inequality (3.6) is unique, that is,
] that the solution of the variational inequality (3.6) is unique, that is,  is a unique solution of (3.6).
is a unique solution of (3.6).
Step 7.
Next we prove that

( ) First, we prove that
) First, we prove that

Indeed, there exists a subsequence  of
of  such that
such that

We may also assume that  . This together with (3.22) and (3.36) shows that
. This together with (3.22) and (3.36) shows that  . Since
. Since  , we have
, we have  . Again by the same method as given in Step 6 we can prove that
. Again by the same method as given in Step 6 we can prove that  . So, we have
. So, we have

( ) Now we prove that
) Now we prove that

From  and (a), we have
and (a), we have

Step 8.
Finally we prove that

Indeed, from (3.5), (3.15), and (3.17), we have

This implies that

Combining (3.61) and (3.69), we obtain that  .
.
This completes the proof of Theorem 3.2.
Corollary 3.3.
Let  be the same as in Theorem 3.2. Let
be the same as in Theorem 3.2. Let  be a finite family of positive parameter,
be a finite family of positive parameter,  and
and  . If
. If  and conditions (i) and (ii) in Theorem 3.2 are satisfied, then
and conditions (i) and (ii) in Theorem 3.2 are satisfied, then
for each  there is a unique
there is a unique  such that
such that

the sequence  converges strongly to some point
converges strongly to some point  , provided that
, provided that  is firmly nonexpansive;
is firmly nonexpansive;
 is the unique solution of variational inequality (3.6).
is the unique solution of variational inequality (3.6).
Proof.
Taking  in Theorem 3.2, where
in Theorem 3.2, where  is the indicator function of
is the indicator function of  , that is,
, that is,

then the variational inclusion problem (1.2) is equivalent to variational inequality (1.4), that is, to find  such that
such that

Again, since  , then
, then  . Therefore we have
. Therefore we have

The conclusion of Corollary 3.3 can be obtained from Theorem 3.2 immediately.
4. Applications to Optimization Problem
Let  be a real Hilbert space,
be a real Hilbert space,  a nonempty closed convex subset of
a nonempty closed convex subset of  a strongly positive linear bounded operator with a constant
a strongly positive linear bounded operator with a constant  , and
, and  a nonexpansive mapping. In this section we will utilize the results presented in Section 3 to study the following optimization problem:
a nonexpansive mapping. In this section we will utilize the results presented in Section 3 to study the following optimization problem:

where  is the set of fixed points of
is the set of fixed points of  in
in  and
and  is a potential function for
is a potential function for  (i.e.,
(i.e.,  ,
,  ), where
), where  is a contractive mapping with a contractive constant
is a contractive mapping with a contractive constant  . We have the following theorem.
. We have the following theorem.
Theorem 4.1.
Let  be the same as above. Let
be the same as above. Let  be sequences in
be sequences in  satisfying condition (ii) in Theorem 3.2. If
satisfying condition (ii) in Theorem 3.2. If  is a nonempty compact subset of
is a nonempty compact subset of  , then for each
, then for each  there is a unique
there is a unique  such that
such that

and the sequence  converges strongly to some point
converges strongly to some point  which is the unique minimal point of optimization problem (4.1).
which is the unique minimal point of optimization problem (4.1).
Proof.
Taking  ,
,  ,
, 

 ,
,  ,
,  in Corollary 3.3, hence we have
in Corollary 3.3, hence we have  ,
, ,
,
 ,
,  ,
,  ,
,  ,
,  . Hence from Corollary 3.3 we know that the sequence
. Hence from Corollary 3.3 we know that the sequence  defined by (4.2) converges strongly to some point
defined by (4.2) converges strongly to some point  which is the unique solution of the following variational inequality:
which is the unique solution of the following variational inequality:

Since  is nonexpansive, then
is nonexpansive, then  is convex. Again by the assumption that
is convex. Again by the assumption that  is compact, therefore it is a compact and convex subset of
is compact, therefore it is a compact and convex subset of  , and
, and  is a continuous mapping. By virtue of the well-known Weierstrass theorem, there exists a point
is a continuous mapping. By virtue of the well-known Weierstrass theorem, there exists a point  which is a minimal point of optimization problem (4.1). As is known to all, (4.3) is the optimality necessary condition [19] for the optimization problem (4.1). Therefore we also have
which is a minimal point of optimization problem (4.1). As is known to all, (4.3) is the optimality necessary condition [19] for the optimization problem (4.1). Therefore we also have

Since  is the unique solution of (4.3), we have
is the unique solution of (4.3), we have  .
.
This completes the proof of Theorem 4.1.
References
Chang SS: Set-valued variational inclusions in Banach spaces. Journal of Mathematical Analysis and Applications 2000, 248(2):438–454. 10.1006/jmaa.2000.6919
Chang SS: Existence and approximation of solutions for set-valued variational inclusions in Banach space. Nonlinear Analysis: Theory, Methods & Applications 2001, 47(1):583–594. 10.1016/S0362-546X(01)00203-6
Demyanov VF, Stavroulakis GE, Polyakova LN, Panagiotopoulos PD: Quasidifferentiability and Nonsmooth Modelling in Mechanics, Engineering and Economics, Nonconvex Optimization and Its Applications. Volume 10. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1996:xviii+348.
Lions J-L, Stampacchia G: Variational inequalities. Communications on Pure and Applied Mathematics 1967, 20: 493–519. 10.1002/cpa.3160200302
Zhang S-s, Lee JHW, Chan CK: Algorithms of common solutions to quasi variational inclusion and fixed point problems. Applied Mathematics and Mechanics 2008, 29(5):571–581. 10.1007/s10483-008-0502-y
Ceng L-C, Yao J-C: A hybrid iterative scheme for mixed equilibrium problems and fixed point problems. Journal of Computational and Applied Mathematics 2008, 214(1):186–201. 10.1016/j.cam.2007.02.022
Li S, Li L, Su Y: General iterative methods for a one-parameter nonexpansive semigroup in Hilbert space. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(9):3065–3071. 10.1016/j.na.2008.04.007
Saeidi S: Iterative algorithms for finding common solutions of variational inequalities and systems of equilibrium problems and fixed points of families and semigroups of nonexpansive mappings. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(12):4195–4208. 10.1016/j.na.2008.09.009
Yao Y, Cho YJ, Chen R: An iterative algorithm for solving fixed point problems, variational inequality problems and mixed equilibrium problems. Nonlinear Analysis: Theory, Methods & Applications 2009, 71(7–8):3363–3373. 10.1016/j.na.2009.01.236
Kumam W, Kumam P: Hybrid iterative scheme by a relaxed extragradient method for solutions of equilibrium problems and a general system of variational inequalities with application to optimization. Nonlinear Analysis: Hybrid Systems 2009, 3(4):640–656. 10.1016/j.nahs.2009.05.007
Colao V, Acedo GL, Marino G: An implicit method for finding common solutions of variational inequalities and systems of equilibrium problems and fixed points of infinite family of nonexpansive mappings. Nonlinear Analysis: Theory, Methods & Applications 2009, 71(7–8):2708–2715. 10.1016/j.na.2009.01.115
He H, Liu S, Zhou H: An explicit method for finding common solutions of variational inequalities and systems of equilibrium problems and fixed points of an infinite family of nonexpansive mappings. Nonlinear Analysis: Theory, Methods & Applications 2010, 72(6):3124–3135. 10.1016/j.na.2009.12.002
Hu CS, Cai G: Viscosity approximation schemes for fixed point problems and equilibrium problems and variational inequality problems. Nonlinear Analysis: Theory, Methods & Applications 2010, 72(3–4):1792–1808. 10.1016/j.na.2009.09.021
Takahashi S, Takahashi W: Viscosity approximation methods for equilibrium problems and fixed point problems in Hilbert spaces. Journal of Mathematical Analysis and Applications 2007, 331(1):506–515. 10.1016/j.jmaa.2006.08.036
Chang SS, Lee HWJ, Chan CK: A new method for solving equilibrium problem fixed point problem and variational inequality problem with application to optimization. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(9):3307–3319. 10.1016/j.na.2008.04.035
Dan P: Nolinear Mappings of Monotone Type. Sijthoff and Noordhoff, Alphen aan den Rijn, The Netherlands; 1978.
Shimizu T, Takahashi W: Strong convergence to common fixed points of families of nonexpansive mappings. Journal of Mathematical Analysis and Applications 1997, 211(1):71–83. 10.1006/jmaa.1997.5398
Marino G, Xu H-K: A general iterative method for nonexpansive mappings in Hilbert spaces. Journal of Mathematical Analysis and Applications 2006, 318(1):43–52. 10.1016/j.jmaa.2005.05.028
Xu HK: An iterative approach to quadratic optimization. Journal of Optimization Theory and Applications 2003, 116(3):659–678. 10.1023/A:1023073621589
Acknowledgment
The authors would like to express their thanks to the referees for their valuable suggestions and comments.
Author information
Authors and Affiliations
Corresponding authors
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Liu, M., Chang, S. & Zuo, P. An Algorithm for Finding a Common Solution for a System of Mixed Equilibrium Problem, Quasivariational Inclusion Problem, and Fixed Point Problem of Nonexpansive Semigroup. J Inequal Appl 2010, 895907 (2010). https://doi.org/10.1155/2010/895907
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/895907
 , since
, since  and
and  , we have
, we have 
 . In fact, since
. In fact, since 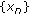 is bounded, there exists a subsequence
is bounded, there exists a subsequence  of
of 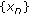 such that
such that 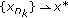 . From Lemma 2.7 and Step 2, we obtain
. From Lemma 2.7 and Step 2, we obtain 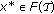 .
.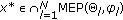 .
.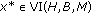 .
.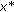 is the unique solution of variational inequality (3.6).
is the unique solution of variational inequality (3.6).