- Research Article
- Open access
- Published:
Modified Block Iterative Algorithm for Solving Convex Feasibility Problems in Banach Spaces
Journal of Inequalities and Applications volume 2010, Article number: 869684 (2010)
Abstract
The purpose of this paper is to use the modified block iterative method to propose an algorithm for solving the convex feasibility problems for an infinite family of quasi- -asymptotically nonexpansive mappings. Under suitable conditions some strong convergence theorems are established in uniformly smooth and strictly convex Banach spaces with Kadec-Klee property. The results presented in the paper improve and extend some recent results.
-asymptotically nonexpansive mappings. Under suitable conditions some strong convergence theorems are established in uniformly smooth and strictly convex Banach spaces with Kadec-Klee property. The results presented in the paper improve and extend some recent results.
1. Introduction
The problem of finding a point in the intersection of closed and convex subsets  of a Banach space is a frequently appearing problem in diverse areas of mathematics and physical sciences. This problem is commonly referred to as theconvex feasibility problem (CFP). There is a considerable investigation on (CFP) in the framework of Hilbert spaces which captures applications in various disciplines such as image restoration, computer tomograph, and radiation therapy treatment planning [1]. The advantage of a Hilbert space
of a Banach space is a frequently appearing problem in diverse areas of mathematics and physical sciences. This problem is commonly referred to as theconvex feasibility problem (CFP). There is a considerable investigation on (CFP) in the framework of Hilbert spaces which captures applications in various disciplines such as image restoration, computer tomograph, and radiation therapy treatment planning [1]. The advantage of a Hilbert space  is that the projection
is that the projection  onto a closed convex subset
onto a closed convex subset  of
of  is nonexpansive. So projection methods have dominated in the iterative approaches to (CFP) in Hilbert space. In 1993, Kitahara and Takahashi [2] deal with the convex feasibility problem by convex combinations of sunny nonexpansive retractions in uniformly convex Banach space (see also, O'Hara et al. [3] and Chang et al. [4]). It is known that if
is nonexpansive. So projection methods have dominated in the iterative approaches to (CFP) in Hilbert space. In 1993, Kitahara and Takahashi [2] deal with the convex feasibility problem by convex combinations of sunny nonexpansive retractions in uniformly convex Banach space (see also, O'Hara et al. [3] and Chang et al. [4]). It is known that if  is a nonempty closed convex subset of a smooth, reflexive, and strictly convex Banach space
is a nonempty closed convex subset of a smooth, reflexive, and strictly convex Banach space  , then the generalized projection
, then the generalized projection from
from  onto
onto  is relatively nonexpansive. In 2005, Matsushita and Takahashi [5] reformulated the definition of the notion and obtained weak and strong convergence theorems to approximate a fixed point of a single relatively nonexpansive mapping. Recently, Qin et al. [6], Zhou and Tan [7], Wattanawitoon and Kumam [8], Li and Su [9], and Takahashi and Zembayashi [10] extend the notion from relatively nonexpansive mappings or quasi-
is relatively nonexpansive. In 2005, Matsushita and Takahashi [5] reformulated the definition of the notion and obtained weak and strong convergence theorems to approximate a fixed point of a single relatively nonexpansive mapping. Recently, Qin et al. [6], Zhou and Tan [7], Wattanawitoon and Kumam [8], Li and Su [9], and Takahashi and Zembayashi [10] extend the notion from relatively nonexpansive mappings or quasi- -nonexpansive mappings to quasi-
-nonexpansive mappings to quasi- -asymptotically nonexpansive mappings and also prove some weak and strong convergence theorems to approximate a common fixed point of finite or infinite family of quasi-
-asymptotically nonexpansive mappings and also prove some weak and strong convergence theorems to approximate a common fixed point of finite or infinite family of quasi- -nonexpansive mappings or quasi-
-nonexpansive mappings or quasi- -asymptotically nonexpansive mappings.
-asymptotically nonexpansive mappings.
It should be noted that theblock iterative algorithm is a method which often used by many authors to solve the convex feasibility problem (see, e.g., Kikkawa and Takahashi [11], Aleyner and Reich [12]). Recently, some authors by using the block iterative scheme to establish strong convergence theorems for a finite family of relativity nonexpansive mappings in Hilbert space or finite-dimensional Banach space (see, e.g., Aleyner and Reich [12], Plubtieng and Ungchittrakool [13, 14]) or uniformly smooth and uniformly convex Banach spaces (see, e.g., Sahu et al. [15] and Ceng et al. [16–18]).
Motivated and inspired by these facts, the purpose of this paper is to use the modified block iterative method to propose an iterative algorithm for solvingthe convex feasibility problems for an infinite family of quasi- -asymptotically nonexpansive. Under suitable conditions some strong convergence theorems are established in a uniformly smooth and strictly convex Banach space with Kadec-Klee property. The results presented in the paper improve and extend the corresponding results in Aleyner and Reich [12], Plubtieng and Ungchittrakool [13, 14], and Chang et al. [19].
-asymptotically nonexpansive. Under suitable conditions some strong convergence theorems are established in a uniformly smooth and strictly convex Banach space with Kadec-Klee property. The results presented in the paper improve and extend the corresponding results in Aleyner and Reich [12], Plubtieng and Ungchittrakool [13, 14], and Chang et al. [19].
2. Preliminaries
Throughout this paper we assume that  is a real Banach space with the dual
is a real Banach space with the dual  and
and  is the normalized duality mapping defined by
is the normalized duality mapping defined by

In the sequel, we use  to denote the set of fixed points of a mapping
to denote the set of fixed points of a mapping  and use
and use  and
and  to denote the set of all real numbers and the set of all nonnegative real numbers, respectively. We also denote by
to denote the set of all real numbers and the set of all nonnegative real numbers, respectively. We also denote by  and
and  the strong convergence and weak convergence of a sequence
the strong convergence and weak convergence of a sequence  respectively.
respectively.
A Banach space  is said to bestrictly convex if
is said to bestrictly convex if  for all
for all  with
with  .
.  is said to be uniformly convex if, for each
is said to be uniformly convex if, for each  , there exists
, there exists  such that
such that  for all
for all  with
with 
 is said to be smooth if the limit
is said to be smooth if the limit

exists for all  .
.  is said to be uniformly smooth if the above limit exists uniformly in
is said to be uniformly smooth if the above limit exists uniformly in  .
.
Remark 2.1.
The following basic properties can be found in Cioranescu [20].
-
(i)
If
 is a uniformly smooth Banach space, then
is a uniformly smooth Banach space, then 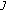 is uniformly continuous on each bounded subset of
is uniformly continuous on each bounded subset of 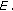
-
(ii)
If
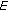 is a reflexive and strictly convex Banach space, then
is a reflexive and strictly convex Banach space, then 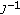 is hemicontinuous, that is,
is hemicontinuous, that is, 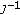 is norm-
is norm- -continuous.
-continuous. -
(iii)
If
 is a smooth, strictly convex, and reflexive Banach space, then the normalized duality mapping
is a smooth, strictly convex, and reflexive Banach space, then the normalized duality mapping  is single-valued, one-to-one, and onto.
is single-valued, one-to-one, and onto. -
(iv)
A Banach space
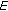 is uniformly smooth if and only if
is uniformly smooth if and only if 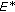 is uniformly convex.
is uniformly convex. -
(v)
Each uniformly convex Banach space
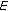 has the Kadec-Klee property, that is, for any sequence
has the Kadec-Klee property, that is, for any sequence 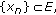 if
if 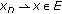 and
and 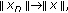 then
then 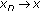 .
.
Next we assume that  is a smooth, strictly convex, and reflexive Banach space and
is a smooth, strictly convex, and reflexive Banach space and  is a nonempty closed convex subset of
is a nonempty closed convex subset of  . In the sequel we always use
. In the sequel we always use  to denote the Lyapunov functional defined by
to denote the Lyapunov functional defined by

It is obvious from the definition of  that
that

Following Alber [21], the generalized projection is defined by
is defined by

Lemma 2.2 (see [21]).
Let  be a smooth, strictly convex, and reflexive Banach space and
be a smooth, strictly convex, and reflexive Banach space and  a nonempty closed convex subset of
a nonempty closed convex subset of  . Then the following conclusions hold:
. Then the following conclusions hold:
(a) for all
for all  and
and  ;
;
-
(b)
if
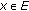 and
and 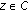 , then
, then 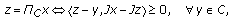 (26)
(26)
-
(c)
for
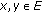 ,
, 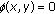 if and only if
if and only if 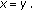
Remark 2.3.
If  is a real Hilbert space
is a real Hilbert space  , then
, then  and
and  is the metric projection
is the metric projection  of
of  onto
onto  .
.
Let  be a smooth, strictly convex, and reflexive Banach space,
be a smooth, strictly convex, and reflexive Banach space,  a nonempty closed convex subset of
a nonempty closed convex subset of  ,
,  a mapping, and
a mapping, and  the set of fixed points of
the set of fixed points of  . A point
. A point  is said to be an asymptotic fixed point of
is said to be an asymptotic fixed point of  if there exists a sequence
if there exists a sequence  such that
such that  and
and  We denoted the set of all asymptotic fixed points of
We denoted the set of all asymptotic fixed points of  by
by  .
.
Definition 2.4.
 A mapping
A mapping  is said to berelatively nonexpansive [5] if
is said to berelatively nonexpansive [5] if  , and
, and

 A mapping
A mapping  is said to beclosed if for any sequence
is said to beclosed if for any sequence  with
with  and
and  , then
, then  .
.
Definition 2.5.
 A mapping
A mapping  is said to bequasi-
is said to bequasi- -nonexpansive if
-nonexpansive if  and
and

 A mapping
A mapping  is is said to be quasi- ϕ -asymptotically nonexpansive [7], if
is is said to be quasi- ϕ -asymptotically nonexpansive [7], if  and there exists a real sequence
and there exists a real sequence  with
with  such that
such that

Remark 2.6.
 From the definition, it is easy to know that each relatively nonexpansive mapping is closed.
From the definition, it is easy to know that each relatively nonexpansive mapping is closed.
 The class of quasi-
The class of quasi- -asymptotically nonexpansive mappings contains properly the class of quasi-
-asymptotically nonexpansive mappings contains properly the class of quasi- -nonexpansive mappings as a subclass and the class of quasi-
-nonexpansive mappings as a subclass and the class of quasi- -nonexpansive mappings contains properly the class of relatively nonexpansive mappings as a subclass, but the converse may be not true.
-nonexpansive mappings contains properly the class of relatively nonexpansive mappings as a subclass, but the converse may be not true.
Next, we give some examples which are closed and quasi- -asymptotically nonexpansive mappings.
-asymptotically nonexpansive mappings.
Example 2.7 (see [7]).
Let  be a uniformly smooth and strictly convex Banach space and
be a uniformly smooth and strictly convex Banach space and  a maximal monotone mapping such that
a maximal monotone mapping such that  (the set of zero points of
(the set of zero points of  ) is nonempty. Then the mapping
) is nonempty. Then the mapping  is closed and quasi-
is closed and quasi- -asymptotically nonexpansive from
-asymptotically nonexpansive from  onto
onto  and
and 
Example 2.8.
Let  be the generalized projection from a smooth, strictly convex and reflexive Banach space
be the generalized projection from a smooth, strictly convex and reflexive Banach space  onto a nonempty closed convex subset
onto a nonempty closed convex subset  . Then
. Then  is relative nonexpansive, which in turn is a closed and quasi-
is relative nonexpansive, which in turn is a closed and quasi- -nonexpansive mapping, and so it is a closed and quasi-
-nonexpansive mapping, and so it is a closed and quasi- -asymptotically nonexpansive mapping.
-asymptotically nonexpansive mapping.
Let  be a uniformly convex Banach space,
be a uniformly convex Banach space,  be a positive number and
be a positive number and  be a closed ball of
be a closed ball of  . Then, for any given subset
. Then, for any given subset  and for any positive numbers
and for any positive numbers  with
with  , there exists a continuous, strictly increasing, and convex function
, there exists a continuous, strictly increasing, and convex function  with
with  such that, for any
such that, for any  with
with  ,
,

Lemma 2.10.
Let  be a uniformly convex Banach space,
be a uniformly convex Banach space,  a positive number and
a positive number and  a closed ball of
a closed ball of  . Then, for any given sequence
. Then, for any given sequence  and for any given sequence
and for any given sequence  of positive numbers with
of positive numbers with  there exists a continuous, strictly increasing, and convex function
there exists a continuous, strictly increasing, and convex function  with
with  such that for any positive integers
such that for any positive integers  with
with 

Proof.
Since  and
and  for all
for all  with
with  , we have
, we have

Hence, for any given  and any given positive integers
and any given positive integers  with
with  it follows from (2.12) that there exists a positive integer
it follows from (2.12) that there exists a positive integer  such that
such that  Letting
Letting  , by Lemma 2.9, we have
, by Lemma 2.9, we have

Since  is arbitrary, the conclusion of Lemma 2.10 is proved.
is arbitrary, the conclusion of Lemma 2.10 is proved.
Lemma 2.11.
Let  be a real uniformly smooth and strictly convex Banach space with Kadec-Klee property, and
be a real uniformly smooth and strictly convex Banach space with Kadec-Klee property, and  a nonempty closed convex subset of
a nonempty closed convex subset of  . Let
. Let  be a closed and quasi-
be a closed and quasi- -asymptotically nonexpansive mapping with a sequence
-asymptotically nonexpansive mapping with a sequence  . Then
. Then  is a closed convex subset of
is a closed convex subset of  .
.
Proof.
Letting  be a sequence in
be a sequence in  with
with  (as
(as  ), we prove that
), we prove that  In fact, from the definition of
In fact, from the definition of  we have
we have

Therefore we have

that is,  .
.
Next we prove that  is convex. For any
is convex. For any  , putting
, putting  we prove that
we prove that  Indeed, in view of the definition of
Indeed, in view of the definition of  we have
we have

Since  , we have
, we have  (as
(as  ). From (2.4) we have
). From (2.4) we have  Consequently
Consequently  This implies that
This implies that  is a bounded sequence. Since
is a bounded sequence. Since  is reflexive,
is reflexive,  is also reflexive. So we can assume that
is also reflexive. So we can assume that

Again since  is reflexive, we have
is reflexive, we have  . Therefore there exists
. Therefore there exists  such that
such that  . By virtue of the weakly lower semicontinuity of norm
. By virtue of the weakly lower semicontinuity of norm  we have
we have

that is,  which implies that
which implies that  . Thus from (2.17) we have
. Thus from (2.17) we have  Since
Since  and
and  has the Kadec-Klee property, we have
has the Kadec-Klee property, we have  . Since
. Since  is uniformly smooth and strictly convex, by Remark 2.1(ii) it yields that
is uniformly smooth and strictly convex, by Remark 2.1(ii) it yields that  is hemi-continuous. Therefore
is hemi-continuous. Therefore  . Again since
. Again since  by using the Kadec-Klee property of
by using the Kadec-Klee property of  , we have
, we have  . This implies that
. This implies that  . Since
. Since  is closed, we have
is closed, we have  . This completes the proof of Lemma 2.11.
. This completes the proof of Lemma 2.11.
3. Main Results
In this section, we will use the modified block iterative method to propose an iterative algorithm for solving the convex feasibility problem for an infinite family of quasi asymptotically nonexpansive mappings in uniformly smooth and strictly convex Banach spaces with the Kadec-Klee property.
asymptotically nonexpansive mappings in uniformly smooth and strictly convex Banach spaces with the Kadec-Klee property.
Definition 3.1.
 Let
Let  be a sequence of mappings.
be a sequence of mappings.  is said to bea family of uniformly quasi
is said to bea family of uniformly quasi asymptotically nonexpansive mappings, if
asymptotically nonexpansive mappings, if  and there exists a sequence
and there exists a sequence  with
with  such that for each
such that for each 

 A mapping
A mapping  is said to be uniformly
is said to be uniformly -Lipschitz continuous, if there exists a constant
-Lipschitz continuous, if there exists a constant  such that
such that

Theorem 3.2.
Let  be a uniformly smooth and strictly convex Banach space with Kleac-Klee property and
be a uniformly smooth and strictly convex Banach space with Kleac-Klee property and  a nonempty closed convex subsets of
a nonempty closed convex subsets of  . Let
. Let  be an infinite family of closed and uniformly quasi-
be an infinite family of closed and uniformly quasi- -asymptotically nonexpansive mappings with a sequence
-asymptotically nonexpansive mappings with a sequence  and
and  Suppose that for each
Suppose that for each  is uniformly
is uniformly  -Lipschitz continuous and that
-Lipschitz continuous and that  is a nonempty and bounded subset in
is a nonempty and bounded subset in  Let
Let  be the sequence generated by
be the sequence generated by

where  ,
,  is the generalized projection of
is the generalized projection of  onto the set
onto the set  and for each
and for each  ,
,  is a sequence in
is a sequence in  satisfying the following conditions:
satisfying the following conditions:
(a) for all
for all 
(b) for all
for all 
Then  converges strongly to
converges strongly to 
Proof.
We divide the proof of Theorem 3.2 into five steps.
Step 1.
We first prove that  and
and  both are closed and convex subset of
both are closed and convex subset of  for all
for all  .
.
In fact, It follows from Lemma 2.11 that  is closed and convex. Therefore
is closed and convex. Therefore  is a closed and convex subset in
is a closed and convex subset in  . Furthermore, it is obvious that
. Furthermore, it is obvious that  is closed and convex. Suppose that
is closed and convex. Suppose that  is closed and convex for some
is closed and convex for some  . Since the inequality
. Since the inequality  is equivalent to
is equivalent to

therefore, we have

This implies that  is closed and convex. The desired conclusions are proved. These in turn show that
is closed and convex. The desired conclusions are proved. These in turn show that  and
and  are well defined.
are well defined.
Step 2.
We prove that  is a bounded sequence in
is a bounded sequence in  .
.
By the definition of  , we have
, we have  for all
for all  It follows from Lemma 2.2(a) that
It follows from Lemma 2.2(a) that

This implies that  is bounded. By virtue of (2.4),
is bounded. By virtue of (2.4),  is bounded. Denote
is bounded. Denote

Step 3.
Next, we prove that  for all
for all  .
.
It is obvious that  Suppose that
Suppose that  for some
for some  . Since
. Since  is uniformly smooth,
is uniformly smooth,  is uniformly convex. For any given
is uniformly convex. For any given  and for any positive integer
and for any positive integer  , from Lemma 2.10 we have
, from Lemma 2.10 we have

Hence  and so
and so  for all
for all  . By the way, from the definition of
. By the way, from the definition of  , (2.4), and (3.7), it is easy to see that
, (2.4), and (3.7), it is easy to see that

Step 4.
Now, we prove that  converges strongly to some point
converges strongly to some point  .
.
In fact, since  is bounded in
is bounded in  and
and  is reflexive, we may assume that
is reflexive, we may assume that  . Again since
. Again since  is closed and convex for each
is closed and convex for each  , it is easy to see that
, it is easy to see that  for each
for each  . Since
. Since  , from the definition of
, from the definition of  , we have
, we have

Since

we have

This implies that  that is,
that is,  In view of the Kadec-Klee property of
In view of the Kadec-Klee property of  , we obtain that
, we obtain that

Now we prove that  .In fact, by the construction of
.In fact, by the construction of  we have that
we have that  and
and  Therefore by Lemma 2.2(a) we have
Therefore by Lemma 2.2(a) we have

In view of  and note the construction of
and note the construction of  we obtain that
we obtain that

From (2.4) it yields  Since
Since  we have
we have

Hence we have

This implies that  is bounded in
is bounded in  Since
Since  is reflexive, and so
is reflexive, and so  is reflexive, we can assume that
is reflexive, we can assume that  In view of the reflexive of
In view of the reflexive of  we see that
we see that  . Hence there exists
. Hence there exists  such that
such that  . Since
. Since

Taking  on the both sides of equality above and in view of the weak lower semicontinuity of norm
on the both sides of equality above and in view of the weak lower semicontinuity of norm  it yields that
it yields that

that is,  This implies that
This implies that  and so
and so  . It follows from (3.17) and the Kadec-Klee property of
. It follows from (3.17) and the Kadec-Klee property of  that
that  (as
(as  ). Note that
). Note that  is hemi-continuous, it yields that
is hemi-continuous, it yields that  It follows from (3.16) and the Kadec-Klee property of
It follows from (3.16) and the Kadec-Klee property of  that
that

From (3.13) and (3.20) we have that

Since  is uniformly continuous on any bounded subset of
is uniformly continuous on any bounded subset of  , we have
, we have

For any  and any
and any  , it follows from (3.8), (3.13), and (3.20) that
, it follows from (3.8), (3.13), and (3.20) that

In view of condition (b)  , we see that
, we see that

It follows from the property of  that
that

Since  and
and  is uniformly continuous, it yieads
is uniformly continuous, it yieads  Hence from (3.25) we have
Hence from (3.25) we have

Since  is hemi-continuous, it follows that
is hemi-continuous, it follows that

On the other hand, for each  we have
we have

This together with (3.27) shows that

Furthermore, by the assumption that for each  ,
,  is uniformly
is uniformly  -Lipschitz continuous, hence we have
-Lipschitz continuous, hence we have

This together with (3.13) and (3.29), yields  . Hence from (3.29) we have
. Hence from (3.29) we have  , that is,
, that is,  . In view of (3.29) and the closeness of
. In view of (3.29) and the closeness of  , it yields that
, it yields that  . This implies that
. This implies that  .
.
Step 5.
Finally we prove that  .
.
Let  . Since
. Since  and
and  , we have
, we have

This implies that

In view of the definition of  , from (3.32) we have
, from (3.32) we have  . Therefore,
. Therefore,  . This completes the proof of Theorem 3.2.
. This completes the proof of Theorem 3.2.
The following theorem can be obtained from Theorem 3.2 immediately.
Theorem 3.3.
Let  be a uniformly smooth and strictly convex Banach space with Kadec-Klee property ,
be a uniformly smooth and strictly convex Banach space with Kadec-Klee property ,  a nonempty closed convex subset of
a nonempty closed convex subset of  . Let
. Let  be an infinite family of closed and quasi-
be an infinite family of closed and quasi- -nonexpansive mappings. Suppose that
-nonexpansive mappings. Suppose that  is a nonempty subset in
is a nonempty subset in  . Let
. Let  be the sequence generated by
be the sequence generated by

where  for each
for each  , is a sequence in
, is a sequence in  satisfying the following conditions:
satisfying the following conditions:
(a) for all
for all  ;
;
(b) for all
for all  .
.
Then  converges strongly to
converges strongly to  .
.
Proof.
Since  is an infinite family of closed quasi-
is an infinite family of closed quasi- -nonexpansive mappings, it is an infinite family of closed and uniformly quasi-
-nonexpansive mappings, it is an infinite family of closed and uniformly quasi- -asymptotically nonexpansive mappings with sequence
-asymptotically nonexpansive mappings with sequence  . Hence
. Hence  . Therefore the conditions appearing in Theorem 3.2:
. Therefore the conditions appearing in Theorem 3.2:  is a bounded subset in
is a bounded subset in  " and "for each
" and "for each  ,
,  is uniformly
is uniformly  -Lipschitz continuous" are of no use here. In fact, by the same methods as given in the proofs of (3.13), (3.20) and (3.29), we can prove that
-Lipschitz continuous" are of no use here. In fact, by the same methods as given in the proofs of (3.13), (3.20) and (3.29), we can prove that  ,
,  and
and  (as
(as  ) for each
) for each  . By virtue of the closeness of mapping
. By virtue of the closeness of mapping  for each
for each  , it yields that
, it yields that  for each
for each  , that is,
, that is,  . Therefore all conditions in Theorem 3.2 are satisfied. The conclusion of Theorem 3.3 is obtained from Theorem 3.2 immediately.
. Therefore all conditions in Theorem 3.2 are satisfied. The conclusion of Theorem 3.3 is obtained from Theorem 3.2 immediately.
Remark 3.4.
Theorems 3.2 and 3.3 improve and extend the corresponding results in Aleyner and Reich [12], Plubtieng and Ungchittrakool [13, 14] and Chang et al. [19] in the following aspects.
-
(a)
For the framework of spaces, we extend the space from a uniformly smooth and uniformly convex Banach space to a uniformly smooth and strictly convex Banach space with the Kadec-Klee property (note that each uniformly convex Banach space must have the Kadec-Klee property).
-
(b)
For the mappings, we extend the mappings from nonexpansive mappings, relatively nonexpansive mappings or quasi-
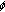 -nonexpansive mapping to an infinite family of quasi-
-nonexpansive mapping to an infinite family of quasi-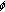 -asymptotically mappings;
-asymptotically mappings; -
(c)
For the algorithms, we propose a new modified block iterative algorithms which are different from ones given in [12–14, 19] and others.
References
Combettes PL: The convex feasibility problem in inage recovery. In Advances in Imaging and Electron Physics. Volume 95. Edited by: Hawkes P. Academic Press, New York, NY, USA; 1996:155–270.
Kitahara S, Takahashi W: Image recovery by convex combinations of sunny nonexpansive retractions. Topological Methods in Nonlinear Analysis 1993, 2(2):333–342.
O'Hara JG, Pillay P, Xu H-K: Iterative approaches to convex feasibility problems in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2006, 64(9):2022–2042. 10.1016/j.na.2005.07.036
Chang S-S, Yao J-C, Kim JK, Yang L: Iterative approximation to convex feasibility problems in Banach space. Fixed Point Theory and Applications 2007, 2007:-19.
Matsushita S, Takahashi W: A strong convergence theorem for relatively nonexpansive mappings in a Banach space. Journal of Approximation Theory 2005, 134(2):257–266. 10.1016/j.jat.2005.02.007
Qin X, Cho YJ, Kang SM: Convergence theorems of common elements for equilibrium problems and fixed point problems in Banach spaces. Journal of Computational and Applied Mathematics 2009, 225(1):20–30. 10.1016/j.cam.2008.06.011
Zhou H, Tan B: Convergence theorems of a modified hybrid algorithm for a family of quasi--asymptotically nonexpansive mappings. Journal of Applied Mathematics and Computing. In press
Wattanawitoon K, Kumam P: Strong convergence theorems by a new hybrid projection algorithm for fixed point problems and equilibrium problems of two relatively quasi-nonexpansive mappings. Nonlinear Analysis: Hybrid Systems 2009, 3(1):11–20. 10.1016/j.nahs.2008.10.002
Li HY, Su YF: Strong convergence theorems by a new hybrid for equilibrium problems and variational inequality problems. Nonlinear Analysis: Theory, Methods & Applications 2009, 72(2):847–855.
Takahashi W, Zembayashi K: Strong and weak convergence theorems for equilibrium problems and relatively nonexpansive mappings in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(1):45–57. 10.1016/j.na.2007.11.031
Kikkawa M, Takahashi W: Approximating fixed points of nonexpansive mappings by the block iterative method in Banach spaces. International Journal of Computational and Numerical Analysis and Applications 2004, 5(1):59–66.
Aleyner A, Reich S: Block-iterative algorithms for solving convex feasibility problems in Hilbert and in Banach spaces. Journal of Mathematical Analysis and Applications 2008, 343(1):427–435. 10.1016/j.jmaa.2008.01.087
Plubtieng S, Ungchittrakool K: Hybrid iterative methods for convex feasibility problems and fixed point problems of relatively nonexpansive mappings in Banach spaces. Fixed Point Theory and Applications 2008, 2008:-19.
Plubtieng S, Ungchittrakool K: Strong convergence theorems of block iterative methods for a finite family of relatively nonexpansive mappings in Banach spaces. Journal of Nonlinear and Convex Analysis 2007, 8(3):431–450.
Sahu DR, Xu H-K, Yao J-C: Asymptotically strict pseudocontractive mappings in the intermediate sense. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(10):3502–3511. 10.1016/j.na.2008.07.007
Ceng LC, Petrusel A, Yao JC: A hybrid method for Lipschitz continuous monotone mappings and asymptotically strict pseudocontractive mappings in the intermediate sense. to appear in Journal of Nonlinear and Convex Analysis
Ceng LC, Petrusel A, Yao JC: Iterative approximation of fixed points for asymptotically strict pseudocontractive type mappings in the intermediate sense. to appear in Taiwanese Journal of Mathematics
Ceng LC, Sahu DR, Yao JC: Implicit iterative algorithms for asymptotically nonexpansive mappings nonexpansive mappings in the intermediate sense and Lipschitz-continuous monotone mappings. to appear in Journal of Computational and Applied Mathematics
Chang S-S, Lee HWJ, Chan CK: A new method for solving equilibrium problem fixed point problem and variational inequality problem with application to optimization. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(9):3307–3319. 10.1016/j.na.2008.04.035
Cioranescu I: Geometry of Banach Spaces, Duality Mappings and Nonlinear Problems, Mathematics and Its Applications. Volume 62. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1990:xiv+260.
Alber YI: Metric and generalized projection operators in Banach spaces: properties and applications. In Theory and Applications of Nonlinear Operators of Accretive and Monotone Type, Lecture Notes in Pure and Applied Mathematics. Volume 178. Edited by: Kartosator AG. Dekker, New York, NY, USA; 1996:15–50.
Chang SS: On the generalized mixed equilibrium problem in Banach spaces. Journal of Applied Mathematics and Mechanics 2009, 30(9):1105–1112. 10.1007/s10483-009-0904-6
Acknowledgment
This work was supported by the Natural Science Foundation of Yibin University (no. 2009Z3) and the Kyungnam University Research Fund 2009.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chang, Ss., Kim, J. & Wang, X. Modified Block Iterative Algorithm for Solving Convex Feasibility Problems in Banach Spaces. J Inequal Appl 2010, 869684 (2010). https://doi.org/10.1155/2010/869684
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/869684
 is a uniformly smooth Banach space, then
is a uniformly smooth Banach space, then 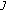 is uniformly continuous on each bounded subset of
is uniformly continuous on each bounded subset of 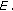
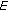 is a reflexive and strictly convex Banach space, then
is a reflexive and strictly convex Banach space, then 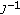 is hemicontinuous, that is,
is hemicontinuous, that is, 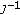 is norm-
is norm- -continuous.
-continuous. is a smooth, strictly convex, and reflexive Banach space, then the normalized duality mapping
is a smooth, strictly convex, and reflexive Banach space, then the normalized duality mapping  is single-valued, one-to-one, and onto.
is single-valued, one-to-one, and onto.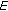 is uniformly smooth if and only if
is uniformly smooth if and only if 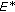 is uniformly convex.
is uniformly convex.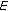 has the Kadec-Klee property, that is, for any sequence
has the Kadec-Klee property, that is, for any sequence 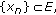 if
if 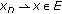 and
and 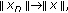 then
then 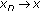 .
.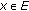 and
and 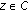 , then
, then 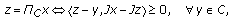
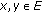 ,
, 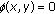 if and only if
if and only if 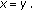
 -nonexpansive mapping to an infinite family of quasi-
-nonexpansive mapping to an infinite family of quasi- -asymptotically mappings;
-asymptotically mappings;