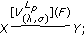- Research Article
- Open access
- Published:
On Asymptotically  -Statistical Equivalent Sequences of Fuzzy Numbers
-Statistical Equivalent Sequences of Fuzzy Numbers
Journal of Inequalities and Applications volume 2010, Article number: 838741 (2010)
Abstract
The goal of this paper is to give the asymptotically  -statistical equivalent which is a natural combination of the definition for asymptotically equivalent, invariant mean and
-statistical equivalent which is a natural combination of the definition for asymptotically equivalent, invariant mean and  -statistical convergence of fuzzy numbers.
-statistical convergence of fuzzy numbers.
1. Introduction
The concepts of fuzzy sets and fuzzy set operation were first introduced by Zadeh [1] and subsequently several authors have discussed various aspects of the theory and applications of fuzzy sets such as fuzzy topological spaces similarity relations and fuzzy orderings, fuzzy measures of fuzzy events and fuzzy mathematical programming. Matloka [2] introduced bounded and convergent sequences of fuzzy numbers and studied their some properties. For sequences of fuzzy numbers, Nuray and Savaş [3] introduced and discussed the concepts of statistically convergent and statistically Cauchy sequences.
Quite recently, Savaş [4] introduced the idea of asymptotically  -statistically equivalent sequences of fuzzy numbers. In this paper we extend his result by using invariant means.
-statistically equivalent sequences of fuzzy numbers. In this paper we extend his result by using invariant means.
2. Preliminaries
Before we enter the motivation for this paper and presentation of the main results we give some preliminaries.
By  and
and  , we denote the Banach spaces of bounded and convergent sequences
, we denote the Banach spaces of bounded and convergent sequences  normed by
normed by  , respectively. A linear functional
, respectively. A linear functional  on
on  is said to be a Banach limit (see [5]) if it has the following properties:
is said to be a Banach limit (see [5]) if it has the following properties:
(1) if
if  for all
for all  ;
;
(2) where
where  ;
;
(3) , where the shift operator
, where the shift operator  is defined by
is defined by  .
.
Let  be the set of all Banach limits on
be the set of all Banach limits on  . A sequence
. A sequence  is said to be almost convergent if all Banach limits of
is said to be almost convergent if all Banach limits of  coincide. Let
coincide. Let  denote the space of almost convergent sequences.
denote the space of almost convergent sequences.
Let  be a one-to-one mapping from the set of natural numbers into itself. A continuous linear functional
be a one-to-one mapping from the set of natural numbers into itself. A continuous linear functional  on
on  is said to be an invariant mean or a
is said to be an invariant mean or a  -mean if and only if
-mean if and only if
(1) when the sequence
when the sequence  is such that
is such that  for all
for all  ,
,
(2) where
where  , and
, and
(3) for all
for all  .
.
Throughout this paper we shall consider the mapping  has having on finite orbits, that is,
has having on finite orbits, that is,  for all nonnegative integers with
for all nonnegative integers with  , where
, where  is the
is the  th iterate of
th iterate of  at
at  . Thus
. Thus  -mean extends the limit functional on
-mean extends the limit functional on  in the sense that
in the sense that  for all
for all  . Consequently,
. Consequently,  where
where  is the set of bounded sequences all of whose
is the set of bounded sequences all of whose  -mean are equal.
-mean are equal.
In the case when  , the
, the  -mean is often called the Banach limit and
-mean is often called the Banach limit and  is the set of almost convergent sequences.
is the set of almost convergent sequences.
A fuzzy real number  is a fuzzy set on
is a fuzzy set on  , that is, a mapping
, that is, a mapping  associating each real number
associating each real number  with its grade of membership
with its grade of membership  .
.
The  cut of fuzzy real number
cut of fuzzy real number  is denoted by
is denoted by  , where
, where  . If
. If  then it is the closure of the strong
then it is the closure of the strong  . A fuzzy real number
. A fuzzy real number  is said to be upper semicontinuous if for each
is said to be upper semicontinuous if for each  ,
,  , for all
, for all  is open in the usual topology of
is open in the usual topology of  . If there exists
. If there exists  such that
such that  , then the fuzzy real number
, then the fuzzy real number  is called normal.
is called normal.
A fuzzy number  is said to be convex, if
is said to be convex, if  where
where  . The class of all upper semi-continuous, normal, convex fuzzy real numbers is denoted by
. The class of all upper semi-continuous, normal, convex fuzzy real numbers is denoted by  and throughout the article, by a fuzzy real number we mean that the number belongs to
and throughout the article, by a fuzzy real number we mean that the number belongs to  . Let
. Let  and the
and the  level sets be
level sets be

Then the arithmetic operations on  are defined as follows:
are defined as follows:

The above operations can be defined in terms of  level sets as follows:
level sets as follows:

The additive identity and multiplicative identity in  are denoted by
are denoted by  and
and  , respectively.
, respectively.
Let  the set of all closed and bounded intervals
the set of all closed and bounded intervals  Then we write
Then we write  , if and only if
, if and only if  and
and  , and
, and

It is obvious that  is a complete metric space. Now we define the metric
is a complete metric space. Now we define the metric  by
by

for 
We now give the following definitions (see [6]) for fuzzy real-valued sequences.
Definition 2.1.
A fuzzy real-valued sequence  is a function
is a function  from the set
from the set  of natural numbers into
of natural numbers into  ). The fuzzy real-valued sequence
). The fuzzy real-valued sequence  denotes the value of the function at
denotes the value of the function at  and is called the
and is called the  th term of the sequence. We denote by
th term of the sequence. We denote by  the set of all fuzzy real-valued sequences
the set of all fuzzy real-valued sequences  .
.
Definition 2.2.
A fuzzy real-valued sequence  is said to be convergent to a fuzzy number
is said to be convergent to a fuzzy number  written as
written as  , if for every
, if for every  there exists a positive integer
there exists a positive integer  such that
such that

Let  denote the set of all convergent sequences of fuzzy numbers.
denote the set of all convergent sequences of fuzzy numbers.
Definition 2.3.
A sequence  of fuzzy numbers is said to be bounded if the set
of fuzzy numbers is said to be bounded if the set  of fuzzy numbers is bounded. We denote by
of fuzzy numbers is bounded. We denote by  the set of all bounded sequences of fuzzy numbers.
the set of all bounded sequences of fuzzy numbers.
It is easy to see that

It was shown that  and
and  are complete metric spaces (see [7]).
are complete metric spaces (see [7]).
3. Definitions and Notations
Definition 3.1.
Two fuzzy real-valued sequences  and
and  are said to be asymptotically equivalent if
are said to be asymptotically equivalent if

(denoted by  ).
).
Let  be a nondecreasing sequence of positive reals tending to infinity and
be a nondecreasing sequence of positive reals tending to infinity and  and
and  .
.
In [4], Savaş introduced the concept of  -statistical convergence of fuzzy numbers as follows.
-statistical convergence of fuzzy numbers as follows.
Definition 3.2.
A fuzzy real-valued sequences  is said to be
is said to be  -statistically convergent or
-statistically convergent or  -convergent to L if for every
-convergent to L if for every  ,
,

In this case we write  or
or  , and
, and

The next definition is natural combination of Definitions 3.1 and 3.2., which was defined in [4].
Definition 3.3.
Two fuzzy real-valued sequences  and
and  are said to be asymptotically
are said to be asymptotically  -statistical equivalent of multiple
-statistical equivalent of multiple  provided that for every
provided that for every 

(denoted by  ) and simply asymptotically
) and simply asymptotically  -statistical equivalent if
-statistical equivalent if  .
.
If we take  , the above definition reduces to the following definition.
, the above definition reduces to the following definition.
Definition 3.4.
Two fuzzy real-valued sequences  and
and  are said to be asymptotically statistical equivalent of multiple
are said to be asymptotically statistical equivalent of multiple  provided that for every
provided that for every  ,
,

(denoted by  ) and simply asymptotically statistical equivalent if
) and simply asymptotically statistical equivalent if  .
.
It is quite naturel to expect the following definition.
Definition 3.5.
Fuzzy real-valued sequences  is said to be
is said to be  -statistically convergent to
-statistically convergent to  provided that for every
provided that for every 

uniformly in  .
.
In this case we write  or
or  , and
, and

Following this result we introduce two new notions asymptotically  -statistical equivalent of multiple
-statistical equivalent of multiple  and strong
and strong  -asymptotically equivalent of multiple
-asymptotically equivalent of multiple  .
.
Definition 3.6.
Two fuzzy real-valued sequences  and
and  are said to be asymptotically
are said to be asymptotically  -statistical equivalent of multiple
-statistical equivalent of multiple  provided that for every
provided that for every 

uniformly in  , (denoted by
, (denoted by  ) and simply asymptotically
) and simply asymptotically  -statistical equivalent if
-statistical equivalent if  .
.
In case  , the above definition reduces to the following definition.
, the above definition reduces to the following definition.
Definition 3.7.
Two fuzzy real-valued sequences  and
and  are said to be asymptotically
are said to be asymptotically  -statistical equivalent of multiple
-statistical equivalent of multiple  provided that for every
provided that for every 

uniformly in  , (denoted by
, (denoted by  ) and simply asymptotically
) and simply asymptotically  -statistical equivalent if
-statistical equivalent if  .
.
We now define the following.
Definition 3.8.
Let  be a sequence of positive real numbers; two fuzzy real-valued sequences
be a sequence of positive real numbers; two fuzzy real-valued sequences  and
and  are strongly asymptotically
are strongly asymptotically  -equivalent of multiple
-equivalent of multiple  , provided that
, provided that

(denoted by  ) and simply strongly asymptotically
) and simply strongly asymptotically  -equivalent if
-equivalent if  .
.
If we take  for all
for all  we write
we write  instead of (
instead of ( ).
).
In case  in above definition we get following.
in above definition we get following.
Definition 3.9.
Let  be a sequence of positive numbers and let us consider two fuzzy real-valued sequences
be a sequence of positive numbers and let us consider two fuzzy real-valued sequences  and
and  . Two fuzzy real-valued sequences
. Two fuzzy real-valued sequences  and
and  are said to be strongly asymptotically Cesáro equivalent of multiple
are said to be strongly asymptotically Cesáro equivalent of multiple  provided that
provided that

(denoted by  ), and simply strong Cesáro asymptotically equivalent if
), and simply strong Cesáro asymptotically equivalent if  .
.
4. Main Results
Theorem 4.1.
Let  . Then
. Then
-
(1)
if
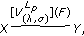 then
then 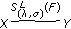 ;
; -
(2)
if
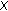 and
and 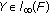 and
and  then
then 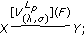
(3)
Proof.
Part (1): if  and
and  then
then

Therefore  . Part (2): suppose that fuzzy real-valued sequences
. Part (2): suppose that fuzzy real-valued sequences  and
and  are in
are in  and
and  . Then we can assume that
. Then we can assume that  . Let
. Let  be given and
be given and  be such that
be such that

for all  and let
and let

Now for all  we have
we have

Hence  . This completes the proof.Part (3): this immediately follows from (1) and (2).
. This completes the proof.Part (3): this immediately follows from (1) and (2).
In the next theorem we prove the following relation.
Theorem 4.2.
Let  . Then
. Then  implies
implies 
Proof.
Let  and
and  be given. Then
be given. Then

Hence  .
.
Theorem 4.3.
Let fuzzy real-valued sequences  and
and  be bounded and
be bounded and  . Then
. Then  implies
implies  .
.
Proof.
Suppose that fuzzy real-valued sequences  and
and  be bounded and
be bounded and  is given. Since
is given. Since  and
and  are bounded there exists an integer
are bounded there exists an integer  such that
such that  for all
for all  and
and  ; then
; then

Hence  .
.
Remark 4.4.
If we take  in our results, all results reduce to the results of almost convergence which have not proved so far.
in our results, all results reduce to the results of almost convergence which have not proved so far.
References
Zadeh LA: Fuzzy sets. Information and Computation 1965, 8: 338–353.
Matloka M: Sequences of fuzzy numbers. BUSEFAL 1986, 28: 28–37.
Nuray F, Savaş E: Statistical convergence of sequences of fuzzy numbers. Mathematica Slovaca 1995, 45(3):269–273.
Savaş E: On asymptotically -statistical equivalent sequences of fuzzy numbers. New Mathematics & Natural Computation 2007, 3(3):301–306. 10.1142/S1793005707000781
Banach S: Theorie des Operations Linearies. Subwncji Funduszu Narodowej, Warszawa, Poland; 1932.
Savas E: On asymptotically lacunary -statistical equivalent sequences of Fuzzy numbers,. New Mathematics & Natural Computation 2009, 5(3):1–10.
Nanda S: On sequences of fuzzy numbers. Fuzzy Sets and Systems 1989, 33(1):123–126. 10.1016/0165-0114(89)90222-4
Acknowledgment
This work was supported by Grant (2008-FED-B162) of Yüzüncü Yil university.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Savaş, E., Şevli, H. & Cancan, M. On Asymptotically  -Statistical Equivalent Sequences of Fuzzy Numbers.
J Inequal Appl 2010, 838741 (2010). https://doi.org/10.1155/2010/838741
-Statistical Equivalent Sequences of Fuzzy Numbers.
J Inequal Appl 2010, 838741 (2010). https://doi.org/10.1155/2010/838741
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/838741
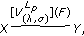 then
then 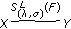 ;
;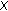 and
and 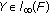 and
and  then
then