- Research Article
- Open access
- Published:
On Boundedness of Weighted Hardy Operator in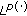 
and Regularity Condition
Journal of Inequalities and Applications volume 2010, Article number: 837951 (2010)
Abstract
We give a new proof for power-type weighted Hardy inequality in the norms of generalized Lebesgue spaces 
. Assuming the logarithmic conditions of regularity in a neighborhood of zero and at infinity for the exponents 
, necessary and sufficient conditions are proved for the boundedness of the Hardy operator 
from 
into 
. Also a separate statement on the exactness of logarithmic conditions at zero and at infinity is given. This shows that logarithmic regularity conditions for the functions 
at the origin and infinity are essentially one.
Publisher note
To access the full article, please see PDF.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Harman, A., Mamedov, F. On Boundedness of Weighted Hardy Operator in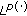 
and Regularity Condition.
J Inequal Appl 2010, 837951 (2010). https://doi.org/10.1155/2010/837951
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/837951