- Research Article
- Open access
- Published:
Derivatives of Orthonormal Polynomials and Coefficients of Hermite-Fejér Interpolation Polynomials with Exponential-Type Weights
Journal of Inequalities and Applications volume 2010, Article number: 816363 (2010)
Abstract
Let  , and let
, and let  be an even function. In this paper, we consider the exponential-type weights
be an even function. In this paper, we consider the exponential-type weights  , and the orthonormal polynomials
, and the orthonormal polynomials  of degree
of degree  with respect to
with respect to  . So, we obtain a certain differential equation of higher order with respect to
. So, we obtain a certain differential equation of higher order with respect to  and we estimate the higher-order derivatives of
and we estimate the higher-order derivatives of  and the coefficients of the higher-order Hermite-Fejér interpolation polynomial based at the zeros of
and the coefficients of the higher-order Hermite-Fejér interpolation polynomial based at the zeros of  .
.
1. Introduction
Let  and
and  . Let
. Let  be an even function and let
be an even function and let  be such that
be such that  for all
for all  For
For  , we set
, we set

Then we can construct the orthonormal polynomials  of degree
of degree  with respect to
with respect to  . That is,
. That is,

We denote the zeros of  by
by

A function  is said to be quasi-increasing if there exists
is said to be quasi-increasing if there exists  such that
such that  for
for  . For any two sequences
. For any two sequences  and
and  of nonzero real numbers (or functions), we write
of nonzero real numbers (or functions), we write  if there exists a constant
if there exists a constant  independent of
independent of  (or
(or  ) such that
) such that  for
for  being large enough. We write
being large enough. We write  if
if  and
and  . We denote the class of polynomials of degree at most
. We denote the class of polynomials of degree at most  by
by  .
.
Throughout  denote positive constants independent of
denote positive constants independent of  , and polynomials of degree at most
, and polynomials of degree at most  . The same symbol does not necessarily denote the same constant in different occurrences.
. The same symbol does not necessarily denote the same constant in different occurrences.
We shall be interested in the following subclass of weights from [1].
Definition 1.1.
Let  be even and satisfy the following properties.
be even and satisfy the following properties.
(a) is continuous in
is continuous in  , with
, with  .
.
(b) exists and is positive in
exists and is positive in  .
.
(c)One has

(d)The function

is quasi-increasing in  with
with

(e)There exists  such that
such that

Then we write  . If there also exist a compact subinterval
. If there also exist a compact subinterval  of
of  and
and  such that
such that

then we write  .
.
In the following we introduce useful notations.
(a)Mhaskar-Rahmanov-Saff (MRS) numbers  is defined as the positive roots of the following equations:
is defined as the positive roots of the following equations:

(b)Let

(c)The function  is defined as the following:
is defined as the following:

In [2, 3] we estimated the orthonormal polynomials  associated with the weight
associated with the weight  and obtained some results with respect to the derivatives of orthonormal polynomials
and obtained some results with respect to the derivatives of orthonormal polynomials  . In this paper, we will obtain the higher derivatives of
. In this paper, we will obtain the higher derivatives of  . To estimate of the higher derivatives of the orthonormal polynomials sequence, we need further assumptions for
. To estimate of the higher derivatives of the orthonormal polynomials sequence, we need further assumptions for  as follows.
as follows.
Definition 1.2.
Let  and let
and let  be a positive integer. Assume that
be a positive integer. Assume that  is
is  -times continuously differentiable on
-times continuously differentiable on  and satisfies the followings.
and satisfies the followings.
(a) exists and
exists and  ,
,  are positive for
are positive for  .
.
(b)There exist positive constants  such that for
such that for 

(c)There exist constants  and
and  such that on
such that on 

Then we write  . Furthermore,
. Furthermore,  and
and  satisfies one of the following.
satisfies one of the following.
(a) is quasi-increasing on a certain positive interval
is quasi-increasing on a certain positive interval  .
.
(b) is nondecreasing on a certain positive interval
is nondecreasing on a certain positive interval  .
.
(c)There exists a constant  such that
such that  on
on  .
.
Then we write  .
.
Now, consider some typical examples of  . Define for
. Define for  and
and  ,
,

More precisely, define for  ,
,  ,
,  and
and  ,
,

where  if
if  , otherwise
, otherwise  , and define
, and define

In the following, we consider the exponential weights with the exponents  . Then we have the following examples (see [4]).
. Then we have the following examples (see [4]).
Example 1.3.
Let  be a positive integer. Let
be a positive integer. Let  . Then one has the following.
. Then one has the following.
(a) belongs to
belongs to  .
.
(b)If  and
and  , then there exists a constant
, then there exists a constant  such that
such that  is quasi-increasing on
is quasi-increasing on  .
.
(c)When  , if
, if  , then there exists a constant
, then there exists a constant  such that
such that  is quasi-increasing on
is quasi-increasing on  , and if
, and if  , then
, then  is quasidecreasing on
is quasidecreasing on  .
.
(d)When  and
and  ,
,  is nondecreasing on a certain positive interval
is nondecreasing on a certain positive interval  .
.
In this paper, we will consider the orthonormal polynomials  with respect to the weight class
with respect to the weight class  . Our main themes in this paper are to obtain a certain differential equation for
. Our main themes in this paper are to obtain a certain differential equation for  of higher-order and to estimate the higher-order derivatives of
of higher-order and to estimate the higher-order derivatives of  at the zeros of
at the zeros of  and the coefficients of the higher-order Hermite-Fejér interpolation polynomials based at the zeros of
and the coefficients of the higher-order Hermite-Fejér interpolation polynomials based at the zeros of  . More precisely, we will estimate the higher-order derivatives of
. More precisely, we will estimate the higher-order derivatives of  at the zeros of
at the zeros of  for two cases of an odd order and of an even order. These estimations will play an important role in investigating convergence or divergence of higher-order Hermite-Fejér interpolation polynomials (see [5–16]).
for two cases of an odd order and of an even order. These estimations will play an important role in investigating convergence or divergence of higher-order Hermite-Fejér interpolation polynomials (see [5–16]).
This paper is organized as follows. In Section 2, we will obtain the differential equations for  of higher-order. In Section 3, we will give estimations of higher-order derivatives of
of higher-order. In Section 3, we will give estimations of higher-order derivatives of  at the zeros of
at the zeros of  in a certain finite interval for two cases of an odd order and of an even order. In addition, we estimate the higher-order derivatives of
in a certain finite interval for two cases of an odd order and of an even order. In addition, we estimate the higher-order derivatives of  at all zeros of
at all zeros of  for two cases of an odd order and of an even order. Furthermore, we will estimate the coefficients of higher-order Hermite-Fejér interpolation polynomials based at the zeros of
for two cases of an odd order and of an even order. Furthermore, we will estimate the coefficients of higher-order Hermite-Fejér interpolation polynomials based at the zeros of  , in Section 4.
, in Section 4.
2. Higher-Order Differential Equation for Orthonormal Polynomials
In the rest of this paper we often denote  and
and  simply by
simply by  and
and  , respectively. Let
, respectively. Let  if
if  is odd,
is odd,  otherwise, and define the integrating functions
otherwise, and define the integrating functions  and
and  with respect to
with respect to  as follows:
as follows:

where  and
and  . Then in [3, Theorem
. Then in [3, Theorem  ] we have a relation of the orthonormal polynomial
] we have a relation of the orthonormal polynomial  with respect to the weight
with respect to the weight  :
:

Theorem 2.1 (cf. [6, Theorem  ]).
]).
Let  and
and  . Then for
. Then for  one has the second-order differential relation as follows:
one has the second-order differential relation as follows:

Here, one knows that for any integer  ,
,

where

Especially, when  is odd, one has
is odd, one has

where  is the polynomial of degree
is the polynomial of degree  with
with  .
.
Proof.
We may similarly repeat the calculation [6, Proof of Theorem  ], and then we obtain the results. We stand for
], and then we obtain the results. We stand for  simply. Applying (2.2) to
simply. Applying (2.2) to  we also see
we also see

and so if we use the recurrence formula

and use (2.2) too, then we obtain the following:

We differentiate the left and right sides of (2.2) and substitute (2.2) and (2.9). Then consequently, we have, for  ,
,

Using the recurrence formula (2.8) and  , we have
, we have

because  is an odd function. Therefore, we have
is an odd function. Therefore, we have

When  is odd, since
is odd, since  , (2.6) is proved.
, (2.6) is proved.
For the higher-order differential equation for orthonormal polynomials, we see that for  and
and 

Let  for nonnegative integer
for nonnegative integer  . In the following theorem, we show the higher-order differential equation for orthonormal polynomials.
. In the following theorem, we show the higher-order differential equation for orthonormal polynomials.
Theorem 2.2.
Let  and
and  . Let
. Let  and
and  . Then one has the following equation for
. Then one has the following equation for  :
:

where

and for  and
and 

and for 

Proof.
It comes from Theorem 2.1 and (2.13).
Corollary 2.3.
Under the same assumptions as Theorem 2.1, if  is odd, then
is odd, then

where  and for
and for 

Proof.
Let  be odd. Then we will consider (2.6). Since
be odd. Then we will consider (2.6). Since  , we have
, we have

and we have

Therefore, we have the result from (2.6).
In the rest of this paper, we let  and
and  for positive integer
for positive integer  and assume that
and assume that  for
for  and
and

where  is defined in (1.13).
is defined in (1.13).
In Section 3, we will estimate the higher-order derivatives of orthonormal polynomials at the zeros of orthonormal polynomials with respect to exponential-type weights.
3. Estimation of Higher-Order Derivatives of Orthonormal Polynomials
From [3, Theorem  ] we know that there exist
] we know that there exist  and
and  such that for
such that for  and
and  ,
,

If  is unbounded, then (2.22) is trivially satisfied. Additionally we have, from [17, Theorem
is unbounded, then (2.22) is trivially satisfied. Additionally we have, from [17, Theorem  ], that if we assume that
], that if we assume that  is nondecreasing, then for
is nondecreasing, then for  with
with 

where there exists a constant  such that
such that


Here,  and
and  for some
for some  .
.
For the higher derivatives of  and
and  , we have the following results in [17, Theorem
, we have the following results in [17, Theorem  ].
].
Theorem 3.1 (see[17, Theorem  ]).
]).
For  and
and 

Moreover, there exists  such that for
such that for  and
and  ,
,

with  as
as  .
.
Corollary 3.2.
Let  . Then there exists a positive constant
. Then there exists a positive constant  such that one has for
such that one has for  and
and  ,
,

In the following, we have the estimation of the higher-order derivatives of orthonormal polynomials.
Theorem 3.3.
Let  and
and  . Then for
. Then for  the following equality holds for
the following equality holds for  large enough:
large enough:

where

and  . Moreover, for
. Moreover, for 

Here,

Corollary 3.4.
Suppose the same assumptions as Theorem 3.3. Given any  , there exists a small fixed positive constant
, there exists a small fixed positive constant  such that (3.8) holds satisfying
such that (3.8) holds satisfying  and
and

for  .
.
Corollary 3.5.
For  and
and 

Theorem 3.6.
Let  and let
and let  ,
,  . Then
. Then

and especially if  is even, then
is even, then

We note that for  large enough,
large enough,

because we know that  from [3, Theorem
from [3, Theorem  ] and
] and

To prove these results we need some lemmas.
Lemma 3.7.
-
(a)
For
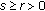
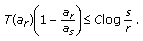 (3.18)
(3.18)
(b) For 

(c) For 

(d) Let  . Then for
. Then for 

and for 

Proof.
-
(a)
It is [1, Lemma
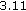 (c)]. (b) It is [1, Lemma
(c)]. (b) It is [1, Lemma 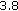 (c)]. (c) It comes from (3.1). (d) Since
(c)]. (c) It comes from (3.1). (d) Since 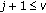 ,
, 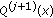 is increasing. So, we obtain (d) by (1.12).
is increasing. So, we obtain (d) by (1.12).
Lemma 3.8.
Let  , and
, and  ,
,  , be defined in Theorem 2.1.
, be defined in Theorem 2.1.
-
(a)
For
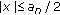 and
and 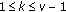 , there exists
, there exists 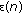 satisfying
satisfying  as
as 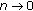 such that
such that

Moreover, for  and
and  ,
,

(b) For  and
and  , there exists
, there exists  satisfying
satisfying  as
as  such that
such that

Moreover, for  and
and  ,
,

(c) For  and
and  , there exists
, there exists  satisfying
satisfying  as
as  such that
such that

Moreover, for  and
and  ,
,

(d) For  and
and  , there exists
, there exists  satisfying
satisfying  as
as  such that
such that

Moreover, for  and
and  ,
,

Proof.
-
(a)
Since
 , we prove it by Theorem 3.1.
, we prove it by Theorem 3.1.
(b) For  , we see
, we see

From (3.18), we know that  . Therefore by (3.19), (3.21), and (3.6) we have for
. Therefore by (3.19), (3.21), and (3.6) we have for 

and for  we have by (3.21) and (3.22)
we have by (3.21) and (3.22)

Consequently we have (b).
(c) Next we estimate  . Suppose
. Suppose  . Let us set
. Let us set  . By (3.6) and (3.20) we have
. By (3.6) and (3.20) we have

For  , we obtain the same estimate as
, we obtain the same estimate as 

For  , we have similarly to the case of
, we have similarly to the case of 

(d) It is similar to (c). Consequently we have the following lemma.
Lemma 3.9.
Let  ,
,  , and
, and  . Let
. Let  . Then
. Then

where  is defined in Theorem 3.3 and for
is defined in Theorem 3.3 and for 

Moreover, for  ,
,

Proof.
Since

we have (3.39) for  by (3.5). For
by (3.5). For  we have from (3.6) and (3.19) that
we have from (3.6) and (3.19) that

Moreover, we can obtain (3.38) for  from the above easily.
from the above easily.
Lemma 3.10.
Let  and
and  . Let
. Let  . Then for
. Then for 

with  , where
, where  ,
,  , and
, and  are defined in Theorem 3.3. For
are defined in Theorem 3.3. For  one has
one has

On the other hand, one has for  ,
,

Proof.
First, we know that

Suppose  . Since from (3.18) and (3.19)
. Since from (3.18) and (3.19)

we have from (3.6)

Since

we know from (3.6) that

Therefore we have for 

Since from (3.3)

and similarly

we have

Then we have

Therefore, since

there exist constants  with
with  such that we have for
such that we have for 

Especially, from the above estimates we can see (3.43) for  . On the other hand, suppose
. On the other hand, suppose  . Then since from Theorem 2.1 and (3.5)
. Then since from Theorem 2.1 and (3.5)

and  , we have from Lemma 3.8
, we have from Lemma 3.8

Therefore, we have (3.44) for  .
.
Lemma 3.11.
Let  and
and  . Let
. Let  . Then for
. Then for  , there exists
, there exists  satisfying
satisfying  as
as  such that
such that

Moreover, one has for  ,
,

Proof.
For  we have from Lemma 3.8 that there exists
we have from Lemma 3.8 that there exists  satisfying
satisfying  as
as  such that
such that

Similarly, for  and
and  ,
,

Therefore, we have the results.
Proof of Theorem 3.3.
First we know that the following differential equation is satisfied:

Suppose  . Then since we see from (3.63) and (3.38) that
. Then since we see from (3.63) and (3.38) that

we have by (3.63) and mathematical induction

Next, suppose  . More precisely, from Lemma 3.9 we have
. More precisely, from Lemma 3.9 we have

Then by (3.63), (3.42), and (3.66) there exists a constant  with
with

such that we have that

Suppose that there exist constants  with
with  such that
such that


Then we have by (3.38) and (3.70)

and we have by (3.42) and (3.69)

where  and
and  . Also, we have by (3.59) that for
. Also, we have by (3.59) that for 

Therefore, there exists  satisfying
satisfying  such that
such that

Moreover, we have by (3.37) and (3.65)

and by (3.43) and (3.70)

Also we obtain by (3.59) and (3.65) that for 

Therefore, since we have by (3.63) that

we proved the results.
Proof.
From (3.3), Theorem 3.1, and the definitions of  in Theorem 3.3, if for any
in Theorem 3.3, if for any  we choose a fixed constant
we choose a fixed constant  small enough, then there exists an integer
small enough, then there exists an integer  such that we can make
such that we can make  ,
,  , and
, and  small enough for
small enough for  with
with  .
.
Proof of Corollary 3.5.
Since we have from Lemma 3.8 that  ,
,  for
for  and
and  for
for  , we obtain using the mathematical induction that
, we obtain using the mathematical induction that

Therefore, from (3.65) we prove the result easily.
Proof of Theorem 3.6.
We know that from (3.39)

and from (3.44)

Suppose

Then since

we have

Here, we used that  . Similarly, since
. Similarly, since

we have

4. Estimation of the Coefficients of Higher-Order Hermite-Fejér Interpolation
Let  be nonnegative integers with
be nonnegative integers with  . For
. For  we define the
we define the  -order Hermite-Fejér interpolation polynomials
-order Hermite-Fejér interpolation polynomials  as follows: for each
as follows: for each  ,
,

Especially for each  we see
we see  . The fundamental polynomials
. The fundamental polynomials  ,
,  of
of  are defined by
are defined by

Here,  is fundamental Lagrange interpolation polynomial of degree
is fundamental Lagrange interpolation polynomial of degree  (cf. [18, page 23]) given by
(cf. [18, page 23]) given by

and  satisfies
satisfies

Then

In this section, we often denote  and
and  if it does not confuse us. Then we will first estimate
if it does not confuse us. Then we will first estimate  for
for  . Since we have
. Since we have

by induction on  , we can estimate
, we can estimate  .
.
Theorem 4.1.
Let  . Then one has for
. Then one has for 

In addition, one has that for 

and if  is odd, then one has that for
is odd, then one has that for 

For  define
define  and for
and for 

Theorem 4.2 (cf. [10, Lemma  ]).
]).
Let  and let
and let  . Then for
. Then for  there exists uniquely a sequence
there exists uniquely a sequence  of positive numbers
of positive numbers

and  . Moreover, one has for
. Moreover, one has for 

Theorem 4.3.
Suppose the same assumptions as Theorem 4.2. Given any  , there exists a small fixed positive constant
, there exists a small fixed positive constant  such that (4.11) holds satisfying
such that (4.11) holds satisfying  and
and

for  .
.
Theorem 4.4.
Let  . Then one has for
. Then one has for 

On the other hand, one has for 

Especially, if  is odd, then one has
is odd, then one has

Especially, for  we define the
we define the  -order Hermite-Fejér interpolation polynomials
-order Hermite-Fejér interpolation polynomials  as the
as the  -order Hermite-Fejér interpolation polynomials
-order Hermite-Fejér interpolation polynomials  . Then we know that
. Then we know that

where  and
and

Then for the convergence theorem with respect to  we have the following corollary.
we have the following corollary.
Corollary 4.5.
Let  . Then one has for
. Then one has for 

On the other hand, one has for 

Especially, if  is odd, then one has
is odd, then one has

Proof of Theorem 4.1.
Theorem 4.1 is shown by induction with respect to  . The case of
. The case of  follows from (4.6), Corollary 3.5, and Theorem 3.6. Suppose that for the case of
follows from (4.6), Corollary 3.5, and Theorem 3.6. Suppose that for the case of  the results hold. Then from the following relation:
the results hold. Then from the following relation:

we have (4.7) and (4.8). Moreover, we obtain (4.9) from the following: for 

Proof of Theorem 4.2.
Similarly to Theorem 4.1, we use mathematical induction with respect to  . From Theorem 3.3 we know that for
. From Theorem 3.3 we know that for 

and for 

where  and
and

Then from the following relations:

we have the results by induction with respect to  .
.
Proof of Theorem 4.3.
It is proved by the same reason as the proof of Corollary 3.4.
Proof of Theorem 4.4.
To prove the result, we proceed by induction on  . From (4.2) and (4.4) we know that
. From (4.2) and (4.4) we know that  and the following recurrence relation; for
and the following recurrence relation; for 

When  ,
,  so that (4.14) and (4.15) are satisfied for
so that (4.14) and (4.15) are satisfied for  . From (4.7), (4.8), (4.28), and assumption of induction on
. From (4.7), (4.8), (4.28), and assumption of induction on  , for
, for  , we have the results easily. When
, we have the results easily. When  is odd, we know that
is odd, we know that

Therefore, similarly we have (4.16) from (4.8), (4.9), (4.28), and assumption of induction on  .
.
Proof of Corollary 4.5.
Since  , it is trivial from Theorem 4.4.
, it is trivial from Theorem 4.4.
We rewrite the relation (4.10) in the form for  ,
,

and for  ,
,

Now, for every  we will introduce an auxiliary polynomial determined by
we will introduce an auxiliary polynomial determined by  as the following lemma.
as the following lemma.
Lemma 4.6 (see[10, Lemma  ]).
]).
-
(i)
For
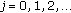 , there exists a unique polynomial
, there exists a unique polynomial 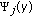 of degree
of degree  such that
such that 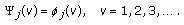 (4.32)
(4.32)
(ii) and
and  ,
,  .
.
Since  is a polynomial of degree
is a polynomial of degree  , we can replace
, we can replace  in (4.10) with
in (4.10) with  , that is,
, that is,

for an arbitrary  and
and  . We use the notation
. We use the notation  which coincides with
which coincides with  if
if  is an integer. Since
is an integer. Since  , we have
, we have  for
for  in a neighborhood of
in a neighborhood of  and an arbitrary real number
and an arbitrary real number  .
.
We can show that  is a polynomial of degree at most
is a polynomial of degree at most  with respect to
with respect to  for
for  , where
, where  is the
is the  th partial derivative of
th partial derivative of  with respect to
with respect to  at
at  (see [6, page 199]). We prove these facts by induction on
(see [6, page 199]). We prove these facts by induction on  . For
. For  it is trivial. Suppose that it holds for
it is trivial. Suppose that it holds for  . To simplify the notation, let
. To simplify the notation, let  and
and  for a fixed
for a fixed  . Then
. Then  . By Leibniz's rule, we easily see that
. By Leibniz's rule, we easily see that

which shows that  is a polynomial of degree at most
is a polynomial of degree at most  with respect to
with respect to  . Let
. Let  ,
,  be defined by
be defined by

Then  is a polynomial of degree at most
is a polynomial of degree at most  .
.
By Theorem 4.2 we have the following.
Lemma 4.7 (see[10, Lemma  ]).
]).
Let  , and let
, and let  be a positive constant. If
be a positive constant. If  and
and  , then
, then


Lemma 4.8 (see[10, Lemma  ]).
]).
If  , then for
, then for  ,
,

Lemma 4.9.
For positive integers  and
and  with
with 

Proof.
If we let  , then it suffices to show that
, then it suffices to show that  . For every
. For every 

By (4.24), (4.35), and (4.36), we see that the first sum  has the form of
has the form of

Then since

we know that  . By (4.37) and (4.7), the second sum
. By (4.37) and (4.7), the second sum  is bounded by
is bounded by  . Here, we can make
. Here, we can make  for arbitrary positive
for arbitrary positive  . Therefore, we obtain the following result: for every
. Therefore, we obtain the following result: for every 

Then the following theorem is important to show a divergence theorem with respect to  where
where  is an odd integer.
is an odd integer.
Theorem 4.10 (cf. [10, ( )] and [15]).
)] and [15]).
For  , there is a polynomial
, there is a polynomial  of degree
of degree  such that
such that  for
for  and the following relation holds. Let
and the following relation holds. Let  . Then one has an expression for
. Then one has an expression for  , and
, and  :
:

where  satisfies that for
satisfies that for  and for
and for 

Proof.
We prove (4.44) by induction on  . Since
. Since  and
and  , (4.44) holds for
, (4.44) holds for  . From (4.28) we write
. From (4.28) we write  in the form of
in the form of

Then by (4.12) and (4.14),  is bounded by
is bounded by  . For
. For  we suppose (4.44) and (4.45). Then we have for
we suppose (4.44) and (4.45). Then we have for 

where  and
and  which are defined in (4.11) and (4.44). Then using Lemma 4.9 and
which are defined in (4.11) and (4.44). Then using Lemma 4.9 and  we have the following form:
we have the following form:

Here, since

we see that  . Therefore, we proved the result.
. Therefore, we proved the result.
References
Levin E, Lubinsky DS: Orthogonal Polynomials for Exponential Weights, CMS Books in Mathematics/Ouvrages de Mathématiques de la SMC, 4. Springer, New York, NY, USA; 2001:xii+476.
Jung HS, Sakai R: Inequalities with exponential weights. Journal of Computational and Applied Mathematics 2008, 212(2):359–373. 10.1016/j.cam.2006.12.011
Jung HS, Sakai R: Orthonormal polynomials with exponential-type weights. Journal of Approximation Theory 2008, 152(2):215–238. 10.1016/j.jat.2007.12.004
Jung HS, Sakai R: Specific examples of exponential weights. Communications of the Korean Mathematical Society 2009, 24(2):303–319. 10.4134/CKMS.2009.24.2.303
Kasuga T, Sakai R: Uniform or mean convergence of Hermite-Fejér interpolation of higher order for Freud weights. Journal of Approximation Theory 1999, 101(2):330–358. 10.1006/jath.1999.3371
Kasuga T, Sakai R: Orthonormal polynomials with generalized Freud-type weights. Journal of Approximation Theory 2003, 121(1):13–53. 10.1016/S0021-9045(02)00041-2
Kasuga T, Sakai R: Orthonormal polynomials for generalized Freud-type weights and higher-order Hermite-Fejér interpolation polynomials. Journal of Approximation Theory 2004, 127(1):1–38. 10.1016/j.jat.2004.01.006
Kasuga T, Sakai R: Orthonormal polynomials for Laguerre-type weights. Far East Journal of Mathematical Sciences 2004, 15(1):95–105.
Kasuga T, Sakai R: Conditions for uniform or mean convergence of higher order Hermite-Fejér interpolation polynomials with generalized Freud-type weights. Far East Journal of Mathematical Sciences 2005, 19(2):145–199.
Kanjin Y, Sakai R: Pointwise convergence of Hermite-Fejér interpolation of higher order for Freud weights. The Tohoku Mathematical Journal 1994, 46(2):181–206. 10.2748/tmj/1178225757
Kanjin Y, Sakai R: Convergence of the derivatives of Hermite-Fejér interpolation polynomials of higher order based at the zeros of Freud polynomials. Journal of Approximation Theory 1995, 80(3):378–389. 10.1006/jath.1995.1024
Sakai R: Hermite-Fejér interpolation. In Approximation Theory (Kecskemét, 1990), Colloquia Mathematica Societatis Janos Bolyaiá. Volume 58. North-Holland, Amsterdam, The Netherlands; 1991:591–601.
Sakai R: Hermite-Fejér interpolation prescribing higher order derivatives. In Progress in Approximation Theory. Edited by: Nevai P, Pinkus A. Academic Press, Boston, Mass, USA; 1991:731–759.
Sakai R: Certain unbounded Hermite-Fejér interpolatory polynomial operators. Acta Mathematica Hungarica 1992, 59(1–2):111–114. 10.1007/BF00052097
Sakai R, Vértesi P: Hermite-Fejér interpolations of higher order. III. Studia Scientiarum Mathematicarum Hungarica 1993, 28(1–2):87–97.
Sakai R, Vértesi P: Hermite-Fejér interpolations of higher order. IV. Studia Scientiarum Mathematicarum Hungarica 1993, 28(3–4):379–386.
Jung HS, Sakai R: Derivatives of integrating functions for orthonormal polynomials with exponential-type weights. Journal of Inequalities and Applications 2009, 2009:-22.
Freud G: Orthogonal Polynomials. Pergamon Press, Oxford, UK; 1971.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Jung, H., Sakai, R. Derivatives of Orthonormal Polynomials and Coefficients of Hermite-Fejér Interpolation Polynomials with Exponential-Type Weights. J Inequal Appl 2010, 816363 (2010). https://doi.org/10.1155/2010/816363
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/816363
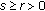
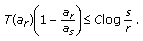
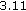 (c)]. (b) It is [
(c)]. (b) It is [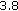 (c)]. (c) It comes from (3.1). (d) Since
(c)]. (c) It comes from (3.1). (d) Since 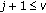 ,
, 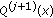 is increasing. So, we obtain (d) by (1.12).
is increasing. So, we obtain (d) by (1.12).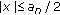 and
and 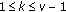 , there exists
, there exists 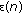 satisfying
satisfying  as
as 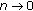 such that
such that , we prove it by Theorem 3.1.
, we prove it by Theorem 3.1.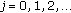 , there exists a unique polynomial
, there exists a unique polynomial 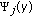 of degree
of degree  such that
such that