- Research Article
- Open access
- Published:
Hyers-Ulam Stability of Differential Equation 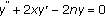
Journal of Inequalities and Applications volume 2010, Article number: 793197 (2009)
Abstract
We solve the inhomogeneous differential equation of the form  , where
, where  is a nonnegative integer, and apply this result to the proof of a local Hyers-Ulam stability of the differential equation
is a nonnegative integer, and apply this result to the proof of a local Hyers-Ulam stability of the differential equation  in a special class of analytic functions.
in a special class of analytic functions.
1. Introduction
Assume that  and
and  are a topological vector space and a normed space, respectively, and that
are a topological vector space and a normed space, respectively, and that  is an open subset of
is an open subset of  . If for any function
. If for any function  satisfying the differential inequality
satisfying the differential inequality

for all  and for some
and for some  , there exists a solution
, there exists a solution  of the differential equation
of the differential equation

such that  for any
for any  , where
, where  is an expression of
is an expression of  only, then we say that the above differential equation satisfies the Hyers-Ulam stability (or the local Hyers-Ulam stability if the domain
only, then we say that the above differential equation satisfies the Hyers-Ulam stability (or the local Hyers-Ulam stability if the domain  is not the whole space
is not the whole space  ). We may apply this terminology for other differential equations. For more detailed definition of the Hyers-Ulam stability, refer to [1–6].
). We may apply this terminology for other differential equations. For more detailed definition of the Hyers-Ulam stability, refer to [1–6].
Obloza seems to be the first author who has investigated the Hyers-Ulam stability of linear differential equations (see [7, 8]). Here, we will introduce a result of Alsina and Ger (see [9]): If a differentiable function  is a solution of the differential inequality
is a solution of the differential inequality  , where
, where  is an open subinterval of
is an open subinterval of  , then there exists a solution
, then there exists a solution  of the differential equation
of the differential equation  such that
such that  for any
for any  .
.
This result of Alsina and Ger has been generalized by Takahasi et al.: They proved in [10] that the Hyers-Ulam stability holds true for the Banach space-valued differential equation  (see also [11]).
(see also [11]).
Using the conventional power series method, the author in [12] investigated the general solution of the inhomogeneous Legendre differential equation of the form

under some specific conditions, where  is a real number and the convergence radius of the power series is positive. Moreover, he applied this result to prove that every analytic function can be approximated in a neighborhood of
is a real number and the convergence radius of the power series is positive. Moreover, he applied this result to prove that every analytic function can be approximated in a neighborhood of  by the Legendre function with an error bound expressed by
by the Legendre function with an error bound expressed by  (see [13–15]).
(see [13–15]).
Let us consider the error function and the complementary error function defined by

respectively. We recursively define the integrals of the error function as follows:

for any  . Suppose that we are given a nonnegative integer
. Suppose that we are given a nonnegative integer  , and we introduce a differential equation
, and we introduce a differential equation

whose general solution is given by

(see [16, §  ]).
]).
In Section 2 of this paper, using power series method, we will investigate the general solution of the inhomogeneous differential equation:

where the radius of convergence of the power series  is
is  , whose value is in general permitted to have infinity. Moreover, using the idea from [12–14], we will prove the Hyers-Ulam stability of the differential equation (1.6) in a class of special analytic functions (see the class
, whose value is in general permitted to have infinity. Moreover, using the idea from [12–14], we will prove the Hyers-Ulam stability of the differential equation (1.6) in a class of special analytic functions (see the class  in Section 3).
in Section 3).
In this paper,  denotes the set of all nonnegative integers.
denotes the set of all nonnegative integers.
2. General Solution of (1.8)
In the following theorem, we solve the inhomogeneous differential equation (1.8).
Theorem 2.1.
Assume that  is a nonnegative integer, the radius of convergence of the power series
is a nonnegative integer, the radius of convergence of the power series  is
is  , and that there exists a real number
, and that there exists a real number  with
with

for all sufficiently large integers  , where
, where

for any  . Let us define
. Let us define  and
and  . Every solution
. Every solution  of the inhomogeneous differential equation (1.8) can be represented by
of the inhomogeneous differential equation (1.8) can be represented by

where  is a solution of the homogeneous differential equation (1.6).
is a solution of the homogeneous differential equation (1.6).
Proof.
Assume that a function  is given by (2.3). We first prove that the function
is given by (2.3). We first prove that the function  , defined by
, defined by  , satisfies the inhomogeneous differential equation (1.8). Since
, satisfies the inhomogeneous differential equation (1.8). Since

we have

for all  .
.
It is not difficult to see that

for any  . Hence, we obtain
. Hence, we obtain

which proves that  is a particular solution of the inhomogeneous equation (1.8).
is a particular solution of the inhomogeneous equation (1.8).
We now apply the ratio test to the power series expression of  . If
. If  is an odd integer not less than
is an odd integer not less than  , then
, then  . Hence, the power series
. Hence, the power series  is a polynomial. And it follows from the first conditions of (2.1) and (2.6) that
is a polynomial. And it follows from the first conditions of (2.1) and (2.6) that

If  is an even integer, then we have
is an even integer, then we have  . Thus, for each even integer
. Thus, for each even integer  , the power series
, the power series  is a polynomial. By the second conditions in (2.1) and (2.6), we get
is a polynomial. By the second conditions in (2.1) and (2.6), we get

Therefore, the power series expression of  converges for all
converges for all  .
.
Moreover, the convergence region of the power series for  is the same as those of power series for
is the same as those of power series for  and
and  . In this paper, the convergence region will denote the maximum open set where the relevant power series converges. Hence, the power series expression for
. In this paper, the convergence region will denote the maximum open set where the relevant power series converges. Hence, the power series expression for  has the same convergence region as that of
has the same convergence region as that of  . This implies that
. This implies that  is well defined on
is well defined on  and so does for
and so does for  in (2.3) because
in (2.3) because  converges for all
converges for all  under our hypotheses.
under our hypotheses.
Since every solution to (1.8) can be expressed as a sum of a solution  of the homogeneous equation and a particular solution
of the homogeneous equation and a particular solution  of the inhomogeneous equation, every solution of (1.8) is certainly in the form of (2.3).
of the inhomogeneous equation, every solution of (1.8) is certainly in the form of (2.3).
Remark 2.2.
We might have thought that the conditions presented in (2.1) were too strong. However, we can show that some familiar sequences  satisfy the conditions in (2.1). For example, let
satisfy the conditions in (2.1). For example, let  and
and  ,
,  for all
for all  and choose an arbitrary
and choose an arbitrary  . Then, by some manipulations, we can show that the coefficients sequence
. Then, by some manipulations, we can show that the coefficients sequence  satisfies the second condition of (2.1) for all sufficiently large integers
satisfies the second condition of (2.1) for all sufficiently large integers  as we see in the following:
as we see in the following:

3. Hyers-Ulam Stability of (1.6)
In this section, let  be a nonnegative integer and let
be a nonnegative integer and let  be a constant with
be a constant with  . For a given
. For a given  , let us denote by
, let us denote by  the set of all functions
the set of all functions  with the properties (a) and (b):
with the properties (a) and (b):
(a) is represented by a power series
is represented by a power series  whose radius of convergence is at least
whose radius of convergence is at least  ;
;
(b)it holds true that  for all
for all  , where
, where  for each
for each  .
.
It should be remarked that the power series  in (b) has the same radius of convergence as that of
in (b) has the same radius of convergence as that of  given in (a).
given in (a).
In the following theorem, we prove that if an analytic function satisfies some given conditions, then it can be approximated by a combination of integrals of the error function (see the last part of Section 1 or [16, §  ]).
]).
Theorem 3.1.
Let  be a nonnegative integer. For given constants
be a nonnegative integer. For given constants  and
and  with
with  and
and  , suppose that
, suppose that  is a function which belongs to
is a function which belongs to  . Assume that there exist constants
. Assume that there exist constants  satisfying
satisfying


for all  .
.  See the definitions of
See the definitions of  and
and  given in Theorem 2.1. Indeed, it is sufficient for the second inequalities in (3.1) and (3.2) to hold true for all sufficiently large integers
given in Theorem 2.1. Indeed, it is sufficient for the second inequalities in (3.1) and (3.2) to hold true for all sufficiently large integers  .
. Let us define
Let us define  , where
, where  . If the function
. If the function  satisfies the differential inequality
satisfies the differential inequality

for all  and for some
and for some  , then there exists a solution
, then there exists a solution  of the differential equation (1.6) such that
of the differential equation (1.6) such that

for any  .
.
Proof.
Since  , it follows from (a) and (b) that
, it follows from (a) and (b) that

for all  . It follows from the last equality and (3.3) that
. It follows from the last equality and (3.3) that

for any  . This inequality, together with (b), yields that
. This inequality, together with (b), yields that

for each  .
.
By Abel's formula (see [17, Theorem  ]), we have
]), we have

for any  and
and  , since
, since

Hence, it follows from (3.7) and (3.8) that

for each  .
.
Finally, it follows from Theorem 2.1, (3.1), (3.2), (3.7), and (3.10) that there exists a solution function  of the homogeneous differential equation (1.6) such that
of the homogeneous differential equation (1.6) such that

for all  .
.
If  is finite, then the local Hyers-Ulam stability of the differential equation (1.6) immediately follows from Theorem 3.1.
is finite, then the local Hyers-Ulam stability of the differential equation (1.6) immediately follows from Theorem 3.1.
Corollary 3.2.
Let  be a nonnegative integer. For given constants
be a nonnegative integer. For given constants  and
and  with
with  and
and  , suppose that
, suppose that  is a function which belongs to
is a function which belongs to  . Assume that there exist constants
. Assume that there exist constants  satisfying the conditions in (3.1) and (3.2) for all
satisfying the conditions in (3.1) and (3.2) for all  .
.  It is sufficient for the second inequalities in (3.1) and (3.2) to hold true for all sufficiently large integers
It is sufficient for the second inequalities in (3.1) and (3.2) to hold true for all sufficiently large integers  .
. Let us define
Let us define  and
and  . If the function
. If the function  satisfies the differential inequality (3.3) for all
satisfies the differential inequality (3.3) for all  and for some
and for some  , then there exists a solution
, then there exists a solution  of the differential equation (1.6) such that
of the differential equation (1.6) such that

for any  .
.
We now deal with an asymptotic behavior of functions in  under the additional conditions (3.1) and (3.2).
under the additional conditions (3.1) and (3.2).
Corollary 3.3.
Let  be a nonnegative integer. For given constants
be a nonnegative integer. For given constants  ,
,  , and
, and  with
with  and
and  , suppose that
, suppose that  is a function belonging to
is a function belonging to  . Assume that there exist constants
. Assume that there exist constants  and
and  satisfying the conditions in (3.1) and (3.2) for any
satisfying the conditions in (3.1) and (3.2) for any  .
.  It is sufficient for the second inequalities in (3.1) and (3.2) to hold true for all sufficiently large integers
It is sufficient for the second inequalities in (3.1) and (3.2) to hold true for all sufficiently large integers  .
. Then there exists a solution
Then there exists a solution  of the differential equation (1.6) such that
of the differential equation (1.6) such that

as  .
.
Proof.
Since  , it follows from the first 4 lines of the proof of Theorem 3.1 that
, it follows from the first 4 lines of the proof of Theorem 3.1 that

for all  . As was remarked in the first part of Section 3, the radius of convergence of the power series
. As was remarked in the first part of Section 3, the radius of convergence of the power series  is same as that of
is same as that of  , that is, it is at least
, that is, it is at least  . Since
. Since  , if we set
, if we set  , then there exists a constant
, then there exists a constant  such that
such that

for any  .
.
According to Theorem 3.1, there exists a solution  of the differential equation (1.6) satisfying
of the differential equation (1.6) satisfying

for any  . Hence, we have
. Hence, we have

as  .
.
4. An Example
The conditions in (3.1) and (3.2) may seem too strong to construct some examples for the coefficients  's. In this section, however, we will show that the sequence
's. In this section, however, we will show that the sequence  given in Remark 2.2 satisfies these conditions: let
given in Remark 2.2 satisfies these conditions: let  and
and  ,
,  for all
for all  and choose some constants
and choose some constants  and
and  . The second inequality in (3.2) has been verified in Remark 2.2.
. The second inequality in (3.2) has been verified in Remark 2.2.
The first inequality in (3.2) is also true for all  as we see in the following:
as we see in the following:

where  denotes the largest integer not exceeding
denotes the largest integer not exceeding  .
.
It is not difficult to show that


for all  .
.
By using (4.2), we will now prove that

as  : if
: if  for some
for some  , then
, then

If  for some
for some  , then
, then

It then follows from (4.3) and (4.4) that

for all sufficiently large integers  , which proves that the sequence
, which proves that the sequence  satisfies the second inequality in (3.1).
satisfies the second inequality in (3.1).
Finally, we will show that the sequence  satisfies the first inequality in (3.1). It follows from (4.3) that
satisfies the first inequality in (3.1). It follows from (4.3) that

for each  .
.
References
Czerwik S: Functional Equations and Inequalities in Several Variables. World Scientific, River Edge, NJ, USA; 2002:x+410.
Hyers DH: On the stability of the linear functional equation. Proceedings of the National Academy of Sciences of the United States of America 1941, 27(4):222–224. 10.1073/pnas.27.4.222
Hyers DH, Isac G, Rassias ThM: Stability of Functional Equations in Several Variables, Progress in Nonlinear Differential Equations and Their Applications, 34. Birkhäuser, Boston, Mass, USA; 1998:vi+313.
Jung S-M: Hyers-Ulam-Rassias Stability of Functional Equations in Mathematical Analysis. Hadronic Press, Palm Harbor, Fla, USA; 2001:ix+256.
Rassias ThM: On the stability of the linear mapping in Banach spaces. Proceedings of the American Mathematical Society 1978, 72(2):297–300. 10.1090/S0002-9939-1978-0507327-1
Ulam SM: A Collection of Mathematical Problems, Interscience Tracts in Pure and Applied Mathematics, no. 8. Interscience, London, UK; 1960:xiii+150.
Obłoza M: Hyers stability of the linear differential equation. Rocznik Naukowo-Dydaktyczny. Prace Matematyczne 1993, (13):259–270.
Obłoza M: Connections between Hyers and Lyapunov stability of the ordinary differential equations. Rocznik Naukowo-Dydaktyczny. Prace Matematyczne 1997, (14):141–146.
Alsina C, Ger R: On some inequalities and stability results related to the exponential function. Journal of Inequalities and Applications 1998, 2(4):373–380. 10.1155/S102558349800023X
Takahasi S-E, Miura T, Miyajima S: On the Hyers-Ulam stability of the Banach space-valued differential equation . Bulletin of the Korean Mathematical Society 2002, 39(2):309–315. 10.4134/BKMS.2002.39.2.309
Miura T, Jung S-M, Takahasi S-E: Hyers-Ulam-Rassias stability of the Banach space valued linear differential equations . Journal of the Korean Mathematical Society 2004, 41(6):995–1005. 10.4134/JKMS.2004.41.6.995
Jung S-M: Legendre's differential equation and its Hyers-Ulam stability. Abstract and Applied Analysis 2007, 2007:-14.
Jung S-M: Approximation of analytic functions by Airy functions. Integral Transforms and Special Functions 2008, 19(11–12):885–891.
Jung S-M: Approximation of analytic functions by Hermite functions. Bulletin des Sciences Mathematiques 2009, 133(7):756–764. 10.1016/j.bulsci.2007.11.001
Kim B, Jung S-M: Bessel's differential equation and its Hyers-Ulam stability. Journal of Inequalities and Applications 2007, 2007:-8.
Abramowitz M, Stegun IA: Handbook of Mathematical Functions. Dover, New York, NY, USA; 1972.
Wade WR: An Introduction to Analysis. 2nd edition. Prentice Hall, Upper Saddle River, NJ, USA; 2000.
Acknowledgments
The author would like to express his cordial thanks to the referee for useful remarks which have improved the first version of this paper. This work was supported by the National Research Foundation of Korea Grant funded by the Korean Government (no. 2009-0071206).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Jung, SM. Hyers-Ulam Stability of Differential Equation 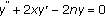 .
J Inequal Appl 2010, 793197 (2009). https://doi.org/10.1155/2010/793197
.
J Inequal Appl 2010, 793197 (2009). https://doi.org/10.1155/2010/793197
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/793197