- Research Article
- Open access
- Published:
The Obstacle Problem for the 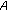 -Harmonic Equation
-Harmonic Equation
Journal of Inequalities and Applications volume 2010, Article number: 767150 (2010)
Abstract
Firstly, we define an order for differential forms. Secondly, we also define the supersolution and subsolution of the  -harmonic equation and the obstacle problems for differential forms which satisfy the
-harmonic equation and the obstacle problems for differential forms which satisfy the  -harmonic equation, and we obtain the relations between the solutions to
-harmonic equation, and we obtain the relations between the solutions to  -harmonic equation and the solution to the obstacle problem of the
-harmonic equation and the solution to the obstacle problem of the  -harmonic equation. Finally, as an application of the obstacle problem, we prove the existence and uniqueness of the solution to the
-harmonic equation. Finally, as an application of the obstacle problem, we prove the existence and uniqueness of the solution to the  -harmonic equation on a bounded domain
-harmonic equation on a bounded domain  with a smooth boundary
with a smooth boundary  , where the
, where the  -harmonic equation satisfies
-harmonic equation satisfies  where
where  is any given differential form which belongs to
is any given differential form which belongs to  .
.
1. Introduction
Recently, a large amount of work about the  -harmonic equation for the differential forms has been done. In 1999 Nolder gave some properties for the solution to the
-harmonic equation for the differential forms has been done. In 1999 Nolder gave some properties for the solution to the  -harmonic equation in [1], and different versions of these properties had been established in [2–4]. The properties of the nonhomogeneous
-harmonic equation in [1], and different versions of these properties had been established in [2–4]. The properties of the nonhomogeneous  -harmonic equation have been discussed in [5–10]. In the above papers, we can think that the boundary values were zero. In this paper, we mainly discuss the existence and uniqueness of the solution to
-harmonic equation have been discussed in [5–10]. In the above papers, we can think that the boundary values were zero. In this paper, we mainly discuss the existence and uniqueness of the solution to  -harmonic equation with boundary values on a bounded domain
-harmonic equation with boundary values on a bounded domain  .
.
Now let us see some notions and definitions about the  -harmonic equation
-harmonic equation  .
.
Let  denote the standard orthogonal basis of
denote the standard orthogonal basis of  . For
. For  we denote by
we denote by  the linear space of all
the linear space of all  -vectors, spanned by the exterior product
-vectors, spanned by the exterior product  corresponding to all ordered
corresponding to all ordered  -tuples
-tuples  ,
,  . The Grassmann algebra
. The Grassmann algebra  is a graded algebra with respect to the exterior products of
is a graded algebra with respect to the exterior products of  and
and  , then its inner product is obtained by
, then its inner product is obtained by

with the summation over all  and all integers
and all integers  . And the norm of
. And the norm of  is given by
is given by  .
.
The Hodge star operator  :
: is defined by the rule if
is defined by the rule if  , then
, then

where  and
and  So we have
So we have 
Throughout this paper,  is an open subset, for any constant
is an open subset, for any constant  ,
,  denotes a cube such that
denotes a cube such that  , where
, where  denotes the cube whose center is as same as
denotes the cube whose center is as same as  and
and  . We say that
. We say that  is a differential
is a differential  -form on
-form on  if every coefficient
if every coefficient  of
of  is Schwartz distribution on
is Schwartz distribution on  . The space spanned by differential
. The space spanned by differential  -form on
-form on  is denoted by
is denoted by  . We write
. We write  for the
for the  -form
-form  on
on  with
with  for all ordered
for all ordered  -tuple
-tuple  . Thus
. Thus  is a Banach space with the norm
is a Banach space with the norm

Similarly  denotes those
denotes those  -forms on
-forms on  with all coefficients in
with all coefficients in  . We denote the exterior derivative by
. We denote the exterior derivative by

and its formal adjoint operator (the Hodge codifferential operator)

The operators  and
and  are given by the formulas
are given by the formulas

2. The Obstacle Problem
In this section, we introduce the main work of this paper, which defining the supersolution and subsolution of the  -harmonic equation and the obstacle problems for differential forms which satisfy the
-harmonic equation and the obstacle problems for differential forms which satisfy the  -harmonic equation, and the proof for the uniqueness of the solution to the obstacle problem of the
-harmonic equation, and the proof for the uniqueness of the solution to the obstacle problem of the  -harmonic equations for differential forms. We can see this work about functions in [11, Chapter 3 and Appendix
-harmonic equations for differential forms. We can see this work about functions in [11, Chapter 3 and Appendix  ] in detail. We use the similar methods in [11] to do the main work for differential forms.
] in detail. We use the similar methods in [11] to do the main work for differential forms.
We firstly give the comparison about differential forms according to the comparison's definition about functions in  .
.
Definition 2.1.
Suppose that  and
and  belong to
belong to  , we say that
, we say that  if for any given
if for any given  , we have
, we have  for all ordered
for all ordered  -tuples
-tuples  ,
,  .
.
Remark 2.2.
The above definition involves the order for differential forms which we have been trying to avoid giving. We know that many differential forms can not be compared based on the above definition since there are so many inequalities to be satisfied. However, at the moment, we can not replace this definition by another one and we are working on it now. We just started our research on the obstacle problem for differential forms satisfying the  -harmonic equation and we hope that our work will stimulate further research in this direction.
-harmonic equation and we hope that our work will stimulate further research in this direction.
By the some definitions as the solution, supersolution (or subsolution) to quasilinear elliptic equation, we can give the definitions of the solution, supersolution (or subsolution) to  -harmonic equation
-harmonic equation

Definition 2.3.
If a differential form  satisfies
satisfies

for any  , then we say that
, then we say that  is a solution to (2.1). If for any
is a solution to (2.1). If for any  , we have
, we have

then we say that  is a supersolution (subsolution) to (2.1).
is a supersolution (subsolution) to (2.1).
We can see that if  is a subsolution to (2.1), then for
is a subsolution to (2.1), then for  , we have
, we have

According to the above definition, we can get the following theorem.
Theorem 2.4.
A differential form  is a solution to (2.1) if and only if
is a solution to (2.1) if and only if  is both supersolution and subsolution to (2.1).
is both supersolution and subsolution to (2.1).
Proof.
The sufficiency is obvious, we only prove the necessity. For any  , we suppose that
, we suppose that  ,
,

by Definition 2.3, it holds that

So

Using  in place of
in place of  , we also can get
, we also can get

Thus

Therefore  is a solution to (2.1).
is a solution to (2.1).
Next we will introduce the obstacle problem to  -harmonic equation, whose definition is according to the same definition as the obstacle problem of quasilinear elliptic equation. For the obstacle problem of quasilinear elliptic equation we can see [11] for details.
-harmonic equation, whose definition is according to the same definition as the obstacle problem of quasilinear elliptic equation. For the obstacle problem of quasilinear elliptic equation we can see [11] for details.
Suppose that  is a bounded domain. that
is a bounded domain. that  is any differential form in
is any differential form in  which satisfies any
which satisfies any  that is function in
that is function in  with values in the extended reals
with values in the extended reals  , and
, and  . Let
. Let

The problem is to find a differential form in  such that for any
such that for any  , we have
, we have

Definition 2.5.
A differential form  is called a solution to the obstacle problem of
is called a solution to the obstacle problem of  -harmonic equation (2.1) with obstacle
-harmonic equation (2.1) with obstacle  and boundary values
and boundary values  or a solution to the obstacle problem of
or a solution to the obstacle problem of  -harmonic equation (2.1) in
-harmonic equation (2.1) in  if
if  satisfies (2.11) for any
satisfies (2.11) for any  .
.
If  , then we denote that
, then we denote that  We have some relations between the solution to quasilinear elliptic equation and the solution to obstacle problem in PDE. As to differential forms, we also have some relations between the solution to
We have some relations between the solution to quasilinear elliptic equation and the solution to obstacle problem in PDE. As to differential forms, we also have some relations between the solution to  -harmonic equation and the solution to obstacle problem of
-harmonic equation and the solution to obstacle problem of  -harmonic equation. We have the following two theorems.
-harmonic equation. We have the following two theorems.
Theorem 2.6.
If a differential form  is a supersolution to (2.1), then
is a supersolution to (2.1), then  is a solution to the obstacle problem of (2.1) in
is a solution to the obstacle problem of (2.1) in  . For any
. For any  , if
, if  is a solution to the obstacle problem of (2.1) in
is a solution to the obstacle problem of (2.1) in  , then
, then  is a supersolution to (2.1) in
is a supersolution to (2.1) in  .
.
Proof.
If  is a solution to the obstacle problem of (2.1) in
is a solution to the obstacle problem of (2.1) in  , then for any
, then for any  , we have
, we have  , so it holds that
, so it holds that

Thus  is a supersolution to (2.1) in
is a supersolution to (2.1) in  . Conversely, if
. Conversely, if  is a supersolution to (2.1) in
is a supersolution to (2.1) in  , then for any
, then for any  , we have
, we have

Thus let  , then we have
, then we have

So  is a solution to the obstacle problem of (2.1) in
is a solution to the obstacle problem of (2.1) in  .
.
Theorem 2.7.
A differential form  is a solution to (2.1) if and only if
is a solution to (2.1) if and only if  is a solution to the obstacle problem of (2.1) in
is a solution to the obstacle problem of (2.1) in  with
with  satisfying
satisfying  .
.
Proof.
If is a solution to the obstacle problem of (2.1) in  , then for any
, then for any  , we have
, we have  . So we can obtain
. So we can obtain

By using  in place of
in place of  , we have
, we have

So

Thus  is a solution to (2.1) in
is a solution to (2.1) in  .
.
Conversely, if  is a solution to (2.1) in
is a solution to (2.1) in  , then for any
, then for any  , we have
, we have  Now let
Now let  , then we have
, then we have

Thus

So the theorem is proved.
The following we will discuss the existence and uniqueness of the solution to the obstacle problem of (2.1) in  and the solution to (2.1). First we introduce a definition and two lemmas.
and the solution to (2.1). First we introduce a definition and two lemmas.
Definition 2.8 (see [11]).
Suppose that  is a reflexive Banach space in
is a reflexive Banach space in  with dual space
with dual space  , and let
, and let  denote a pairing between
denote a pairing between  and
and  . If
. If  is a closed convex set, then a mapping
is a closed convex set, then a mapping  is called monotone if
is called monotone if

for all  in
in  . Further,
. Further,  is called coercive on
is called coercive on  if there exists
if there exists  such that
such that

whenever  is a sequence in
is a sequence in  with
with  .
.
By the definition of  in [12], we can easily get the following lemma.
in [12], we can easily get the following lemma.
Lemma 2.9.
For any  , we have
, we have  and
and  .
.
Lemma 2.10 (see [11]).
Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  and let
and let  be monotone, coercive, and weakly continuous on
be monotone, coercive, and weakly continuous on  . Then there exists an element
. Then there exists an element  in
in  such that
such that

whenever  .
.
Using the same methods in [11, Appendix  ], we can prove the existence and uniqueness of the solution to the obstacle problem of (2.1).
], we can prove the existence and uniqueness of the solution to the obstacle problem of (2.1).
Theorem 2.11.
If  is nonempty, then there exists a unique solution to the obstacle problem of (2.1) in
is nonempty, then there exists a unique solution to the obstacle problem of (2.1) in  .
.
Proof.
Let  , then
, then  . Let
. Let

where  and
and  . Denote that
. Denote that

We define a mapping  such that for any
such that for any  , we have
, we have  . So for any
. So for any  , we have
, we have

Then we only prove that  is a closed convex subset of
is a closed convex subset of  and
and  is monotone, coercive, and weakly continuous on
is monotone, coercive, and weakly continuous on  .
.
( )
)  is convex. For any
is convex. For any  , we have
, we have  such that
such that

So for any  , we have
, we have

Since

thus

So  is convex.
is convex.
( )
)  is closed in
is closed in  . Suppose that
. Suppose that  is a sequence converging to
is a sequence converging to  in
in  . Then by the real functions' Poincaré inequality and Lemma 2.9, we have
. Then by the real functions' Poincaré inequality and Lemma 2.9, we have

Thus  is a bounded sequence in
is a bounded sequence in  . Because
. Because  is a closed and convex subset of
is a closed and convex subset of  , we denote that
, we denote that  and
and  . Then for any
. Then for any  in
in  tuples, according to Theorems
tuples, according to Theorems  and
and  in [11], we have a function
in [11], we have a function  such that
such that

According to Lemma 2.9 and the uniqueness of a limit of a convergence sequence, we only let

Thus  , so
, so  is closed in
is closed in  .
.
( )
) is monotone. Since operator
is monotone. Since operator  satisfies
satisfies

so for all  , it holds that
, it holds that

Thus  is monotone.
is monotone.
( )
)  is coercive on
is coercive on  . For any fixed
. For any fixed  , we have
, we have

So

When  and
and  , we can obtain
, we can obtain

Therefore  is coercive on
is coercive on  .
.
(5) is weakly continuous on
is weakly continuous on  . Suppose that
. Suppose that  is a sequence that converge to
is a sequence that converge to  on
on  . Pick a subsequence
. Pick a subsequence  such that
such that  a.e. in
a.e. in  . Since the mapping
. Since the mapping  is continuous for a.e.
is continuous for a.e.  , we have
, we have

a.e.  . Because
. Because  -norms of
-norms of  are uniformly bounded, we have that
are uniformly bounded, we have that

weakly in  . Because the weak limit is independent of the choice of the subsequence, it follows that
. Because the weak limit is independent of the choice of the subsequence, it follows that

weakly in  . Thus for any
. Thus for any  , we have
, we have

Thus  is weakly continuous on
is weakly continuous on  .
.
By Lemma 2.10, we can find an element  in
in  such that
such that

for any  , that is to say, there exists
, that is to say, there exists  such that
such that  and
and

for any  . Then the theorem is proved.
. Then the theorem is proved.
By Theorem 2.7, we can see that the solution  to the obstacle problem of (2.1) in
to the obstacle problem of (2.1) in  is a solution of (2.1) in
is a solution of (2.1) in  . Then by theorem, we can get the existence and uniqueness of the solution to
. Then by theorem, we can get the existence and uniqueness of the solution to  -harmonic equation.
-harmonic equation.
Corollary 2.12.
Suppose that  is a bounded domain with a smooth boundary
is a bounded domain with a smooth boundary  and
and  . There is a differential form
. There is a differential form  such that
such that

weakly in  , that is to say,
, that is to say,

for any  .
.
Proof.
Let  and
and  be a solution to the obstacle problem of (2.1) in
be a solution to the obstacle problem of (2.1) in  . For any
. For any  , we have both
, we have both  and
and  belong to
belong to  . Then
. Then

Thus

So  is solution to
is solution to  -harmonic equation
-harmonic equation  in
in  with a boundary value
with a boundary value  .
.
References
Nolder CA: Hardy-Littlewood theorems for -harmonic tensors. Illinois Journal of Mathematics 1999, 43(4):613–632.
Ding S: Weighted Caccioppoli-type estimates and weak reverse Hölder inequalities for -harmonic tensors. Proceedings of the American Mathematical Society 1999, 127(9):2657–2664. 10.1090/S0002-9939-99-05285-5
Bao G: -weighted integral inequalities for -harmonic tensors. Journal of Mathematical Analysis and Applications 2000, 247(2):466–477. 10.1006/jmaa.2000.6851
Yuming X: Weighted integral inequalities for solutions of the -harmonic equation. Journal of Mathematical Analysis and Applications 2003, 279(1):350–363. 10.1016/S0022-247X(03)00036-2
Ding S: Two-weight Caccioppoli inequalities for solutions of nonhomogeneous -harmonic equations on Riemannian manifolds. Proceedings of the American Mathematical Society 2004, 132(8):2367–2395. 10.1090/S0002-9939-04-07347-2
D'Onofrio L, Iwaniec T: The -harmonic transform beyond its natural domain of definition. Indiana University Mathematics Journal 2004, 53(3):683–718. 10.1512/iumj.2004.53.2462
Ding S: Local and global norm comparison theorems for solutions to the nonhomogeneous -harmonic equation. Journal of Mathematical Analysis and Applications 2007, 335(2):1274–1293. 10.1016/j.jmaa.2007.02.048
Cao Z, Bao G, Li R, Zhu H: The reverse Hölder inequality for the solution to -harmonic type system. Journal of Inequalities and Applications 2008, 2008:-15.
Bao G, Cao Z, Li R: The Caccioppoli estimates for the solutions to -harmonic type equation. Dynamics of Continuous, Discrete & Impulsive Systems. Series A 2009, 16(S1):104–108.
Cao Z, Bao G, Xing Y, Li R: Some Caccioppoli estimates for differential forms. Journal of Inequalities and Applications 2009, 2009:-11.
Heinonen J, Kilpeläìnen T, Martio O: Nonlinear Potential Theory of Degenerate Elliptic Equations, Oxford Mathematical Monographs. Oxford University Press, New York, NY, USA; 1993:vi+363.
Iwaniec T, Lutoborski A: Integral estimates for null Lagrangians. Archive for Rational Mechanics and Analysis 1993, 125(1):25–79. 10.1007/BF00411477
Acknowledgment
This work is supported by the NSF of P.R. China (no. 10771044).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Cao, Z., Bao, G. & Zhu, H. The Obstacle Problem for the 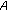 -Harmonic Equation.
J Inequal Appl 2010, 767150 (2010). https://doi.org/10.1155/2010/767150
-Harmonic Equation.
J Inequal Appl 2010, 767150 (2010). https://doi.org/10.1155/2010/767150
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/767150