- Research Article
- Open access
- Published:
Relative Isoperimetric Inequality for Minimal Submanifolds in a Riemannian Manifold
Journal of Inequalities and Applications volume 2010, Article number: 758623 (2010)
Abstract
Let  be a domain on an
be a domain on an  -dimensional minimal submanifold in the outside of a convex set
-dimensional minimal submanifold in the outside of a convex set  in
in  or
or  . The modified volume
. The modified volume  is introduced by Choe and Gulliver (1992) and we prove a sharp modified relative isoperimetric inequality for the domain
is introduced by Choe and Gulliver (1992) and we prove a sharp modified relative isoperimetric inequality for the domain  ,
,  , where
, where  is the volume of the unit ball of
is the volume of the unit ball of  . For any domain
. For any domain  on a minimal surface in the outside convex set
on a minimal surface in the outside convex set  in an
in an  -dimensional Riemannian manifold, we prove a weak relative isoperimetric inequality
-dimensional Riemannian manifold, we prove a weak relative isoperimetric inequality  , where
, where  is an upper bound of sectional curvature of the Riemannian manifold.
is an upper bound of sectional curvature of the Riemannian manifold.
1. Introduction
Let  be the simple closed curve of a domain
be the simple closed curve of a domain  in a two-dimensional space form with constant curvature
in a two-dimensional space form with constant curvature  . Then the well-known sharp isoperimetric inequality is the following:
. Then the well-known sharp isoperimetric inequality is the following:

where equality holds if and only if  is a geodesic disk (see [1]).
is a geodesic disk (see [1]).
An immediate consequence of this inequality is that if  is a closed half-space of a two-dimensional space form with constant curvature
is a closed half-space of a two-dimensional space form with constant curvature  and
and  is a domain in
is a domain in  with
with  , then
, then

where equality holds if and only if  is a totally geodesic half-disk with the geodesic part of its boundary contained in
is a totally geodesic half-disk with the geodesic part of its boundary contained in  . This follows the original isoperimetric inequality after extending the domain by mirror symmetry with respect to
. This follows the original isoperimetric inequality after extending the domain by mirror symmetry with respect to  .
.
Motivated by this, one arises natural questions as follows.
If  is a convex set in an
is a convex set in an  -dimensional space form with constant curvature
-dimensional space form with constant curvature  and
and  is a minimal surface in the outside of
is a minimal surface in the outside of  with
with  , does
, does  satisfy inequality
satisfy inequality

How about an  -dimensional minimal submanifold case?
-dimensional minimal submanifold case?
Equation (1.3) is called the relative isoperimetric inequality,  is called the supporting set of
is called the supporting set of  , and
, and  is called the relative area of
is called the relative area of  . A partial result is obtained by Kim [2], when part of the boundary
. A partial result is obtained by Kim [2], when part of the boundary  of the domain
of the domain  is radially connected from a point
is radially connected from a point  , that is,
, that is,  is a connected interval. And there are some partial results on the higher-dimensional submanifold case (see [3, 4]). In case of
is a connected interval. And there are some partial results on the higher-dimensional submanifold case (see [3, 4]). In case of  , the problem remains open, even in the two-dimensional case (see [5]).
, the problem remains open, even in the two-dimensional case (see [5]).
In this paper, we obtain two different type relative isoperimetric inequalities. First, using the modified volume introduced by Choe and Gulliver [6], we have a modified relative isoperimetric inequality in  or
or  without the curvature correct term:
without the curvature correct term:

where  is the volume of a unit ball of
is the volume of a unit ball of  , and
, and  is a domain of an
is a domain of an  -dimensional submanifold. In Theorem 2.11, (1.4) holds for
-dimensional submanifold. In Theorem 2.11, (1.4) holds for  lies on a geodesic sphere of
lies on a geodesic sphere of  or
or  . In Theorem 2.3, (1.4) holds for
. In Theorem 2.3, (1.4) holds for  ,
,  and
and  is radially connected for a point
is radially connected for a point  .
.
Second, in Section 3 we obtain an inequality on usual volume for any minimal surface of a Riemannian manifold with sectional curvature bounded above by a constant  :
:

But we cannot find a minimal surface which satisfies the equality. That is why we call (1.5) a weak relative isoperimetric inequality.
2. Modified Relative Isoperimetric Inequalities in a Space Form
We review the modified volume in  and
and  with constant sectional curvature
with constant sectional curvature  and
and  , respectively. Let
, respectively. Let  be a point in the
be a point in the  -dimensional sphere
-dimensional sphere  and let
and let  be the distance from
be the distance from  to
to  in
in  .
.
Definition 2.1 (modified volume in  ).
).
Given that  is an
is an  -dimensional submanifold in
-dimensional submanifold in  , the modified volume of
, the modified volume of  with center at
with center at  is defined by
is defined by

Embed  in
in  with
with  being the north pole
being the north pole  . For a domain, the geometric meaning of the modified volume of
. For a domain, the geometric meaning of the modified volume of  is the Euclidean volume of the orthogonal projection of
is the Euclidean volume of the orthogonal projection of  into the
into the  counting orientation. Clearly, we have in
counting orientation. Clearly, we have in 

where  is the usual volume of
is the usual volume of  .
.
Similarly, let  be a point in the
be a point in the  -dimensional hyperbolic space
-dimensional hyperbolic space  and let
and let  be the distance from
be the distance from  to
to  in
in  .
.
Definition 2.2 (modified volume in  ).
).
Given that  is an
is an  -dimensional submanifold in
-dimensional submanifold in  , the modified volume of
, the modified volume of  with center at
with center at  is defined by
is defined by

Embed  isometrically onto the hyperboloid
isometrically onto the hyperboloid  in
in  with the Minkowski metric
with the Minkowski metric  such that
such that  is the point
is the point  . Then for a domain, the modified volume equals the Euclidean volume of the projection of
. Then for a domain, the modified volume equals the Euclidean volume of the projection of  onto the hyperplane
onto the hyperplane  . Clearly, we have in
. Clearly, we have in 

More precisely, see Choe and Gulliver's paper (see [6]).
Theorem 2.3.
Let  be a closed convex set in
be a closed convex set in  . Assume that
. Assume that  is a compact minimal surface in the outside
is a compact minimal surface in the outside  such that
such that  is orthogonal to
is orthogonal to  along
along  . And
. And  is the distance from
is the distance from  to
to  and
and  on
on  . If
. If  is radially connected from the point
is radially connected from the point  , that is,
, that is,  is a connected interval, then one has
is a connected interval, then one has

Equality holds if and only if  is a totally geodesic half-disk with
is a totally geodesic half-disk with  being a geodesic half-circle.
being a geodesic half-circle.
If  is connected, then it is trivially radially connected from
is connected, then it is trivially radially connected from  . If
. If  has two components, then using the same argument as [2, Corollary
has two components, then using the same argument as [2, Corollary  ] we obtain the following.
] we obtain the following.
Corollary 2.4.
Let  be a compact minimal surface satisfying the same assumptions as in Theorem 2.3 except the radially connectedness. Then the modified relative isoperimetric inequality in Theorem 2.3 holds if
be a compact minimal surface satisfying the same assumptions as in Theorem 2.3 except the radially connectedness. Then the modified relative isoperimetric inequality in Theorem 2.3 holds if  is connected or
is connected or  has two components that are connected by a component
has two components that are connected by a component  of
of 
Before giving lemmas for proving Theorem 2.3, we define a cone. Given an  -dimensional submanifold
-dimensional submanifold  of
of  or
or  and a point
and a point  in
in  or
or  , the
, the  -dimensional cone
-dimensional cone  with center at
with center at  is defined by the set of all minimizing geodesics from
is defined by the set of all minimizing geodesics from  to a point of
to a point of  .
.
Lemma 2.5 (see [6, Lemma 4]).
-
(a)
If
 is an
is an 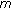 -dimensional minimal submanifold or a cone, and
-dimensional minimal submanifold or a cone, and  is the distance in
is the distance in 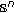 from a fixed point, then
from a fixed point, then 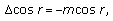 (2.6)
(2.6)
where  is the Laplacian on the submanifold
is the Laplacian on the submanifold  and, in case
and, in case  is a cone,
is a cone,  is the distance from the center of
is the distance from the center of  .
.
-
(b)
Suppose that
 is an
is an  -dimensional minimal submanifold or a cone. Then
-dimensional minimal submanifold or a cone. Then

Here again, in case of a cone  ,
,  is the distance from the center of
is the distance from the center of  .
.
Proposition 2.6.
Let  be a closed convex set in
be a closed convex set in  or
or  . Assume that
. Assume that  is an m-dimensional minimal submanifold in the outside
is an m-dimensional minimal submanifold in the outside  such that
such that  is orthogonal to
is orthogonal to  along
along  and
and  is the distance from
is the distance from  to
to  or
or  . Let
. Let  . In case of
. In case of  , one assumes that
, one assumes that  for all
for all  . Then one has
. Then one has

Proof.
Let  and
and  be the unit conomals to
be the unit conomals to  on
on  and
and  , respectively. By Lemma 2.5, we have
, respectively. By Lemma 2.5, we have

The  makes the smallest angle with
makes the smallest angle with  , that is, the unit normal vector to
, that is, the unit normal vector to  that lies in the two-dimensional plane spanned by
that lies in the two-dimensional plane spanned by  and the tangent line of
and the tangent line of  such that
such that  Clearly
Clearly  where
where  is a unit tangent to
is a unit tangent to  . Since
. Since  is a convex set,
is a convex set,  , and
, and  , we see that
, we see that  points outward of
points outward of  for every
for every  , where
, where  is the gradient in the
is the gradient in the  . From the orthogonality condition,
. From the orthogonality condition,  is a unit normal toward inside
is a unit normal toward inside  along the
along the  . So we have
. So we have

for every  , and
, and

The similar proof holds for 
Lemma 2.7 (see [6, Lemma 6]).
Let  be Green's function of
be Green's function of  (
( , resp.), whose derivative is
, resp.), whose derivative is  for
for  (
( for
for  , resp.). If
, resp.). If  is an
is an  -dimensional minimal submanifold of
-dimensional minimal submanifold of  (
( , resp.), then
, resp.), then  is subharmonic on
is subharmonic on  (
( , resp.).
, resp.).
Now we estimate the angle of  viewed from a point
viewed from a point  Recall the definition of the angle viewed from a point. For an
Recall the definition of the angle viewed from a point. For an  -dimensional rectifiable set
-dimensional rectifiable set  in
in  and a point
and a point  such that
such that  for all
for all  , the
, the  -dimensional angle
-dimensional angle  of
of  viewed from
viewed from  is defined by
is defined by

where  is the geodesic sphere of radius
is the geodesic sphere of radius  centered at
centered at  , and the volume is measured counting multiplicity. Clearly, the angle does not depend on
, and the volume is measured counting multiplicity. Clearly, the angle does not depend on  . There is obviously an analogous definition for the angle of
. There is obviously an analogous definition for the angle of  viewed from
viewed from  .
.
Note that

where  is the
is the  -dimensional density of
-dimensional density of  at
at  .
.
Proposition 2.8.
Let  be an m-dimensional minimal submanifold satisfying the same assumptions as in Proposition 2.6. Then for any
be an m-dimensional minimal submanifold satisfying the same assumptions as in Proposition 2.6. Then for any  ,
,

Equality holds if and only if  is totally geodesic and star shaped with respect to
is totally geodesic and star shaped with respect to  .
.
Proof.
Let  be the geodesic ball centered at
be the geodesic ball centered at  , radius
, radius  ,
,  , and
, and  . By Lemma 2.7, we have subharmonic
. By Lemma 2.7, we have subharmonic  , where
, where  is distance from
is distance from  . Hence
. Hence

where  is outward unit conormal along the boundary.
is outward unit conormal along the boundary.
Since, near  ,
,  can be identified with totally geodesic half-sphere and
can be identified with totally geodesic half-sphere and  and
and  on
on  as
as  , we have
, we have

where  is the unit conormal of the cone and the same argument holds as in Proposition 2.6.
is the unit conormal of the cone and the same argument holds as in Proposition 2.6.
Equality holds if and only if  ,
,  , and
, and  , that is,
, that is,  is a star-shaped minimal cone with density at the center equal to
is a star-shaped minimal cone with density at the center equal to  . Since
. Since  is the only
is the only  -dimensional minimal submanifold in
-dimensional minimal submanifold in  with volume
with volume  , this completes the proof for
, this completes the proof for  . A similar proof holds for
. A similar proof holds for 
Proof of Theorem 2.3.
We approach to the proof by comparison between  and the cone
and the cone  . Since the cone
. Since the cone  is locally developable on a totally geodesic sphere
is locally developable on a totally geodesic sphere  , we reduce the proof to the proof of Theorem
, we reduce the proof to the proof of Theorem  in [7] by doubling argument.
in [7] by doubling argument.
For each geodesic sphere  centered at
centered at  and radius
and radius  , one has a local isometry between the curve
, one has a local isometry between the curve  and a great circle on
and a great circle on  . Hence we can develop
. Hence we can develop  on a great sphere
on a great sphere  ; one can find a curve
; one can find a curve  (not necessarily closed) in
(not necessarily closed) in  and a local isometry from
and a local isometry from  into
into  , where
, where  is the north pole of
is the north pole of  . Clearly we have
. Clearly we have  ,
,  , and
, and  Moreover, if we let
Moreover, if we let  and
and  be the endpoints of
be the endpoints of  , then
, then  .
.
We write  , where
, where  ,
,  , is a connected component of
, is a connected component of  . Note that
. Note that  may be empty or not.
may be empty or not.
If  , then, after cutting
, then, after cutting  along an appropriate geodesic and developing it onto the great sphere
along an appropriate geodesic and developing it onto the great sphere  ,
,  may be identified with the cone
may be identified with the cone  in
in  , where
, where  is a curve in
is a curve in  given in terms of the polar coordinates by
given in terms of the polar coordinates by  satisfying
satisfying  and
and  Here,
Here,  is the angle parameter of the cone. Now we define the doubling
is the angle parameter of the cone. Now we define the doubling  of
of  by the doubling parametrization as follows:
by the doubling parametrization as follows:

If  , then, after developing it onto
, then, after developing it onto  ,
,  is identified with
is identified with  in
in  , where
, where  is a curve in
is a curve in  given in terms of the polar coordinates by
given in terms of the polar coordinates by  defined on
defined on  , where
, where  is the angle parameter of the cone. Choose
is the angle parameter of the cone. Choose  such that
such that  Then we define the doubling
Then we define the doubling  of
of  as follows:
as follows:

In both cases, we have the following equalities:

Now let us define  . Because of doubling process, we have
. Because of doubling process, we have

By Proposition 2.8,  and then
and then  has a self-intersection point. By the geometric meaning of the modified volume,
has a self-intersection point. By the geometric meaning of the modified volume,  equals the Euclidean area of the standard projection of
equals the Euclidean area of the standard projection of  onto the plane containing the equator of
onto the plane containing the equator of  . Let
. Let  be the image of
be the image of  under the projection and
under the projection and  the origin of the plane. Then
the origin of the plane. Then  ,
,  , but
, but  The last inequality arises from the fact that the projection is a length-shrinking map. Moreover, let
The last inequality arises from the fact that the projection is a length-shrinking map. Moreover, let  and
and  be the endpoints of
be the endpoints of  , then
, then  . So we can apply [7, Lemma
. So we can apply [7, Lemma  ] and conclude the following sharp isoperimetric inequality:
] and conclude the following sharp isoperimetric inequality:

and equality holds if and only if  is the boundary of a circle. So we have
is the boundary of a circle. So we have

By Proposition 2.6, we finally get

and equality holds if and only if  and
and  , or equivalently,
, or equivalently,  is a totally geodesic half-disk centered at
is a totally geodesic half-disk centered at  .
.
Proposition 2.9.
Let  be a closed convex set in
be a closed convex set in  (
( , resp.) and let
, resp.) and let  be an
be an  -dimensional compact minimal submanifold of
-dimensional compact minimal submanifold of  (
( , resp.) satisfying that
, resp.) satisfying that  is orthogonal to
is orthogonal to  along
along  . Define
. Define  for
for  . Then
. Then  (
( , resp.) is a monotonically nondecreasing function of
, resp.) is a monotonically nondecreasing function of  for
for  (
( , resp.), where
, resp.), where  is the
is the  -dimensional geodesic ball of radius
-dimensional geodesic ball of radius  centered
centered  in
in  (
( , resp.).
, resp.).
Proof.
Let  .
.  is a convex set,
is a convex set,  , and the same argument holds as in Proposition 2.6; we have
, and the same argument holds as in Proposition 2.6; we have

Denote the volume forms on  and
and  by
by  and
and  , respectively. Then we have
, respectively. Then we have

It follows that

Hence we have

In the above inequality we used the fact that  and
and  on
on  Therefore we obtain
Therefore we obtain

This completes the proof for 
The similar argument applies to 
Remark 2.10.
The classical monotonicity of a minimal submanifold in the Euclidean or hyperbolic space can be found in [6, 8, 9].
In case  lies on a geodesic sphere,
lies on a geodesic sphere,  automatically satisfies the radially connectivity. In this case, the relative isoperimetric inequality can be extended to the hyperbolic space, and to a minimal submanifold case (not necessarily a minimal surface case). More precisely, we have the following theorem.
automatically satisfies the radially connectivity. In this case, the relative isoperimetric inequality can be extended to the hyperbolic space, and to a minimal submanifold case (not necessarily a minimal surface case). More precisely, we have the following theorem.
Theorem 2.11.
Let  be a closed convex set in
be a closed convex set in  or
or  and let
and let  be an
be an  -dimensional compact minimal submanifold of
-dimensional compact minimal submanifold of  or
or  satisfying that
satisfying that  is orthogonal to
is orthogonal to  along
along  . Assume that
. Assume that  lies on a geodesic sphere centered at a point
lies on a geodesic sphere centered at a point  and that
and that  is the distance in
is the distance in  or
or  from
from  . Furthermore, in case of
. Furthermore, in case of  , assume that
, assume that  . Then
. Then

where equality holds if and only if  is an
is an  -dimensional totally geodesic half-ball centered at
-dimensional totally geodesic half-ball centered at  .
.
Proof.
Assume that  is a minimal submanifold in
is a minimal submanifold in  with
with  lying on a geodesic sphere. Let
lying on a geodesic sphere. Let  be the radius of the geodesic sphere. Since
be the radius of the geodesic sphere. Since  is a convex set and the same argument holds as in Proposition 2.6, then
is a convex set and the same argument holds as in Proposition 2.6, then

By Proposition 2.9,  Hence
Hence

and so the desired inequality follows. Equality holds if and only if  is a cone with density at the center equal to
is a cone with density at the center equal to  , or equivalently,
, or equivalently,  is a totally geodesic half-ball in
is a totally geodesic half-ball in  . A similar proof holds for
. A similar proof holds for 
3. Weak Relative Isoperimetric Inequalities in a Riemannian Manifold
The results in Section 2 are sharp but those require some extra assumptions on their boundary. And the results are concerned with the modified volume. In this section, by contrast, we obtain weak relative isoperimetric inequality which holds for any minimal surface and holds for the usual volume.
From now on, we denote  as
as  and
and  as
as  for simplicity.
for simplicity.
Theorem 3.1.
Let  be a closed convex set in a complete simply connected Riemannian manifold
be a closed convex set in a complete simply connected Riemannian manifold  of sectional curvature bounded above by a constant
of sectional curvature bounded above by a constant  . Assume that
. Assume that  is a compact minimal surface in the outside of
is a compact minimal surface in the outside of  such that
such that  is orthogonal to
is orthogonal to  along
along  . In case of
. In case of  , one assumes that
, one assumes that  . Then one has
. Then one has

To prove the above theorem, we begin with the following lemmas on the Laplacian on functions of distance.
Lemma 3.2.
Let  be an m-dimensional compact minimal submanifold in a simply connected Riemannian manifold
be an m-dimensional compact minimal submanifold in a simply connected Riemannian manifold  of sectional curvature bounded above by a constant
of sectional curvature bounded above by a constant  . Define
. Define  for a fixed point
for a fixed point  .
.
(a)If  , then one has
, then one has  on
on  .
.
(b)If  , then one has
, then one has  on
on  .
.
(c)If  , then one has
, then one has  on
on  .
.
Proof.
Lemma 3.3.
Let  be a compact minimal surface satisfying the same assumptions as in Theorem 3.1. Define
be a compact minimal surface satisfying the same assumptions as in Theorem 3.1. Define  for any
for any  .
.
(a)If  , then one has on
, then one has on 
(1)
(b)If  , then one has on
, then one has on 
(2) ,
,
(3) .
.
(c)If  , then one has on
, then one has on 
(4) if
if  ,
,
(5) if
if  .
.
Proof.
For  , using Lemma 3.2(c), we have
, using Lemma 3.2(c), we have

Near  ,
,  can be identified with totally geodesic half-sphere with constant sectional curvature
can be identified with totally geodesic half-sphere with constant sectional curvature  . Since
. Since  is a fundamental solution of Laplacian on
is a fundamental solution of Laplacian on  ,
,  . Hence we obtain (4).
. Hence we obtain (4).
Next for (5) we compute

Note that

which proves (5) by (4).
For  , using Lemma 3.2(a) and
, using Lemma 3.2(a) and  being a fundamental solution of Laplacian on
being a fundamental solution of Laplacian on  , we get (1).
, we get (1).
For  , using Lemma 3.2(b) and
, using Lemma 3.2(b) and  being a fundamental solution of Laplacian on
being a fundamental solution of Laplacian on  , we get (2). By similar argument as before, we get (3).
, we get (2). By similar argument as before, we get (3).
Proof of Theorem 3.1.
-
(i)
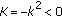 . Let
. Let  be the distance from
be the distance from 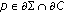 to
to  . Integrating Lemma 3.3(3) over
. Integrating Lemma 3.3(3) over 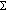 for the point
for the point 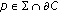 , we get
, we get 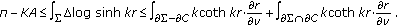 (3.5)
(3.5)
Since the same argument holds as in Proposition 2.6, we have

This inequality holds for all  , and we can integrate it over
, and we can integrate it over  and apply Fubini's theorem to obtain
and apply Fubini's theorem to obtain

By Lemma 3.2(b) and convexity of  , we get
, we get

-
(ii)
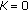 . Integrate Lemma 3.3(1) twice and apply Lemma 3.2(a) as in (i).
. Integrate Lemma 3.3(1) twice and apply Lemma 3.2(a) as in (i). -
(iii)
 . Integrate Lemma 3.3(5) twice and apply Lemma 3.2(c) as in (i).
. Integrate Lemma 3.3(5) twice and apply Lemma 3.2(c) as in (i).
This completes the proof.
References
Choe J, Gulliver R: The sharp isoperimetric inequality for minimal surfaces with radially connected boundary in hyperbolic space. Inventiones Mathematicae 1992, 109(3):495–503.
Kim I: Relative isoperimetric inequality and linear isoperimetric inequality for minimal submanifolds. Manuscripta Mathematica 1998, 97(3):343–352. 10.1007/s002290050107
Choe J, Ghomi M, Ritore M: The relative isoperimetric inequality outside convex domains
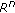 in . Calculus of Variations and Partial Differential Equations 2007, 29(4):421–429. 10.1007/s00526-006-0027-z
in . Calculus of Variations and Partial Differential Equations 2007, 29(4):421–429. 10.1007/s00526-006-0027-zChoe J, Ritore M: The relative isoperimetric inequality in Cartan-Hadamard 3-manifolds. Journal für die Reine und Angewandte Mathematik 2007, 605: 179–191.
Bandle C: Isoperimetric Inequalities and Applications. Pitman, Boston, Mass, USA; 1980:x+228.
Choe J, Gulliver R: Isoperimetric inequalities on minimal submanifolds of space forms. Manuscripta Mathematica 1992, 77(2–3):169–189.
Choe J: The isoperimetric inequality for a minimal surface with radially connected boundary. Annali della Scuola Normale Superiore di Pisa. Classe di Scienze 1990, 17(4):583–593.
Anderson MT: Complete minimal varieties in hyperbolic space. Inventiones Mathematicae 1982, 69(3):477–494. 10.1007/BF01389365
Simon L: Lectures on Geometric Measure Theory, Proceedings of the Centre for Mathematical Analysis. Volume 3. Australian National University, Canberra, Australia; 1983.
Choe J: The isoperimetric inequality for minimal surfaces in a Riemannian manifold. Journal für die Reine und Angewandte Mathematik 1999, 506: 205–214.
Acknowledgment
This work was supported in part by KRF-2007-313-C00057.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Pyo, J. Relative Isoperimetric Inequality for Minimal Submanifolds in a Riemannian Manifold. J Inequal Appl 2010, 758623 (2010). https://doi.org/10.1155/2010/758623
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/758623
 is an
is an 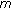 -dimensional minimal submanifold or a cone, and
-dimensional minimal submanifold or a cone, and  is the distance in
is the distance in 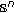 from a fixed point, then
from a fixed point, then 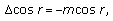
 is an
is an  -dimensional minimal submanifold or a cone. Then
-dimensional minimal submanifold or a cone. Then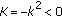 . Let
. Let  be the distance from
be the distance from 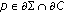 to
to  . Integrating Lemma 3.3(3) over
. Integrating Lemma 3.3(3) over 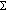 for the point
for the point 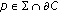 , we get
, we get 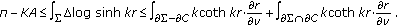
 . Integrate Lemma 3.3(1) twice and apply Lemma 3.2(a) as in (i).
. Integrate Lemma 3.3(1) twice and apply Lemma 3.2(a) as in (i). . Integrate Lemma 3.3(5) twice and apply Lemma 3.2(c) as in (i).
. Integrate Lemma 3.3(5) twice and apply Lemma 3.2(c) as in (i). in . Calculus of Variations and Partial Differential Equations 2007, 29(4):421–429. 10.1007/s00526-006-0027-z
in . Calculus of Variations and Partial Differential Equations 2007, 29(4):421–429. 10.1007/s00526-006-0027-z