- Research Article
- Open access
- Published:
Random Stability of an Additive-Quadratic-Quartic Functional Equation
Journal of Inequalities and Applications volume 2010, Article number: 754210 (2010)
Abstract
Using the fixed point method, we prove the generalized Hyers-Ulam stability of the following additive-quadratic-quartic functional equation  in complete random normed spaces.
in complete random normed spaces.
1. Introduction
The stability problem of functional equations originated from a question of Ulam [1] concerning the stability of group homomorphisms. Hyers [2] gave a first affirmative partial answer to the question of Ulam for Banach spaces. Hyers' theorem was generalized by Aoki [3] for additive mappings and by Th. M. Rassias [4] for linear mappings by considering an unbounded Cauchy difference. The paper of Th. M. Rassias [4] has provided a lot of influence in the development of what we call generalized Hyers-Ulam stability or as Hyers-Ulam-Rassias stability of functional equations. A generalization of the Th. M. Rassias theorem was obtained by G vru
vru a [5] by replacing the unbounded Cauchy difference by a general control function in the spirit of Th. M. Rassias' approach.
a [5] by replacing the unbounded Cauchy difference by a general control function in the spirit of Th. M. Rassias' approach.
The functional equation

is called a quadratic functional equation. In particular, every solution of the quadratic functional equation is said to be a quadratic mapping. A generalized Hyers-Ulam stability problem for the quadratic functional equation was proved by Skof [6] for mappings  , where
, where  is a normed space and
is a normed space and  is a Banach space. Cholewa [7] noticed that the theorem of Skof is still true if the relevant domain
is a Banach space. Cholewa [7] noticed that the theorem of Skof is still true if the relevant domain  is replaced by an Abelian group. Czerwik [8] proved the generalized Hyers-Ulam stability of the quadratic functional equation. The stability problems of several functional equations have been extensively investigated by a number of authors and there are many interesting results concerning this problem (see [4, 9–26]).
is replaced by an Abelian group. Czerwik [8] proved the generalized Hyers-Ulam stability of the quadratic functional equation. The stability problems of several functional equations have been extensively investigated by a number of authors and there are many interesting results concerning this problem (see [4, 9–26]).
In [27], Lee et al. considered the following quartic functional equation

It is easy to show that the function  satisfies the functional equation (1.2), which is called a quartic functional equation and every solution of the quartic functional equation is said to be a quartic mapping.
satisfies the functional equation (1.2), which is called a quartic functional equation and every solution of the quartic functional equation is said to be a quartic mapping.
Let  be a set. A function
be a set. A function  is called a generalized metric on
is called a generalized metric on  if
if  satisfies
satisfies
(1) if and only if
if and only if  ,
,
(2) for all
for all 
(3) for all
for all  .
.
We recall a fundamental result in fixed point theory.
Let  be a complete generalized metric space and let
be a complete generalized metric space and let  be a strictly contractive mapping with Lipschitz constant
be a strictly contractive mapping with Lipschitz constant  . Then for each given element
. Then for each given element  , either
, either

for all nonnegative integers  or there exists a positive integer
or there exists a positive integer  such that
such that
(1)
(2)the sequence  converges to a fixed point
converges to a fixed point  of
of  ,
,
(3) is the unique fixed point of
is the unique fixed point of  in the set
in the set  ,
,
(4) for all
for all  .
.
In 1996, Isac and Th. M. Rassias [30] were the first to provide applications of stability theory of functional equations for the proof of new fixed point theorems with applications. By using fixed point methods, the stability problems of several functional equations have been extensively investigated by a number of authors (see [31–36]).
2. Preliminaries
In the sequel we adopt the usual terminology, notations and conventions of the theory of random normed spaces, as in [37–41]. Throughout this paper,  is the space of all probability distribution functions that is, the space of all mappings
is the space of all probability distribution functions that is, the space of all mappings  , such that
, such that  is left-continuous, non-decreasing on
is left-continuous, non-decreasing on  ,
,  and
and  .
.  is a subset of
is a subset of  consising of all functions
consising of all functions  for which
for which  , where
, where  denotes the left limit of the function
denotes the left limit of the function  at the point
at the point  , that is,
, that is,  . The space
. The space  is partially ordered by the usual point-wise ordering of functions, that is,
is partially ordered by the usual point-wise ordering of functions, that is,  if and only if
if and only if  for all
for all  in
in  . The maximal element for
. The maximal element for  in this order is the distribution function
in this order is the distribution function  given by
given by

Definition 2.1 ([40]).
A mapping  is a continuous triangular norm (briefly, a
is a continuous triangular norm (briefly, a  -norm) if
-norm) if  satisfies the following conditions:
satisfies the following conditions:
(a) is commutative and associative;
is commutative and associative;
(b) is continuous;
is continuous;
(c) for all
for all  ;
;
(d) whenever
whenever  and
and  for all
for all  .
.
Typical examples of continuous  -norms are
-norms are  ,
,  and
and  (the
(the  ukasiewicz
ukasiewicz  -norm).
-norm).
Recall (see [42, 43]) that if  is a
is a  -norm and
-norm and  is a given sequence of numbers in
is a given sequence of numbers in  ,
,  is defined recurrently by
is defined recurrently by  and
and  for
for  .
.  is defined as
is defined as  .
.
It is known ([43]) that for the  ukasiewicz
ukasiewicz  -norm the following implication holds:
-norm the following implication holds:

Definition 2.2 ([41]).
A Random Normed space (briefly, RN-space) is a triple  , where
, where  is a vector space,
is a vector space,  is a continuous
is a continuous  -norm, and
-norm, and  is a mapping from
is a mapping from  into
into  such that, the following conditions hold:
such that, the following conditions hold:
(RN1) for all
for all  if and only if
if and only if  ;
;
(RN2) for all
for all  ,
,  ;
;
(RN3) for all
for all  and
and  .
.
Definition 2.3.
Let  be a RN-space.
be a RN-space.
(1)A sequence  in
in  is said to be convergent to
is said to be convergent to  in
in  if, for every
if, for every  and
and  , there exists positive integer
, there exists positive integer  such that
such that  whenever
whenever  .
.
(2)A sequence  in
in  is called Cauchy if, for every
is called Cauchy if, for every  and
and  , there exists positive integer
, there exists positive integer  such that
such that  whenever
whenever  .
.
(3)A RN-space  is said to be complete if and only if every Cauchy sequence in
is said to be complete if and only if every Cauchy sequence in  is convergent to a point in
is convergent to a point in  . A complete RN-space is said to be random Banach space.
. A complete RN-space is said to be random Banach space.
Theorem 2.4 ([40]).
If  is a RN-space and
is a RN-space and  is a sequence such that
is a sequence such that  , then
, then  almost everywhere.
almost everywhere.
The theory of random normed spaces (RN-spaces) is important as a generalization of deterministic result of linear normed spaces and also in the study of random operator equations. The RN-spaces may also provide us the appropriate tools to study the geometry of nuclear physics and have important application in quantum particle physics. The generalized Hyers-Ulam stability of different functional equations in random normed spaces, RN-spaces and fuzzy normed spaces has been recently studied in, Alsina [44], Mirmostafaee, Mirzavaziri and Moslehian [33, 45–47], Mihe and Radu [38, 39, 48, 49], Mihe
and Radu [38, 39, 48, 49], Mihe , Saadati and Vaezpour [50, 51], Baktash et al. [52] and Saadati et al. [53].
, Saadati and Vaezpour [50, 51], Baktash et al. [52] and Saadati et al. [53].
3. Generalized Hyers-Ulam Stability of the Functional Equation 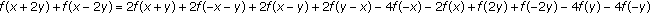 : An Odd Case
: An Odd Case
One can easily show that an odd mapping  satisfies
satisfies  if and only if the odd mapping mapping
if and only if the odd mapping mapping  is an additive mapping, that is,
is an additive mapping, that is,

One can easily show that an even mapping  satisfies
satisfies  if and only if the even mapping
if and only if the even mapping  is a quadratic-quartic mapping, that is,
is a quadratic-quartic mapping, that is,

It was shown in [54, Lemma  ] that
] that  and
and  are quartic and quadratic, respectively, and that
are quartic and quadratic, respectively, and that  .
.
For a given mapping  , we define
, we define

for all  .
.
Using the fixed point method, we prove the generalized Hyers-Ulam stability of the functional equation  in complete RN-spaces: an odd case.
in complete RN-spaces: an odd case.
Theorem 3.1.
Let  be a linear space,
be a linear space,  be a complete RN-space and
be a complete RN-space and  be a mapping from
be a mapping from  to
to 
 such that, for some
such that, for some  ,
,

Let  be an odd mapping satisfying
be an odd mapping satisfying

for all  and all
and all  . Then
. Then

exists for each  and defines a unique additive mapping
and defines a unique additive mapping  such that
such that

for all  and all
and all  .
.
Proof.
Letting  in (3.5), we get
in (3.5), we get

for all  and all
and all  .
.
Consider the set

and introduce the generalized metric on  :
:

where, as usual,  . It is easy to show that
. It is easy to show that  is complete. (See the proof of Lemma
is complete. (See the proof of Lemma  in [38].)
in [38].)
Now we consider the linear mapping  such that
such that

for all  and we prove that
and we prove that  is a strictly contractive mapping with the Lipschitz constant
is a strictly contractive mapping with the Lipschitz constant  .
.
Let  be given such that
be given such that  . Then
. Then

for all  and all
and all  . Hence
. Hence

for all  and all
and all  . So
. So  implies that
implies that  . This means that
. This means that

for all  .
.
It follows from (3.8) that

for all  and all
and all  . So
. So

By Theorem 1.1, there exists a mapping  satisfying the following:
satisfying the following:
-
(1)
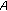 is a fixed point of
is a fixed point of 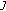 , that is,
, that is, 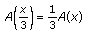 (3.17)
(3.17)
for all  . The mapping
. The mapping  is a unique fixed point of
is a unique fixed point of  in the set
in the set

This implies that  is a unique mapping satisfying (3.17) such that there exists a
is a unique mapping satisfying (3.17) such that there exists a  satisfying
satisfying

for all  and all
and all  ;
;
-
(2)
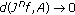 as
as 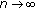 . This implies the equality
. This implies the equality 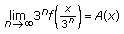 (3.20)
(3.20)
for all  . Since
. Since  is odd,
is odd,  is an odd mapping;
is an odd mapping;
-
(3)
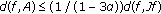 with
with 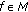 , which implies the inequality
, which implies the inequality 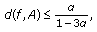 (3.21)
(3.21)
from which it follows

This implies that the inequality (3.7) holds.
Now, we have,

for all  , all
, all  and all
and all  .
.
So, we obtain by (3.4)

for all  , all
, all  and all
and all  .
.
Since  for all
for all  and all
and all  , by Theorem 2.4, we deduce that
, by Theorem 2.4, we deduce that

for all  and all
and all  . Thus the mapping
. Thus the mapping  is additive, as desired.
is additive, as desired.
Corollary 3.2.
Let  and let
and let  be a real number with
be a real number with  . Let
. Let  be a normed vector space with norm
be a normed vector space with norm  . Let
. Let  be an odd mapping satisfying
be an odd mapping satisfying

for all  and all
and all  . Then
. Then

exists for each  and defines an additive mapping
and defines an additive mapping  such that
such that

for all  and all
and all  .
.
Proof.
The proof follows from Theorem 3.1 by taking

for all  . Then we can choose
. Then we can choose  and we get the desired result.
and we get the desired result.
Similarly, we can obtain the following. We will omit the proof.
Theorem 3.3.
Let  be a linear space,
be a linear space,  be a complete RN-space and
be a complete RN-space and  be a mapping from
be a mapping from  to
to  (
( is denoted by
is denoted by  )such that, for some
)such that, for some  ,
,

Let  be an odd mapping satisfying (3.5). Then
be an odd mapping satisfying (3.5). Then

exists for each  and defines a unique additive mapping
and defines a unique additive mapping  such that
such that

for all  and all
and all  .
.
Corollary 3.4.
Let  and let
and let  be a real number with
be a real number with  . Let
. Let  be a normed vector space with norm
be a normed vector space with norm  . Let
. Let  be an odd mapping satisfying (3.26). Then
be an odd mapping satisfying (3.26). Then

exists for each  and defines a unique additive mapping
and defines a unique additive mapping  such that
such that

for all  and all
and all  .
.
Proof.
The proof follows from Theorem 3.3 by taking

for all  . Then we can choose
. Then we can choose  and we get the desired result.
and we get the desired result.
4. Generalized Hyers-Ulam Stability of the Functional Equation 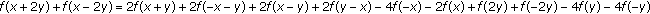 : An Even Case
: An Even Case
Using the fixed point method, we prove the generalized Hyers-Ulam stability of the functional equation  in random Banach spaces: an even case.
in random Banach spaces: an even case.
Theorem 4.1.
Let  be a linear space, let
be a linear space, let  be a complete RN-space and
be a complete RN-space and  be a mapping from
be a mapping from  to
to  (
( is denoted by
is denoted by  )such that, for some
)such that, for some  ,
,

Let  be an even mapping satisfying
be an even mapping satisfying  and (3.5). Then
and (3.5). Then

exists for each  and defines a quartic mapping
and defines a quartic mapping  such that
such that

for all  and all
and all  .
.
Proof.
Letting  in (3.5), we get
in (3.5), we get

for all  and all
and all  .
.
Replacing  by
by  in (3.5), we get
in (3.5), we get

for all  and all
and all  .
.
By (4.4) and (4.5),

for all  and all
and all  . Letting
. Letting  for all
for all  , we get
, we get

for all  and all
and all  .
.
Let  be the generalized metric space defined in the proof of Theorem 3.1.
be the generalized metric space defined in the proof of Theorem 3.1.
Now we consider the linear mapping  such that
such that

for all  . It is easy to see that
. It is easy to see that  is a strictly contractive self-mapping on
is a strictly contractive self-mapping on  with the Lipschitz constant
with the Lipschitz constant  .
.
It follows from (4.7) that

for all  and all
and all  . So
. So

By Theorem 1.1, there exists a mapping  satisfying the following:
satisfying the following:
-
(1)
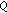 is a fixed point of
is a fixed point of  , that is,
, that is,  (4.11)
(4.11)
for all  . Since
. Since  is even with
is even with  ,
,  is an even mapping with
is an even mapping with  . The mapping
. The mapping  is a unique fixed point of
is a unique fixed point of  in the set
in the set

This implies that  is a unique mapping satisfying (4.11) such that there exists a
is a unique mapping satisfying (4.11) such that there exists a  satisfying
satisfying

for all  and all
and all  ;
;
-
(2)
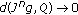 as
as 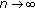 . This implies the equality
. This implies the equality  (4.14)
(4.14)
for all  ;
;
-
(3)
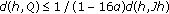 for every
for every 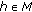 , which implies the inequality
, which implies the inequality  (4.15)
(4.15)
This implies that the inequality (4.3) holds.
Proceeding as in the proof of Theorem 3.1, we obtain that the mapping  satisfies
satisfies  .
.
Now, we have

for every  . Since the mapping
. Since the mapping  is quartic (see [54, Lemma
is quartic (see [54, Lemma  ]), we get that the mapping
]), we get that the mapping  is quartic.
is quartic.
Corollary 4.2.
Let  and let
and let  be a real number with
be a real number with  . Let
. Let  be a normed vector space with norm
be a normed vector space with norm  . Let
. Let  be an even mapping satisfying
be an even mapping satisfying  and (3.26). Then
and (3.26). Then

exists for each  and defines a quartic mapping
and defines a quartic mapping  such that
such that

for all  and all
and all  .
.
Proof.
The proof follows from Theorem 3.1 by taking

for all  . Then we can choose
. Then we can choose  and we get the desired result.
and we get the desired result.
Similarly, we can obtain the following. We will omit the proof.
Theorem 4.3.
Let  be a linear space,
be a linear space,  be a complete RN-space and
be a complete RN-space and  be a mapping from
be a mapping from  to
to  (
( is denoted by
is denoted by  )such that, for some
)such that, for some  ,
,

Let  be an even mapping satisfying
be an even mapping satisfying  and (3.5). Then
and (3.5). Then

exists for each  and defines a quartic mapping
and defines a quartic mapping  such that
such that

for all  and all
and all  .
.
Corollary 4.4.
Let  and let
and let  be a real number with
be a real number with  . Let
. Let  be a normed vector space with norm
be a normed vector space with norm  . Let
. Let  be an even mapping satisfying
be an even mapping satisfying  and (3.26). Then
and (3.26). Then

exists for each  and defines a quartic mapping
and defines a quartic mapping  such that
such that

for all  and all
and all  .
.
Proof.
The proof follows from Theorem 3.3 by taking

for all  . Then we can choose
. Then we can choose  and we get the desired result.
and we get the desired result.
Theorem 4.5.
Let  be a linear space,
be a linear space,  be a complete RN-space and
be a complete RN-space and  be a mapping from
be a mapping from  to
to  (
( is denoted by
is denoted by  )such that, for some
)such that, for some  ,
,

Let  be an even mapping satisfying
be an even mapping satisfying  and (3.5). Then
and (3.5). Then

exists for each  and defines a quadratic mapping
and defines a quadratic mapping  such that
such that

for all  and all
and all  .
.
Proof.
Let  be the generalized metric space defined in the proof of Theorem 4.1.
be the generalized metric space defined in the proof of Theorem 4.1.
Letting  for all
for all  in (4.6), we get
in (4.6), we get

for all  and all
and all  .
.
It is easy to see that the linear mapping  such that
such that

for all  , is a strictly contractive self-mapping with the Lipschitz constant
, is a strictly contractive self-mapping with the Lipschitz constant  .
.
It follows from (4.29) that

for all  and all
and all  . So
. So

By Theorem 1.1, there exists a mapping  satisfying the following.
satisfying the following.
-
(1)
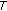 is a fixed point of
is a fixed point of 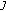 , that is,
, that is, 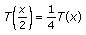 (4.33)
(4.33)
for all  . Since
. Since  is even with
is even with  ,
,  is an even mapping with
is an even mapping with  . The mapping
. The mapping  is a unique fixed point of
is a unique fixed point of  in the set
in the set

This implies that  is a unique mapping satisfying (4.33) such that there exists a
is a unique mapping satisfying (4.33) such that there exists a  satisfying
satisfying

for all  and all
and all  ;
;
-
(2)
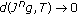 as
as 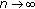 . This implies the equality
. This implies the equality  (4.36)
(4.36)
for all  ;
;
-
(3)
 for each
for each 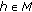 , which implies the inequality
, which implies the inequality 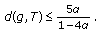 (4.37)
(4.37)
This implies that the inequality (4.28) holds.
Proceeding as in the proof of Theorem 4.1, we obtain that the mapping  satisfies
satisfies  .
.
Now, we have

for every  . Since the mapping
. Since the mapping  is quadratic (see [54, Lemma
is quadratic (see [54, Lemma  ]), we get that the mapping
]), we get that the mapping  is quadratic.
is quadratic.
Corollary 4.6.
Let  and let
and let  be a real number with
be a real number with  . Let
. Let  be a normed vector space with norm
be a normed vector space with norm  . Let
. Let  be an even mapping satisfying
be an even mapping satisfying  and (3.26). Then
and (3.26). Then

exists for each  and defines a quadratic mapping
and defines a quadratic mapping  such that
such that

for all  and all
and all  .
.
Proof.
The proof follows from Theorem 4.5 by taking

for all  . Then we can choose
. Then we can choose  and we get the desired result.
and we get the desired result.
Similarly, we can obtain the following. We will omit the proof.
Theorem 4.7.
Let  be a linear space,
be a linear space,  be a complete RN-space and
be a complete RN-space and  be a mapping from
be a mapping from  to
to  (
( is denoted by
is denoted by  ) such that, for some
) such that, for some  ,
,

Let  be an even mapping satisfying
be an even mapping satisfying  and (3.5). Then
and (3.5). Then

exists for each  and defines a quadratic mapping
and defines a quadratic mapping  such that
such that

for all  and all
and all  .
.
Corollary 4.8.
Let  and let
and let  be a real number with
be a real number with  . Let
. Let  be a normed vector space with norm
be a normed vector space with norm  . Let
. Let  be an even mapping satisfying
be an even mapping satisfying  and (3.26). Then
and (3.26). Then

exists for each  and defines a quadratic mapping
and defines a quadratic mapping  such that
such that

for all  and all
and all  .
.
Proof.
The proof follows from Theorem 4.7 by taking

for all  . Then we can choose
. Then we can choose  and we get the desired result.
and we get the desired result.
References
Ulam SM: A Collection of Mathematical Problems, Interscience Tracts in Pure and Applied Mathematics, no. 8. Interscience, New York, NY, USA; 1960:xiii+150.
Hyers DH: On the stability of the linear functional equation. Proceedings of the National Academy of Sciences of the United States of America 1941, 27: 222–224. 10.1073/pnas.27.4.222
Aoki T: On the stability of the linear transformation in Banach spaces. Journal of the Mathematical Society of Japan 1950, 2: 64–66. 10.2969/jmsj/00210064
Rassias ThM: On the stability of the linear mapping in Banach spaces. Proceedings of the American Mathematical Society 1978, 72(2):297–300. 10.1090/S0002-9939-1978-0507327-1
Găvruţa P: A generalization of the Hyers-Ulam-Rassias stability of approximately additive mappings. Journal of Mathematical Analysis and Applications 1994, 184(3):431–436. 10.1006/jmaa.1994.1211
Skof F: Proprieta' locali e approssimazione di operatori. Rendiconti del Seminario Matematico e Fisico di Milano 1983, 53: 113–129. 10.1007/BF02924890
Cholewa PW: Remarks on the stability of functional equations. Aequationes Mathematicae 1984, 27(1–2):76–86.
Czerwik S: On the stability of the quadratic mapping in normed spaces. Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg 1992, 62: 59–64. 10.1007/BF02941618
Eshaghi-Gordji M, Kaboli-Gharetapeh S, Park C, Zolfaghri S: Stability of an additive-cubic-quartic functional equation. Advances in Difference Equations 2009, 2009:-20.
Hyers DH, Isac G, Rassias ThM: Stability of Functional Equations in Several Variables, Progress in Nonlinear Differential Equations and Their Applications, 34. Birkhäuser, Boston, Mass, USA; 1998:vi+313.
Jun K-W, Kim H-M: The generalized Hyers-Ulam-Rassias stability of a cubic functional equation. Journal of Mathematical Analysis and Applications 2002, 274(2):267–278.
Jung S: Hyers-Ulam-Rassias Stability of Functional Equations in Mathematical Analysis. Hadronic Press, Palm Harbor, Fla, USA; 2001:ix+256.
Park C: Hyers-Ulam-Rassias stability of homomorphisms in quasi-Banach algebras. Bulletin des Sciences Mathématiques 2008, 132(2):87–96.
Park C, Cui J: Generalized stability of
 -ternary quadratic mappings. Abstract and Applied Analysis 2007, 2007:-6.
-ternary quadratic mappings. Abstract and Applied Analysis 2007, 2007:-6.Park C, Najati A: Homomorphisms and derivations in
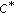 -algebras. Abstract and Applied Analysis 2007, 2007:-12.
-algebras. Abstract and Applied Analysis 2007, 2007:-12.Rassias JM: On approximation of approximately linear mappings by linear mappings. Bulletin des Sciences Mathématiques 1984, 108(4):445–446.
Rassias JM: Refined Hyers-Ulam approximation of approximately Jensen type mappings. Bulletin des Sciences Mathématiques 2007, 131(1):89–98.
Rassias JM, Rassias MJ: Asymptotic behavior of alternative Jensen and Jensen type functional equations. Bulletin des Sciences Mathématiques 2005, 129(7):545–558.
Rassias ThM: Problem 16; 2, report of the 27th International Symposium on Functional Equations. Aequationes Mathematicae 39(2–3):292–293.
Rassias ThM: On the stability of the quadratic functional equation and its applications. Studia Universitatis Babeş-Bolyai. Mathematica 1998, 43(3):89–124.
Rassias ThM: The problem of S. M. Ulam for approximately multiplicative mappings. Journal of Mathematical Analysis and Applications 2000, 246(2):352–378. 10.1006/jmaa.2000.6788
Rassias ThM: On the stability of functional equations in Banach spaces. Journal of Mathematical Analysis and Applications 2000, 251(1):264–284. 10.1006/jmaa.2000.7046
Rassias ThM: On the stability of functional equations and a problem of Ulam. Acta Applicandae Mathematicae 2000, 62(1):23–130. 10.1023/A:1006499223572
Rassias ThM, Šemrl P: On the behavior of mappings which do not satisfy Hyers-Ulam stability. Proceedings of the American Mathematical Society 1992, 114(4):989–993. 10.1090/S0002-9939-1992-1059634-1
Rassias ThM, Šemrl P: On the Hyers-Ulam stability of linear mappings. Journal of Mathematical Analysis and Applications 1993, 173(2):325–338. 10.1006/jmaa.1993.1070
Rassias ThM, Shibata K: Variational problem of some quadratic functionals in complex analysis. Journal of Mathematical Analysis and Applications 1998, 228(1):234–253. 10.1006/jmaa.1998.6129
Lee SH, Im SM, Hwang IS: Quartic functional equations. Journal of Mathematical Analysis and Applications 2005, 307(2):387–394. 10.1016/j.jmaa.2004.12.062
Cădariu L, Radu V: Fixed points and the stability of Jensen's functional equation. Journal of Inequalities in Pure and Applied Mathematics 2003., 4(1, article 4):
Diaz JB, Margolis B: A fixed point theorem of the alternative, for contractions on a generalized complete metric space. Bulletin of the American Mathematical Society 1968, 74: 305–309. 10.1090/S0002-9904-1968-11933-0
Isac G, Rassias ThM: Stability of
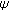 -additive mappings: applications to nonlinear analysis. International Journal of Mathematics and Mathematical Sciences 1996, 19(2):219–228. 10.1155/S0161171296000324
-additive mappings: applications to nonlinear analysis. International Journal of Mathematics and Mathematical Sciences 1996, 19(2):219–228. 10.1155/S0161171296000324Cădariu L, Radu V: On the stability of the Cauchy functional equation: a fixed point approach. In Iteration Theory, Grazer Mathematische Berichte. Volume 346. Karl-Franzens-Universitaet Graz, Graz, Austria; 2004:43–52.
Cădariu L, Radu V: Fixed point methods for the generalized stability of functional equations in a single variable. Fixed Point Theory and Applications 2008, 2008:-15.
Mirzavaziri M, Moslehian MS: A fixed point approach to stability of a quadratic equation. Bulletin of the Brazilian Mathematical Society 2006, 37(3):361–376. 10.1007/s00574-006-0016-z
Park C: Fixed points and Hyers-Ulam-Rassias stability of Cauchy-Jensen functional equations in Banach algebras. Fixed Point Theory and Applications 2007, 2007:-15.
Park C: Generalized Hyers-Ulam stability of quadratic functional equations: a fixed point approach. Fixed Point Theory and Applications 2008, 2008:-9.
Radu V: The fixed point alternative and the stability of functional equations. Fixed Point Theory 2003, 4(1):91–96.
Chang S, Cho Y, Kang SM: Nonlinear Operator Theory in Probabilistic Metric Spaces. Nova Science, Huntington, NY, USA; 2001:x+338.
Miheţ D, Radu V: On the stability of the additive Cauchy functional equation in random normed spaces. Journal of Mathematical Analysis and Applications 2008, 343(1):567–572.
Miheţ D: Fuzzy stability of additive mappings in non-Archimedean fuzzy normed spaces. Fuzzy Sets and Systems. In press
Schweizer B, Sklar A: Probabilistic Metric Spaces, North-Holland Series in Probability and Applied Mathematics. North-Holland, New York, NY, USA; 1983:xvi+275.
Šerstnev AN: On the concept of a stochastic normalized space. Doklady Akademii Nauk SSSR 1963, 149: 280–283.
Hadžić O, Pap E: Fixed Point Theory in Probabilistic Metric Spaces, Mathematics and Its Applications. Volume 536. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2001:x+273.
Hadžić O, Pap E, Budinčević M: Countable extension of triangular norms and their applications to the fixed point theory in probabilistic metric spaces. Kybernetika 2002, 38(3):363–382.
Alsina C: On the stability of a functional equation arising in probabilistic normed spaces. In General Inequalities, Internationale Schriftenreihe zur Numerischen Mathematik. Volume 80. Birkhäuser, Basel, Switzerland; 1987:263–271.
Mirmostafaee AK, Mirzavaziri M, Moslehian MS: Fuzzy stability of the Jensen functional equation. Fuzzy Sets and Systems 2008, 159(6):730–738. 10.1016/j.fss.2007.07.011
Mirmostafaee AK, Moslehian MS: Fuzzy versions of Hyers-Ulam-Rassias theorem. Fuzzy Sets and Systems 2008, 159(6):720–729. 10.1016/j.fss.2007.09.016
Mirmostafaee AK, Moslehian MS: Fuzzy approximately cubic mappings. Information Sciences 2008, 178(19):3791–3798. 10.1016/j.ins.2008.05.032
Miheţ D: The probabilistic stability for a functional equation in a single variable. Acta Mathematica Hungarica 2009, 123(3):249–256. 10.1007/s10474-008-8101-y
Miheţ D: The fixed point method for fuzzy stability of the Jensen functional equation. Fuzzy Sets and Systems 2009, 160(11):1663–1667. 10.1016/j.fss.2008.06.014
Miheţ D, Saadati R, Vaezpour SM: The stability of the quartic functional equation in random normed spaces. Acta Applicandae Mathematicae. In press
Miheţ D, Saadati R, Vaezpour SM: The stability of an additive functional equation in Menger probabilistic -normed spaces. Mathematica Slovaca. In press
Baktash E, Cho YJ, Jalili M, Saadati R, Vaezpour SM: On the stability of cubic mappings and quadratic mappings in random normed spaces. Journal of Inequalities and Applications 2008, 2008:-11.
Saadati R, Vaezpour SM, Cho YJ: A note to paper "On the stability of cubic mappings and quartic mappings in random normed spaces". Journal of Inequalities and Applications 2009, 2009:-6.
Eshaghi-Gordji M, Abbaszadeh S, Park C: On the stability of a generalized quadratic and quartic type functional equation in quasi-Banach spaces. Journal of Inequalities and Applications 2009, 2009:-26.
Acknowledgments
The authors would like to thank referees for giving useful suggestions for the improvement of this paper. The first author is supported by Islamic Azad University-Ayatollah Amoli Branch, Amol, Iran. The second author was supported by the Korea Research Foundation Grant funded by the Korean Government (KRF-2008-313-C00050) and the third author was supported by Basic Science Research Program through the National Research Foundation of Korea funded by the Ministry of Education, Science and Technology (NRF-2009-0070788). The fourth author is supported by Università degli Studi di Palermo, R.S. ex 60%.
Author information
Authors and Affiliations
Corresponding authors
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Mohamadi, M., Cho, Y., Park, C. et al. Random Stability of an Additive-Quadratic-Quartic Functional Equation. J Inequal Appl 2010, 754210 (2010). https://doi.org/10.1155/2010/754210
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/754210
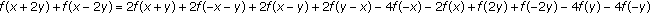 : An Odd Case
: An Odd Case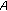 is a fixed point of
is a fixed point of 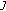 , that is,
, that is, 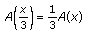
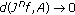 as
as 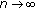 . This implies the equality
. This implies the equality 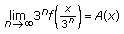
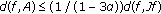 with
with 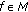 , which implies the inequality
, which implies the inequality 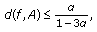
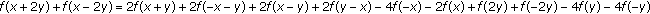 : An Even Case
: An Even Case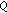 is a fixed point of
is a fixed point of  , that is,
, that is, 
 as
as  . This implies the equality
. This implies the equality 
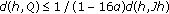 for every
for every 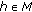 , which implies the inequality
, which implies the inequality 
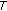 is a fixed point of
is a fixed point of 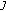 , that is,
, that is, 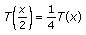
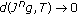 as
as 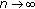 . This implies the equality
. This implies the equality 
 for each
for each 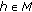 , which implies the inequality
, which implies the inequality 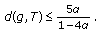
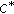 -ternary quadratic mappings. Abstract and Applied Analysis 2007, 2007:-6.
-ternary quadratic mappings. Abstract and Applied Analysis 2007, 2007:-6.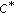 -algebras. Abstract and Applied Analysis 2007, 2007:-12.
-algebras. Abstract and Applied Analysis 2007, 2007:-12.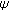 -additive mappings: applications to nonlinear analysis. International Journal of Mathematics and Mathematical Sciences 1996, 19(2):219–228. 10.1155/S0161171296000324
-additive mappings: applications to nonlinear analysis. International Journal of Mathematics and Mathematical Sciences 1996, 19(2):219–228. 10.1155/S0161171296000324