- Research Article
- Open access
- Published:
Common Fixed Points of Weakly Contractive and Strongly Expansive Mappings in Topological Spaces
Journal of Inequalities and Applications volume 2010, Article number: 746045 (2010)
Abstract
Using the notion of weakly  -contractive mappings, we prove several new common fixed point theorems for commuting as well as noncommuting mappings on a topological space X. By analogy, we obtain a common fixed point theorem of mappings which are strongly
-contractive mappings, we prove several new common fixed point theorems for commuting as well as noncommuting mappings on a topological space X. By analogy, we obtain a common fixed point theorem of mappings which are strongly  -expansive on X.
-expansive on X.
1. Introduction
It is well known that if  is a compact metric space and
is a compact metric space and  is a weakly contractive mapping (see Section 2 for the definition), then
is a weakly contractive mapping (see Section 2 for the definition), then  has a fixed point in
has a fixed point in  (see [1, p. 17]). In late sixties, Furi and Vignoli [2] extended this result to
(see [1, p. 17]). In late sixties, Furi and Vignoli [2] extended this result to  -condensing mappings acting on a bounded complete metric space (see [3] for the definition). A generalized version of Furi-Vignoli's theorem using the notion of weakly
-condensing mappings acting on a bounded complete metric space (see [3] for the definition). A generalized version of Furi-Vignoli's theorem using the notion of weakly  -contractive mappings acting on a topological space was proved in [4] (see also [5]).
-contractive mappings acting on a topological space was proved in [4] (see also [5]).
On the other hand, in [6] while examining KKM maps, the authors introduced a new concept of lower (upper) semicontinuous function (see Definition 2.1, Section 2) which is more general than the classical one. In [7], the authors used this definition of lower semicontinuity to redefine weakly  -contractive mappings and strongly
-contractive mappings and strongly  -expansive mappings (see Definition 2.6, Section 2 ) to formulate and prove several results for fixed points.
-expansive mappings (see Definition 2.6, Section 2 ) to formulate and prove several results for fixed points.
In this article, we have used the notions of weakly  -contractive mappings (
-contractive mappings ( where
where  is a topological space) to prove a version of the above-mentioned fixed point theorem [7, Theorem
is a topological space) to prove a version of the above-mentioned fixed point theorem [7, Theorem  ] for common fixed points (see Theorem 3.1). We also prove a common fixed point theorem under the assumption that certain iteration of the mappings in question is weakly
] for common fixed points (see Theorem 3.1). We also prove a common fixed point theorem under the assumption that certain iteration of the mappings in question is weakly  -contractive. As a corollary to this fact, we get an extension (to common fixed points) of [7, Theorem
-contractive. As a corollary to this fact, we get an extension (to common fixed points) of [7, Theorem  ] for Banach spaces with a quasimodulus endowed with a suitable transitive binary relation. The most interesting result of this section is Theorem 3.8 wherein the strongly
] for Banach spaces with a quasimodulus endowed with a suitable transitive binary relation. The most interesting result of this section is Theorem 3.8 wherein the strongly  -expansive condition on
-expansive condition on  (with some other conditions) implies that
(with some other conditions) implies that  and
and  have a unique common fixed point.
have a unique common fixed point.
In Section 4, we define a new class of noncommuting self-maps and prove some common fixed point results for this new class of mappings.
2. Preliminaries
Definition 2.1 (see [6]).
Let  be a topological space. A function
be a topological space. A function 
 is said to be lower semi-continuous from above (lsca) at
is said to be lower semi-continuous from above (lsca) at  if for any net
if for any net  convergent to
convergent to  with
with

we have

A function 
 is said to be lsca if it is lsca at every
is said to be lsca if it is lsca at every 
Example 2.2.
-
(i)
Let
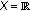 . Define
. Define 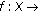
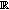 by
by 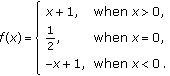 (2.3)
(2.3)
Let  be a sequence of nonnegative terms such that
be a sequence of nonnegative terms such that  converges to
converges to  . Then
. Then

Similarly, if  is a sequence in
is a sequence in  of negative terms such that
of negative terms such that  converges to
converges to  , then
, then

Thus,  is lsca at
is lsca at 
-
(ii)
 Every lower semi-continuous function is lsca but not conversely. One can check that the function
Every lower semi-continuous function is lsca but not conversely. One can check that the function 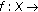
 with
with 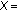
 defined below is lsca at
defined below is lsca at  but is not lower semi-continuous at
but is not lower semi-continuous at  :
: 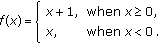 (2.6)
(2.6)
The following lemmas state some properties of lsca mappings. The first one is an analogue of Weierstrass boundedness theorem and the second one is about the composition of a continuous function and a function lsca.
Lemma 2.3 (see [6]).
Let  be a compact topological space and
be a compact topological space and  a function lsca. Then there exists
a function lsca. Then there exists  such that
such that 
Lemma 2.4 (see [7]).
Let  be a topological space and
be a topological space and  a continuous function. If
a continuous function. If is a function lsca, then the composition function
is a function lsca, then the composition function  is also lsca.
is also lsca.
Proof.
Fix 
 and consider a net
and consider a net  in
in  convergent to
convergent to  such that
such that

Set  and
and  Then since
Then since  is continuous,
is continuous, 
 and
and  lsca implies that
lsca implies that

with  for
for  Thus
Thus 

 and
and  is lsca.
is lsca.
Remark 2.5 (see [6]).
Let  be topological space. Let
be topological space. Let  be a continuous function and
be a continuous function and  lsca. Then
lsca. Then  defined by
defined by  is also lsca. For this, let
is also lsca. For this, let  be a net in
be a net in  convergent to
convergent to  Since
Since  is continuous,
is continuous,  Suppose that
Suppose that

Then since  is lsca, we have
is lsca, we have

Definition 2.6 (see [7]).
Let  be a topological space and
be a topological space and 
 be lsca. The mapping
be lsca. The mapping 
 is said to be
is said to be
(i)weakly  -contractive if
-contractive if  for all
for all  such that
such that 
(ii)strongly  -expansive if
-expansive if  for all
for all  such that
such that 
If  is a metric space with metric
is a metric space with metric  and
and  , then we call
, then we call  respectively, weakly contractive and strongly expansive.
respectively, weakly contractive and strongly expansive.
Let  . The set of fixed points of
. The set of fixed points of  (resp.,
(resp.,  ) is denoted by
) is denoted by  (resp.,
(resp.,  ). A point
). A point  is a coincidence point (common fixed point) of
is a coincidence point (common fixed point) of  and
and  if
if 
 . The set of coincidence points of
. The set of coincidence points of  and
and  is denoted by
is denoted by  Maps
Maps  are called (1) commuting if
are called (1) commuting if  for all
for all  , (2) weakly compatible [8] if they commute at their coincidence points, that is, if
, (2) weakly compatible [8] if they commute at their coincidence points, that is, if  whenever
whenever  , and (3) occasionally weakly compatible [9] if
, and (3) occasionally weakly compatible [9] if  for some
for some 
3. Common Fixed Point Theorems for Commuting Maps
In this section we extend some results in [7] to the setting of two mappings having a unique common fixed point.
Theorem 3.1.
Let  be a topological space,
be a topological space,  , and
, and  self-mappings such that for every countable set
self-mappings such that for every countable set 

and  ,
,  commute on
commute on  If
If
(i) is continuous and weakly
is continuous and weakly  -contractive or
-contractive or
(ii) is continuous and weakly
is continuous and weakly  -contractive with
-contractive with  ,
,
then  and
and  have a unique common fixed point.
have a unique common fixed point.
Proof.
Let  and define the sequence
and define the sequence  by setting
by setting  for
for  Let
Let  Then
Then

so by hypothesis  is compact. Define
is compact. Define  by
by

Now if  or
or  is continuous and since
is continuous and since  is lsca, then by Remark 2.5,
is lsca, then by Remark 2.5,  is lsca. So by Lemma 2.3,
is lsca. So by Lemma 2.3,  has a minimum at, say,
has a minimum at, say, 
(i Suppose that
Suppose that is continuous and weakly
is continuous and weakly -contractive. Then
-contractive. Then  as
as  is continuous. Now observe that if
is continuous. Now observe that if 
 is continuous, and
is continuous, and  , then
, then  We show that
We show that  Suppose that
Suppose that  ; then
; then

a contradiction to the minimality of  at
at  Having
Having  one can see that
one can see that  Indeed, if
Indeed, if  then we have
then we have

a contradiction.
-
(ii)
Suppose that
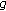 is continuous and weakly
is continuous and weakly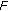 -contractive with
-contractive with  . Then
. Then 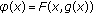 as
as  is continuous. Put
is continuous. Put  ; then
; then 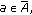
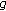 is continuous, and
is continuous, and 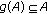 implies that
implies that 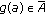 . We claim that
. We claim that 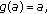 for otherwise we will have
for otherwise we will have  (3.6)
(3.6)
which is a contradiction. Hence the claim follows.
Now suppose that  then we have
then we have

a contradiction, hence 
In both cases, uniqueness follows from the contractive conditions: suppose there exists  such that
such that  Then we have
Then we have

which is false. Thus  and
and  have a unique common fixed point.
have a unique common fixed point.
If  , then Theorem 3.1(i) reduces to [7, Theorem
, then Theorem 3.1(i) reduces to [7, Theorem  ].
].
Corollary 3.2 (see [7, Theorem  ]).
]).
Let  be a topological space,
be a topological space,  , and
, and  continuous and weakly
continuous and weakly  -contractive. If the implication
-contractive. If the implication 

holds for every countable set  then
then  has a unique fixed point.
has a unique fixed point.
Example 3.3.
Let 
 be the Banach space of all null real sequences. Define
be the Banach space of all null real sequences. Define

Let  and
and  a sequence such that
a sequence such that

with  as
as  Define the mappings
Define the mappings  by
by

where 
 and
and 
 are such that for
are such that for  ,
,


and for 

We verify the hypothesis of Theorem 3.1.
(i)Observe that  and
and  are, clearly, continuous by their definition.
are, clearly, continuous by their definition.
(ii)For  we have
we have

Since the sequences  and
and  are null sequences, there exists
are null sequences, there exists  such that
such that

Hence

This implies that  and
and  are weakly contractive. Thus
are weakly contractive. Thus  and
and  are continuous and weakly contractive. Next suppose that for any countable set
are continuous and weakly contractive. Next suppose that for any countable set  we have
we have

then by the definition of  , we can consider
, we can consider  Hence closure of
Hence closure of  being closed subset of a compact set is compact. Also
being closed subset of a compact set is compact. Also

So by Theorem 3.1,  and
and  have a unique common fixed point.
have a unique common fixed point.
Corollary 3.4.
Let ( be a metric space,
be a metric space,  , and
, and  self-mappings such that for every countable set
self-mappings such that for every countable set 

and  ,
,  commute on
commute on  If
If
(i) is continuous and weakly contractive or
is continuous and weakly contractive or
(ii) is continuous and weakly contractive with
is continuous and weakly contractive with  ,
,
then  and
and  have a unique common fixed point.
have a unique common fixed point.
Proof.
It is immediate from Theorem 3.1 with  .
.
Corollary 3.5.
Let  be a compact metric space,
be a compact metric space,  , and
, and  self-mappings such that for every countable set
self-mappings such that for every countable set 

and  ,
,  commute on
commute on  If
If
(i) is continuous and weakly contractive or
is continuous and weakly contractive or
(ii) is continuous and weakly
is continuous and weakly  -contractive with
-contractive with 
then  and
and  have a unique common fixed point.
have a unique common fixed point.
Proof.
It is immediate from Theorem 3.1.
Theorem 3.6.
Let  be a topological space,
be a topological space,  , and
, and  self-mappings such that for every countable set
self-mappings such that for every countable set 
-
(1)
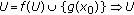 is relatively compact;
is relatively compact; -
(2)
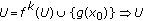 is relatively compact for some
is relatively compact for some 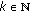 ;
; -
(3)
 is relatively compact for some
is relatively compact for some 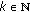 .
.
And  ,
,  commute on
commute on  Further, if
Further, if

then  and
and  have a unique common fixed point.
have a unique common fixed point.
Proof.
Part (3): we proceed as in Theorem 3.1. Let  for some
for some  and define the sequence
and define the sequence  by setting
by setting  for
for  Let
Let  Then
Then

so by hypothesis (3),  is compact. Define
is compact. Define  by
by

Now since  is lsca and if
is lsca and if  or
or  is continuous, then by Remark 2.5
is continuous, then by Remark 2.5  would be lsca and hence by Lemma 2.3,
would be lsca and hence by Lemma 2.3,  would have a minimum, say, at
would have a minimum, say, at 
(i)Suppose that is continuous and
is continuous and weakly
weakly -contractive. Then
-contractive. Then  as
as  is continuous. Now observe that
is continuous. Now observe that 
 is continuous, and
is continuous, and  implies that
implies that  is continuous and
is continuous and  and so
and so  for some
for some  . We show that
. We show that  . Suppose that
. Suppose that  for any
for any  , then
, then

a contradiction to the minimality of  at
at  Therefore,
Therefore,  for some
for some  . One can check that
. One can check that  . Suppose that
. Suppose that  , then we have
, then we have

a contradiction. Thus  is a common fixed point of
is a common fixed point of  and
and  and hence of
and hence of  and
and 
-
(ii)
Suppose that
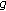 is continuous and
is continuous and weakly
weakly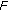 -contractive with
-contractive with 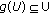 . Then
. Then 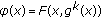 as
as  is continuous. Put
is continuous. Put 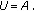 Then
Then 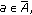
 continuous and
continuous and 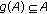 imply that
imply that 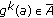 . We claim that
. We claim that  for otherwise we will have
for otherwise we will have 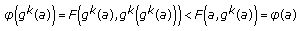 (3.28)
(3.28)
which is a contradiction. Hence the claim follows.
Now suppose that  then we have
then we have

a contradiction, hence  Thus
Thus  is a common fixed point of
is a common fixed point of  and
and  and hence of
and hence of  and
and 
Now we establish the uniqueness of  Suppose there exists
Suppose there exists  such that
such that  for some
for some  . Now if
. Now if  is continuous and
is continuous and  is weakly
is weakly  - contractive, then we have
- contractive, then we have

and if  is continuous and
is continuous and  is weakly
is weakly  - contractive, then we have
- contractive, then we have

which is false. Thus  and
and  have a unique common fixed point which obviously is a unique common fixed point of
have a unique common fixed point which obviously is a unique common fixed point of  and
and  .
.
Part (2). The conclusion follows if we set  in part (3).
in part (3).
Part (1). The conclusion follows if we set  and
and  in part (3).
in part (3).
A nice consequence of Theorem 3.6 is the following theorem where  is taken as a Banach space equipped with a transitive binary relation.
is taken as a Banach space equipped with a transitive binary relation.
Theorem 3.7.
Let 
 be a Banach space with a transitive binary relation
be a Banach space with a transitive binary relation  such that
such that  for
for 

 with
with  Suppose, further, that the mappings
Suppose, further, that the mappings  are such that the following conditions are satisfied:
are such that the following conditions are satisfied:
(i) and
and  for all
for all 

(ii) then
then 
(iii)A is bounded linear operator and  for some
for some  and for all
and for all  such that
such that  with
with 
If either

for all  with
with 
 commuting on
commuting on  and if one of the conditions, (1)–(3), of Theorem 3.6 holds, then
and if one of the conditions, (1)–(3), of Theorem 3.6 holds, then  and
and  have a unique common fixed point.
have a unique common fixed point.
Proof.
-
(a)
Suppose that
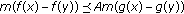 for all
for all  with
with  commuting on
commuting on  and
and  is contractive
is contractive Then we have
Then we have 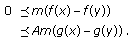 (3.33)
(3.33)
Next

Therefore, after  -steps,
-steps,  , we get
, we get

Hence,

So  is weakly contractive. Since
is weakly contractive. Since  is continuous (as
is continuous (as  is bounded and
is bounded and  contractive) by Theorem 3.6,
contractive) by Theorem 3.6,  and
and  have a unique common fixed point.
have a unique common fixed point.
 b
b Suppose that
Suppose that  and
and  is contractive for all
is contractive for all  with
with  commuting on
commuting on  and
and  being contractive
being contractive The proof now follows if we mutually interchange
The proof now follows if we mutually interchange  in (a) above
in (a) above
Theorem 3.8.
Let  be a topological space,
be a topological space,  with
with  closed and
closed and  Let
Let  be mappings such that for every countable set
be mappings such that for every countable set 

and  ,
,  commute on
commute on  If
If  is a homeomorphism and strongly
is a homeomorphism and strongly  -expansive, then
-expansive, then  and
and  have a unique common fixed point.
have a unique common fixed point.
Proof.
Suppose that  is a homeomorphism and strongly
is a homeomorphism and strongly  -expansive. Let
-expansive. Let  with
with  Then there exists
Then there exists  such that
such that  and
and  or
or  and
and  Since
Since  is strongly
is strongly  -expansive, we have
-expansive, we have

or

So  is a weakly
is a weakly  -contractive mapping. Choose any countable subset
-contractive mapping. Choose any countable subset  of
of  and set
and set  Suppose that
Suppose that

Then  for some
for some  and we get
and we get

So by hypothesis  is compact and since
is compact and since  is a homeomorphism,
is a homeomorphism, 
 is compact. Since
is compact. Since  for every
for every  and
and  , we have
, we have

for every  Thus
Thus

and  for every
for every  Since
Since  is continuous and weakly
is continuous and weakly  -contractive, by Theorem 3.1, the mappings
-contractive, by Theorem 3.1, the mappings  and
and  have a unique common fixed point, say,
have a unique common fixed point, say,  . Since
. Since  implies that
implies that  so
so  is a unique common fixed point of
is a unique common fixed point of  and
and 
The following example illustrates Theorem 3.8.
Example 3.9.
Let  with the River metric
with the River metric  defined by
defined by

where  ,
,  , and
, and  denotes the Euclidean metric on
denotes the Euclidean metric on  Then
Then  is a topological space with a topology induced by the metric
is a topological space with a topology induced by the metric  . Consider the sets
. Consider the sets  defined by
defined by

Let the mappings  be defined by
be defined by  and
and  for
for  Then
Then  is clearly a homeomorphism and for an arbitrary countable subset
is clearly a homeomorphism and for an arbitrary countable subset  of
of  and
and  ,
,

If and only if  Indeed, if
Indeed, if  such that
such that  , then
, then

Further,  for every
for every  Set
Set  where
where  is the Radial metric defined by
is the Radial metric defined by

and  ;
;  Now for
Now for  since
since

 is strongly
is strongly  -expansive. Also
-expansive. Also  is lower semi-continuous and hence lsca. Thus all the conditions of Theorem 3.8 are satisfied and
is lower semi-continuous and hence lsca. Thus all the conditions of Theorem 3.8 are satisfied and  and
and  have a unique common fixed point.
have a unique common fixed point.
4. Occasionally Banach Operator Pair and Weak F-Contractions
In this section, we define a new class of noncommuting self-maps and prove some common fixed point results for this new class of maps.
The pair  is called a Banach operator pair [10] if the set
is called a Banach operator pair [10] if the set  is
is  -invariant, namely,
-invariant, namely,  . Obviously, commuting pair
. Obviously, commuting pair  is a Banach operator pair but converse is not true, in general; see [10–13]. If
is a Banach operator pair but converse is not true, in general; see [10–13]. If  is a Banach operator pair, then
is a Banach operator pair, then  need not be a Banach operator pair.
need not be a Banach operator pair.
Definition 4.1.
The pair  is called occasionally Banach operator pair if
is called occasionally Banach operator pair if

Clearly, Banach operator pair (BOP)  is occasionally Banach operator pair (OBOP) but not conversely, in general.
is occasionally Banach operator pair (OBOP) but not conversely, in general.
Example 4.2.
Let  with usual norm. Define
with usual norm. Define  by
by  and
and  , for
, for  and
and  .
.  and
and  . Obviously
. Obviously  is OBOP but not BOP as
is OBOP but not BOP as  . Further,
. Further,  is not weakly compatible and hence not commuting.
is not weakly compatible and hence not commuting.
Example 4.3.
Let  with usual norm and
with usual norm and  . Define
. Define  by
by


Here  and
and  implies that
implies that  is not Banach operator pair. Similarly,
is not Banach operator pair. Similarly,  is not Banach operator pair. Further,
is not Banach operator pair. Further,

imply that  is OBOP. Further, note that
is OBOP. Further, note that  and
and  . Hence
. Hence  is not occasionally weakly compatible pair.
is not occasionally weakly compatible pair.
Definition 4.4.
Let  be a nonempty set and
be a nonempty set and  be a mapping such that
be a mapping such that

For a space  satisfying (4.5) and
satisfying (4.5) and  the diameter of
the diameter of  is defined by
is defined by

Here we extend this concept to the space  satisfying condition (4.5).
satisfying condition (4.5).
Definition 4.5.
Let  be a space satisfying (4.5). The pair
be a space satisfying (4.5). The pair  is called occasionally Banach operator pair on
is called occasionally Banach operator pair on  iff there is a point
iff there is a point  in
in  such that
such that  and
and

Theorem 4.6.
Let  be a topological space,
be a topological space,  , and
, and  self-mappings such that for every countable set
self-mappings such that for every countable set 

If  is continuous and weakly
is continuous and weakly  -contractive,
-contractive,  satisfies condition (4.5), and the pair
satisfies condition (4.5), and the pair  is occasionally Banach operator pair, then
is occasionally Banach operator pair, then  and
and  have a unique common fixed point.
have a unique common fixed point.
Proof.
By Corollary 3.2,  is a singleton. Let
is a singleton. Let  . Then, by our hypothesis,
. Then, by our hypothesis,

Therefore,  . That is,
. That is,  is unique common fixed point of
is unique common fixed point of  and
and  .
.
Corollary 4.7.
Let ( be a metric space,
be a metric space,  , and
, and  self-mappings such that for every countable set
self-mappings such that for every countable set 

If  is continuous and weakly contractive and the pair
is continuous and weakly contractive and the pair  is occasionally Banach operator pair, then
is occasionally Banach operator pair, then  and
and  have a unique common fixed point.
have a unique common fixed point.
Proof.
It is immediate from Theorem 4.6 with  .
.
Corollary 4.8.
Let  be a compact metric space,
be a compact metric space,  , and
, and  self-mappings such that for every countable set
self-mappings such that for every countable set 

If  is continuous and weakly contractive and the pair
is continuous and weakly contractive and the pair  is occasionally Banach operator pair, then
is occasionally Banach operator pair, then  and
and  have a unique common fixed point.
have a unique common fixed point.
Proof.
It is immediate from Theorem 4.6.
Theorem 4.6 holds for a Banach operator pair without condition (4.5) as follows.
Theorem 4.9.
Let  be a topological space,
be a topological space,  , and
, and  self-mappings such that for every countable set
self-mappings such that for every countable set 

If  is continuous and weakly
is continuous and weakly  -contractive and the pair
-contractive and the pair  is a Banach operator pair, then
is a Banach operator pair, then  and
and  have a unique common fixed point.
have a unique common fixed point.
Proof.
By Corollary 3.2,  is a singleton. Let
is a singleton. Let  . As
. As  is a Banach operator pair, by definition
is a Banach operator pair, by definition  . Thus
. Thus  and hence
and hence  . That is,
. That is,  is unique common fixed point of
is unique common fixed point of  and
and  .
.
Corollary 4.10.
Let ( be a metric space,
be a metric space,  , and
, and  self-mappings such that for every countable set
self-mappings such that for every countable set 

If  is continuous and weakly contractive and the pair
is continuous and weakly contractive and the pair  is a Banach operator pair, then
is a Banach operator pair, then  and
and  have a unique common fixed point.
have a unique common fixed point.
References
Dugundji J, Granas A: Fixed Point Theory, Vol. 1. PWN, Warsaw, Poland; 1982:209.
Furi M, Vignoli A: A fixed point theorem in complete metric spaces. Bolletino della Unione Matematica Italiana 1969, 4: 505–509.
Bugajewski D: Some remarks on Kuratowski's measure of noncompactness in vector spaces with a metric. Commentationes Mathematicae 1992, 32: 5–9.
Bugajewski D: Fixed point theorems in locally convex spaces. Acta Mathematica Hungarica 2003, 98(4):345–355. 10.1023/A:1022842429470
Ćirić LB: Coincidence and fixed points for maps on topological spaces. Topology and Its Applications 2007, 154(17):3100–3106. 10.1016/j.topol.2007.08.004
Chen YQ, Cho YJ, Kim JK, Lee BS: Note on KKM maps and applications. Fixed Point Theory and Applications 2006, 2006:-9.
Bugajewski D, Kasprzak P: Fixed point theorems for weakly
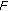 -contractive and strongly
-contractive and strongly 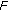 -expansive mappings. Journal of Mathematical Analysis and Applications 2009, 359(1):126–134. 10.1016/j.jmaa.2009.05.024
-expansive mappings. Journal of Mathematical Analysis and Applications 2009, 359(1):126–134. 10.1016/j.jmaa.2009.05.024Jungck G: Common fixed points for noncontinuous nonself maps on nonmetric spaces. Far East Journal of Mathematical Sciences 1996, 4(2):199–215.
Jungck G, Rhoades BE: Fixed point theorems for occasionally weakly compatible mappings. Fixed Point Theory 2006, 7(2):287–296.
Chen J, Li Z: Common fixed-points for Banach operator pairs in best approximation. Journal of Mathematical Analysis and Applications 2007, 336(2):1466–1475. 10.1016/j.jmaa.2007.01.064
Hussain N: Common fixed points in best approximation for Banach operator pairs with Ćirić type
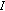 -contractions. Journal of Mathematical Analysis and Applications 2008, 338(2):1351–1363. 10.1016/j.jmaa.2007.06.008
-contractions. Journal of Mathematical Analysis and Applications 2008, 338(2):1351–1363. 10.1016/j.jmaa.2007.06.008Hussain N, Cho YJ: Weak contractions, common fixed points, and invariant approximations. Journal of Inequalities and Applications 2009, 2009:-10.
Pathak HK, Hussain N: Common fixed points for Banach operator pairs with applications. Nonlinear Analysis 2008, 69: 2788–2802. 10.1016/j.na.2007.08.051
Acknowledgments
N. Hussain thanks the Deanship of Scientific Research, King Abdulaziz University for the support of the Research Project no. (3-74/430). A. R. Khan is grateful to the King Fahd University of Petroleum  Minerals and SABIC for the support of the Research Project no. SB
Minerals and SABIC for the support of the Research Project no. SB
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Shah, M.H., Hussain, N. & Khan, A.R. Common Fixed Points of Weakly Contractive and Strongly Expansive Mappings in Topological Spaces. J Inequal Appl 2010, 746045 (2010). https://doi.org/10.1155/2010/746045
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/746045
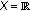 . Define
. Define 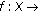
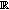 by
by 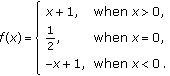
 Every lower semi-continuous function is lsca but not conversely. One can check that the function
Every lower semi-continuous function is lsca but not conversely. One can check that the function 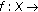
 with
with 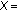
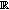 defined below is lsca at
defined below is lsca at  but is not lower semi-continuous at
but is not lower semi-continuous at  :
: 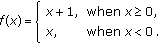
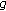 is continuous and weakly
is continuous and weakly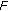 -contractive with
-contractive with  . Then
. Then 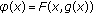 as
as  is continuous. Put
is continuous. Put  ; then
; then 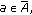
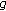 is continuous, and
is continuous, and 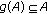 implies that
implies that 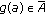 . We claim that
. We claim that 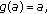 for otherwise we will have
for otherwise we will have 
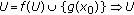 is relatively compact;
is relatively compact;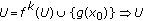 is relatively compact for some
is relatively compact for some 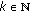 ;
; is relatively compact for some
is relatively compact for some 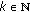 .
.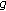 is continuous and
is continuous and weakly
weakly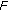 -contractive with
-contractive with 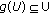 . Then
. Then 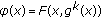 as
as  is continuous. Put
is continuous. Put 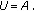 Then
Then 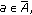
 continuous and
continuous and 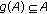 imply that
imply that 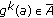 . We claim that
. We claim that  for otherwise we will have
for otherwise we will have 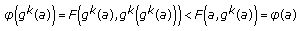
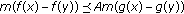 for all
for all  with
with 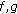 commuting on
commuting on 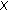 and
and  is contractive
is contractive Then we have
Then we have 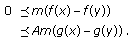
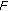 -contractive and strongly
-contractive and strongly 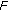 -expansive mappings. Journal of Mathematical Analysis and Applications 2009, 359(1):126–134. 10.1016/j.jmaa.2009.05.024
-expansive mappings. Journal of Mathematical Analysis and Applications 2009, 359(1):126–134. 10.1016/j.jmaa.2009.05.024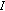 -contractions. Journal of Mathematical Analysis and Applications 2008, 338(2):1351–1363. 10.1016/j.jmaa.2007.06.008
-contractions. Journal of Mathematical Analysis and Applications 2008, 338(2):1351–1363. 10.1016/j.jmaa.2007.06.008