- Research Article
- Open access
- Published:
A Generalized Nonlinear Random Equations with Random Fuzzy Mappings in Uniformly Smooth Banach Spaces
Journal of Inequalities and Applications volume 2010, Article number: 728452 (2010)
Abstract
We introduce and study the general nonlinear random  -accretive equations with random fuzzy mappings. By using the resolvent technique for the
-accretive equations with random fuzzy mappings. By using the resolvent technique for the  -accretive operators, we prove the existence theorems and convergence theorems of the generalized random iterative algorithm for this nonlinear random equations with random fuzzy mappings in
-accretive operators, we prove the existence theorems and convergence theorems of the generalized random iterative algorithm for this nonlinear random equations with random fuzzy mappings in  -uniformly smooth Banach spaces. Our result in this paper improves and generalizes some known corresponding results in the literature.
-uniformly smooth Banach spaces. Our result in this paper improves and generalizes some known corresponding results in the literature.
1. Introduction
Fuzzy Set Theory was formalised by Professor Lofti Zadeh at the University of California in 1965 with a view to reconcile mathematical modeling and human knowledge in the engineering sciences. The concept of fuzzy sets is incredible wide range of areas, from mathematics and logics to traditional and advanced engineering methodologies. Applications are found in many contexts, from medicine to finance, from human factors to consumer products, and from vehicle control to computational linguistics.
Random variational inequality theories is an important part of random function analysis. These topics have attracted many scholars and exports due to the extensive applications of the random problems (see, e.g., [1–17]). In 1997, Huang [3] first introduced the concept of random fuzzy mapping and studied the random nonlinear quasicomplementarity problem for random fuzzy mappings. Further, Huang studied the random generalized nonlinear variational inclusions for random fuzzy mappings in Hilbert spaces. Ahmad and Bazán [18] studied a class of random generalized nonlinear mixed variational inclusions for random fuzzy mappings and constructed an iterative algorithm for solving such random problems.
Very recently, Lan et al. [11], introduced and studied a class of general nonlinear random multivalued operator equations involving generalized  -accretive mappings in Banach spaces and an iterative algorithm with errors for this nonlinear random multivalued operator equations.
-accretive mappings in Banach spaces and an iterative algorithm with errors for this nonlinear random multivalued operator equations.
Inspired and motivated by recent works in these fields (see [2, 13, 14, 18–29]), in this paper, we introduce and study a class of general nonlinear random equations with random fuzzy mappings in Banach spaces. By using Chang's lemma and the resolvent operator technique for  -accretive mapping. We prove the existence and convergence theorems of the generalized random iterative algorithm for this nonlinear random equations with random fuzzy mappings in
-accretive mapping. We prove the existence and convergence theorems of the generalized random iterative algorithm for this nonlinear random equations with random fuzzy mappings in  -uniformly smooth Banach spaces. Our results improve and extend the corresponding results of recent works.
-uniformly smooth Banach spaces. Our results improve and extend the corresponding results of recent works.
2. Preliminaries
Throughout this paper, let  be a complete
be a complete  -finite measure space and
-finite measure space and  be a separable real Banach space. We denote by
be a separable real Banach space. We denote by  ,
,  and
and  the class of Borel
the class of Borel  -fields in
-fields in  , the inner product and the norm on
, the inner product and the norm on  , respectively. In the sequel, we denote
, respectively. In the sequel, we denote  ,
,  and
and  by
by  ,
,  is nonempty, bounded and closed} and the Hausdorff metric on
is nonempty, bounded and closed} and the Hausdorff metric on  , respectively.
, respectively.
Next, we will use the following definitions and lemmas.
Definition 2.1.
An operator  is said to be measurable if, for any
is said to be measurable if, for any  ,
,  .
.
Definition 2.2.
A operator  is called a random operator if for any
is called a random operator if for any  ,
,  is measurable. A random operator
is measurable. A random operator  is said to be continuous (resp. linear, bounded) if for any
is said to be continuous (resp. linear, bounded) if for any  , the operator
, the operator  is continuous (resp. linear, bounded).
is continuous (resp. linear, bounded).
Similarly, we can define a random operator  . We will write
. We will write  and
and  for all
for all  and
and  .
.
It is well known that a measurable operator is necessarily a random operator.
Definition 2.3.
A multivalued operator  is said to be measurable if, for any
is said to be measurable if, for any  ,
,  .
.
Definition 2.4.
A operator  is called a measurable selection of a multivalued measurable operator
is called a measurable selection of a multivalued measurable operator  if
if  is measurable and for any
is measurable and for any  ,
,  .
.
Lemma 2.5 (see [19]).
Let  be a
be a  -continuous random multivalued operator. Then, for any measurable operator
-continuous random multivalued operator. Then, for any measurable operator  , the multivalued operator
, the multivalued operator  is measurable.
is measurable.
Lemma 2.6 (see [19]).
Let  be two measurable multivalued operators,
be two measurable multivalued operators,  be a constant and
be a constant and  be a measurable selection of
be a measurable selection of  . Then there exists a measurable selection
. Then there exists a measurable selection  of
of  such that, for any
such that, for any  ,
,

Definition 2.7.
A multivalued operator  is called a random multivalued operator if, for any
is called a random multivalued operator if, for any  ,
,  is measurable. A random multivalued operator
is measurable. A random multivalued operator  is said to be
is said to be  -continuous if, for any
-continuous if, for any  ,
,  is continuous in
is continuous in  , where
, where  is the Hausdorff metric on
is the Hausdorff metric on  defined as follows: for any given
defined as follows: for any given  ,
,

Let  be the family of all fuzzy sets over
be the family of all fuzzy sets over  . A mapping
. A mapping  is called a fuzzy mapping over
is called a fuzzy mapping over  .
.
If  is a fuzzy mapping over
is a fuzzy mapping over  , then
, then  (denoted by
(denoted by  ) is fuzzy set on
) is fuzzy set on  , and
, and  is the membership degree of the point
is the membership degree of the point  in
in  . Let
. Let  ,
,  . Then the set
. Then the set

is called a  -cut set of fuzzy set
-cut set of fuzzy set  .
.
(i)A fuzzy mapping  is called measurable if, for any given
is called measurable if, for any given  ,
,  is a measurable multivalued mapping.
is a measurable multivalued mapping.
(ii)A fuzzy mapping  is called a random fuzzy mapping if, for any
is called a random fuzzy mapping if, for any  ,
,  is a measurable fuzzy mapping.
is a measurable fuzzy mapping.
Let  be three random fuzzy mappings satisfying the following condition (C): there exists three mappings
be three random fuzzy mappings satisfying the following condition (C): there exists three mappings  , such that
, such that

By using the random fuzzy mappings  ,
,  and
and  , we can define the three multivalued mappings
, we can define the three multivalued mappings  ,
,  and
and  as follows, respectively.
as follows, respectively.

It means that

It easy to see that  ,
,  and
and  are the random multivalued mappings. We call
are the random multivalued mappings. We call  ,
,  and
and  are random multivalued mappings induced by fuzzy mappings
are random multivalued mappings induced by fuzzy mappings  and
and  , respectively.
, respectively.
Suppose that  and
and  with
with  ,
,  and
and  be two single-valued mappings. Let
be two single-valued mappings. Let  be three random fuzzy mappings satisfying the condition (C). Given mappings
be three random fuzzy mappings satisfying the condition (C). Given mappings  . Now, we consider the following problem:
. Now, we consider the following problem:
Find measurable mappings  such that for all
such that for all  ,
,  ,
,  ,
,  ,
,  and
and

The problem (2.7) is called random variational inclusion problem for random fuzzy mappings in Banach spaces. The set of measurable mappings  is called a random solution of (2.7).
is called a random solution of (2.7).
Some special cases of (2.7):
-
(1)
If
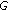 is a single-valued operator,
is a single-valued operator, 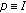 , where
, where  is the identity mapping and
is the identity mapping and 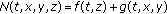 for all
for all 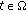 and
and 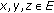 , then (2.7) is equivalent to finding
, then (2.7) is equivalent to finding 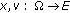 such that
such that 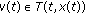 and
and 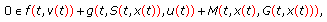 (2.8)
(2.8)
for all  and
and  . The problem (2.8) was considered and studied by Agarwal et al. [1], when
. The problem (2.8) was considered and studied by Agarwal et al. [1], when  .
.
If  for all
for all  ,
,  and, for all
and, for all  ,
,  is a
is a  -accretive mapping, then (2.7) reduces to the following generalized nonlinear random multivalued operator equation involving
-accretive mapping, then (2.7) reduces to the following generalized nonlinear random multivalued operator equation involving  -accretive mapping in Banach spaces:
-accretive mapping in Banach spaces:
Find  such that
such that  and
and

for all  and
and  .
.
The generalized duality mapping  is defined by
is defined by

for all  , where
, where  is a constant. In particular,
is a constant. In particular,  is the usual normalized duality mapping. It is well known that, in general,
is the usual normalized duality mapping. It is well known that, in general,  for all
for all  and
and  is single-valued if
is single-valued if  is strictly convex (see, e.g., [29]). If
is strictly convex (see, e.g., [29]). If  is a Hilbert space, then
is a Hilbert space, then  becomes the identity mapping of
becomes the identity mapping of  . In what follows we will denote the single-valued generalized duality mapping by
. In what follows we will denote the single-valued generalized duality mapping by  .
.
The modules of smoothness of  is the function
is the function  defined by
defined by

A Banach space  is called uniformly smooth if
is called uniformly smooth if  and
and  is called
is called  -uniformly smooth if there exists a constant
-uniformly smooth if there exists a constant  such that
such that  , where
, where  is a real number.
is a real number.
It is well known that Hilbert spaces,  (or
(or  ) spaces,
) spaces,  and the Sobolev spaces
and the Sobolev spaces  ,
,  , are all
, are all  -uniformly smooth.
-uniformly smooth.
In the study of characteristic inequalities in a  -uniformly smooth Banach space, Xu [30] proved the following result.
-uniformly smooth Banach space, Xu [30] proved the following result.
Lemma 2.8.
Let  be a given real number and
be a given real number and  be a real uniformly smooth Banach space. Then
be a real uniformly smooth Banach space. Then  is
is  -uniformly smooth if and only if there exists a constant
-uniformly smooth if and only if there exists a constant  such that, for all
such that, for all  and
and  , the following inequality holds:
, the following inequality holds:

Definition 2.9.
A random operator  is said to be:
is said to be:
(a) -strongly accretive if there exists
-strongly accretive if there exists  such that
such that

for all  and
and  , where
, where  is a real-valued random variable;
is a real-valued random variable;
(b) -Lipschitz continuous if there exists a real-valued random variable
-Lipschitz continuous if there exists a real-valued random variable  such that
such that

for all  and
and  .
.
Definition 2.10.
Let  be a random operator. A operator
be a random operator. A operator  is said to be:
is said to be:
(a) -strongly accretive with respect to
-strongly accretive with respect to  in the first argument if there exists
in the first argument if there exists  such that
such that

for all  and
and  , where
, where  is a real-valued random variable;
is a real-valued random variable;
(b) -Lipschitz continuous in the first argument if there exists a real-valued random variable
-Lipschitz continuous in the first argument if there exists a real-valued random variable  such that
such that

for all  and
and  .
.
Similarly, we can define the Lipschitz continuity in the second argument and third argument of  .
.
Definition 2.11.
Let  be a random operator
be a random operator  be a random operator and
be a random operator and  be a random multivalued operator. Then
be a random multivalued operator. Then  is said to be:
is said to be:
(a) -accretive if
-accretive if

for all  ,
,  and
and  where
where  , for all
, for all  ;
;
(b)strictly -accretive if
-accretive if

for all  ,
,  ,
,  and
and  and the equality holds if and only if
and the equality holds if and only if  for all
for all  ;
;
(c) -strongly
-strongly -accretive if there exists a real-valued random variable
-accretive if there exists a real-valued random variable  such that, for any
such that, for any  ,
,

for all  ,
,  ,
,  and
and  .
.
Definition 2.12.
Let  be a single-valued mapping,
be a single-valued mapping,  be a single-valued mapping,
be a single-valued mapping,  be a multivalued mapping.
be a multivalued mapping.
(i) is said to be m-accretive if
is said to be m-accretive if  is accretive and
is accretive and  for all
for all  and
and  , where
, where  is identity operator on
is identity operator on  ;
;
(ii) is said to be generalized m-accretive if
is said to be generalized m-accretive if  is
is  -accretive and
-accretive and  for all
for all  and
and  ;
;
(iii) is said to be
is said to be  -accretive if
-accretive if  is accretive and
is accretive and  for all
for all  and
and  ;
;
(iv) is said to be
is said to be  -accretive if
-accretive if  is
is  -accretive and
-accretive and  for all
for all  and
and  .
.
Remark 2.13.
If  is a Hilbert space, then (a)–(c) of Definition 2.11 reduce to the definition of
is a Hilbert space, then (a)–(c) of Definition 2.11 reduce to the definition of  -monotonicity, strict
-monotonicity, strict  -monotonicity and strong
-monotonicity and strong  -monotonicity, respectively, if
-monotonicity, respectively, if  is uniformly smooth and
is uniformly smooth and  , then (a)–(c) of Definition 2.11 reduce to the definitions of accretive, strictly accretive and strongly accretive in uniformly smooth Banach spaces, respectively.
, then (a)–(c) of Definition 2.11 reduce to the definitions of accretive, strictly accretive and strongly accretive in uniformly smooth Banach spaces, respectively.
Definition 2.14.
The operator  is said to be:
is said to be:  -Lipschitz continuous if there exists a real-valued random variable
-Lipschitz continuous if there exists a real-valued random variable  such that
such that

for all  and
and  .
.
Definition 2.15.
A multivalued measurable operator  is said to be
is said to be  -
- -Lipschitz continuous if there exists a measurable function
-Lipschitz continuous if there exists a measurable function  such that, for any
such that, for any  ,
,

for all  .
.
Definition 2.16.
Let  be a
be a  -accretive random operator and
-accretive random operator and  be
be  -strongly monotone random operator. Then the proximal operator
-strongly monotone random operator. Then the proximal operator is defined as follows:
is defined as follows:

for all  and
and  , where
, where  is a measurable function and
is a measurable function and  is a strictly monotone operator.
is a strictly monotone operator.
Lemma 2.17 (see [31]).
Let  be a
be a  -Lipschitz continuous operator,
-Lipschitz continuous operator,  be a r-strongly
be a r-strongly  -accretive operator and
-accretive operator and  be an
be an  -accretive operator. Then, the proximal operator
-accretive operator. Then, the proximal operator  is
is  -Lipschitz continuous, that is,
-Lipschitz continuous, that is,

3. Random Iterative Algorithms
In this section, we suggest and analyze a new class of iterative methods and construct some new random iterative algorithms for solving (2.7).
Lemma 3.1.
The set of measurable mapping  a random solution of problem (2.7) if and only if for all
a random solution of problem (2.7) if and only if for all  , and
, and

Proof.
The proof directly follows from the definition of  as follows:
as follows:

Algorithm 3.2.
Suppose that  be three random fuzzy mappings satisfying the condition (C). Let
be three random fuzzy mappings satisfying the condition (C). Let  be
be  -continuous random multivalued mappings induced by
-continuous random multivalued mappings induced by  ,
,  , and
, and  , respectively. Let
, respectively. Let  ,
,  and
and  be random single-valued operators. Let
be random single-valued operators. Let  be a random multivalued operator such that for each fixed
be a random multivalued operator such that for each fixed  and
and  ,
,  be a
be a  -accretive mapping and
-accretive mapping and 
 . For any given measurable mapping
. For any given measurable mapping  , the multivalued mappings
, the multivalued mappings  are measurable by Lemma 2.5. Then, there exists measurable selections
are measurable by Lemma 2.5. Then, there exists measurable selections  and
and  by Himmelberg [6]. Set
by Himmelberg [6]. Set

where 
 and
and  are the same as in Lemma 3.1. Then it is easy to know that
are the same as in Lemma 3.1. Then it is easy to know that  is measurable. Since
is measurable. Since  ,
, and
and  , by Lemma 2.6, there exist measurable selections
, by Lemma 2.6, there exist measurable selections  and
and  such that for all
such that for all  ,
,

By induction, we can define the sequences  ,
,  ,
,  and
and  inductively satisfying
inductively satisfying

From Algorithm 3.2, we can get the following algorithms.
Algorithm 3.3.
Suppose that  ,
,  ,
,  ,
,  ,
,  and
and  are the same as in Algorithm 3.2. Let
are the same as in Algorithm 3.2. Let  be a random single-valued operator,
be a random single-valued operator,  and
and  for all
for all  and
and  . Then, for given measurable
. Then, for given measurable  , we have
, we have

Algorithm 3.4.
Let  be a random multivalued operator such that for each fixed
be a random multivalued operator such that for each fixed  ,
,  is a
is a  -accretive mapping and
-accretive mapping and  . If
. If  ,
,  ,
,  ,
,  ,
,  and
and  are the same as in Algorithm 3.2, then for given measurable
are the same as in Algorithm 3.2, then for given measurable  , we have
, we have

4. Existence and Convergence Theorems
In this section, we prove the existence and convergence theorems of the generalized random iterative algorithm for this nonlinear random equations with random fuzzy mappings in  -uniformly smooth Banach spaces.
-uniformly smooth Banach spaces.
Theorem 4.1.
Suppose that  is a
is a  -uniformly smooth and separable real Banach space,
-uniformly smooth and separable real Banach space,  is
is  -strongly accretive and
-strongly accretive and  -Lipschitz continuous,
-Lipschitz continuous,  be
be  -Lipschitz continuous,
-Lipschitz continuous,  is r-strongly
is r-strongly  -accretive and
-accretive and  -Lipschitz continuous and
-Lipschitz continuous and  is a random multivalued operator such that for each fixed
is a random multivalued operator such that for each fixed  and
and  ,
,  is a
is a  -accretive mapping and
-accretive mapping and  . Let
. Let  be a
be a  -Lipschitz continuous random operator and
-Lipschitz continuous random operator and  be
be  -Lipschitz continuous in the first argument,
-Lipschitz continuous in the first argument,  -Lipschitz continuous in the second argument and
-Lipschitz continuous in the second argument and  -Lipschitz continuous in the third argument, respectively. Let
-Lipschitz continuous in the third argument, respectively. Let  be three random fuzzy mappings satisfying the condition (C),
be three random fuzzy mappings satisfying the condition (C),  be three random multivalued mappings induced by the mappings
be three random multivalued mappings induced by the mappings  , respectively,
, respectively,  and
and  are
are  -Lipschitz continuous with constants
-Lipschitz continuous with constants  ,
,  and
and  , respectively. If for each real-valued random variables
, respectively. If for each real-valued random variables  and
and  such that, for any
such that, for any  ,
,  ,
,

and the following conditions hold:

where  is the same as in Lemma 2.8 for any
is the same as in Lemma 2.8 for any  . If there exist real-valued random variables
. If there exist real-valued random variables  ,
, then there exist
then there exist  and
and  such that
such that  is solution of (2.7) and
is solution of (2.7) and

as  , where
, where  ,
,  ,
,  and
and  are iterative sequences generated by Algorithm 3.2.
are iterative sequences generated by Algorithm 3.2.
Proof.
From Algorithm 3.2, Lemma 2.17 and (4.1), we compute

By using  is a strongly accretive and Lipschitz continuous, we have
is a strongly accretive and Lipschitz continuous, we have

that is

where  is the same as in Lemma 2.8.
is the same as in Lemma 2.8.
By Lipschitz continuity of  in the first, second and third argument,
in the first, second and third argument,  ,
,  ,
,  is
is  -Lipschitz continuous,
-Lipschitz continuous,  -Lipschitz continuous,
-Lipschitz continuous,  -Lipschitz continuous, respectively, and
-Lipschitz continuous, respectively, and  ,
,  , and
, and  are
are  -Lipschitz continuous, we have
-Lipschitz continuous, we have

Using (4.6)–(4.7) in (4.4), we obtain for all  ,
,

where

Letting

Thus  ,
,  as
as  . From (4.2), we know that
. From (4.2), we know that  , for all
, for all  . Using the same arguments as those used in the proof of (Lan et al. [11, Theorem 3.1, page 14]) it follows that
. Using the same arguments as those used in the proof of (Lan et al. [11, Theorem 3.1, page 14]) it follows that  and
and  are Cauchy sequences. Thus by the completeness of
are Cauchy sequences. Thus by the completeness of  , there exist
, there exist  such that
such that  as
as  .
.
Next, we show that  , we have
, we have

This implies that  . Similarly, we can get
. Similarly, we can get  and
and  for all
for all  . Therefore, from Algorithm 3.2 and the continuity of
. Therefore, from Algorithm 3.2 and the continuity of  ,
,  and
and  , we obtain
, we obtain

By Lemma 3.1, we know that  is a solution of (2.7). This completes the proof.
is a solution of (2.7). This completes the proof.
Remark 4.2.
If the fuzzy mapping  ,
,  and
and  are multivalued operators,
are multivalued operators,  , and multivalued
, and multivalued  is generalized
is generalized  -accretive mapping,
-accretive mapping,  is
is  -strongly monotone,
-strongly monotone,  is
is  -strongly accretive with respect to
-strongly accretive with respect to  , then the result is Theorem 3.1 of Lan et al. [11].
, then the result is Theorem 3.1 of Lan et al. [11].
From Theorem 4.1, we can get the following theorems.
Theorem 4.3.
Let  ,
,  ,
,  ,
,  ,
,  and
and  are the same as in Theorem 4.1. Assume that
are the same as in Theorem 4.1. Assume that  is a random multivalued operator such that, for each fixed
is a random multivalued operator such that, for each fixed  and
and  ,
,  is a
is a  -accretive mapping. Let
-accretive mapping. Let  be
be  -Lipschitz continuous,
-Lipschitz continuous,  be a
be a  -Lipschitz continuous random operator,
-Lipschitz continuous random operator,  be
be  -Lipschitz continuous and
-Lipschitz continuous and  be
be  -Lipschitz continuous in the first argument and
-Lipschitz continuous in the first argument and  -Lipschitz continuous in the second argument, respectively. If there exist real-valued random variables
-Lipschitz continuous in the second argument, respectively. If there exist real-valued random variables  and
and  such that (4.13) holds:
such that (4.13) holds:

for all  , where
, where  is the same as in Lemma 2.8, for any
is the same as in Lemma 2.8, for any  , the iterative sequences
, the iterative sequences  ,
,  and
and  defined by Algorithm 3.3 converge strongly to the solution
defined by Algorithm 3.3 converge strongly to the solution  of (2.8).
of (2.8).
Theorem 4.4.
Suppose that  ,
,  ,
,  ,
,  ,
,  ,
,  and
and  are the same as in Algorithm 3.2 Let
are the same as in Algorithm 3.2 Let  be a random multivalued operator such that, for each fixed
be a random multivalued operator such that, for each fixed  ,
,  is a
is a  -accretive mapping and
-accretive mapping and  . If there exists a real-valued random variable
. If there exists a real-valued random variable  such that, for any
such that, for any  , and the following conditions hold:
, and the following conditions hold:

where  is the same as in Lemma 2.8, for any
is the same as in Lemma 2.8, for any  , the iterative sequences
, the iterative sequences  ,
,  and
and  defined by Algorithm 3.4 converge strongly to the solution
defined by Algorithm 3.4 converge strongly to the solution  of (2.9).
of (2.9).
Remark 4.5.
We note that for suitable choices of the mappings  and space
and space  . Theorems 4.1–4.4 reduces to many known results of generalized variational inclusions as special cases (see [1, 3, 4, 20–25, 32] and the references therein).
. Theorems 4.1–4.4 reduces to many known results of generalized variational inclusions as special cases (see [1, 3, 4, 20–25, 32] and the references therein).
References
Agarwal RP, Cho YJ, Huang N-J: Generalized nonlinear variational inclusions involving maximal
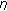 -monotone mappings. In Nonlinear Analysis and Applications: To V. Lakshmikantham on His 80th Birthday. Volume 1, 2. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2003:59–73.
-monotone mappings. In Nonlinear Analysis and Applications: To V. Lakshmikantham on His 80th Birthday. Volume 1, 2. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2003:59–73.Agarwal RP, Khan MF, O'Regan D, Salahuddin : On generalized multivalued nonlinear variational-like inclusions with fuzzy mappings. Advances in Nonlinear Variational Inequalities 2005, 8(1):41–55.
Huang N-J: Generalized nonlinear variational inclusions with noncompact valued mappings. Applied Mathematics Letters 1996, 9(3):25–29. 10.1016/0893-9659(96)00026-2
Huang N-J, Fang Y-P: A new class of general variational inclusions involving maximal
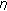 -monotone mappings. Publicationes Mathematicae Debrecen 2003, 62(1–2):83–98.
-monotone mappings. Publicationes Mathematicae Debrecen 2003, 62(1–2):83–98.Huang N-J, Fang YP, Deng CX: Nonlinear variational inclusions involving generalized -accretive mappings. Proceedings of the Bellman Continuum: International Workshop on Uncertain Systems and Soft Computing, July 2002, Beijing, China 323–327.
Himmelberg CJ: Measurable relations. Fundamenta Mathematicae 1975, 87: 53–72.
Huang N-J: Nonlinear implicit quasi-variational inclusions involving generalized
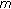 -accretive mappings. Archives of Inequalities and Applications 2004, 2(4):413–425.
-accretive mappings. Archives of Inequalities and Applications 2004, 2(4):413–425.Lan H-Y: Projection iterative approximations for a new class of general random implicit quasi-variational inequalities. Journal of Inequalities and Applications 2006, 2006:-17.
Lan H-Y: Approximation solvability of nonlinear random
 -resolvent operator equations with random relaxed cocoercive operators. Computers & Mathematics with Applications 2009, 57(4):624–632. 10.1016/j.camwa.2008.09.036
-resolvent operator equations with random relaxed cocoercive operators. Computers & Mathematics with Applications 2009, 57(4):624–632. 10.1016/j.camwa.2008.09.036Lan H-Y: A class of nonlinear
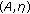 -monotone operator inclusion problems with relaxed cocoercive mappings. Advances in Nonlinear Variational Inequalities 2006, 9(2):1–11.
-monotone operator inclusion problems with relaxed cocoercive mappings. Advances in Nonlinear Variational Inequalities 2006, 9(2):1–11.Lan H-Y, Cho YJ, Xie W: General nonlinear random equations with random multivalued operator in Banach spaces. Journal of Inequalities and Applications 2009, 2009:-17.
Jin M-M, Liu Q-K: Nonlinear quasi-variational inclusions involving generalized
 -accretive mappings. Nonlinear Functional Analysis and Applications 2004, 9(3):485–494.
-accretive mappings. Nonlinear Functional Analysis and Applications 2004, 9(3):485–494.Lan HY, Kim JK, Huang N-J: On the generalized nonlinear quasi-variational inclusions involving non-monotone set-valued mappings. Nonlinear Functional Analysis and Applications 2004, 9(3):451–465.
Lan H-Y, Liu Q-K, Li J: Iterative approximation for a system of nonlinear variational inclusions involving generalized
 -accretive mappings. Nonlinear Analysis Forum 2004, 9(1):33–42.
-accretive mappings. Nonlinear Analysis Forum 2004, 9(1):33–42.Lan H-Y, He Z-Q, Li J: Generalized nonlinear fuzzy quasi-variational-like inclusions involving maximal
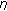 -monotone mappings. Nonlinear Analysis Forum 2003, 8(1):43–54.
-monotone mappings. Nonlinear Analysis Forum 2003, 8(1):43–54.Liu L-W, Li Y-Q: On generalized set-valued variational inclusions. Journal of Mathematical Analysis and Applications 2001, 261(1):231–240. 10.1006/jmaa.2001.7493
Verma RU, Khan MF, Salahuddin : Generalized setvalued nonlinear mixed quasivariational-like inclusions with fuzzy mappings. Advances in Nonlinear Variational Inequalities 2005, 8(2):11–37.
Ahmad R, Bazán FF: An iterative algorithm for random generalized nonlinear mixed variational inclusions for random fuzzy mappings. Applied Mathematics and Computation 2005, 167(2):1400–1411. 10.1016/j.amc.2004.08.025
Chang SS: Fixed Point Theory with Applications. Chongqing, Chongqing, China; 1984.
Chang SS: Variational Inequality and Complementarity Problem Theory with Applications. Shanghai Scientific and Technological Literature, Shanghai, China; 1991.
Chang SS, Huang N-J: Generalized random multivalued quasi-complementarity problems. Indian Journal of Mathematics 1993, 35(3):305–320.
Cho YJ, Shim SH, Huang N-J, Kang SM: Generalized strongly nonlinear implicit quasi-variational inequalities for fuzzy mappings. In Set Valued Mappings with Applications in Nonlinear Analysis, Mathematical Analysis and Applications. Volume 4. Taylor & Francis, London, UK; 2002:63–77.
Cho YJ, Huang N-J, Kang SM: Random generalized set-valued strongly nonlinear implicit quasi-variational inequalities. Journal of Inequalities and Applications 2000, 5(5):515–531. 10.1155/S1025583400000308
Cho YJ, Lan H-Y: Generalized nonlinear random
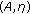 -accretive equations with random relaxed cocoercive mappings in Banach spaces. Computers & Mathematics with Applications 2008, 55(9):2173–2182. 10.1016/j.camwa.2007.09.002
-accretive equations with random relaxed cocoercive mappings in Banach spaces. Computers & Mathematics with Applications 2008, 55(9):2173–2182. 10.1016/j.camwa.2007.09.002Feng HR, Ding XP: A new system of generalized nonlinear quasi-variational-like inclusions with
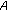 -monotone operators in Banach spaces. Journal of Computational and Applied Mathematics 2009, 225(2):365–373. 10.1016/j.cam.2008.07.048
-monotone operators in Banach spaces. Journal of Computational and Applied Mathematics 2009, 225(2):365–373. 10.1016/j.cam.2008.07.048Huang N-J, Cho YJ: Random completely generalized set-valued implicit quasi-variational inequalities. Positivity 1999, 3(3):201–213. 10.1023/A:1009784323320
Huang N-J, Long X, Cho YJ: Random completely generalized nonlinear variational inclusions with non-compact valued random mappings. Bulletin of the Korean Mathematical Society 1997, 34(4):603–615.
Noor MA, Elsanousi SA: Iterative algorithms for random variational inequalities. Panamerican Mathematical Journal 1993, 3(1):39–50.
Verma RU: A class of projection-contraction methods applied to monotone variational inequalities. Applied Mathematics Letters 2000, 13(8):55–62. 10.1016/S0893-9659(00)00096-3
Xu HK: Inequalities in Banach spaces with applications. Nonlinear Analysis: Theory, Methods & Applications 1991, 16(12):1127–1138. 10.1016/0362-546X(91)90200-K
Ahmad R, Farajzadeh AP: On random variational inclusions with random fuzzy mappings and random relaxed cocoercive mappings. Fuzzy Sets and Systems 2009, 160(21):3166–3174. 10.1016/j.fss.2009.01.002
Huang N-J: Random generalized nonlinear variational inclusions for random fuzzy mappings. Fuzzy Sets and Systems 1999, 105(3):437–444. 10.1016/S0165-0114(97)00222-4
Acknowledgments
This research is supported by the "Centre of Excellence in Mathematics", the Commission on High Education, Thailand. Moreover, N. Onjai-Uea is supported by the "Centre of Excellence in Mathematics", the Commission on High Education, Thailand for Ph.D. Program at King Mongkuts University of Technology Thonburi (KMUTT).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Onjai-Uea, N., Kumam, P. A Generalized Nonlinear Random Equations with Random Fuzzy Mappings in Uniformly Smooth Banach Spaces. J Inequal Appl 2010, 728452 (2010). https://doi.org/10.1155/2010/728452
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/728452
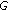 is a single-valued operator,
is a single-valued operator, 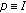 , where
, where  is the identity mapping and
is the identity mapping and 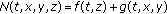 for all
for all 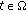 and
and 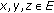 , then (2.7) is equivalent to finding
, then (2.7) is equivalent to finding 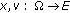 such that
such that 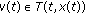 and
and 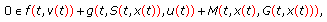
 -monotone mappings. In Nonlinear Analysis and Applications: To V. Lakshmikantham on His 80th Birthday. Volume 1, 2. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2003:59–73.
-monotone mappings. In Nonlinear Analysis and Applications: To V. Lakshmikantham on His 80th Birthday. Volume 1, 2. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2003:59–73.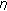 -monotone mappings. Publicationes Mathematicae Debrecen 2003, 62(1–2):83–98.
-monotone mappings. Publicationes Mathematicae Debrecen 2003, 62(1–2):83–98.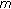 -accretive mappings. Archives of Inequalities and Applications 2004, 2(4):413–425.
-accretive mappings. Archives of Inequalities and Applications 2004, 2(4):413–425. -resolvent operator equations with random relaxed cocoercive operators. Computers & Mathematics with Applications 2009, 57(4):624–632. 10.1016/j.camwa.2008.09.036
-resolvent operator equations with random relaxed cocoercive operators. Computers & Mathematics with Applications 2009, 57(4):624–632. 10.1016/j.camwa.2008.09.036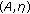 -monotone operator inclusion problems with relaxed cocoercive mappings. Advances in Nonlinear Variational Inequalities 2006, 9(2):1–11.
-monotone operator inclusion problems with relaxed cocoercive mappings. Advances in Nonlinear Variational Inequalities 2006, 9(2):1–11. -accretive mappings. Nonlinear Functional Analysis and Applications 2004, 9(3):485–494.
-accretive mappings. Nonlinear Functional Analysis and Applications 2004, 9(3):485–494. -accretive mappings. Nonlinear Analysis Forum 2004, 9(1):33–42.
-accretive mappings. Nonlinear Analysis Forum 2004, 9(1):33–42.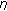 -monotone mappings. Nonlinear Analysis Forum 2003, 8(1):43–54.
-monotone mappings. Nonlinear Analysis Forum 2003, 8(1):43–54. -accretive equations with random relaxed cocoercive mappings in Banach spaces. Computers & Mathematics with Applications 2008, 55(9):2173–2182. 10.1016/j.camwa.2007.09.002
-accretive equations with random relaxed cocoercive mappings in Banach spaces. Computers & Mathematics with Applications 2008, 55(9):2173–2182. 10.1016/j.camwa.2007.09.002 -monotone operators in Banach spaces. Journal of Computational and Applied Mathematics 2009, 225(2):365–373. 10.1016/j.cam.2008.07.048
-monotone operators in Banach spaces. Journal of Computational and Applied Mathematics 2009, 225(2):365–373. 10.1016/j.cam.2008.07.048