- Research Article
- Open access
- Published:
Strong Convergence for Generalized Equilibrium Problems, Fixed Point Problems and Relaxed Cocoercive Variational Inequalities
Journal of Inequalities and Applications volume 2010, Article number: 728028 (2010)
Abstract
We introduce a new iterative scheme for finding the common element of the set of solutions of the generalized equilibrium problems, the set of fixed points of an infinite family of nonexpansive mappings, and the set of solutions of the variational inequality problems for a relaxed  -cocoercive and
-cocoercive and  -Lipschitz continuous mapping in a real Hilbert space. Then, we prove the strong convergence of a common element of the above three sets under some suitable conditions. Our result can be considered as an improvement and refinement of the previously known results.
-Lipschitz continuous mapping in a real Hilbert space. Then, we prove the strong convergence of a common element of the above three sets under some suitable conditions. Our result can be considered as an improvement and refinement of the previously known results.
1. Introduction
Variational inequalities introduced by Stampacchia [1] in the early sixties have had a great impact and influence in the development of almost all branches of pure and applied sciences. It is well known that the variational inequalities are equivalent to the fixed point problems. This alternative equivalent formulation has been used to suggest and analyze in variational inequalities. In particular, the solution of the variational inequalities can be computed using the iterative projection methods. It is well known that the convergence of a projection method requires the operator to be strongly monotone and Lipschitz continuous. Gabay [2] has shown that the convergence of a projection method can be proved for cocoercive operators. Note that cocoercivity is a weaker condition than strong monotonicity.
Equilibrium problem theory provides a novel and unified treatment of a wide class of problems which arise in economics, finance, image reconstruction, ecology, transportation, network, elasticity, and optimization which has been extended and generalized in many directions using novel and innovative technique; see [3, 4]. Related to the equilibrium problems, we also have the problem of finding the fixed points of the nonexpansive mappings. It is natural to construct a unified approach for these problems. In this direction, several authors have introduced some iterative schemes for finding a common element of a set of the solutions of the equilibrium problems and a set of the fixed points of infinitely (finitely) many nonexpansive mappings; see [5–7] and the references therein. In this paper, we suggest and analyze a new iterative method for finding a common element of a set of the solutions of generalized equilibrium problems and a set of fixed points of an infinite family of nonexpansive mappings and the set solution of the variational inequality problems for a relaxed  -cocoercive mapping in a real Hilbert space.
-cocoercive mapping in a real Hilbert space.
Let  be a real Hilbert space and let
be a real Hilbert space and let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  and
and  is the metric projection of
is the metric projection of  onto
onto  Recall that a mapping
Recall that a mapping  is contraction on
is contraction on  if there exists a constant
if there exists a constant  such that
such that  for all
for all  A mapping
A mapping  of
of  into itself is called nonexpansive if
into itself is called nonexpansive if  for all
for all  We denote by
We denote by  the set of fixed points of
the set of fixed points of  , that is,
, that is,  . If
. If  is nonempty, bounded, closed, and convex and
is nonempty, bounded, closed, and convex and  is a nonexpansive mapping of
is a nonexpansive mapping of  into itself, then
into itself, then  is nonempty; see, for example, [8]. We recalled some definitions as follows.
is nonempty; see, for example, [8]. We recalled some definitions as follows.
Definition 1.1.
Let  be a mapping. Then one has the following.
be a mapping. Then one has the following.
(1) is calledmonotone if
is calledmonotone if  for all
for all 
(2) is called
is called  -strongly monotone if there exists a positive real number
-strongly monotone if there exists a positive real number  such that
such that

(3) is called
is called  -Lipschitz continuous if there exists a positive real number
-Lipschitz continuous if there exists a positive real number  such that
such that

(4) is called
is called  -inverse-strongly monotone, [9, 10] if there exists a positive real number
-inverse-strongly monotone, [9, 10] if there exists a positive real number  such that
such that

If  we say that
we say that  is firmly nonexpansive. It is obvious that any
is firmly nonexpansive. It is obvious that any  -inverse-strongly monotone mapping
-inverse-strongly monotone mapping  is monotone and
is monotone and  -Lipschitz continuous.
-Lipschitz continuous.
(5) is calledrelaxed
is calledrelaxed -cocoercive if there exists a positive real number
-cocoercive if there exists a positive real number  such that
such that

For  ,
,  is
is  -strongly monotone. This class of maps is more general than the class of strongly monotone maps. It is easy to see that we have the following implication:
-strongly monotone. This class of maps is more general than the class of strongly monotone maps. It is easy to see that we have the following implication:  -strongly monotonicity
-strongly monotonicity  relaxed
relaxed  -cocoercivity.
-cocoercivity.
(6)A set-valued mapping  is called monotone if for all
is called monotone if for all  ,
,  and
and  imply
imply  . A monotone mapping
. A monotone mapping  is maximal if the graph of
is maximal if the graph of  of
of  is not properly contained in the graph of any other monotone mapping. It is known that a monotone mapping
is not properly contained in the graph of any other monotone mapping. It is known that a monotone mapping  is maximal if and only if for
is maximal if and only if for  ,
,  for every
for every  implies
implies  .
.
Let  be a monotone mapping of
be a monotone mapping of  into
into  and let
and let  be the normal cone to
be the normal cone to  at
at  , that is,
, that is,

Define

Then  is the maximal monotone and
is the maximal monotone and  if and only if
if and only if  ; see [11, 12]
; see [11, 12]
In addition, let  be a inverse-strongly monotone mapping. Let
be a inverse-strongly monotone mapping. Let  be a bifunction of
be a bifunction of  into
into  , where
, where  is the set of real numbers. The generalized equilibrium problem for
is the set of real numbers. The generalized equilibrium problem for  is to find
is to find  such that
such that

The set of such  is denoted by
is denoted by  that is,
that is,

Special Cases
( ) If
) If  (:the zero mapping), then the problem (1.7) is reduced to the equilibrium problem:
(:the zero mapping), then the problem (1.7) is reduced to the equilibrium problem:

The set of solutions of (1.9) is denoted by  that is,
that is,

( ) If
) If  , the problem (1.7) is reduced to the variational inequality problem:
, the problem (1.7) is reduced to the variational inequality problem:

The set of solutions of (1.11) is denoted by  , that is,
, that is,

The generalized equilibrium problem (1.7) is very general in the sense that it includes, as special case, some optimization, variational inequalities, minimax problems, the Nash equilibrium problem in noncooperative games, economics, and others (see, e.g., [4, 13]). Some methods have been proposed to solve the equilibrium problem and the generalized equilibrium problem; see, for instance, [5, 14–28]. Recently, Combettes and Hirstoaga [29] introduced an iterative scheme of finding the best approximation to the initial data when  is nonempty and proved a strong convergence theorem. Very recently, Moudafi [24] introduced an itertive method for finding an element of
is nonempty and proved a strong convergence theorem. Very recently, Moudafi [24] introduced an itertive method for finding an element of  , where
, where  is an inverse-strongly monotone mapping and then proved a weak convergence theorem.
is an inverse-strongly monotone mapping and then proved a weak convergence theorem.
For finding a common element of the set of fixed points of a nonexpansive mapping and the set of solutions of variational inequality problem for an  -inverse-strongly monotone, Takahashi and Toyoda [30] introduced the following iterative scheme:
-inverse-strongly monotone, Takahashi and Toyoda [30] introduced the following iterative scheme:

where  is an
is an  -inverse-strongly monotone mapping,
-inverse-strongly monotone mapping,  is a sequence in (0, 1), and
is a sequence in (0, 1), and  is a sequence in
is a sequence in  . They showed that if
. They showed that if  is nonempty, then the sequence
is nonempty, then the sequence  generated by (1.13) converges weakly to some
generated by (1.13) converges weakly to some  . On the other hand, Shang et al. [31] introduced a new iterative process for finding a common element of the set of fixed points of a nonexpansive mapping and the set of solutions of the variational inequality problem for a relaxed
. On the other hand, Shang et al. [31] introduced a new iterative process for finding a common element of the set of fixed points of a nonexpansive mapping and the set of solutions of the variational inequality problem for a relaxed  -cocoercive mapping in a real Hilbert space. Let
-cocoercive mapping in a real Hilbert space. Let  be a nonexpansive mapping. Starting with arbitrary initial
be a nonexpansive mapping. Starting with arbitrary initial  defined sequences
defined sequences  recursively by
recursively by

They proved that under certain appropriate conditions imposed on  ,
,  ,
,  and
and  , the sequence
, the sequence  converges strongly to
converges strongly to  , where
, where 
In 2008, S. Takahashi and W. Takahashi [27] introduced the following iterative scheme for finding an element of  under some mild conditions. Let
under some mild conditions. Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  . Let
. Let  be an
be an  -inverse-strongly monotone mapping of
-inverse-strongly monotone mapping of  into
into  and let
and let  be a nonexpansive mapping of
be a nonexpansive mapping of  into itself such that
into itself such that  Suppose
Suppose  and let
and let  ,
,  , and
, and  by sequences generated by
by sequences generated by

where  ,
,  and
and  satisfy some parameters controlling conditions. They proved that the sequence
satisfy some parameters controlling conditions. They proved that the sequence  defined by (1.15) converges strongly to a common element of
defined by (1.15) converges strongly to a common element of  .
.
On the other hand, iterative methods for nonexpansive mappings have recently been applied to solve convex minimization problems; see, for example, [32–35] and the references therein. Convex minimization problems have a great impact and influence in the development of almost all branches of pure and applied sciences.
A typical problem is to minimize a quadratic function over the set of the fixed points a nonexpansive mapping in a real Hilbert space  :
:

where  is the fixed point set of a nonexpansive mapping
is the fixed point set of a nonexpansive mapping  on
on  and
and  is a given point in
is a given point in  . Assume that
. Assume that  is a strongly positive bounded linear operator on
is a strongly positive bounded linear operator on  ; that is, there exists a constant
; that is, there exists a constant  such that
such that

In 2006, Marino and Xu [36] considered the following iterative method:

They proved that if the sequence  of parameters satisfies appropriate conditions, then the sequence
of parameters satisfies appropriate conditions, then the sequence  generated by (1.18) converges strongly to the unique of the variational inequality
generated by (1.18) converges strongly to the unique of the variational inequality

which is the optimality condition for the minimization problem

where  is a potential function for
is a potential function for  (i.e.,
(i.e.,  for
for  ).
).
In 2008, Qin et al. [26] proposed the following iterative algorithm:

where  is a strongly positive linear bounded operator and
is a strongly positive linear bounded operator and  is a relaxed cocoercive mapping of
is a relaxed cocoercive mapping of  into
into  . They prove that if the sequences
. They prove that if the sequences  ,
,  and
and  of parameters satisfy appropriate condition, then the sequences
of parameters satisfy appropriate condition, then the sequences  and
and  both converge to the unique solution
both converge to the unique solution  of the variational inequality
of the variational inequality

which is the optimality condition for the minimization problem

where  is a potential function for
is a potential function for  (i.e.,
(i.e.,  for
for  ).
).
Furthermore, for finding approximate common fixed points of an infinite family of nonexpansive mappings  under very mild conditions on the parameters, we need the following definition.
under very mild conditions on the parameters, we need the following definition.
Definition 1.2 (see [37]).
Let  be a sequence of nonexpansive mappings of
be a sequence of nonexpansive mappings of  into itself and let
into itself and let  be a sequence of nonnegative numbers in
be a sequence of nonnegative numbers in  . For each
. For each  , define a mapping
, define a mapping  of
of  into itself as follows:
into itself as follows:

Such a mappings  is called the
is called the  -mapping generated by
-mapping generated by  and
and  . It is obvious that
. It is obvious that  is nonexpansive, and if
is nonexpansive, and if  then
then  .
.
On the other hand, Yao et al. [38] introduced and considered an iterative scheme for finding a common element of the set of solutions of the equilibrium problem and the set of common fixed points of an infinite family of nonexpansive mappings on  . Starting with an arbitrary initial
. Starting with an arbitrary initial  , define sequences
, define sequences  and
and  recursively by
recursively by

where  is a sequence in
is a sequence in  . It is proved [38] that under certain appropriate conditions imposed on
. It is proved [38] that under certain appropriate conditions imposed on  and
and  , the sequence
, the sequence  generated by (1.25) converges strongly to
generated by (1.25) converges strongly to  . Very recently, Qin et al. [6] introduced an iterative scheme for finding a common fixed points of a finite family of nonexpansive mappings, the set of solutions of the variational inequality problem for a relaxed cocoercive mapping, and the set of solutions of the equilibrium problems in a real Hilbert space. Starting with an arbitrary initial
. Very recently, Qin et al. [6] introduced an iterative scheme for finding a common fixed points of a finite family of nonexpansive mappings, the set of solutions of the variational inequality problem for a relaxed cocoercive mapping, and the set of solutions of the equilibrium problems in a real Hilbert space. Starting with an arbitrary initial  , define sequences
, define sequences  and
and  recursively by
recursively by

where  is a relaxed
is a relaxed  -cocoercive mapping and
-cocoercive mapping and  is a strongly positive linear bounded operator. They proved that under certain appropriate conditions imposed on
is a strongly positive linear bounded operator. They proved that under certain appropriate conditions imposed on  and
and  , the sequences
, the sequences  and
and  generated by (1.26) converge strongly to some point
generated by (1.26) converge strongly to some point  , which is a unique solution of the variation inequality:
, which is a unique solution of the variation inequality:

and is also the optimality for some minimization problems.
In this paper, motivated by iterative schemes considered in (1.15), (1.25), and (1.26) we will introduce a new iterative process (3.4) below for finding a common element of the set of fixed points of an infinite family of nonexpansive mappings, the set of solutions of the generalized equilibrium problem, and the set of solutions of variational inequality problem for a relaxed  -cocoercive mapping in a real Hilbert space. The results obtained in this paper improve and extend the recent ones announced by Yao et al. [38], S. Takahashi and W. Takahashi [27], and Qin et al. [6] and many others.
-cocoercive mapping in a real Hilbert space. The results obtained in this paper improve and extend the recent ones announced by Yao et al. [38], S. Takahashi and W. Takahashi [27], and Qin et al. [6] and many others.
2. Preliminaries
Let  be a real Hilbert space with inner product
be a real Hilbert space with inner product  and norm
and norm  . Let
. Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  We denote weak convergence and strong convergence by notations
We denote weak convergence and strong convergence by notations  and
and  , respectively. Recall that the (nearest point) projection
, respectively. Recall that the (nearest point) projection  from
from  to
to  assigns each
assigns each  the unique point in
the unique point in  satisfying the property
satisfying the property

The following characterizes the projection  .
.
We need some facts tools in a real Hilbert space  which are listed as follows.
which are listed as follows.
Lemma 2.1.
For any  ,
, 

It is well known that  is a firmly nonexpansive mapping of
is a firmly nonexpansive mapping of  onto
onto  and satisfies
and satisfies

Moreover,  is characterized by the following properties:
is characterized by the following properties:  and for all
and for all 

Lemma 2.2 (see [39]).
Let  be a Hilbert space, let
be a Hilbert space, let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  and let
and let  be a mapping of
be a mapping of  into
into  . Let
. Let  . Then for
. Then for  ,
,

where  is the metric projection of
is the metric projection of  onto
onto  .
.
It is clear from Lemma 2.2 that variational inequality and fixed point problem are equivalent. This alternative equivalent formulation has played a significant role in the studies of the variational inequalities and related optimization problems.
Lemma 2.3 (see [40]).
Each Hilbert space  satisfies Opials condition; that is, for any sequence
satisfies Opials condition; that is, for any sequence  with
with  , the inequality
, the inequality

holds for each  with
with  .
.
Lemma 2.4 (see [36]).
Assume that  is a strongly positive linear bounded operator on
is a strongly positive linear bounded operator on  with coefficient
with coefficient  and
and  . Then
. Then  .
.
For solving the equilibrium problem for a bifunction  , let us assume that
, let us assume that  satisfies the following conditions:
satisfies the following conditions:
 , for all
, for all 
 is monotone, that is,
is monotone, that is,  , for all
, for all 
 , for all
, for all 
for each  is convex and lower semicontinuous.
is convex and lower semicontinuous.
The following lemma appears implicitly in [4].
Lemma 2.5 (see [4]).
Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  and let
and let  be a bifunction of
be a bifunction of  into
into  satisfying (A1)–(A4). Let
satisfying (A1)–(A4). Let  and
and  . Then, there exists
. Then, there exists  such that
such that

The following lemma was also given in [5].
Lemma 2.6 (see [5]).
Assume that  satisfies (A1)–(A4). For
satisfies (A1)–(A4). For  and
and  , define a mapping
, define a mapping  as follows:
as follows:

for all  . Then, the following holds:
. Then, the following holds:
(1) is single-valued;
is single-valued;
(2) is firmly nonexpansive, that is, for any
is firmly nonexpansive, that is, for any 

(3)
(4) is closed and convex.
is closed and convex.
Remark 2.7.
Replacing  with
with  in (2.7), then there exists
in (2.7), then there exists  , such that
, such that

Lemma 2.8 (see [41]).
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  . Let
. Let  be nonexpansive mappings of
be nonexpansive mappings of  into itself such that
into itself such that  is nonempty, and let
is nonempty, and let  be real numbers such that
be real numbers such that  for every
for every  . Then, for every
. Then, for every  and
and  , the limit
, the limit  exists.
exists.
Using Lemma 2.8, one can define a mapping  of
of  into itself as follows:
into itself as follows:

for every  . Such a
. Such a  is called the
is called the  -mapping generated by
-mapping generated by  and
and  . Throughout this paper, we will assume that
. Throughout this paper, we will assume that  for every
for every  . Then, we have the following results.
. Then, we have the following results.
Lemma 2.9 (see [41]).
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  . Let
. Let  be nonexpansive mappings of
be nonexpansive mappings of  into itself such that
into itself such that  is nonempty, let
is nonempty, let  be real numbers such that
be real numbers such that  for every
for every  . Then,
. Then,  .
.
Lemma 2.10 (see [7]).
If  is a bounded sequence in
is a bounded sequence in  , then
, then  .
.
Lemma 2.11 (see [42]).
Let  and
and  be bounded sequences in a Banach space
be bounded sequences in a Banach space  and let
and let  be a sequence in
be a sequence in  with
with  Suppose
Suppose  for all integers
for all integers  and
and  Then,
Then, 
Lemma 2.12.
Let  be a real Hilbert space. Then the following inequality holds:
be a real Hilbert space. Then the following inequality holds:
(1) ,
,
(2)
for all  .
.
Lemma 2.13 (see [43]).
Assume that  is a sequence of nonnegative real numbers such that
is a sequence of nonnegative real numbers such that

where  is a sequence in
is a sequence in  and
and  is a sequence in
is a sequence in  such that
such that
(1) ,
,
(2) or
or 
Then 
3. Main Results
In this section, we prove a strong convergence theorem of a new iterative method (3.4) for an infinite family of nonexpansive mappings and relaxed  -cocoercive mappings in a real Hilbert space.
-cocoercive mappings in a real Hilbert space.
We first prove the following lemmas.
Lemma 3.1.
Let  be a real Hilbert space, let
be a real Hilbert space, let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  , and let
, and let  be
be  -inverse-strongly monotone. It
-inverse-strongly monotone. It  , then
, then  is a nonexpansive mapping in
is a nonexpansive mapping in  .
.
Proof.
For all  and
and  , we have
, we have

So,  is a nonexpansive mapping of
is a nonexpansive mapping of  into
into  .
.
Lemma 3.2.
Let  be a real Hilbert space, let
be a real Hilbert space, let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  and let
and let  be a relaxed
be a relaxed  -cocoercive and
-cocoercive and  -Lipschitz continuous. If
-Lipschitz continuous. If  ,
,  , then
, then  is a nonexpansive mapping in
is a nonexpansive mapping in  .
.
Proof.
For any  and
and  ,
,  .
.
Putting  , we obtain
, we obtain

that is,  . It follows that
. It follows that

for all  . Thus
. Thus  .
.
So,  is a nonexpansive mapping of
is a nonexpansive mapping of  into
into  .
.
Now, we prove the following main theorem.
Theorem 3.3.
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  , and let
, and let  be a bifunction satisfying (A1)–(A4). Let
be a bifunction satisfying (A1)–(A4). Let
(1) be an infinite family of nonexpansive mappings of
be an infinite family of nonexpansive mappings of  into
into  ;
;
(2) be an
be an  -inverse strongly monotone mappings of
-inverse strongly monotone mappings of  into
into  ;
;
(3) be relaxed
be relaxed  -cocoercive and
-cocoercive and  -Lipschitz continuous mappings of
-Lipschitz continuous mappings of  into
into  .
.
Assume that  . Let
. Let  be a contraction mapping with
be a contraction mapping with  and let
and let  be a strongly positive linear bounded operator on
be a strongly positive linear bounded operator on  with coefficient
with coefficient  and
and  . Let
. Let  ,
,  ,
,  and
and  be sequences generated by
be sequences generated by

where  is the sequence generated by (1.24) and
is the sequence generated by (1.24) and  ,
,  ,
,  and
and  are sequences in
are sequences in  satisfy the following conditions:
satisfy the following conditions:



 and
and 
 ,
,
 ,
, ,
,
 for some
for some  with
with  ,
,  ,
,
 for some
for some  with
with  .
.
Then,  and
and  converge strongly to a point
converge strongly to a point  , where
, where  , which solves the variational inequality
, which solves the variational inequality

which is the optimality condition fot the minimization problem

where  is a potential function for
is a potential function for  (i.e.,
(i.e.,  for
for  ).
).
Proof.
Since  by the condition (C1) and
by the condition (C1) and  , we may assume, without loss of generality, that
, we may assume, without loss of generality, that  . Since
. Since  is a strongly positive bounded linear operator on
is a strongly positive bounded linear operator on  , then
, then

Observe that

that is to say  is positive. It follows that
is positive. It follows that

We will divide the proof of Theorem 3.3 into six steps.
Step 1.
We prove that there exists  such that
such that  .
.
Let  . Note that
. Note that  is a contraction mapping of
is a contraction mapping of  into itself with coefficient
into itself with coefficient  . Then, we have
. Then, we have

Therefore,  is a contraction mapping of
is a contraction mapping of  into itself. Therefore by the Banach Contraction Mapping Principle guarantee that
into itself. Therefore by the Banach Contraction Mapping Principle guarantee that  has a unique fixed point, say
has a unique fixed point, say  . That is,
. That is,  .
.
Step 2.
We prove that  is bounded.
is bounded.
Since

we obtain

From Lemma 2.6, we have  for all
for all  .
.
For any  , it follows from
, it follows from  that
that

So, we have

By Lemma 2.6 again, we have  for all
for all  . If follows that
. If follows that

If we applied Lemma 3.2, we get  and
and  are nonexpansive. Since
are nonexpansive. Since  and
and  is a nonexpansive, we have
is a nonexpansive, we have  , and we have
, and we have

It follows that

which yields that

This in turn implies that

Therefore,  is bounded. We also obtain that
is bounded. We also obtain that  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  and
and  are all bounded.
are all bounded.
Step 3.
We claim that  and
and  .
.
From Lemma 2.6, we have  and
and  . Let
. Let  , we get
, we get  ,
,  , and so
, and so


Putting  in (3.20) and
in (3.20) and  in (3.21), we have
in (3.21), we have

So, from the monotonicity of  , we get
, we get

and hence

Without loss of generality, let us assume that there exists a real number  such that
such that  for all
for all  Then, we have
Then, we have

and hence

where  .
.
Put  ,
,  and
and  . Since
. Since  ,
,  and
and  are nonexpansive, then we have the following some estimates:
are nonexpansive, then we have the following some estimates:

Similarly, we can prove that


Since  and
and  are nonexpansive, we deduce that, for each
are nonexpansive, we deduce that, for each  ,
,

where  is a constant such that
is a constant such that  for all
for all 
Similarly, we can obtain that there exist nonnegative numbers  ,
,  such that
such that

and so are

Observing that

we obtain

which yields that

Substitution of (3.27) and (3.30) into (3.35) yields that

where  is an appropriate constant such that
is an appropriate constant such that  .
.
Observing that

we obtain

which yields that

Substitution of (3.28) and (3.32) into (3.39) yields that

where  is an appropriate constant such that
is an appropriate constant such that  .
.
Substituting (3.26) and (3.36) into (3.40), we obtain

where  is an appropriate constant such that
is an appropriate constant such that  .
.
Substituting (3.41) into (3.29), we obtain

where  is an appropriate constant such that
is an appropriate constant such that  .
.
Define

Observe that from the definition  , we obtain
, we obtain

It follows from (3.32), (3.42), and (3.44) that

where  is an appropriate constant such that
is an appropriate constant such that  .
.
It follows from conditions (C1), (C2), (C3), (C4), (C5), and  for all
for all 

Hence, by Lemma 2.11, we obtain

It follows that

Applying (3.48) and conditions in Theorem 3.3 to (3.26), (3.41), and (3.42), we obtain that

From (3.49), (C2), (C5), and  for all
for all  , we also have
, we also have

Since  , we have
, we have

that is,

By (C1), (C3), and (3.48) it follows that

Step 4.
We claim that the following statements hold:
(i) ;
;
(ii) ;
;
(iii) .
.
Since  is relaxed
is relaxed  -cocoercive and
-cocoercive and  -Lipschitz continuous mappings, by the assumptions imposed on
-Lipschitz continuous mappings, by the assumptions imposed on  for any
for any  , we have
, we have

Similarly, we have

Observe that

where

It follows from condition (C1) that

Substituting (3.54) into (3.56), and using condition (C6), we have

It follows that

Since  as
as  and (3.48), we obtain
and (3.48), we obtain

Note that


Using (3.56) again, we have

Substituting (3.62) into (3.64) and using condition (C2) and (C6), we have

It follows that

Since  as
as  and (3.48), we obtain
and (3.48), we obtain

In a similar way, we can prove

By (2.3), we also have

which yields that

Substituting (3.70) into (3.56), we have

It follows that

Applying  ,
,  and
and  as
as  to the last inequality, we have
to the last inequality, we have

On the other hand, we have

which yields that

Similarly, we can prove


Substituting (3.75) into (3.56), we have

which yields that

Applying (3.48) and (3.61) to the last inequality, we have

Using (3.64) again, we have

which implies that

From (3.48) and (3.67), we obtain

By using the same argument, we can prove that

Note that

Since  and
and  as
as  , respectively, we also have
, respectively, we also have

On the other hand, we observe

Applying (3.73), (3.83), (3.84), and (3.86), we have

On the other hand, we have

Substituting (3.89) into (3.64) and using conditions (C2) and (C7), we have

This implies that

In view of the restrictions (C2) and (C7), we obtain that

Let  . Since
. Since  and
and  is firmly nonexpansive (Lemma 2.6), then we obtain
is firmly nonexpansive (Lemma 2.6), then we obtain

So, we obtain

Therefore, we have

It follows that

Using  ,
,  as
as  , (3.48), (3.88), and (3.92), we obtain
, (3.48), (3.88), and (3.92), we obtain

Since  , we obtain
, we obtain

Note that

and thus from (3.88) and (3.97), we have

Observe that

Applying (3.53) and (3.100), we obtain

Let  be the mapping defined by (2.11). Since
be the mapping defined by (2.11). Since  is bounded, applying Lemma 2.10 and (3.102), we have
is bounded, applying Lemma 2.10 and (3.102), we have

Step 5.
We claim that  where
where  is the unique solution of the variational inequality
is the unique solution of the variational inequality  for all
for all 
Since  is a unique solution of the variational inequality (3.5), to show this inequality, we choose a subsequence
is a unique solution of the variational inequality (3.5), to show this inequality, we choose a subsequence  of
of  such that
such that

Since  is bounded, there exists a subsequence
is bounded, there exists a subsequence  of
of  which converges weakly to
which converges weakly to  . Without loss of generality, we can assume that
. Without loss of generality, we can assume that  From
From  we obtain
we obtain  . Next, We show that
. Next, We show that  , where
, where  .
.
-
(a)
First, we prove
 .
.
Since  , we know that
, we know that

From (A2), we also have

Replacing  by
by  , we have
, we have

For any  with
with  and
and  let
let  Since
Since  and
and  we have
we have  So, from (3.107) we have
So, from (3.107) we have

Since  is Lipschitz continuous, from (3.97), we have
is Lipschitz continuous, from (3.97), we have  as
as  .
.
Further, from the monotonicity of  , we get that
, we get that

It follows from (A4) and (3.108) that

From (A1), (A4), and (3.110), we also have

and hence

Letting  in the above inequality, we have, for each
in the above inequality, we have, for each  ,
,

Thus 
-
(b)
Next, we show that
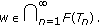
By Lemma 2.9, we have  . Assume
. Assume  Since
Since  we know that
we know that  and
and  and it follows by the Opial's condition (Lemma 2.3) that
and it follows by the Opial's condition (Lemma 2.3) that

that is a contradiction. Thus, we have  .
.
-
(c)
Finally, Now we prove that
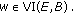 Define,
Define, 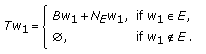 (3.115)
(3.115)
Since  is relaxed
is relaxed  -cocoercive and condition (C6), we have
-cocoercive and condition (C6), we have

which yields that  is monotone. Then,
is monotone. Then,  is maximal monotone. Let
is maximal monotone. Let  Since
Since  and
and  we have
we have  On the other hand, from
On the other hand, from  we have
we have

and hence

Therefore, we have

which implies that

Since  is maximal monotone, we have
is maximal monotone, we have  and hence
and hence  That is,
That is,  , where
, where  . Since
. Since  , it follows that
, it follows that

On the other hand, we have

From (3.53) and (3.121), we obtain that

Step 6.
Finally, we show that  and
and  converge strongly to
converge strongly to  .
.
Indeed, from (3.4) and Lemma 2.4, we obtain

Since  ,
,  and
and  are bounded, we can take a constant
are bounded, we can take a constant  such that
such that

for all  . It then follows that
. It then follows that

where

Using (C1), (3.121), and (3.123), we get  ,
,  and
and  . Applying Lemma 2.13 to (3.126), we conclude that
. Applying Lemma 2.13 to (3.126), we conclude that  in norm. Finally, noticing
in norm. Finally, noticing  we also conclude that
we also conclude that  in norm. This completes the proof.
in norm. This completes the proof.
Corollary 3.4.
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  . Let
. Let  be a bifunction satisfying (A1)–(A4), let
be a bifunction satisfying (A1)–(A4), let  be relaxed
be relaxed  -cocoercive and
-cocoercive and  -Lipschitz continuous mappings, and let
-Lipschitz continuous mappings, and let  be an infinite family of nonexpansive mappings of
be an infinite family of nonexpansive mappings of  into itself such that
into itself such that  . Let
. Let  be a contraction mapping of
be a contraction mapping of  into itself with
into itself with  . Let
. Let  ,
, ,
, and
and  be sequences generated by
be sequences generated by

where  is the sequence generated by (1.24) and
is the sequence generated by (1.24) and  ,
,  ,
,  , and
, and  are sequences in
are sequences in  and
and  is a real sequence in
is a real sequence in  satisfying the following conditions:
satisfying the following conditions:
 ,
,




 ,
,  ,
, 
 for some
for some  with
with  ,
,  .
.
Then,  and
and  converge strongly to a point
converge strongly to a point  , where
, where  .
.
Proof.
Put  ,
,  ,
,  (:the zero mapping) and
(:the zero mapping) and  in Theorem 3.3. Then
in Theorem 3.3. Then  and for any
and for any  , we see that
, we see that

Let  be a sequence satisfying the restriction:
be a sequence satisfying the restriction:  , where
, where  . Then we can obtain the desired conclusion easily from Theorem 3.3.
. Then we can obtain the desired conclusion easily from Theorem 3.3.
Corollary 3.5.
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  . Let
. Let  be an infinite family of nonexpansive mappings of
be an infinite family of nonexpansive mappings of  into itself and let
into itself and let  be relaxed
be relaxed  -cocoercive and
-cocoercive and  -Lipschitz continuous mappings such that
-Lipschitz continuous mappings such that  . Let
. Let  be a contraction mapping with
be a contraction mapping with  and let
and let  be a strongly positive linear bounded operator on
be a strongly positive linear bounded operator on  with coefficient
with coefficient  and
and  . Let
. Let  ,
, and
and  be sequences generated by
be sequences generated by

where  is the sequence generated by (1.24) and
is the sequence generated by (1.24) and  ,
,  ,
,  and
and  are sequences in
are sequences in  satisfying the following conditions:
satisfying the following conditions:



 ,
,
 ,
,  ,
, 
 for some
for some  with
with  ,
,  .
.
Then,  converges strongly to a point
converges strongly to a point  , where
, where  , which solves the variational inequality
, which solves the variational inequality

which is the optimality condition fot the minimization problem

where  is a potential function for
is a potential function for  (i.e.,
(i.e.,  for
for  ).
).
Proof.
Put  ,
,  for all
for all  and
and  for all
for all  in Theorem 3.3. Then, we have
in Theorem 3.3. Then, we have  . So, by Theorem 3.3, we can conclude the desired conclusion easily.
. So, by Theorem 3.3, we can conclude the desired conclusion easily.
References
Stampacchia G: Formes bilinéaires coercitives sur les ensembles convexes. Comptes Rendus Academy of Sciences 1964, 258: 4413–4416.
Gabay D: Applications of the method of multipliers to variational inequalities. In Augmented Lagrangian Methods. Edited by: Fortin M, Glowinski R. North-Holland, Amsterdam, The Netherlands; 1983:299–331.
Noor MA, Oettli W: On general nonlinear complementarity problems and quasi-equilibria. Le Matematiche 1994, 49(2):313–331.
Blum E, Oettli W: From optimization and variational inequalities to equilibrium problems. The Mathematics Student 1994, 63(1–4):123–145.
Flåm SD, Antipin AS: Equilibrium programming using proximal-like algorithms. Mathematical Programming 1997, 78(1):29–41.
Qin X, Shang M, Su Y: Strong convergence of a general iterative algorithm for equilibrium problems and variational inequality problems. Mathematical and Computer Modelling 2008, 48(7–8):1033–1046. 10.1016/j.mcm.2007.12.008
Yao Y, Liou Y-C, Yao J-C: Convergence theorem for equilibrium problems and fixed point problems of infinite family of nonexpansive mappings. Fixed Point Theory and Applications 2007, 2007:-12.
Takahashi W: Nonlinear Functional Analysis, Fixed Point Theory and Its Applications. Yokohama, Yokohama, Japan; 2000:iv+276.
Verma RU: Generalized system for relaxed cocoercive variational inequalities and projection methods. Journal of Optimization Theory and Applications 2004, 121(1):203–210.
Verma RU: General convergence analysis for two-step projection methods and applications to variational problems. Applied Mathematics Letters 2005, 18(11):1286–1292. 10.1016/j.aml.2005.02.026
Rockafellar RT: On the maximality of sums of nonlinear monotone operators. Transactions of the American Mathematical Society 1970, 149: 75–88. 10.1090/S0002-9947-1970-0282272-5
Iiduka H, Takahashi W: Strong convergence theorems for nonexpansive mappings and inverse-strongly monotone mappings. Nonlinear Analysis: Theory, Methods & Applications 2005, 61(3):341–350. 10.1016/j.na.2003.07.023
Moudafi A, Théra M: Proximal and dynamical approaches to equilibrium problems. In Ill-Posed Variational Problems and Regularization Techniques (Trier, 1998), Lecture Notes in Economics and Mathematical Systems. Volume 477. Springer, Berlin, Germany; 1999:187–201.
Qin X, Cho YJ, Kang SM: Viscosity approximation methods for generalized equilibrium problems and fixed point problems with applications. Nonlinear Analysis: Theory, Methods & Applications 2010, 72(1):99–112. 10.1016/j.na.2009.06.042
Cho YJ, Qin X, Kang SM: Some results for equilibrium problems and fixed point problems in Hilbert spaces. Journal of Computational Analysis and Applications 2009, 11(2):294–316.
Cho YJ, Qin X, Kang JI: Convergence theorems based on hybrid methods for generalized equilibrium problems and fixed point problems. Nonlinear Analysis: Theory, Methods & Applications 2009, 71(9):4203–4214. 10.1016/j.na.2009.02.106
Hu CS, Cai G: Viscosity approximation schemes for fixed point problems and equilibrium problems and variational inequality problems. Nonlinear Analysis: Theory, Methods & Applications 2010, 72(3–4):1792–1808. 10.1016/j.na.2009.09.021
Huang N-J, Lan H-Y, Teo KL: On the existence and convergence of approximate solutions for equilibrium problems in Banach spaces. Journal of Inequalities and Applications 2007, 2007:-14.
Jaiboon C, Kumam P: Strong convergence theorems for solving equilibrium problems and fixed point problems of -strict pseudo-contraction mappings by two hybrid projection methods. Journal of Computational and Applied Mathematics. In press
Jaiboon C, Kumam P: A hybrid extragradient viscosity approximation method for solving equilibrium problems and fixed point problems of infinitely many nonexpansive mappings. Fixed Point Theory and Applications 2009, 2009:-32.
Jaiboon C, Chantarangsi W, Kumam P: A convergence theorem based on a hybrid relaxed extragradient method for generalized equilibrium problems and fixed point problems of a finite family of nonexpansive mappings. Nonlinear Analysis: Hybrid Systems 2010, 4(1):199–215. 10.1016/j.nahs.2009.09.009
Kangtunyakarn A, Suantai S: A new mapping for finding common solutions of equilibrium problems and fixed point problems of finite family of nonexpansive mappings. Nonlinear Analysis: Theory, Methods & Applications 2009, 71(10):4448–4460. 10.1016/j.na.2009.03.003
Liu Q-Y, Zeng W-Y, Huang N-J: An iterative method for generalized equilibrium problems, fixed point problems and variational inequality problems. Fixed Point Theory and Applications 2009, 2009:-20.
Moudafi A: Weak convergence theorems for nonexpansive mappings and equilibrium problems. Journal of Nonlinear and Convex Analysis 2008, 9(1):37–43.
Peng J-W, Wang Y, Shyu DS, Yao J-C: Common solutions of an iterative scheme for variational inclusions, equilibrium problems, and fixed point problems. Journal of Inequalities and Applications 2008, 2008:-15.
Qin X, Shang M, Su Y: A general iterative method for equilibrium problems and fixed point problems in Hilbert spaces. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(11):3897–3909. 10.1016/j.na.2007.10.025
Takahashi S, Takahashi W: Strong convergence theorem for a generalized equilibrium problem and a nonexpansive mapping in a Hilbert space. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(3):1025–1033. 10.1016/j.na.2008.02.042
Zeng W-Y, Huang N-J, Zhao C-W: Viscosity approximation methods for generalized mixed equilibrium problems and fixed points of a sequence of nonexpansive mappings. Fixed Point Theory and Applications 2008, 2008:-15.
Combettes PL, Hirstoaga SA: Equilibrium programming in Hilbert spaces. Journal of Nonlinear and Convex Analysis 2005, 6: 117–136.
Takahashi W, Toyoda M: Weak convergence theorems for nonexpansive mappings and monotone mappings. Journal of Optimization Theory and Applications 2003, 118(2):417–428. 10.1023/A:1025407607560
Shang M, Su Y, Qin X: Strong convergence theorem for nonexpansive mappings and relaxed cocoercive mappings. International Journal of Applied Mathematics and Mechanics 2007, 3(4):24–34.
Deutsch F, Yamada I: Minimizing certain convex functions over the intersection of the fixed point sets of nonexpansive mappings. Numerical Functional Analysis and Optimization 1998, 19(1–2):33–56.
Yamada I: The hybrid steepest descent method for the variational inequality problem over the intersection of fixed point sets of nonexpansive mappings. In Inherently Parallel Algorithms in Feasibility and Optimization and Their Applications (Haifa, 2000), Studies in Computational Mathematics. Volume 8. Edited by: Butnariu D, Censor Y, Reich S. North-Holland, Amsterdam, The Netherlands; 2001:473–504.
Xu H-K: Iterative algorithms for nonlinear operators. Journal of the London Mathematical Society 2002, 66(1):240–256. 10.1112/S0024610702003332
Xu HK: An iterative approach to quadratic optimization. Journal of Optimization Theory and Applications 2003, 116(3):659–678. 10.1023/A:1023073621589
Marino G, Xu H-K: A general iterative method for nonexpansive mappings in Hilbert spaces. Journal of Mathematical Analysis and Applications 2006, 318(1):43–52. 10.1016/j.jmaa.2005.05.028
Chang S-S, Lee HWJ, Chan CK: A new method for solving equilibrium problem fixed point problem and variational inequality problem with application to optimization. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(9):3307–3319. 10.1016/j.na.2008.04.035
Yao Y, Noor MA, Liou Y-C: On iterative methods for equilibrium problems. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(1):497–509. 10.1016/j.na.2007.12.021
Cho YJ, Qin X: Generalized systems for relaxed cocoercive variational inequalities and projection methods in Hilbert spaces. Mathematical Inequalities & Applications 2009, 12(2):365–375.
Opial Z: Weak convergence of the sequence of successive approximations for nonexpansive mappings. Bulletin of the American Mathematical Society 1967, 73: 591–597. 10.1090/S0002-9904-1967-11761-0
Shimoji K, Takahashi W: Strong convergence to common fixed points of infinite nonexpansive mappings and applications. Taiwanese Journal of Mathematics 2001, 5(2):387–404.
Suzuki T: Strong convergence of Krasnoselskii and Mann's type sequences for one-parameter nonexpansive semigroups without Bochner integrals. Journal of Mathematical Analysis and Applications 2005, 305(1):227–239. 10.1016/j.jmaa.2004.11.017
Xu H-K: Viscosity approximation methods for nonexpansive mappings. Journal of Mathematical Analysis and Applications 2004, 298(1):279–291. 10.1016/j.jmaa.2004.04.059
Acknowledgments
The authors would like to express their thanks to the Faculty of Science KMUTT Research Fund for their financial support. The first author was supported by the Faculty of Applied Liberal Arts RMUTR Research Fund and King Mongkut's Diamond scholarship for fostering special academic skills by KMUTT. The second author was supported by the Thailand Research Fund and the Commission on Higher Education under Grant no. MRG5180034. Moreover, the authors are extremely grateful to the referees for their helpful suggestions that improved the content of the paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Jaiboon, C., Kumam, P. Strong Convergence for Generalized Equilibrium Problems, Fixed Point Problems and Relaxed Cocoercive Variational Inequalities. J Inequal Appl 2010, 728028 (2010). https://doi.org/10.1155/2010/728028
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/728028
 .
.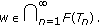
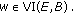 Define,
Define,