- Research Article
- Open access
- Published:
A Hybrid Iterative Scheme for Variational Inequality Problems for Finite Families of Relatively Weak Quasi-Nonexpansive Mappings
Journal of Inequalities and Applications volume 2010, Article number: 724851 (2010)
Abstract
We consider a hybrid projection algorithm basing on the shrinking projection method for two families of relatively weak quasi-nonexpansive mappings. We establish strong convergence theorems for approximating the common fixed point of the set of the common fixed points of such two families and the set of solutions of the variational inequality for an inverse-strongly monotone operator in the framework of Banach spaces. At the end of the paper, we apply our results to consider the problem of finding a solution of the complementarity problem. Our results improve and extend the corresponding results announced by recent results.
1. Introduction
Let  be a Banach space and let
be a Banach space and let  be a nonempty, closed and convex subset of
be a nonempty, closed and convex subset of  . Let
. Let  be an operator. The classical variational inequality problem [1] for
be an operator. The classical variational inequality problem [1] for  is to find
is to find  such that
such that

where  denotes the dual space of
denotes the dual space of  and
and  the generalized duality pairing between
the generalized duality pairing between  and
and  . The set of all solutions of (1.1) is denoted by
. The set of all solutions of (1.1) is denoted by  . Such a problem is connected with the convex minimization problem, the complementarity, the problem of finding a point
. Such a problem is connected with the convex minimization problem, the complementarity, the problem of finding a point  satisfying
satisfying  , and so on. First, we recall that a mapping
, and so on. First, we recall that a mapping  is said to be
is said to be
(i)monotone if  , for all
, for all 
(ii) -inverse-strongly monotone if there exists a positive real number
-inverse-strongly monotone if there exists a positive real number  such that
such that

Let  be the normalized duality mapping from
be the normalized duality mapping from  into
into  given by
given by

It is well known that if  is uniformly convex, then
is uniformly convex, then  is uniformly continuous on bounded subsets of
is uniformly continuous on bounded subsets of  . Some properties of the duality mapping are given in [2–4].
. Some properties of the duality mapping are given in [2–4].
Recall that a mappings  is said to be nonexpansive if
is said to be nonexpansive if

If  is a nonempty closed convex subset of a Hilbert space
is a nonempty closed convex subset of a Hilbert space  and
and  is the metric projection of
is the metric projection of  onto
onto  , then
, then  is a nonexpansive mapping. This fact actually characterizes Hilbert spaces and, consequently, it is not available in more general Banach spaces. In this connection, Alber [5] recently introduced a generalized projection operator
is a nonexpansive mapping. This fact actually characterizes Hilbert spaces and, consequently, it is not available in more general Banach spaces. In this connection, Alber [5] recently introduced a generalized projection operator  in a Banach space
in a Banach space  which is an analogue of the metric projection in Hilbert spaces.
which is an analogue of the metric projection in Hilbert spaces.
Consider the functional  defined by
defined by

for all  , where
, where  is the normalized duality mapping from
is the normalized duality mapping from  to
to  . Observe that, in a Hilbert space
. Observe that, in a Hilbert space  , (1.5) reduces to
, (1.5) reduces to  =
=  for all
for all  . The generalized projection
. The generalized projection  is a mapping that assigns to an arbitrary point
is a mapping that assigns to an arbitrary point  the minimum point of the functional
the minimum point of the functional  , that is,
, that is,  =
=  , where
, where  is the solution to the minimization problem:
is the solution to the minimization problem:

The existence and uniqueness of the operator  follows from the properties of the functional
follows from the properties of the functional  and strict monotonicity of the mapping
and strict monotonicity of the mapping  (see, e.g., [3, 5–7]). In Hilbert spaces,
(see, e.g., [3, 5–7]). In Hilbert spaces,  =
=  . It is obvious from the definition of the function
. It is obvious from the definition of the function  that
that
(1) for all
for all  ,
,
(2) for all
for all  ,
,
(3) for all
for all  ,
,
(4)If  is a reflexive, strictly convex and smooth Banach space, then, for all
is a reflexive, strictly convex and smooth Banach space, then, for all  ,
,

For more detail see [2, 3]. Let  be a closed convex subset of
be a closed convex subset of  , and let
, and let  be a mapping from
be a mapping from  into itself. We denote by
into itself. We denote by  the set of fixed point of
the set of fixed point of  . A point
. A point  in
in  is said to be an asymptotic fixed point of
is said to be an asymptotic fixed point of  [8] if
[8] if  contains a sequence
contains a sequence  which converges weakly to
which converges weakly to  such that
such that  . The set of asymptotic fixed points of
. The set of asymptotic fixed points of  will be denoted by
will be denoted by  . A mapping
. A mapping  from
from  into itself is called relatively nonexpansive [7, 9, 10] if
into itself is called relatively nonexpansive [7, 9, 10] if  =
=  and
and  for all
for all  and
and  . The asymptotic behavior of relatively nonexpansive mappings were studied in [7, 9]. A point
. The asymptotic behavior of relatively nonexpansive mappings were studied in [7, 9]. A point  in
in  is said to be a strong asymptotic fixed point of
is said to be a strong asymptotic fixed point of  if
if  contains a sequence
contains a sequence  which converges strongly to
which converges strongly to  such that
such that  . The set of strong asymptotic fixed points of
. The set of strong asymptotic fixed points of  will be denoted by
will be denoted by  . A mapping
. A mapping  from
from  into itself is called relatively weak nonexpansive if
into itself is called relatively weak nonexpansive if  and
and  for all
for all  and
and  . If
. If  is a smooth strictly convex and reflexive Banach space, and
is a smooth strictly convex and reflexive Banach space, and  is a continuous monotone mapping with
is a continuous monotone mapping with  , then it is proved in [11] that
, then it is proved in [11] that  , for
, for  is relatively weak nonexpansive.
is relatively weak nonexpansive.  is called relatively weak quasi-nonexpansive if
is called relatively weak quasi-nonexpansive if  and
and  for all
for all  and
and  .
.
Remark 1.1.
The class of relatively weak quasi-nonexpansive mappings is more general than the class of relatively weak nonexpansive mappings [7, 9, 12–14] which requires the strong restriction  =
=  .
.
Remark 1.2.
If  is relatively weak quasi-nonexpansive, then using the definition of
is relatively weak quasi-nonexpansive, then using the definition of  (i.e., the same argument as in the proof of [12, page 260]) one can show that
(i.e., the same argument as in the proof of [12, page 260]) one can show that  is closed and convex. It is obvious that relatively nonexpansive mapping is relatively weak nonexpansive mapping. In fact, for any mapping
is closed and convex. It is obvious that relatively nonexpansive mapping is relatively weak nonexpansive mapping. In fact, for any mapping  we have
we have  . Therefore, if
. Therefore, if  is a relatively nonexpansive mapping, then
is a relatively nonexpansive mapping, then  =
=  =
=  .
.
Iiduka and Takahashi [15] introduced the following algorithm for finding a solution of the variational inequality for an  -inverse-strongly monotone mapping
-inverse-strongly monotone mapping  with
with  for all
for all  and
and  in a
in a  -uniformly convex and uniformly smooth Banach space
-uniformly convex and uniformly smooth Banach space  . For an initial point
. For an initial point  , define a sequence
, define a sequence  by
by

where  is the duality mapping on
is the duality mapping on  , and
, and  is the generalized projection of
is the generalized projection of  onto
onto  . Assume that
. Assume that  for some
for some  with
with  where
where  is the 2-uniformly convexity constant of
is the 2-uniformly convexity constant of  . They proved that if
. They proved that if  is weakly sequentially continuous, then the sequence
is weakly sequentially continuous, then the sequence  converges weakly to some element
converges weakly to some element  in
in  where
where  =
=  .
.
The problem of finding a common element of the set of the variational inequalities for monotone mappings in the framework of Hilbert spaces and Banach spaces has been intensively studied by many authors; see, for instance, [16–18] and the references cited therein.
On the other hand, in 2001, Xu and Ori [19] introduced the following implicit iterative process for a finite family of nonexpansive mappings  , with
, with  a real sequence in
a real sequence in  , and an initial point
, and an initial point  :
:

which can be rewritten in the following compact form:

where  (here the
(here the  function takes values in
function takes values in  . They obtained the following result in a real Hilbert space.
. They obtained the following result in a real Hilbert space.
Theorem XO
Let  be a real Hilbert space,
be a real Hilbert space,  a nonempty closed convex subset of
a nonempty closed convex subset of  , and let
, and let  be a finite family of nonexpansive self-mappings on
be a finite family of nonexpansive self-mappings on  such that
such that  . Let
. Let  be a sequence defined by (1.10). If
be a sequence defined by (1.10). If  is chosen so that
is chosen so that  , as
, as  , then
, then  converges weakly to a common fixed point of the family of
converges weakly to a common fixed point of the family of  .
.
On the other hand, Halpern [20] considered the following explicit iteration:

where  is a nonexpansive mapping and
is a nonexpansive mapping and  is a fixed point. He proved the strong convergence of
is a fixed point. He proved the strong convergence of  to a fixed point of
to a fixed point of  provided that
provided that  =
=  , where
, where  .
.
Very recently, Qin et al. [21] proposed the following modification of the Halpern iteration for a single relatively quasi-nonexpansive mapping in a real Banach space. More precisely, they proved the following theorem.
Theorem 1 QCKZ.
Let  be a nonempty and closed convex subset of a uniformly convex and uniformly smooth Banach space
be a nonempty and closed convex subset of a uniformly convex and uniformly smooth Banach space  and
and  a closed and quasi-
a closed and quasi- -nonexpansive mapping such that
-nonexpansive mapping such that  . Let
. Let  be a sequence generated by the following manner:
be a sequence generated by the following manner:

Assume that  satisfies the restriction:
satisfies the restriction:  , then
, then  converges strongly to
converges strongly to  .
.
Motivated and inspired by the above results, Cai and Hu [22] introduced the hybrid projection algorithm to modify the iterative processes (1.10), (1.11), and (1.12) to have strong convergence for a finite family of relatively weak quasi-nonexpansive mappings in Banach spaces. More precisely, they obtained the following theorem.
Theorem CH
Let  be a nonempty and closed convex subset of a uniformly convex and uniformly smooth Banach space
be a nonempty and closed convex subset of a uniformly convex and uniformly smooth Banach space  and
and  be finite family of closed relatively weak quasi-nonexpansive mappings of
be finite family of closed relatively weak quasi-nonexpansive mappings of  into itself with
into itself with  . Assume that
. Assume that  is uniformly continuous for all
is uniformly continuous for all  . Let
. Let  be a sequence generated by the following algorithm:
be a sequence generated by the following algorithm:

Assume that  and
and  are the sequences in
are the sequences in  satisfying
satisfying  and
and  . Then
. Then  converges strongly to
converges strongly to  , where
, where  is the generalized projection from
is the generalized projection from  onto
onto  .
.
Motivated and inspired by Iiduka and Takahashi [15], Xu and Ori [19], Qin et al.[21], and Cai and Hu [22], we introduce a new hybrid projection algorithm basing on the shrinking projection method for two finite families of closed relatively weak quasi-nonexpansive mappings to have strong convergence theorems for approximating the common element of the set of common fixed points of two finite families of such mappings and the set of solutions of the variational inequality for an inverse-strongly monotone operator in the framework of Banach spaces. Our results improve and extend the corresponding results announced by recent results.
2. Preliminaries
A Banach space  is said to be strictly convex if
is said to be strictly convex if  for all
for all  with
with  and
and  . It is also said to be uniformly convex if
. It is also said to be uniformly convex if  for any two sequences
for any two sequences  in
in  such that
such that  and
and  =
=  . Let
. Let  be the unit sphere of
be the unit sphere of  . Then the Banach space
. Then the Banach space  is said to be smooth provided
is said to be smooth provided

exists for each  . It is also said to be uniformly smooth if the limit is attained uniformly for
. It is also said to be uniformly smooth if the limit is attained uniformly for  . It is well know that if
. It is well know that if  is smooth, then the duality mapping
is smooth, then the duality mapping  is single valued. It is also known that if
is single valued. It is also known that if  is uniformly smooth, then
is uniformly smooth, then  is uniformly norm-to-norm continuous on each bounded subset of
is uniformly norm-to-norm continuous on each bounded subset of  . Some properties of the duality mapping have been given in [3, 23–25]. A Banach space
. Some properties of the duality mapping have been given in [3, 23–25]. A Banach space  is said to have Kadec-Klee property if a sequence
is said to have Kadec-Klee property if a sequence  of
of  satisfying that
satisfying that  and
and  , then
, then  . It is known that if
. It is known that if  is uniformly convex, then
is uniformly convex, then  has the Kadec-Klee property; see [3, 23, 25] for more details.
has the Kadec-Klee property; see [3, 23, 25] for more details.
We define the function  which is called the modulus of convexity of
which is called the modulus of convexity of  as following
as following

Then  is said to be
is said to be  -uniformly convex if there exists a constant
-uniformly convex if there exists a constant  such that constant
such that constant  for all
for all  . Constant
. Constant  is called the
is called the  -uniformly convexity constant of
-uniformly convexity constant of  . A 2-uniformly convex Banach space is uniformly convex, see [26, 27] for more details. We know the following lemma of 2-uniformly convex Banach spaces.
. A 2-uniformly convex Banach space is uniformly convex, see [26, 27] for more details. We know the following lemma of 2-uniformly convex Banach spaces.
Let  be a
be a  -uniformly convex Banach, then for all
-uniformly convex Banach, then for all  from any bounded set of
from any bounded set of  and
and  ,
,

where  is the
is the  -uniformly convexity constant of
-uniformly convexity constant of  .
.
Now we present some definitions and lemmas which will be applied in the proof of the main result in the next section.
Lemma 2.2 (Kamimura and Takahashi [30]).
Let  be a uniformly convex and smooth Banach space and let
be a uniformly convex and smooth Banach space and let  ,
,  be two sequences of
be two sequences of  such that either
such that either  or
or  is bounded. If
is bounded. If  , then
, then  .
.
Lemma 2.3 (Alber [5]).
Let  be a nonempty closed convex subset of a smooth Banach space
be a nonempty closed convex subset of a smooth Banach space  and
and  . Then,
. Then,  if and only if
if and only if  for any
for any  .
.
Lemma 2.4 (Alber [5]).
Let  be a reflexive, strictly convex and smooth Banach space, let
be a reflexive, strictly convex and smooth Banach space, let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  and let
and let  . Then
. Then

for all  .
.
Let  be a reflexive strictly convex, smooth and uniformly Banach space and the duality mapping
be a reflexive strictly convex, smooth and uniformly Banach space and the duality mapping  from
from  to
to  . Then
. Then  is also single-valued, one to one, surjective, and it is the duality mapping from
is also single-valued, one to one, surjective, and it is the duality mapping from  to
to  . We need the following mapping
. We need the following mapping  which studied in Alber [5]:
which studied in Alber [5]:

for all  and
and  . Obviously,
. Obviously,  . We know the following lemma.
. We know the following lemma.
Lemma 2.5 (Kamimura and Takahashi [30]).
Let  be a reflexive, strictly convex and smooth Banach space, and let
be a reflexive, strictly convex and smooth Banach space, and let  be as in (2.5). Then
be as in (2.5). Then

for all  and
and  .
.
Lemma 2.6 ([31, Lemma  ]).
]).
Let  be a uniformly convex Banach space and
be a uniformly convex Banach space and  be a closed ball of
be a closed ball of  . Then there exists a continuous strictly increasing convex function
. Then there exists a continuous strictly increasing convex function  with
with  such that
such that

for all  and
and  with
with  .
.
An operator  of
of  into
into  is said to be hemicontinuous if for all
is said to be hemicontinuous if for all  , the mapping
, the mapping  of
of  into
into  defined by
defined by  is continuous with respect to the
is continuous with respect to the  topology of
topology of  . We denote by
. We denote by  the normal cone for
the normal cone for  at a point
at a point  , that is
, that is

Lemma 2.7 (see [32]).
Let  be a nonempty closed convex subset of a Banach space
be a nonempty closed convex subset of a Banach space  and
and  a monotone, hemicontinuous operator of
a monotone, hemicontinuous operator of  into
into  . Let
. Let  be an operator defined as follows:
be an operator defined as follows:

Then  is maximal monotone and
is maximal monotone and  =
= .
.
3. Main Results
In this section, we prove strong convergence theorem which is our main result.
Theorem 3.1.
Let  be a nonempty, closed and convex subset of a 2-uniformly convex and uniformly smooth Banach space
be a nonempty, closed and convex subset of a 2-uniformly convex and uniformly smooth Banach space  , let
, let  be an
be an  -inverse-strongly monotone mapping of
-inverse-strongly monotone mapping of  into
into  with
with  for all
for all  and
and  . Let
. Let  and
and  be two finite families of closed relatively weak quasi-nonexpansive mappings from
be two finite families of closed relatively weak quasi-nonexpansive mappings from  into itself with
into itself with  , where
, where  . Assume that
. Assume that  and
and  are uniformly continuous for all
are uniformly continuous for all  . Let
. Let  be a sequence generated by the following algolithm:
be a sequence generated by the following algolithm:

where  , and
, and  is the normalized duality mapping on
is the normalized duality mapping on  . Assume that
. Assume that  ,
,  and
and  are the sequences in
are the sequences in  satisfying the restrictions:
satisfying the restrictions:
(C1) ;
;
(C2) for some
for some  with
with  , where
, where  is the 2-uniformly convexity constant of
is the 2-uniformly convexity constant of  ;
;
(C3) and if one of the following conditions is satisfied
and if one of the following conditions is satisfied
(a) and
and  and
and
(b) and
and  .
.
Then  converges strongly to
converges strongly to  , where
, where  is the generalized projection from
is the generalized projection from  onto
onto  .
.
Proof.
By the same method as in the proof of Cai and Hu [22], we can show that  is closed and convex. Next, we show
is closed and convex. Next, we show  for all
for all  . In fact,
. In fact,  is obvious. Suppose
is obvious. Suppose  for some
for some  . Then, for all
. Then, for all  , we know from Lemma 2.5 that
, we know from Lemma 2.5 that

Since  and
and  is
is  -inverse-strongly monotone, we have
-inverse-strongly monotone, we have

Therefore, from Lemma 2.1 and the assumption that  for all
for all  and
and  , we obtain that
, we obtain that

Substituting (3.3) and (3.4) into (3.2) and using the condition that  , we get
, we get

Using (3.5) and the convexity of  , for each
, for each  , we obtain
, we obtain

It follows from (3.6) that

So,  . Then by induction,
. Then by induction,  for all
for all  and hence the sequence
and hence the sequence  generated by (3.1) is well defined. Next, we show that
generated by (3.1) is well defined. Next, we show that  is a convergent sequence in
is a convergent sequence in  . From
. From  , we have
, we have

It follows from  for all
for all  that
that

From Lemma 2.4, we have

for each  and for all
and for all  . Therefore, the sequence
. Therefore, the sequence  is bounded. Furthermore, since
is bounded. Furthermore, since  =
=  and
and  =
=  , we have
, we have

This implies that  is nondecreasing and hence
is nondecreasing and hence  exists. Similarly, by Lemma 2.4, we have, for any positive integer
exists. Similarly, by Lemma 2.4, we have, for any positive integer  , that
, that

The existence of  implies that
implies that  as
as  . From Lemma 2.2, we have
. From Lemma 2.2, we have

Hence,  is a Cauchy sequence. Therefore, there exists a point
is a Cauchy sequence. Therefore, there exists a point  such that
such that  as
as 
Now, we will show that  .
.
-
(I)
We first show that
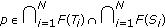 . Indeed, taking
. Indeed, taking 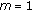 in (3.12), we have
in (3.12), we have

It follows from Lemma 2.2 that

This implies that

The property of the function  implies that
implies that

Since  , we obtain
, we obtain

It follows from the condition (3.14) and (3.17) that

From Lemma 2.2, we have

Combining (3.15) and (3.20), we have

Since  is uniformly norm-to-norm continuous on any bounded sets, we have
is uniformly norm-to-norm continuous on any bounded sets, we have

On the other hand, noticing

Since  is uniformly norm-to-norm continuous on any bounded sets, we have
is uniformly norm-to-norm continuous on any bounded sets, we have

Using (3.15), (3.20), and (3.24) that

Taking the constant  , we have, from Lemma 2.6, that there exists a continuous strictly increasing convex function
, we have, from Lemma 2.6, that there exists a continuous strictly increasing convex function  satisfying the inequality (2.7) and
satisfying the inequality (2.7) and  .
.
Case 1.
Assume that (a) holds. Applying (2.7) and (3.5), we can calculate

This implies that

We observe that

It follows from (3.15), (3.22), (3.23) and (3.25) that

From  and (3.27), we get
and (3.27), we get

By the property of function  , we obtain that
, we obtain that

Since  is uniformly norm-to-norm continuous on any bounded sets, we have
is uniformly norm-to-norm continuous on any bounded sets, we have

From (3.15) and (3.32), we have

Noticing that

for all  . By the uniformly continuity of
. By the uniformly continuity of  , (3.16) and (3.33), we obtain
, (3.16) and (3.33), we obtain

Thus

From the closeness of  , we get
, we get  . Therefore
. Therefore  . In the same manner, we can apply the condition
. In the same manner, we can apply the condition  to conclude that
to conclude that

Again, by (C2) and (3.26), we have

It follows from (3.29) and  that
that

Since  , we have
, we have

From Lemmas 2.4, 2.5, and (3.4), we have

It follows from (3.40) that

Lemma 2.2 implies that

Since  is uniformly norm-to-norm continuous on any bounded sets, we have
is uniformly norm-to-norm continuous on any bounded sets, we have

Combining (3.37) and (3.43), we also obtain

Moreover

By (3.43), (3.15), we have

This implies that

Noticing that

for all  . Since
. Since  is uniformly continuous, we can show that
is uniformly continuous, we can show that  . From the closeness of
. From the closeness of  , we get
, we get  . Therefore
. Therefore  . Hence
. Hence  .
.
Case 2.
Assume that (b) holds. Using the inequalities (2.7) and (3.5), we obtain

This implies that

It follows from (3.21), (3.24) and the condition  that
that

By the property of function  , we obtain that
, we obtain that

Since  is uniformly norm-to-norm continuous on any bounded sets, we have
is uniformly norm-to-norm continuous on any bounded sets, we have

On the other hand, we can calculate

Observe that

It follows from (3.53) and (3.54) that

Applying  and (3.57) and the fact that
and (3.57) and the fact that  is bounded to (3.55), we obtain
is bounded to (3.55), we obtain

From Lemma 2.2, one obtains

We observe that

This together with (3.25) and (3.59), we obtain

Noticing that

for all  . By the uniformly continuity of
. By the uniformly continuity of  , (3.16) and (3.61), we obtain
, (3.16) and (3.61), we obtain

Thus

From the closeness of  , we get
, we get  . Therefore
. Therefore  . By the same proof as in Case 1, we obtain that
. By the same proof as in Case 1, we obtain that

Hence  as
as  for each
for each  and
and

Combining (3.54), (3.61), and (3.65), we also have

Moreover

By (3.43), (3.15), we have

This implies that

Noticing that

for all  . Since
. Since  is uniformly continuous, we can show that
is uniformly continuous, we can show that  . From the closeness of
. From the closeness of  , we get
, we get  . Therefore
. Therefore  . Hence
. Hence  .
.
-
(II)
We next show that
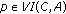 .
.
Let  be an operator defined by:
be an operator defined by:

By Lemma 2.7,  is maximal monotone and
is maximal monotone and  . Let
. Let  , since
, since  , we have
, we have  . From
. From  , we get
, we get

Since  is
is  -inverse-strong monotone, we have
-inverse-strong monotone, we have

On other hand, from  and Lemma 2.3, we have
and Lemma 2.3, we have  , and hence
, and hence

Because  is
is  constricted, it holds from (3.74) and (3.75) that
constricted, it holds from (3.74) and (3.75) that

for all  . By taking the limit as
. By taking the limit as  in (3.76) and from (3.43) and (3.44), we have
in (3.76) and from (3.43) and (3.44), we have  as
as  . By the maximality of
. By the maximality of  we obtain
we obtain  and hence
and hence  . Hence we conclude that
. Hence we conclude that

Finally, we show that  . Indeed, taking the limit as
. Indeed, taking the limit as  in (3.9), we obtain
in (3.9), we obtain

and hence  by Lemma 2.3. This complete the proof.
by Lemma 2.3. This complete the proof.
Remark 3.2.
Theorem 3.1 improves and extends main results of Iiduka and Takahashi [15], Xu and Ori [19], Qin et al. [21], and Cai and Hu [22] because it can be applied to solving the problem of finding the common element of the set of common fixed points of two families of relatively weak quasi-nonexpansive mappings and the set of solutions of the variational inequality for an inverse-strongly monotone operator.
Strong convergence theorem for approximating a common fixed point of two finite families of closed relatively weak quasi-nonexpansive mappings in Banach spaces may not require that  is 2-uniformly convex. In fact, we have the following theorem.
is 2-uniformly convex. In fact, we have the following theorem.
Corollary 3.3.
Let  be a nonempty, closed, and convex subset of a uniformly convex and uniformly smooth Banach space
be a nonempty, closed, and convex subset of a uniformly convex and uniformly smooth Banach space  . Let
. Let  and
and  be two finite families of closed relatively weak quasi-nonexpansive mappings from
be two finite families of closed relatively weak quasi-nonexpansive mappings from  into itself with
into itself with  , where
, where  . Assume that
. Assume that  and
and  are uniformly continuous for all
are uniformly continuous for all  . Let
. Let  be a sequence generated by the following algolithm:
be a sequence generated by the following algolithm:

where  , and
, and  is the normalized duality mapping on
is the normalized duality mapping on  . Assume that
. Assume that  ,
,  and
and  are the sequences in
are the sequences in  satisfying the following restrictions:
satisfying the following restrictions:
(C1)  ;
;
(C2) and if one of the following conditions is satisfied
and if one of the following conditions is satisfied
(a) and
and  and
and
(b) and
and  .
.
Then  converges strongly to
converges strongly to  , where
, where  is the generalized projection from
is the generalized projection from  onto
onto  .
.
Proof.
Put  in Theorem 3.1. Then, we get that
in Theorem 3.1. Then, we get that  . Thus, the method of the proof of Theorem 3.1 gives the required assertion without the requirement that
. Thus, the method of the proof of Theorem 3.1 gives the required assertion without the requirement that  is 2-uniformly convex.
is 2-uniformly convex.
Remark 3.4.
Corollary 3.3 improves Theorem 3.1 of Cai and Hu [22] from a finite family of of relatively weak quasi-nonexpansive mappings to two finite families of relatively weak quasi-nonexpansive mappings.
If  , a Hilbert space, then
, a Hilbert space, then  is
is  -uniformly convex (we can choose
-uniformly convex (we can choose  ) and uniformly smooth real Banach space and closed relatively weak quasi-nonexpansive map reduces to closed weak quasi-nonexpansive map. Furthermore,
) and uniformly smooth real Banach space and closed relatively weak quasi-nonexpansive map reduces to closed weak quasi-nonexpansive map. Furthermore,  , identity operator on
, identity operator on  and
and  , projection mapping from
, projection mapping from  into
into  . Thus, the following corollaries hold.
. Thus, the following corollaries hold.
Corollary 3.5.
Let  be a nonempty, closed and convex subset of a Hilbert space
be a nonempty, closed and convex subset of a Hilbert space  . Let
. Let  and
and  be two finite families of closed weak quasi-nonexpansive mappings from
be two finite families of closed weak quasi-nonexpansive mappings from  into itself with
into itself with  , where
, where  with
with  for all
for all  and
and  . Assume that
. Assume that  and
and  are uniformly continuous for all
are uniformly continuous for all  . Let
. Let  be a sequence generated by the following algorithm:
be a sequence generated by the following algorithm:

where  , and
, and  is the normalized duality mapping on
is the normalized duality mapping on  . Assume that
. Assume that  ,
,  ,
,  ,
,  , and
, and  are the sequences in
are the sequences in  satisfying the restrictions:
satisfying the restrictions:
(C1)  ;
;
(C2)  for some
for some  with
with  , where
, where  is the 2-uniformly convexity constant of
is the 2-uniformly convexity constant of  ;
;
(C3)  and if one of the following conditions is satisfied
and if one of the following conditions is satisfied
(a) and
and  and
and
(b) and
and  .
.
Then  converges strongly to
converges strongly to  , where
, where  is the metric projection from
is the metric projection from  onto
onto  .
.
Let  be a nonempty closed convex cone in
be a nonempty closed convex cone in  , and let
, and let  be an operator from
be an operator from  into
into  . We define its polar in
. We define its polar in  to be the set
to be the set

Then an element  in
in  is called a solution of the complementarity problem if
is called a solution of the complementarity problem if

The set of all solutions of the complementarity problem is denoted by  . Several problem arising in different fields, such as mathematical programming, game theory, mechanics, and geometry, are to find solutions of the complementarity problems.
. Several problem arising in different fields, such as mathematical programming, game theory, mechanics, and geometry, are to find solutions of the complementarity problems.
Theorem 3.6.
Let  be a nonempty, closed and convex subset of a 2-uniformly convex and uniformly smooth Banach space
be a nonempty, closed and convex subset of a 2-uniformly convex and uniformly smooth Banach space  , let
, let  be an
be an  -inverse-strongly monotone mapping of
-inverse-strongly monotone mapping of  into
into  with
with  for all
for all  and
and  . Let
. Let  and
and  be two finite families of closed relatively weak quasi-nonexpansive mappings from
be two finite families of closed relatively weak quasi-nonexpansive mappings from  into itself with
into itself with  , where
, where  . Assume that
. Assume that  and
and  are uniformly continuous for all
are uniformly continuous for all  . Let
. Let  be a sequence generated by the following algorithm:
be a sequence generated by the following algorithm:

where  =
=  =
=  , and
, and  is the normalized duality mapping on
is the normalized duality mapping on  . Assume that
. Assume that  ,
,  and
and  are the sequences in
are the sequences in  satisfying the restrictions:
satisfying the restrictions:
(C1) ;
;
(C2) for some
for some  with
with  , where
, where  is the 2-uniformly convexity constant of
is the 2-uniformly convexity constant of  ;
;
(C3) and if one of the following conditions is satisfied
and if one of the following conditions is satisfied
(a) and
and  and
and
(b) and
and  .
.
Then  converges strongly to
converges strongly to  , where
, where  is the generalized projection from
is the generalized projection from  onto
onto  .
.
Proof.
From [25, Lemma  ], we have
], we have  . From Theorem 3.1, we can obtain the desired conclusion easily.
. From Theorem 3.1, we can obtain the desired conclusion easily.
References
Kinderlehrer D, Stampacchia G: An Introduction to Variational Inequalities and Their Applications, Pure and Applied Mathematics. Volume 88. Academic Press, New York, NY, USA; 1980:xiv+313.
Cioranescu I: Geometry of Banach Spaces, Duality Mappings and Nonlinear Problems, Mathematics and Its Applications. Volume 62. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1990:xiv+260.
Takahashi W: Convex Analysis and Approximation Fixed Points, Mathematical Analysis Series. Volume 2. Yokohama Publishers, Yokohama, Japan; 2000:iv+280.
Vainberg MM: Variational Methods and Method of Monotone Operators. John Wiley & Sons, New York, NY, USA; 1973.
Alber YaI: Metric and generalized projection operators in Banach spaces: properties and applications. In Theory and Applications of Nonlinear Operators of Accretive and Monotone Type, Lecture Notes in Pure and Applied Mathematics. Volume 178. Edited by: Kartsatos AG. Marcel Dekker, New York, NY, USA; 1996:15–50.
Alber YaI, Reich S: An iterative method for solving a class of nonlinear operator equations in Banach spaces. PanAmerican Mathematical Journal 1994, 4(2):39–54.
Butnariu D, Reich S, Zaslavski AJ: Weak convergence of orbIts of nonlinear operators in reflexive Banach spaces. Numerical Functional Analysis and Optimization 2003, 24(5–6):489–508. 10.1081/NFA-120023869
Reich S: A weak convergence theorem for the alternating method with Bregman distances. In Theory and Applications of Nonlinear Operators of Accretive and Monotone Type, Lecture Notes in Pure and Applied Mathematics. Volume 178. Edited by: Kartsatos AG. Marcel Dekker, New York, NY, USA; 1996:313–318.
Butnariu D, Reich S, Zaslavski AJ: Asymptotic behavior of relatively nonexpansive operators in Banach spaces. Journal of Applied Analysis 2001, 7(2):151–174. 10.1515/JAA.2001.151
Censor Y, Reich S: Iterations of paracontractions and firmly nonexpansive operators with applications to feasibility and optimization. Optimization 1996, 37(4):323–339. 10.1080/02331939608844225
Kohsaka F, Takahashi W: Strong convergence of an iterative sequence for maximal monotone operators in a Banach space. Abstract and Applied Analysis 2004, 2004(3):239–249. 10.1155/S1085337504309036
Matsushita S, Takahashi W: A strong convergence theorem for relatively nonexpansive mappings in a Banach space. Journal of Approximation Theory 2005, 134(2):257–266. 10.1016/j.jat.2005.02.007
Plubtieng S, Ungchittrakool K: Strong convergence theorems for a common fixed point of two relatively nonexpansive mappings in a Banach space. Journal of Approximation Theory 2007, 149(2):103–115. 10.1016/j.jat.2007.04.014
Qin X, Su Y: Strong convergence theorems for relatively nonexpansive mappings in a Banach space. Nonlinear Analysis: Theory, Methods & Applications 2007, 67(6):1958–1965. 10.1016/j.na.2006.08.021
Iiduka H, Takahashi W: Weak convergence of a projection algorithm for variational inequalities in a Banach space. Journal of Mathematical Analysis and Applications 2008, 339(1):668–679. 10.1016/j.jmaa.2007.07.019
Browder FE, Petryshyn WV: Construction of fixed points of nonlinear mappings in Hilbert space. Journal of Mathematical Analysis and Applications 1967, 20: 197–228. 10.1016/0022-247X(67)90085-6
Iiduka H, Takahashi W, Toyoda M: Approximation of solutions of variational inequalities for monotone mappings. Panamerican Mathematical Journal 2004, 14(2):49–61.
Liu F, Nashed MZ: Regularization of nonlinear ill-posed variational inequalities and convergence rates. Set-Valued Analysis 1998, 6(4):313–344. 10.1023/A:1008643727926
Xu H-K, Ori RG: An implicit iteration process for nonexpansive mappings. Numerical Functional Analysis and Optimization 2001, 22(5–6):767–773. 10.1081/NFA-100105317
Halpern B: Fixed points of nonexpanding maps. Bulletin of the American Mathematical Society 1967, 73: 957–961. 10.1090/S0002-9904-1967-11864-0
Qin X, Cho YJ, Kang SM, Zhou H: Convergence of a modified Halpern-type iteration algorithm for quasi--nonexpansive mappings. Applied Mathematics Letters 2009, 22(7):1051–1055. 10.1016/j.aml.2009.01.015
Cai G, Hu CS: On the strong convergence of the implicit iterative processes for a finite family of relatively weak quasi-nonexpansive mappings. Applied Mathematics Letters 2010, 23(1):73–78. 10.1016/j.aml.2009.08.006
Cioranescu I: Geometry of Banach Spaces, Duality Mappings and Nonlinear Problems, Mathematics and Its Applications. Volume 62. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1990:xiv+260.
Reich S: Geometry of Banach spaces, duality mappings and nonlinear problems. Bulletin of the American Mathematical Society 1992, 26(2):367–370. 10.1090/S0273-0979-1992-00287-2
Takahashi W: Nonlinear Functional Analysis, Fixed Point Theory and Its Applications. Yokohama Publishers, Yokohama, Japan; 2000:iv+276.
Ball K, Carlen EA, Lieb EH: Sharp uniform convexity and smoothness inequalities for trace norms. Inventiones Mathematicae 1994, 115(3):463–482.
Takahashi Y, Hashimoto K, Kato M: On sharp uniform convexity, smoothness, and strong type, cotype inequalities. Journal of Nonlinear and Convex Analysis 2002, 3(2):267–281.
Beauzamy B: Introduction to Banach Spaces and Their Geometry, North-Holland Mathematics Studies. Volume 68. 2nd edition. North-Holland, Amsterdam, The Netherlands; 1985:xv+338.
Bruck RE, Reich S: Nonexpansive projections and resolvents of accretive operators in Banach spaces. Houston Journal of Mathematics 1977, 3(4):459–470.
Kamimura S, Takahashi W: Strong convergence of a proximal-type algorithm in a Banach space. SIAM Journal on Optimization 2002, 13(3):938–945. 10.1137/S105262340139611X
Cho YJ, Zhou H, Guo G: Weak and strong convergence theorems for three-step iterations with errors for asymptotically nonexpansive mappings. Computers & Mathematics with Applications 2004, 47(4–5):707–717. 10.1016/S0898-1221(04)90058-2
Rockafellar RT: On the maximality of sums of nonlinear monotone operators. Transactions of the American Mathematical Society 1970, 149: 75–88. 10.1090/S0002-9947-1970-0282272-5
Acknowledgments
The first author is supported by grant from under the program Strategic Scholarships for Frontier Research Network for the Ph.D. Program Thai Doctoral degree from the Office of the Higher Education Commission, Thailand and the second author is supported by the Thailand Research Fund under Grant TRG5280011.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kamraksa, U., Wangkeeree, R. A Hybrid Iterative Scheme for Variational Inequality Problems for Finite Families of Relatively Weak Quasi-Nonexpansive Mappings. J Inequal Appl 2010, 724851 (2010). https://doi.org/10.1155/2010/724851
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/724851
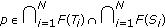 . Indeed, taking
. Indeed, taking 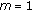 in (3.12), we have
in (3.12), we have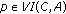 .
.