- Research Article
- Open access
- Published:
Optimal Interior Partial Regularity for Nonlinear Elliptic Systems for the Case 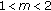 under Natural Growth Condition
under Natural Growth Condition
Journal of Inequalities and Applications volume 2010, Article number: 680714 (2010)
Abstract
We consider the interior regularity for weak solutions of second-order nonlinear elliptic systems with subquadratic growth under natural growth condition. We obtain a general criterion for a weak solution to be regular in the neighborhood of a given point. In particularly the regularity we obtained is optimal.
1. Introduction
In this paper we consider optimal interior partial regularity for the weak solutions of nonlinear elliptic systems with subquadratic growth under natural growth condition of the following type:

where  is a bounded domain in
is a bounded domain in  ,
,  and
and  taking values in
taking values in  , and
, and  has value in
has value in  .
.  ,
,  stand for the
stand for the  of
of  and
and  . To define weak solution to (1.1), one needs to impose certain structural and regularity conditions on
. To define weak solution to (1.1), one needs to impose certain structural and regularity conditions on  and the inhomogeneity
and the inhomogeneity  , as well as to restrict
, as well as to restrict  to a particular class of functions as follows, for
to a particular class of functions as follows, for  ,
,
(E1) are differentiable functions in
are differentiable functions in  and there exists
and there exists  such that
such that

(E2) is uniformly strongly elliptic, that is, for some
is uniformly strongly elliptic, that is, for some  , we have
, we have

(E3) There exists  and
and  monotone nondecreasing such that
monotone nondecreasing such that

for all  , and
, and  ; without loss of generality, we take
; without loss of generality, we take  .
.
Furthermore (E1) allows us to deduce the existence of a function  with
with  for all
for all  such that
such that  is monotone nondecreasing for fixed
is monotone nondecreasing for fixed  ,
,  is concave and monotone nondecreasing for fixed
is concave and monotone nondecreasing for fixed  , and such that for all
, and such that for all  and
and  , we have
, we have

(E4) there exist constants  and
and  , such that
, such that

or
()

Definition 1.1.
By a weak solution of (1.1) with structure assumptions (E1)–(E4) (or (E4 )), we mean a vector valued function
)), we mean a vector valued function  such that
such that

for all  .
.
Even under reasonable assumptions on  and
and  , in the case of systems (i.e.,
, in the case of systems (i.e.,  ) one cannot, in general, expect that weak solutions of (1.1) will be classical, that is,
) one cannot, in general, expect that weak solutions of (1.1) will be classical, that is,  -solutions. This was first shown by De Giorgi [1, 2]. The goal, then, is to establish partial regularity theory. We refer the reader to monographs of Giaquinta [3, 4] for an extensive treatment of partial regularity theory for systems of the form (1.1), as well as more general elliptic systems.
-solutions. This was first shown by De Giorgi [1, 2]. The goal, then, is to establish partial regularity theory. We refer the reader to monographs of Giaquinta [3, 4] for an extensive treatment of partial regularity theory for systems of the form (1.1), as well as more general elliptic systems.
In the class direct proofs, one "freezes the coefficients" with constant coefficients. The solution of the Dirichlet problem associated to these coefficients with boundary data  and the solution itself can then be compared. This procedure was first carried out by Giaquinta and Modica [5].
and the solution itself can then be compared. This procedure was first carried out by Giaquinta and Modica [5].
But the technique of harmonic approximation is to show that a function which is "approximately-harmonic" lies  close to some harmonic function. This technique has its origins in Simon's proof [6] of the regularity theorem of Allard [7]. Which also be used in [8] to find a so-called
close to some harmonic function. This technique has its origins in Simon's proof [6] of the regularity theorem of Allard [7]. Which also be used in [8] to find a so-called  -regularity theorem for energy minimizing harmonic maps. The technique of harmonic approximation allows the author to simplify the original
-regularity theorem for energy minimizing harmonic maps. The technique of harmonic approximation allows the author to simplify the original  -regularity theorem due to Schoen and Uhlenbeck [9].
-regularity theorem due to Schoen and Uhlenbeck [9].
In the remarkable proof when  given by Duzaar and Grotowski in [10], the key difference is that the solution is compared not to the solution of the Dirichlet problem for the system with frozen coefficients, but rather to an A-harmonic function which is close to
given by Duzaar and Grotowski in [10], the key difference is that the solution is compared not to the solution of the Dirichlet problem for the system with frozen coefficients, but rather to an A-harmonic function which is close to  in
in  , where
, where  is a function corresponding from weak solutions. In particular, the optimal regularity result can be obtained. In [11, 12], we deal with the optimal partial regularity of the weak solution to (1.1) for the case
is a function corresponding from weak solutions. In particular, the optimal regularity result can be obtained. In [11, 12], we deal with the optimal partial regularity of the weak solution to (1.1) for the case  by the method of A-harmonic approximation technique, which is advantage to the result of [13]. The extension of A-harmonic approximation technique also can be found in [14, 15].
by the method of A-harmonic approximation technique, which is advantage to the result of [13]. The extension of A-harmonic approximation technique also can be found in [14, 15].
The purpose of this paper is to establish the optimal partial regularity of weak solution to (1.1) under natural growth condition with subquadratic growth, that is, the case of  , directly. Indeed the main difficulty in our setting is that the exponent of the integral function is negative (
, directly. Indeed the main difficulty in our setting is that the exponent of the integral function is negative ( ), which means we cannot use the amplify technique as usually. Motivated by the technique used in [16], where the authors considered the minimizers of nonquadratic functional, we removed the hinder at last. And then with the help of
), which means we cannot use the amplify technique as usually. Motivated by the technique used in [16], where the authors considered the minimizers of nonquadratic functional, we removed the hinder at last. And then with the help of  -harmonic approximation technique, one can find a
-harmonic approximation technique, one can find a  -harmonic function, which is close to a function
-harmonic function, which is close to a function  in sense of
in sense of  , the function
, the function  is which we defined in Lemma 4.2 and which is a corresponding function from the weak solution
is which we defined in Lemma 4.2 and which is a corresponding function from the weak solution  . Thanks to the standard results of linear theory presented in Section 2 and the elementary inequalities, we obtain the decay estimate of
. Thanks to the standard results of linear theory presented in Section 2 and the elementary inequalities, we obtain the decay estimate of

and the optimal regularity. Now we may state the main result.
Theorem 1.2.
Let  be a weak solution of (1.1) with
be a weak solution of (1.1) with  . Suppose that the natural growth conditions (E1)–(E4) (or (E4
. Suppose that the natural growth conditions (E1)–(E4) (or (E4 )) and
)) and  hold. Then there exists
hold. Then there exists  that is open in
that is open in  and
and  for
for  is defined in (E3). Furthermore,
is defined in (E3). Furthermore,

where

In particular,  .
.
2. The  -Harmonic Approximation Technique and Preliminary Lemmas
-Harmonic Approximation Technique and Preliminary Lemmas
In this section, we present the  -harmonic approximation lemma, the key ingredient in proving our regularity result, and some useful preliminaries will be need in later. At first, we introduce two new functions.
-harmonic approximation lemma, the key ingredient in proving our regularity result, and some useful preliminaries will be need in later. At first, we introduce two new functions.
Throughout the paper we will use the functions  and
and  defined by
defined by

for each  and for any
and for any  . From the elementary inequality
. From the elementary inequality

applied to the vector  we deduce that
we deduce that

which immediately yields

The purpose of introducing  is the fact that in contrast to
is the fact that in contrast to  , the function
, the function  is a convex function on
is a convex function on  . This can easily be shown as follows. Firstly a direct computation yields that
. This can easily be shown as follows. Firstly a direct computation yields that  is convex and monotone increasing on
is convex and monotone increasing on  with
with  . Secondly we have
. Secondly we have

for any  .
.
We use a number of properties of  which can be found in [17, Lemma
which can be found in [17, Lemma  ].
].
Lemma 2.1.
Let  and
and  be the functions defined in (2.1). Then for any
be the functions defined in (2.1). Then for any  and
and  there holds:
there holds:
(i)
(ii)
(iii)
(iv)
(v)
(vi) for all
for all with
with 
The inequalities (i)–(iii) also hold if we replace  by
by  .
.
For later purposes we state the following two simple estimates which can easily be deduced from Lemma 2.1(i) and (vi). For  with
with  we have for
we have for  the estimate
the estimate

as for  we have
we have

The next result we would state is the  -harmonic approximation lemma, which is prove in [18].
-harmonic approximation lemma, which is prove in [18].
Lemma 2.2 ( -harmonic approximation lemma).
-harmonic approximation lemma).
Let  be positive constants. Then for any
be positive constants. Then for any  there exist
there exist  with the following property. For any bilinear form
with the following property. For any bilinear form  on
on  which is elliptic in the sense of Legendre-Hadamard with ellipticity constant
which is elliptic in the sense of Legendre-Hadamard with ellipticity constant  and upper bound
and upper bound  , for any
, for any  satisfying
satisfying

for all  , there exists an
, there exists an  -harmonic function
-harmonic function  satisfying
satisfying

Definition 2.3.
Here a function  is called
is called  -harmonic if it satisfies
-harmonic if it satisfies

for all  .
.
Then we would recall a simple consequence of the a prior estimates for solutions of linear elliptic systems of second order with constant coefficients; see [17, Proposition  ] for a similar result.
] for a similar result.
Lemma 2.4.
Let  be such that
be such that

for any  , where
, where  is elliptic in the sense of Legendre-Hadamard with ellipticity constant
is elliptic in the sense of Legendre-Hadamard with ellipticity constant  and upper bound
and upper bound  . Then
. Then  and
and

where the constant  depends only on
depends only on  , and
, and  .
.
The next lemma is a more general version of [17, Lemma  ], which itself is an extension of [3, Lemma
], which itself is an extension of [3, Lemma  , Chapter V]. The proof in which can easily be adapted to the present situation by replacing the condition of homogeneity by Lemma 2.1(ii).
, Chapter V]. The proof in which can easily be adapted to the present situation by replacing the condition of homogeneity by Lemma 2.1(ii).
Lemma 2.5.
Let  , and
, and  be a nonnegative bounded function satisfying
be a nonnegative bounded function satisfying

for all  . Then there exists a constant
. Then there exists a constant  such that
such that

And then we state a Poincare type inequality involving the function  , which have been found in [17] and, in a sharp way, in [18].
, which have been found in [17] and, in a sharp way, in [18].
Lemma 2.6 (Poincare-type inequality).
Let  and
and  , then
, then

where  . In particular, the previous inequality is valid with
. In particular, the previous inequality is valid with  replaced by
replaced by  .
.
We conclude the section with an algebraic fact can be retrieved again from [16], Lemma 2.1.
Lemma 2.7.
For every  and
and  , one has
, one has

for any  , not both zero if
, not both zero if  .
.
3. A Caccioppoli Second Inequality
For  , we define
, we define  and we simply write
and we simply write  .
.
In order to prove the main result, our first aim is to establish a suitable Caccioppoli inequality.
Lemma 3.1 (Caccioppoli second inequality).
Let  be a weak solution of (1.1) with
be a weak solution of (1.1) with  and
and  hold under natural growth conditions (E1)–(E4) (or (E4
hold under natural growth conditions (E1)–(E4) (or (E4 )). Then for every
)). Then for every  , and arbitrary
, and arbitrary  with
with  , one has
, one has

for

where  and the constant
and the constant  .
.
Proof.
Let  . Choose
. Choose  and a standard cut off function
and a standard cut off function  with
with  on
on  , which satisfies
, which satisfies  . For
. For  and
and  , let
, let

and define

Then

and further there holds

Using hypothesis (E2), from Lemma 2.7, and as the elementary inequality

we can get

A simple calculation yields

By (E1), Lemma 2.7 and (3.7), there holds

Noting that supp and
and  , one can take the domain
, one can take the domain  into
into  , and
, and  four parts, and then by Young inequality and the estimations (2.6) and (2.7), thus there is
four parts, and then by Young inequality and the estimations (2.6) and (2.7), thus there is

From the structure condition (E3) yields

Similar to  , we split the domain of integration into four parts as follows. And on the part
, we split the domain of integration into four parts as follows. And on the part  , we see
, we see

as on the set  , there are
, there are

and on the case  , one can get
, one can get

Finally, noting that  , then for the case
, then for the case  , there exists a constant
, there exists a constant  such that
such that

Combining these estimations on  , we have
, we have

for 
And noting that  , and that
, and that  , and similarly as
, and similarly as  , we see
, we see

and for  positive to be fixed later, we have
positive to be fixed later, we have

On the part  , argue anginous as
, argue anginous as  and
and  , by Young's inequality and (2.6) and (2.7), we have
, by Young's inequality and (2.6) and (2.7), we have

Similarly, on the part  , we see
, we see

and on the part  ,
,

and on the part  ,
,

Combining these estimates in  , and noting that
, and noting that  and
and  , we have
, we have

Finally, on  we use Lemma 2.1(iv) and (vi) to bound the integrand of the left-hand side of (3.9) from below:
we use Lemma 2.1(iv) and (vi) to bound the integrand of the left-hand side of (3.9) from below:

Using this in (3.9) together with the estimates  ,
,  ,
,  , and
, and  we finally arrive at
we finally arrive at

The proof is now completed by applying Lemma 2.5.
4. The Proof of the Main Theorem
In this section we proceed to the proof of the partial regularity result and hence consider  to be a weak solution of (1.1). Then we have the following.
to be a weak solution of (1.1). Then we have the following.
Lemma 4.1.
Consider  and
and  with
with  . Furthermore fixed
. Furthermore fixed  in
in  and set
and set  and
and  . Then for the weak solution
. Then for the weak solution  to systems (1.1) with
to systems (1.1) with  and
and  being hold, there holds
being hold, there holds

for  and where one defines
and where one defines

for  and
and 
Proof.
We assume initially that  . Applying Lemma 2.7 and noting that the definition of the weak solution of (1.1), for
. Applying Lemma 2.7 and noting that the definition of the weak solution of (1.1), for  , we deduce
, we deduce

Rearranging this, we find

Using the structure condition (E1) and the estimate (1.5) for the modulus of continuity of  , by Lemma 2.7 and let
, by Lemma 2.7 and let

we can derive

Noting that the estimates (2.6) and (2.7), using first Hölder's inequality and then Jensen's inequality:

here we have used  for
for  .
.
By (E3), Young inequality, (2.6), (2.7), and noting the function  monotone nondecreasing and
monotone nondecreasing and  and that
and that  , we can estimate
, we can estimate  as follows
as follows

for  .
.
Similar to (3.11), to estimate  , one can divide the domain
, one can divide the domain  as previously mentioned. On the set
as previously mentioned. On the set  , for
, for 

while on the part  and noting that
and noting that  ,
,

On 

Finally, on the case  , there exists a constant
, there exists a constant  such that
such that

for 
Whereas, Lemma 2.1 yields

where  is defined in Lemma 3.1.
is defined in Lemma 3.1.
Noting that  , and by Young's inequality, we see
, and by Young's inequality, we see

On  , by (2.7) and Young inequality, we have
, by (2.7) and Young inequality, we have

On the other hand, on  , using (2.6) and Young inequality, we have
, using (2.6) and Young inequality, we have

Thus

Combining these estimates and noting that definition of  , we derive
, we derive

By Lemma 2.6, there is

Combining the above of  with (4.4) and noting the definition of
with (4.4) and noting the definition of  , we can get the lemma immediately.
, we can get the lemma immediately.
We next establish an initial excess-improvement estimate, assuming that the excess  is initially sufficient small. We also define
is initially sufficient small. We also define  , and
, and  , where
, where  stands for the constants
stands for the constants  form Lemma 2.1(vi). The precise statement is the following.
form Lemma 2.1(vi). The precise statement is the following.
Lemma 4.2 (excess-improvement).
Consider weak solution  satisfying the conditions of Theorem 1.2 and
satisfying the conditions of Theorem 1.2 and  fixed in (E3). Then we can find positive constants
fixed in (E3). Then we can find positive constants  , and
, and  and
and  (with
(with  depends only on
depends only on  ,
,  ,
,  ,
,  and
and  and with
and with  ,
,  and
and  depending only on these quantities as well as
depending only on these quantities as well as  ) such that the smallness condition
) such that the smallness condition  :
:

together imply the growth condition

Here one uses the abbreviate  .
.
Proof.
For  to be determined later, we take
to be determined later, we take  to be corresponding constant from the
to be corresponding constant from the  -harmonic approximation lemma, that is, Lemma 2.2, and set
-harmonic approximation lemma, that is, Lemma 2.2, and set

where  stands for the constant
stands for the constant  from Lemma 2.1(vi).
from Lemma 2.1(vi).
Then, from (2.4) and Lemma 2.1(vi), we have

And by Lemma 4.1 and the smallness condition

we can deduce

Inequalities (4.23) and (4.25) fulfill the condition of  -harmonic approximation lemma, which allow us to apply Lemma 2.2. Therefore we can find a function
-harmonic approximation lemma, which allow us to apply Lemma 2.2. Therefore we can find a function  which is
which is  -harmonic such that
-harmonic such that

With the help of Lemma 2.1(iii) and (v), we have

where the constant  depends only on
depends only on  , and
, and  .
.
We proceed to estimate the right-hand side of (4.27). Decomposing  into the set with
into the set with  and that with
and that with  , that using Lemma 2.1(i) and Hölder inequality, we obtain
, that using Lemma 2.1(i) and Hölder inequality, we obtain

where we have abbreviated

Now, since  and
and  is monotone increasing, we deduce from (4.27), also by using Lemma 2.1(i) and (ii), that there holds
is monotone increasing, we deduce from (4.27), also by using Lemma 2.1(i) and (ii), that there holds

where  depends only on
depends only on  , and
, and  . Therefore it remains for us to estimate the quantity
. Therefore it remains for us to estimate the quantity  . By considering the cases
. By considering the cases  and
and  seperately and keeping in mind (4.26), we have (using Lemma 2.1(i)):
seperately and keeping in mind (4.26), we have (using Lemma 2.1(i)):

Using the assumption  and Lemma 2.4, this shows
and Lemma 2.4, this shows

Lemma 3.1 applied on  with
with  , respectively
, respectively  , instead of
, instead of  , respectively,
, respectively,  ; note that the constant
; note that the constant  depends only on
depends only on  :
:

for

Lemma 2.1(iii) yields

where the constant  is given by
is given by  . To estimate the right-hand side of (4.33) we use (2.4), Lemma 2.1(ii) (note that
. To estimate the right-hand side of (4.33) we use (2.4), Lemma 2.1(ii) (note that  ) and (4.26) to infer
) and (4.26) to infer

Using Lemma 2.1(i), Taylor's theorem applied to  on
on  , Lemma 2.4 and (4.31), we obtain
, Lemma 2.4 and (4.31), we obtain

Using the smallness condition  and (4.32) together with the definition of
and (4.32) together with the definition of  yields
yields

Combining all the above estimates with (4.33), and let  for
for  , we get
, we get

where the constant  depends only on
depends only on  , and
, and  (the dependency from
(the dependency from  occurs due to the fact that
occurs due to the fact that  depends on
depends on  ). Choose
). Choose  suitable such that
suitable such that  , and inserting this into (4.30) we easily find (recalling also that
, and inserting this into (4.30) we easily find (recalling also that  ):
):

where the constant  has the same dependencies as
has the same dependencies as  .
.
The regularity result then follows from the fact that this excess-decay estimate for any  in a neighborhood of
in a neighborhood of  . From this estimate we conclude (by Campanato's characterization of Hölder continuous functions [19, 20]) that
. From this estimate we conclude (by Campanato's characterization of Hölder continuous functions [19, 20]) that  has the modulus of continuity
has the modulus of continuity  by a constant times
by a constant times  . By Lemma 2.1(iv) this modulus of continuity carries over to
. By Lemma 2.1(iv) this modulus of continuity carries over to  .
.
References
De Giorgi E: Frontiere orientate dimisura minima. Seminario di Matematica della. Scuola Normale Superiore di Pisa, 1961, Pisa, Italy 1–65.
De Giorgi E: Un esempio di estremali discontinue per un problema variazionale di tipo ellittico. Bollettino della Unione Matematica Italiana 1968, 1: 135–137.
Giaquinta M: Multiple Integrals in the Calculus of Variations and Nonlinear Elliptic Systems, Annals of Mathematics Studies. Volume 105. Princeton University Press, Princeton, NJ, USA; 1983:vii+297.
Giaquinta M: Introduction to Regularity Theory for Nonlinear Elliptic Systems, Lectures in Mathematics ETH Zürich. Birkhäuser, Berlin, Germany; 1993:viii+131.
Giaquinta M, Modica G: Regularity results for some classes of higher order nonlinear elliptic systems. Journal für die Reine und Angewandte Mathematik 1979, 311/312: 145–169.
Simon L: Lectures on Geometric Measure Theory, Proceedings of the Centre for Mathematical Analysis, Australian National University. Volume 3. Australian National University Centre for Mathematical Analysis, Canberra, Australia; 1983:vii+272.
Allard WK: On the first variation of a varifold. Annals of Mathematics 1972, 95: 417–491. 10.2307/1970868
Simon L: Theorems on Regularity and Singularity of Energy Minimizing Maps, Lectures in Mathematics ETH Zürich. Birkhäuser, Basel, Germany; 1996:viii+152.
Schoen R, Uhlenbeck K: A regularity theory for harmonic maps. Journal of Differential Geometry 1982, 17(2):307–335.
Duzaar F, Grotowski JF: Optimal interior partial regularity for nonlinear elliptic systems: the method of -harmonic approximation. Manuscripta Mathematica 2000, 103(3):267–298. 10.1007/s002290070007
Chen S, Tan Z: Optimal interior partial regularity for nonlinear elliptic systems under the natural growth condition: the method of A-harmonic approximation. Acta Mathematica Scientia. Series B 2007, 27(3):491–508. 10.1016/S0252-9602(07)60049-6
Chen S, Tan Z: The method of -harmonic approximation and optimal interior partial regularity for nonlinear elliptic systems under the controllable growth condition. Journal of Mathematical Analysis and Applications 2007, 335(1):20–42. 10.1016/j.jmaa.2007.01.042
Tan Z: -partial regularity for nonlinear elliptic systems. Acta Mathematica Scientia. Series B 1995, 15(3):254–263.
Chen S-H, Tan Z: The method of -harmonic approximation and optimal interior partial regularity for energy minimizing -harmonic maps under the controllable growth condition. Science in China. Series A 2007, 50(1):105–115.
Duzaar F, Mingione G: Regularity for degenerate elliptic problems via -harmonic approximation. Annales de l'Institut Henri Poincaré. Analyse Non Linéaire 2004, 21(5):735–766.
Acerbi E, Fusco N: Regularity for minimizers of nonquadratic functionals: the case . Journal of Mathematical Analysis and Applications 1989, 140(1):115–135. 10.1016/0022-247X(89)90098-X
Carozza M, Fusco N, Mingione G: Partial regularity of minimizers of quasiconvex integrals with subquadratic growth. Annali di Matematica Pura ed Applicata. Serie Quarta 1998, 175: 141–164. 10.1007/BF01783679
Duzaar F, Grotowski JF, Kronz M: Regularity of almost minimizers of quasi-convex variational integrals with subquadratic growth. Annali di Matematica Pura ed Applicata. Series IV 2005, 184(4):421–448. 10.1007/s10231-004-0117-5
Campanato S: Proprietà di una famiglia di spazi funzionali. Annali della Scuola Normale Superiore di Pisa. Classe di Scienze 1964, 18: 137–160.
Campanato S: Equazioni ellittiche del II deg ordine espazi . Annali di Matematica Pura ed Applicata. Serie Quarta 1965, 69: 321–381. 10.1007/BF02414377
Acknowledgments
This work was supported by NCETXMU and the National Natural Science Foundation of China-NSAF (no: 10976026).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chen, S., Tan, Z. Optimal Interior Partial Regularity for Nonlinear Elliptic Systems for the Case 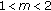 under Natural Growth Condition.
J Inequal Appl 2010, 680714 (2010). https://doi.org/10.1155/2010/680714
under Natural Growth Condition.
J Inequal Appl 2010, 680714 (2010). https://doi.org/10.1155/2010/680714
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/680714
 -Harmonic Approximation Technique and Preliminary Lemmas
-Harmonic Approximation Technique and Preliminary Lemmas