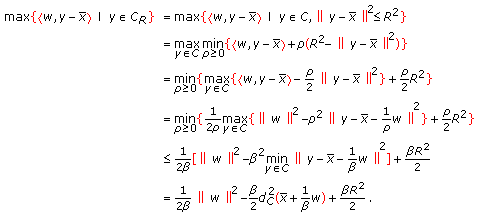- Research Article
- Open access
- Published:
A New Method for Solving Monotone Generalized Variational Inequalities
Journal of Inequalities and Applications volume 2010, Article number: 657192 (2010)
Abstract
We suggest new dual algorithms and iterative methods for solving monotone generalized variational inequalities. Instead of working on the primal space, this method performs a dual step on the dual space by using the dual gap function. Under the suitable conditions, we prove the convergence of the proposed algorithms and estimate their complexity to reach an  -solution. Some preliminary computational results are reported.
-solution. Some preliminary computational results are reported.
1. Introduction
Let  be a convex subset of the real Euclidean space
be a convex subset of the real Euclidean space  ,
,  be a continuous mapping from
be a continuous mapping from  into
into  , and
, and  be a lower semicontinuous convex function from
be a lower semicontinuous convex function from  into
into  . We say that a point
. We say that a point  is a solution of the following generalized variational inequality if it satisfies
is a solution of the following generalized variational inequality if it satisfies

where  denotes the standard dot product in
denotes the standard dot product in  .
.
Associated with the problem (GVI), the dual form of this is expressed as following which is to find  such that
such that

In recent years, this generalized variational inequalities become an attractive field for many researchers and have many important applications in electricity markets, transportations, economics, and nonlinear analysis (see [1–9]).
It is well known that the interior quadratic and dual technique are powerfull tools for analyzing and solving the optimization problems (see [10–16]). Recently these techniques have been used to develop proximal iterative algorithm for variational inequalities (see [17–22]).
In addition Nesterov [23] introduced a dual extrapolation method for solving variational inequalities. Instead of working on the primal space, this method performs a dual step on the dual space.
In this paper we extend results in [23] to the generalized variational inequality problem (GVI) in the dual space. In the first approach, a gap function  is constructed such that
is constructed such that  , for all
, for all  and
and  if and only if
if and only if  solves (GVI). Namely, we first develop a convergent algorithm for (GVI) with
solves (GVI). Namely, we first develop a convergent algorithm for (GVI) with  being monotone function satisfying a certain Lipschitz type condition on
being monotone function satisfying a certain Lipschitz type condition on  . Next, in order to avoid the Lipschitz condition we will show how to find a regularization parameter at every iteration
. Next, in order to avoid the Lipschitz condition we will show how to find a regularization parameter at every iteration  such that the sequence
such that the sequence  converges to a solution of (GVI).
converges to a solution of (GVI).
The remaining part of the paper is organized as follows. In Section 2, we present two convergent algorithms for monotone and generalized variational inequality problems with Lipschitzian condition and without Lipschitzian condition. Section 3 deals with some preliminary results of the proposed methods.
2. Preliminaries
First, let us recall the well-known concepts of monotonicity that will be used in the sequel (see [24]).
Definition 2.1.
Let  be a convex set in
be a convex set in  , and
, and  . The function
. The function  is said to be
is said to be
(i)pseudomonotone on  if
if

(ii)monotone on  if for each
if for each  ,
,

(iii)strongly monotone on  with constant
with constant  if for each
if for each  ,
,

(iv)Lipschitz with constant  on
on  (shortly
(shortly  -Lipschitz), if
-Lipschitz), if

Note that when  is differentiable on some open set containing
is differentiable on some open set containing  , then, since
, then, since  is lower semicontinuous proper convex, the generalized variational inequality (GVI) is equivalent to the following variational inequalities (see [25, 26]):
is lower semicontinuous proper convex, the generalized variational inequality (GVI) is equivalent to the following variational inequalities (see [25, 26]):
Find  such that
such that

Throughout this paper, we assume that:
(A
1
) the interior set of  , int
, int  is nonempty,
is nonempty,
(A
2
) the set  is bounded,
is bounded,
(A
3
) is upper semicontinuous on
is upper semicontinuous on  , and
, and  is proper, closed convex and subdifferentiable on
is proper, closed convex and subdifferentiable on  ,
,
(A
4
) is monotone on
is monotone on  .
.
In special case  , problem (GVI) can be written by the following.
, problem (GVI) can be written by the following.
Find  such that
such that

It is well known that the problem (VI) can be formulated as finding the zero points of the operator  , where
, where

The dual gap function of problem (GVI) is defined as follows:

The following lemma gives two basic properties of the dual gap function (2.7) whose proof can be found, for instance, in [6].
Lemma 2.2.
The function  is a gap function of (GVI), that is,
is a gap function of (GVI), that is,
(i) for all
for all  ,
,
(ii) and
and  if and only if
if and only if  is a solution to (DGVI). Moreover, if
is a solution to (DGVI). Moreover, if  is pseudomonotone then
is pseudomonotone then  is a solution to (DGVI) if and only if it is a solution to (GVI).
is a solution to (DGVI) if and only if it is a solution to (GVI).
The problem  may not be solvable and the dual gap function
may not be solvable and the dual gap function  may not be well-defined. Instead of using gap function
may not be well-defined. Instead of using gap function  , we consider a truncated dual gap function
, we consider a truncated dual gap function  . Suppose that
. Suppose that  fixed and
fixed and  . The truncated dual gap function is defined as follows:
. The truncated dual gap function is defined as follows:

For the following consideration, we define  as a closed ball in
as a closed ball in  centered at
centered at  and radius
and radius  , and
, and  . The following lemma gives some properties for
. The following lemma gives some properties for  .
.
Lemma 2.3.
Under assumptions (A1)–(A4), the following properties hold.
(i)The function  is well-defined and convex on
is well-defined and convex on  .
.
(ii)If a point  is a solution to (DGVI) then
is a solution to (DGVI) then  .
.
(iii)If there exists  such that
such that  and
and  , and
, and  is pseudomonotone, then
is pseudomonotone, then  is a solution to (DGVI) (and also (GVI)).
is a solution to (DGVI) (and also (GVI)).
Proof.
-
(i)
Note that
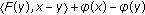 is upper semicontinuous on
is upper semicontinuous on  for
for 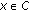 and
and  is bounded. Therefore, the supremum exists which means that
is bounded. Therefore, the supremum exists which means that  is well-defined. Moreover, since
is well-defined. Moreover, since 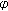 is convex on
is convex on 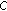 and
and 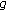 is the supremum of a parametric family of convex functions (which depends on the parameter
is the supremum of a parametric family of convex functions (which depends on the parameter  ), then
), then 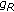 is convex on
is convex on 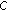
-
(ii)
By definition, it is easy to see that
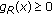 for all
for all 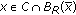 . Let
. Let  be a solution of (DGVI) and
be a solution of (DGVI) and 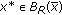 . Then we have
. Then we have 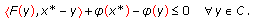 (2.9)
(2.9)
In particular, we have

for all  . Thus
. Thus

this implies  .
.
-
(iii)
For some
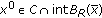 ,
, 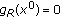 means that
means that  is a solution to (DGVI) restricted to
is a solution to (DGVI) restricted to  . Since
. Since 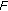 is pseudomonotone,
is pseudomonotone,  is also a solution to (GVI) restricted to
is also a solution to (GVI) restricted to  . Since
. Since  , for any
, for any  , we can choose
, we can choose 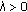 sufficiently small such that
sufficiently small such that 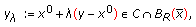 (2.12)
(2.12)

where (2.13) follows from the convexity of  . Since
. Since  , dividing this inequality by
, dividing this inequality by  , we obtain that
, we obtain that  is a solution to (GVI) on
is a solution to (GVI) on  . Since
. Since  is pseudomonotone,
is pseudomonotone,  is also a solution to (DGVI).
is also a solution to (DGVI).
Let  be a nonempty, closed convex set and
be a nonempty, closed convex set and  . Let us denote
. Let us denote  the Euclidean distance from
the Euclidean distance from  to
to  and
and  the point attained this distance, that is,
the point attained this distance, that is,

As usual,  is referred to the Euclidean projection onto the convex set
is referred to the Euclidean projection onto the convex set  . It is well-known that
. It is well-known that  is a nonexpansive and co-coercive operator on
is a nonexpansive and co-coercive operator on  (see [27, 28]).
(see [27, 28]).
The following lemma gives a tool for the next discussion.
Lemma 2.4.
For any  and for any
and for any  , the function
, the function  and the mapping
and the mapping  defined by (2.14) satisfy
defined by (2.14) satisfy



Proof.
Inequality (2.15) is obvious from the property of the projection  (see [27]). Now, we prove the inequality (2.16). For any
(see [27]). Now, we prove the inequality (2.16). For any  , applying (2.15) we have
, applying (2.15) we have

Using the definition of  and noting that
and noting that  and taking minimum with respect to
and taking minimum with respect to  in (2.18), then we have
in (2.18), then we have

which proves (2.16).
From the definition of  , we have
, we have

Since  , applying (2.15) with
, applying (2.15) with  instead of
instead of  and
and  for (2.20), we obtain the last inequality in Lemma 2.4.
for (2.20), we obtain the last inequality in Lemma 2.4.
For a given integer number  , we consider a finite sequence of arbitrary points
, we consider a finite sequence of arbitrary points  , a finite sequence of arbitrary points
, a finite sequence of arbitrary points  and a finite positive sequence
and a finite positive sequence  . Let us define
. Let us define

Then upper bound of the dual gap function  is estimated in the following lemma.
is estimated in the following lemma.
Lemma 2.5.
Suppose that Assumptions (A1)–(A4) are satisfied and

Then, for any  ,
,
(i) , for all
, for all  ,
,  .
.
(ii) .
.
Proof.
-
(i)
We define
 as the Lagrange function of the maximizing problem
as the Lagrange function of the maximizing problem 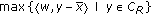 . Using duality theory in convex optimization, then we have
. Using duality theory in convex optimization, then we have 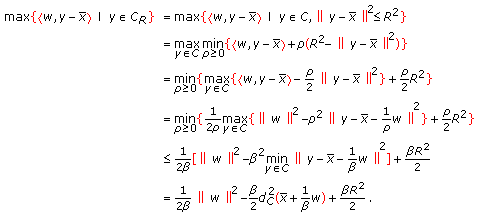 (2.23)
(2.23)
(ii) From the monotonicity of  and (2.22), we have
and (2.22), we have

Combining (2.24), Lemma 2.5(i) and

we get

3. Dual Algorithms
Now, we are going to build the dual interior proximal step for solving (GVI). The main idea is to construct a sequence  such that the sequence
such that the sequence  tends to 0 as
tends to 0 as  . By virtue of Lemma 2.5, we can check whether
. By virtue of Lemma 2.5, we can check whether  is an
is an  -solution to (GVI) or not.
-solution to (GVI) or not.
The dual interior proximal step  at the iteration
at the iteration  is generated by using the following scheme:
is generated by using the following scheme:

where  and
and  are given parameters,
are given parameters,  is the solution to (2.22).
is the solution to (2.22).
The following lemma shows an important property of the sequence  .
.
Lemma 3.1.
The sequence  generated by scheme (3.1) satisfies
generated by scheme (3.1) satisfies

where  ,
,  and
and  . As a consequence, we have
. As a consequence, we have

Proof.
We replace  by
by  and
and  by
by  into (2.16) to obtain
into (2.16) to obtain

Using the inequality (3.4) with  ,
,  ,
,  and noting that
and noting that  , we get
, we get

This implies that

From the subdifferentiability of the convex function  to scheme (3.1), using the first-order necessary optimality condition, we have
to scheme (3.1), using the first-order necessary optimality condition, we have

for all  . This inequality implies that
. This inequality implies that

where  .
.
We apply inequality (3.4) with  ,
,  and
and  and using (3.8) to obtain
and using (3.8) to obtain

Combine this inequality and (3.6), we get

On the other hand, if we denote  , then it follows that
, then it follows that

Combine (3.10) and (3.11), we get

which proves (3.2).
On the other hand, from (3.9) we have

Then the inequality (3.3) is deduced from this inequality and (3.6).
The dual algorithm is an iterative method which generates a sequence  based on scheme (3.1). The algorithm is presented in detail as follows:
based on scheme (3.1). The algorithm is presented in detail as follows:
Algorithm 3.2.
One has the following.
Initialization:
Given a tolerance  , fix an arbitrary point
, fix an arbitrary point  and choose
and choose  ,
,  . Take
. Take  and
and  .
.
Iterations:
For each  , execute four steps below.
, execute four steps below.
Step 1.
Compute a projection point  by taking
by taking

Step 2.
Solve the strongly convex programming problem

to get the unique solution  .
.
Step 3.
Find  such that
such that

Set  .
.
Step 4.
Compute

If  , where
, where  is a given tolerance, then stop.
is a given tolerance, then stop.
Otherwise, increase  by 1 and go back to Step 1.
by 1 and go back to Step 1.
Output:
Compute the final output  as:
as:

Now, we prove the convergence of Algorithm 3.2 and estimate its complexity.
Theorem 3.3.
Suppose that assumptions (A1)–(A3) are satisfied and  is
is  -Lipschitz continuous on
-Lipschitz continuous on  . Then, one has
. Then, one has

where  is the final output defined by the sequence
is the final output defined by the sequence  in Algorithm 3.2. As a consequence, the sequence
in Algorithm 3.2. As a consequence, the sequence  converges to 0 and the number of iterations to reach an
converges to 0 and the number of iterations to reach an  -solution is
-solution is  , where
, where  denotes the largest integer such that
denotes the largest integer such that  .
.
Proof.
From  , where
, where  and
and  , we get
, we get

Substituting (3.20) into (3.2), we obtain

Using this inequality with  for all
for all  and
and  , we obtain
, we obtain

If we choose  for all
for all  in (2.21), then we have
in (2.21), then we have

Hence, from Lemma 2.5(ii), we have

Using inequality (3.22) and  , it implies that
, it implies that

Note that  . It follows from the inequalities (3.24) and (3.25) that
. It follows from the inequalities (3.24) and (3.25) that

which implies that  . The termination criterion at Step 4,
. The termination criterion at Step 4,  , using inequality (2.26) we obtain
, using inequality (2.26) we obtain  and the number of iterations to reach an
and the number of iterations to reach an  -solution is
-solution is  .
.
If there is no the guarantee for the Lipschitz condition, but the sequences  and
and  are uniformly bounded, we suppose that
are uniformly bounded, we suppose that

then the algorithm can be modified to ensure that it still converges. The variant of Algorithm 3.2 is presented as Algorithm 3.4 below.
Algorithm 3.4.
One has the following.
Initialization:
Fix an arbitrary point  and set
and set  . Take
. Take  and
and  . Choose
. Choose  for all
for all  .
.
Iterations:
For each  execute the following steps.
execute the following steps.
Step 1.
Compute the projection point  by taking
by taking

Step 2.
Solve the strong convex programming problem

to get the unique solution  .
.
Step 3.
Find  such that
such that

Set  .
.
Step 4.
Compute

If  , where
, where  is a given tolerance, then stop.
is a given tolerance, then stop.
Otherwise, increase  by 1, update
by 1, update  and go back to Step 1.
and go back to Step 1.
Output:
Compute the final output  as
as

The next theorem shows the convergence of Algorithm 3.4.
Theorem 3.5.
Let assumptions (A1)–(A3) be satisfied and the sequence  be generated by Algorithm 3.4. Suppose that the sequences
be generated by Algorithm 3.4. Suppose that the sequences  and
and  are uniformly bounded by (3.27). Then, we have
are uniformly bounded by (3.27). Then, we have

As a consequence, the sequence  converges to 0 and the number of iterations to reach an
converges to 0 and the number of iterations to reach an  -solution is
-solution is  .
.
Proof.
If we choose  for all
for all  in (2.21), then we have
in (2.21), then we have  . Since
. Since  , it follows from Step 3 of Algorithm 3.4 that
, it follows from Step 3 of Algorithm 3.4 that

From (3.34) and Lemma 2.5(ii), for all  we have
we have

We define  . Then, we have
. Then, we have

We consider, for all 

Then derivative of  is given by
is given by

Thus  is nonincreasing. Combining this with (3.36) and
is nonincreasing. Combining this with (3.36) and  , we have
, we have

From Lemma 3.1,  and
and  , we have
, we have

Combining (3.39) and this inequality, we have

By induction on  , it follows from (3.41) and
, it follows from (3.41) and  that
that

From (3.35) and (3.42), we obtain

which implies that  . The remainder of the theorem is trivially follows from (3.33).
. The remainder of the theorem is trivially follows from (3.33).
4. Illustrative Example and Numerical Results
In this section, we illustrate the proposed algorithms on a class of generalized variational inequalities (GVI), where  is a polyhedral convex set given by
is a polyhedral convex set given by

where  ,
,  . The cost function
. The cost function  is defined by
is defined by

where  ,
,  is a symmetric positive semidefinite matrix and
is a symmetric positive semidefinite matrix and  . The function
. The function  is defined by
is defined by

Then  is subdifferentiable, but it is not differentiable on
is subdifferentiable, but it is not differentiable on  .
.
For this class of problem (GVI) we have the following results.
Lemma 4.1.
Let  . Then
. Then
(i)if  is
is  -strongly monotone on
-strongly monotone on  , then
, then  is monotone on
is monotone on  whenever
whenever  .
.
(ii)if  is
is  -strongly monotone on
-strongly monotone on  , then
, then  is
is  -strongly monotone on
-strongly monotone on  whenever
whenever  .
.
(iii)if  is
is  -Lipschitz on
-Lipschitz on  , then
, then  is
is  -Lipschitz on
-Lipschitz on  .
.
Proof.
Since  is
is  -strongly monotone on
-strongly monotone on  , that is
, that is

we have

Then (i) and (ii) easily follow.
Using the Lipschitz condition, it is not difficult to obtain (iii).
To illustrate our algorithms, we consider the following data.

with  ,
,  ,
,  . From Lemma 4.1, we have
. From Lemma 4.1, we have  is monotone on
is monotone on  . The subproblems in Algorithm 3.2 can be solved efficiently, for example, by using MATLAB Optimization Toolbox R2008a. We obtain the approximate solution
. The subproblems in Algorithm 3.2 can be solved efficiently, for example, by using MATLAB Optimization Toolbox R2008a. We obtain the approximate solution

Now we use Algorithm 3.4 on the same variational inequalities except that

where the  components of the
components of the  are defined by:
are defined by:  , with
, with  randomly chosen in
randomly chosen in  and the
and the  components of
components of  are randomly chosen in
are randomly chosen in  . The function
. The function  is given by Bnouhachem [19]. Under these assumptions, it can be proved that
is given by Bnouhachem [19]. Under these assumptions, it can be proved that  is continuous and monotone on
is continuous and monotone on  .
.
With  and the tolerance
and the tolerance  , we obtained the computational results (see, the Table 1).
, we obtained the computational results (see, the Table 1).
 .
.References
Anh PN, Muu LD, Strodiot J-J: Generalized projection method for non-Lipschitz multivalued monotone variational inequalities. Acta Mathematica Vietnamica 2009, 34(1):67–79.
Anh PN, Muu LD, Nguyen VH, Strodiot JJ: Using the Banach contraction principle to implement the proximal point method for multivalued monotone variational inequalities. Journal of Optimization Theory and Applications 2005, 124(2):285–306. 10.1007/s10957-004-0926-0
Bello Cruz JY, Iusem AN: Convergence of direct methods for paramontone variational inequalities. Computational Optimization and Applications 2010, 46(2):247–263. 10.1007/s10589-009-9246-5
Facchinei F, Pang JS: Finite-Dimensional Variational Inequalities and Complementary Problems. Springer, New York, NY, USA; 2003.
Fukushima M: Equivalent differentiable optimization problems and descent methods for asymmetric variational inequality problems. Mathematical Programming 1992, 53(1):99–110. 10.1007/BF01585696
Konnov IV: Combined Relaxation Methods for Variational Inequalities. Springer, Berlin, Germany; 2000.
Mashreghi J, Nasri M: Forcing strong convergence of Korpelevich's method in Banach spaces with its applications in game theory. Nonlinear Analysis: Theory, Methods & Applications 2010, 72(3–4):2086–2099. 10.1016/j.na.2009.10.009
Noor MA: Iterative schemes for quasimonotone mixed variational inequalities. Optimization 2001, 50(1–2):29–44. 10.1080/02331930108844552
Zhu DL, Marcotte P: Co-coercivity and its role in the convergence of iterative schemes for solving variational inequalities. SIAM Journal on Optimization 1996, 6(3):714–726. 10.1137/S1052623494250415
Daniele P, Giannessi F, Maugeri A: Equilibrium Problems and Variational Models, Nonconvex Optimization and Its Applications. Volume 68. Kluwer Academic Publishers, Norwell, Mass, USA; 2003:xiv+445.
Fang SC, Peterson EL: Generalized variational inequalities. Journal of Optimization Theory and Applications 1982, 38(3):363–383. 10.1007/BF00935344
Goh CJ, Yang XQ: Duality in Optimization and Variational Inequalities, Optimization Theory and Applications. Volume 2. Taylor & Francis, London, UK; 2002:xvi+313.
Iusem AN, Nasri M: Inexact proximal point methods for equilibrium problems in Banach spaces. Numerical Functional Analysis and Optimization 2007, 28(11–12):1279–1308. 10.1080/01630560701766668
Kim JK, Kim KS: New systems of generalized mixed variational inequalities with nonlinear mappings in Hilbert spaces. Journal of Computational Analysis and Applications 2010, 12(3):601–612.
Kim JK, Kim KS: A new system of generalized nonlinear mixed quasivariational inequalities and iterative algorithms in Hilbert spaces. Journal of the Korean Mathematical Society 2007, 44(4):823–834. 10.4134/JKMS.2007.44.4.823
Waltz RA, Morales JL, Nocedal J, Orban D: An interior algorithm for nonlinear optimization that combines line search and trust region steps. Mathematical Programming 2006, 107(3):391–408. 10.1007/s10107-004-0560-5
Anh PN: An interior proximal method for solving monotone generalized variational inequalities. East-West Journal of Mathematics 2008, 10(1):81–100.
Auslender A, Teboulle M: Interior projection-like methods for monotone variational inequalities. Mathematical Programming 2005, 104(1):39–68. 10.1007/s10107-004-0568-x
Bnouhachem A: An LQP method for pseudomonotone variational inequalities. Journal of Global Optimization 2006, 36(3):351–363. 10.1007/s10898-006-9013-4
Iusem AN, Nasri M: Augmented Lagrangian methods for variational inequality problems. RAIRO Operations Research 2010, 44(1):5–25. 10.1051/ro/2010006
Kim JK, Cho SY, Qin X: Hybrid projection algorithms for generalized equilibrium problems and strictly pseudocontractive mappings. Journal of Inequalities and Applications 2010, 2010:-17.
Kim JK, Buong N: Regularization inertial proximal point algorithm for monotone hemicontinuous mapping and inverse strongly monotone mappings in Hilbert spaces. Journal of Inequalities and Applications 2010, 2010:-10.
Nesterov Y: Dual extrapolation and its applications to solving variational inequalities and related problems. Mathematical Programming 2007, 109(2–3):319–344. 10.1007/s10107-006-0034-z
Aubin J-P, Ekeland I: Applied Nonlinear Analysis, Pure and Applied Mathematics. John Wiley & Sons, New York, NY, USA; 1984:xi+518.
Anh PN, Muu LD: Coupling the Banach contraction mapping principle and the proximal point algorithm for solving monotone variational inequalities. Acta Mathematica Vietnamica 2004, 29(2):119–133.
Cohen G: Auxiliary problem principle extended to variational inequalities. Journal of Optimization Theory and Applications 1988, 59(2):325–333.
Mangasarian OL, Solodov MV: A linearly convergent derivative-free descent method for strongly monotone complementarity problems. Computational Optimization and Applications 1999, 14(1):5–16. 10.1023/A:1008752626695
Rockafellar RT: Monotone operators and the proximal point algorithm. SIAM Journal on Control and Optimization 1976, 14(5):877–898. 10.1137/0314056
Acknowledgments
The authors would like to thank the referees for their useful comments, remarks and suggestions. This work was completed while the first author was staying at Kyungnam University for the NRF Postdoctoral Fellowship for Foreign Researchers. And the second author was supported by Kyungnam University Research Fund, 2010.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Anh, P., Kim, J. A New Method for Solving Monotone Generalized Variational Inequalities. J Inequal Appl 2010, 657192 (2010). https://doi.org/10.1155/2010/657192
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/657192
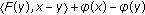 is upper semicontinuous on
is upper semicontinuous on  for
for 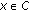 and
and  is bounded. Therefore, the supremum exists which means that
is bounded. Therefore, the supremum exists which means that  is well-defined. Moreover, since
is well-defined. Moreover, since 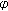 is convex on
is convex on 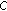 and
and 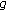 is the supremum of a parametric family of convex functions (which depends on the parameter
is the supremum of a parametric family of convex functions (which depends on the parameter  ), then
), then 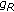 is convex on
is convex on 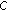
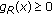 for all
for all 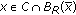 . Let
. Let  be a solution of (DGVI) and
be a solution of (DGVI) and 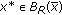 . Then we have
. Then we have 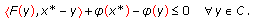
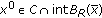 ,
, 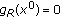 means that
means that  is a solution to (DGVI) restricted to
is a solution to (DGVI) restricted to  . Since
. Since 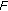 is pseudomonotone,
is pseudomonotone,  is also a solution to (GVI) restricted to
is also a solution to (GVI) restricted to  . Since
. Since  , for any
, for any  , we can choose
, we can choose 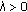 sufficiently small such that
sufficiently small such that 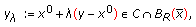
 as the Lagrange function of the maximizing problem
as the Lagrange function of the maximizing problem 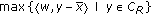 . Using duality theory in convex optimization, then we have
. Using duality theory in convex optimization, then we have