- Research Article
- Open access
- Published:
Weighted Decomposition Estimates for Differential Forms
Journal of Inequalities and Applications volume 2010, Article number: 649340 (2010)
Abstract
After introducing the definition of  -weights, we establish the
-weights, we establish the  -weighted decomposition estimates and
-weighted decomposition estimates and  -weighted Caccioppoli-type estimates for
-weighted Caccioppoli-type estimates for  -harmonic tensors. Furthermore, by Whitney covering lemma, we obtain the global results in domain
-harmonic tensors. Furthermore, by Whitney covering lemma, we obtain the global results in domain  . These results can be used to study the integrability of differential forms and to estimate the integrals for differential forms.
. These results can be used to study the integrability of differential forms and to estimate the integrals for differential forms.
1. Introduction
Let  denote the standard orthogonal basis of
denote the standard orthogonal basis of  . Suppose that
. Suppose that  is the linear space of all
is the linear space of all  -vectors, spanned by the exterior product
-vectors, spanned by the exterior product  corresponding to all ordered
corresponding to all ordered  -tuples
-tuples  ,
,  . Throughout this paper, we always assume that
. Throughout this paper, we always assume that  is an open subset of
is an open subset of  . We use
. We use  to denote the space of all differential
to denote the space of all differential  -forms and
-forms and  to denote the
to denote the  -forms
-forms  on
on  with the coefficient
with the coefficient  for all ordered
for all ordered  -tuples
-tuples  , where
, where  is a manifold. Thus
is a manifold. Thus  is a Banach space with the norm
is a Banach space with the norm

For a differential  -form
-form  , its vector-valued differential form
, its vector-valued differential form  is composed of the differential
is composed of the differential  -form
-form  ,
,  , here the partial derivatives are with respect to the coefficients of
, here the partial derivatives are with respect to the coefficients of  . Usually, suppose that
. Usually, suppose that  is the space consisting of all
is the space consisting of all  , the
, the  th one of
th one of  . We denote the exterior differential operator of
. We denote the exterior differential operator of  -forms by
-forms by  and define the Hodge differential operator
and define the Hodge differential operator  with
with  , where
, where  , and
, and  is the Hodge star operator. We denote a ball or cube by
is the Hodge star operator. We denote a ball or cube by  and the ball or cube with the same center as
and the ball or cube with the same center as  and
and  by
by  . The following nonlinear elliptic equation:
. The following nonlinear elliptic equation:

is called the nonhomogeneous  -harmonic equation of differential forms, where
-harmonic equation of differential forms, where

are operators satisfying the following conditions for almost all  and
and  :
:

where  are two constants, and
are two constants, and  is a fixed exponent dependent on (1.2).
is a fixed exponent dependent on (1.2).
If the operator  in (1.2), it degenerates into the homogeneous
in (1.2), it degenerates into the homogeneous  -harmonic equation
-harmonic equation

The solutions to (1.5) are called  -harmonic tensors. See [1] for the recent research on
-harmonic tensors. See [1] for the recent research on  -harmonic equation.
-harmonic equation.
2. 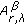 -Weighted Caccioppoli-Type Inequalities
-Weighted Caccioppoli-Type Inequalities
Caccioppoli-type estimates have been widely studied and frequently used in analysis and related fields, including partial differential equations and the theory of elasticity. These inequalities provide upper bounds for the  -norm of
-norm of  if
if  is a function or
is a function or  if
if  is a form with the
is a form with the  -norm of the differential form
-norm of the differential form  . Different versions of the Caccioppoli-type inequality have been established in [2, 3].
. Different versions of the Caccioppoli-type inequality have been established in [2, 3].
We first introduce the following definition of  -weights (or the two-weight), and then establish the local
-weights (or the two-weight), and then establish the local  -weighted Caccioppoli-type inequality for solutions to the homogeneous
-weighted Caccioppoli-type inequality for solutions to the homogeneous  -harmonic equation.
-harmonic equation.
Definition 2.1.
Assume that  and
and  . One says a pair of weights
. One says a pair of weights  satisfies the
satisfies the  -condition, writes
-condition, writes  , if for all balls
, if for all balls  , one has that
, one has that

where  is a constant.
is a constant.
In [4], Nolder obtains the following local Caccioppoli-type estimate.
Lemma 2.2.
Let  be an
be an  -harmonic tensor in
-harmonic tensor in  and let
and let  . Then there exists a constant
. Then there exists a constant  , independent of
, independent of  and
and  , such that
, such that

for all balls or cubes  with
with  and all closed forms
and all closed forms  . Here
. Here  .
.
The next lemma is the generalized Hölder inequality which will be widely used in this paper.
Lemma 2.3.
Let  ,
,  , and
, and  . If
. If  and
and  are measurable functions on
are measurable functions on  , then
, then

for any measurable set  .
.
The following weak reverse Hölder inequality plays an important role in founding the integral estimate of the nonhomogeneous and homogeneous  -harmonic tensor; see [4].
-harmonic tensor; see [4].
Lemma 2.4.
Let  be a solution to (1.2) in
be a solution to (1.2) in  ,
,  and
and  ,
,  . Then there exists a constant
. Then there exists a constant  , depending only on
, depending only on  , and
, and  , such that
, such that

for all balls or cubes  with
with  .
.
The following Whitney covering lemma appears in [4].
Lemma 2.5.
Each  has a modified Whitney cover of cubes
has a modified Whitney cover of cubes  such that
such that

for all  and some
and some  , where
, where  is the characteristic function for a set
is the characteristic function for a set  . Moreover, if
. Moreover, if  , then there exists a cube
, then there exists a cube  (this cube does not need to be a member of
(this cube does not need to be a member of  ) in
) in  such that
such that  .
.
Now we are ready to prove the local weighted Caccioppoli-type inequality for homogeneous  -harmonic tensors.
-harmonic tensors.
Theorem 2.6.
Let  ,
,  , be a solution to the homogeneous
, be a solution to the homogeneous  -harmonic equation (1.5) and
-harmonic equation (1.5) and  for some
for some  and
and  . Then there exists a constant
. Then there exists a constant  , independent of
, independent of  and
and  , such that
, such that

for all balls or cubes  with
with  and all closed forms
and all closed forms  .
.
Specially, if  , one has
, one has

Here  is any constant with
is any constant with  .
.
Proof.
Choosing  and by Lemma 2.3, we have
and by Lemma 2.3, we have

Choosing  and by Lemma 2.2, we know that
and by Lemma 2.2, we know that

where  is a closed form. Putting (2.9) into (2.8), we have
is a closed form. Putting (2.9) into (2.8), we have

Since  is a closed form and
is a closed form and  is a solution to (1.5),
is a solution to (1.5),  is still a solution to (1.5).
is still a solution to (1.5).
When  , taking
, taking  and by Lemma 2.4, we obtain
and by Lemma 2.4, we obtain

By Lemma 2.3, we have

By the condition  , we obtain
, we obtain

where  . By (2.10), (2.11), (2.12), and (2.13), we conclude that
. By (2.10), (2.11), (2.12), and (2.13), we conclude that

Since  , inequality (2.14) can be rewritten as
, inequality (2.14) can be rewritten as

By simple computation, we know that

Then we can change inequality (2.15) into

When  , taking
, taking  and by Lemma 2.4, we obtain
and by Lemma 2.4, we obtain

By Lemma 2.3, it follows that

By (2.10), (2.18), and (2.19), we conclude that

Since  , inequality (2.20) can be rewritten as
, inequality (2.20) can be rewritten as

Because of  , we have that
, we have that

The proof of Theorem 2.6 is completed.
Since there are fore real parameters,  , in Theorem 2.6, we can obtain some desired versions of weighted Caccioppoli-type estimates by different choices of them. Let
, in Theorem 2.6, we can obtain some desired versions of weighted Caccioppoli-type estimates by different choices of them. Let  in Theorem 2.6, we obtain the following corollaries.
in Theorem 2.6, we obtain the following corollaries.
Corollary 2.7.
Let  ,
,  be a solution to the homogeneous
be a solution to the homogeneous  -harmonic equation (1.5) and
-harmonic equation (1.5) and  for some
for some  and
and  . Then there exists a constant
. Then there exists a constant  , independent of
, independent of  and
and  , such that
, such that

for all closed forms  .
.
Furthermore, choosing  in Corollary 2.7, we get the following result.
in Corollary 2.7, we get the following result.
Corollary 2.8.
Let  ,
,  be a solution to the homogeneous
be a solution to the homogeneous  -harmonic equation (1.5) and
-harmonic equation (1.5) and  for some
for some  . Then there exists a constant
. Then there exists a constant  , independent of
, independent of  and
and  , such that
, such that

for all closed forms  .
.
3. The Local Weighted Estimates for the Decomposition
The Hodge decomposition theorem has been playing an important part in partial differential equation, the operator theory, and so on. In the recent years, there are some interesting conclusions on the Hodge decomposition of differential forms; see [5, 6]. In [7], there is the following decomposition theorem for differential form  .
.
Lemma 3.1.
Let  ,
,  ,
,  . Then, there exist differential forms
. Then, there exist differential forms  and
and  , such that
, such that


here  is a positive constant.
is a positive constant.
Definition 3.2.
The weight  satisfies the
satisfies the  -condition on the set
-condition on the set  , write
, write  , if
, if  , a.e., and for all balls
, a.e., and for all balls  , one has that
, one has that

where  .
.
The next lemma states the reverse Hölder inequality for  -weight; see [8].
-weight; see [8].
Lemma 3.3.
Assume that  . Then, there exists a constant
. Then, there exists a constant  , independent of
, independent of  , for all balls
, for all balls  , such that
, such that

where  is a real number.
is a real number.
In this section, we will extend (3.2) to the weighted form.
Theorem 3.4.
Let  be the solution to the nonhomogeneous
be the solution to the nonhomogeneous  -harmonic equation (1.2),
-harmonic equation (1.2),  ,
,  . Then, there exist differential forms
. Then, there exist differential forms  and
and  , such that
, such that


here  ,
,  ,
,  ,
,  , and
, and  is a constant.
is a constant.
Proof.
From (3.2), it follows that


for any  .
.
When  , take
, take  . By Lemma 2.3 with
. By Lemma 2.3 with  and (3.7), we have
and (3.7), we have

Similarly, using Lemma 2.3 and (3.8), we have

Combining (3.9) with (3.10), we have

Take  , then
, then  and
and  . By Lemma 2.4, it follows that
. By Lemma 2.4, it follows that

here  is a constant. Putting (3.11) into (3.12), we get
is a constant. Putting (3.11) into (3.12), we get

By Lemma 2.3, the following inequality holds:

Combining (3.13) with (3.14), we obtain the following estimate:

Since  , we have
, we have

Putting (3.16) into (3.15), we get

Recall that  ,
,  , then we have
, then we have

So (3.17) can be rewritten as

When  , by Lemma 3.3, we know that
, by Lemma 3.3, we know that

where  .
.
Let  , then
, then  and
and  . By Lemma 2.3 with
. By Lemma 2.3 with  and (3.20), we have that
and (3.20), we have that

Similarly, by Lemma 2.3 and (3.20), we have that

Putting (3.7) into (3.21), we have

Putting (3.8) into (3.22), we conclude that

Combining (3.23) with (3.24), we obtain

Let  , then
, then  . By Lemma 2.4, we have
. By Lemma 2.4, we have

where  . Putting (3.26) into (3.25), we get
. Putting (3.26) into (3.25), we get

By Lemma 2.3, we get

Putting (3.28) into (3.27), it follows that

Since  , we have
, we have

Putting (3.30) into (3.29), we get the following inequality:

Since  , (3.31) can be rewritten as
, (3.31) can be rewritten as

So inequality (3.4) is true for  .
.
4. The Global Weighted Estimates
Based on the local weighted estimate for the decomposition and the Whitney covering lemma, we get the global weighted estimate on domain  .
.
Theorem 4.1.
Let  be a differential form satisfying the nonhomogeneous
be a differential form satisfying the nonhomogeneous  -harmonic equation (1.2) in a bounded domain
-harmonic equation (1.2) in a bounded domain  ,
,  ,
,  , and
, and  ,
,  . Then, there exist differential forms
. Then, there exist differential forms  and
and  , such that
, such that

where  and
and  is a constant.
is a constant.
Proof.
By Lemma 2.5,  has a modified Whitney cover of cubes
has a modified Whitney cover of cubes  . Let
. Let  .
.
First, we assume that all cubes  satisfy
satisfy  . By Lemma 2.5 and (3.6), we know that
. By Lemma 2.5 and (3.6), we know that

In the above proof, if there exists one cube  , such that
, such that  can not be contained in
can not be contained in  completely, the proof is as follows. Set
completely, the proof is as follows. Set  , and define
, and define  on
on  as follows:
as follows:

Then, we know that the following formulas are true:

Note that (4.4) hold, and then the following formula is true:

The proof of Theorem 4.1 is completed.
In Theorems 3.4 and 4.1, there is a real parameter  , which makes the results more flexible. By choosing different value of the parameter
, which makes the results more flexible. By choosing different value of the parameter  , we get the estimates in different forms. For example, if we take
, we get the estimates in different forms. For example, if we take  , we have the following corollary.
, we have the following corollary.
Corollary 4.2.
Let  be the solution to the nonhomogeneous
be the solution to the nonhomogeneous  -harmonic equation (1.2),
-harmonic equation (1.2),  ,
,  , and
, and  ,
,  . Then, there exist differential forms
. Then, there exist differential forms  and
and  , such that
, such that

where  is a constant.
is a constant.
References
Wang Y, Wu C: Global Poincaré inequalities for Green's operator applied to the solutions of the nonhomogeneous -harmonic equation. Computers & Mathematics with Applications 2004, 47(10–11):1545–1554. 10.1016/j.camwa.2004.06.006
Ding S: Weighted Caccioppoli-type estimates and weak reverse Hölder inequalities for -harmonic tensors. Proceedings of the American Mathematical Society 1999, 127(9):2657–2664. 10.1090/S0002-9939-99-05285-5
Perić I, Žubrinić D: Caccioppoli's inequality for quasilinear elliptic operators. Mathematical Inequalities and Applications 1999, 2(2):251–261.
Nolder CA: Hardy-Littlewood theorems for -harmonic tensors. Illinois Journal of Mathematics 1999, 43(4):613–631.
Scott C: theory of differential forms on manifolds. Transactions of the American Mathematical Society 1995, 347(6):2075–2096. 10.2307/2154923
Gilbarg D, Trudinger NS: Elliptic Partial Differential Equations of Second Order, Grundlehren der Mathematischen Wissenschaften. Volume 224. 2nd edition. Springer, Berlin, Germany; 1983:xiii+513.
Iwaniec T, Lutoborski A: Integral estimates for null Lagrangians. Archive for Rational Mechanics and Analysis 1993, 125(1):25–79. 10.1007/BF00411477
Garnett JB: Bounded Analytic Functions. Academic Press, New York, NY, USA; 1970.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant no. 10771044) and the Natural Science Foundation of Heilongjiang Province (Grant no. 200605).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, Y., Li, G. Weighted Decomposition Estimates for Differential Forms. J Inequal Appl 2010, 649340 (2010). https://doi.org/10.1155/2010/649340
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/649340
 -Weighted Caccioppoli-Type Inequalities
-Weighted Caccioppoli-Type Inequalities