- Research Article
- Open access
- Published:
Improvement and Reversion of Slater's Inequality and Related Results
Journal of Inequalities and Applications volume 2010, Article number: 646034 (2010)
Abstract
We use an inequality given by Matić and Pečarić (2000) and obtain improvement and reverse of Slater's and related inequalities.
1. Introduction
In 1981 Slater has proved an interesting companion inequality to Jensen's inequality [1].
Theorem 1.1.
Suppose that  is increasing convex function on interval
is increasing convex function on interval  , for
, for  (where
(where  is the interior of the interval
is the interior of the interval  ) and for
) and for  with
with  , if
, if  , then
, then

When  is strictly convex on
is strictly convex on  , inequality (1.1) becomes equality if and only if
, inequality (1.1) becomes equality if and only if  for some
for some  and for all
and for all  with
with  .
.
It was noted in [2] that by using the same proof the following generalization of Slater's inequality (1981) can be given.
Theorem 1.2.
Suppose that  is convex function on interval
is convex function on interval  , for
, for  (where
(where  is the interior of the interval
is the interior of the interval  ) and for
) and for  with
with  . Let
. Let

then inequality (1.1) holds.
When  is strictly convex on
is strictly convex on  , inequality (1.1) becomes equality if and only if
, inequality (1.1) becomes equality if and only if  for some
for some  and for all
and for all  with
with  .
.
Remark 1.3.
For multidimensional version of Theorem 1.2 see [3].
Another companion inequality to Jensen's inequality is a converse proved by Dragomir and Goh in [4].
Theorem 1.4.
Let  be differentiable convex function defined on interval
be differentiable convex function defined on interval  . If
. If  are arbitrary members and
are arbitrary members and  with
with  and let
and let

Then the inequalities

hold.
In the case when  is strictly convex, one has equalities in (1.4) if and only if there is some
is strictly convex, one has equalities in (1.4) if and only if there is some  such that
such that  holds for all
holds for all  with
with 
Matić and Pečarić in [5] proved more general inequality from which (1.1) and (1.4) can be obtained as special cases.
Theorem 1.5.
Let  be differentiable convex function defined on interval
be differentiable convex function defined on interval  and let
and let  and
and  be stated as in Theorem 1.4. If
be stated as in Theorem 1.4. If  is arbitrary chosen number, then one has
is arbitrary chosen number, then one has

Also, when  is strictly convex, one has equality in (1.5) if and only if
is strictly convex, one has equality in (1.5) if and only if  holds for all
holds for all  with
with  .
.
Remark 1.6.
If  and
and  are stated as in Theorem 1.4 and we let
are stated as in Theorem 1.4 and we let  , also if
, also if  , then by setting
, then by setting  in (1.5), we get Slater's inequality (1.1) and similarly by setting
in (1.5), we get Slater's inequality (1.1) and similarly by setting  in (1.5), we get (1.4).
in (1.5), we get (1.4).
The following refinement of (1.4) is also valid [5].
Theorem 1.7.
Let  be strictly convex differentiable function defined on interval
be strictly convex differentiable function defined on interval  and let
and let  and
and  be stated as in Theorem 1.4 and
be stated as in Theorem 1.4 and  , then the inequalities
, then the inequalities


hold.
The equalities hold in (1.6) and in (1.7) if and only if 
Remark 1.8.
In [6] Dragomir has also proved Theorem 1.7.
In this paper, we use an inequality given in [5] and derive two mean value theorems, exponential convexity, log-convexity, and Cauchy means. As applications, such results are also deduce for related inequality. We use some log-convexity criterion and prove improvement and reverse of Slater's and related inequalities. We also prove some determinantal inequalities.
2. Mean Value Theorems
Theorem 2.1.
Let  , where
, where  is closed interval in
is closed interval in  , and let
, and let  ,
,  ,
,  with
with  and
and  . Then there exists
. Then there exists  such that
such that

Proof.
Since  is continuous on
is continuous on  ,
,  for
for  , where
, where  and
and  .
.
Consider the functions  ,
,  defined as
defined as

Since


for  are convex.
are convex.
Now by applying  for
for  in inequality (1.5), we have
in inequality (1.5), we have

From (2.4) we get

and similarly by applying  for
for  in (1.5), we get
in (1.5), we get

Since

by combining (2.5) and (2.6), we have

Now using the fact that for  there exists
there exists  such that
such that  , we get (2.1).
, we get (2.1).
Corollary 2.2.
Let  , where
, where  is closed interval in
is closed interval in  , and let
, and let  , and
, and  be stated as in Theorem 1.4 with
be stated as in Theorem 1.4 with  and
and  . Then there exists
. Then there exists  such that
such that

Proof.
By setting  in Theorem 2.1, we get (2.9).
in Theorem 2.1, we get (2.9).
Theorem 2.3.
Let  , where
, where  is closed interval in
is closed interval in  , and let
, and let  ,
,  and
and  with
with  . Then there exists
. Then there exists  such that
such that

provided that the denominators are nonzero.
Proof.
Let the function  be defined by
be defined by

where  and
and  are defined as
are defined as

Then, using Theorem 2.1 with  , we have
, we have

because  .
.
Since  as
as  and
and  , therefore, (2.13) gives us
, therefore, (2.13) gives us

After putting the values of  and
and  , we get (2.10).
, we get (2.10).
Corollary 2.4.
Let  , where
, where  is closed interval in
is closed interval in  , and
, and  ,
,  and let
and let  ,
,  with
with  . Then there exists
. Then there exists  such that
such that

provided that the denominators are nonzero.
Proof.
By setting  in Theorem 2.3, we get (2.15).
in Theorem 2.3, we get (2.15).
Corollary 2.5.
Let  with
with  and
and  ,
,  . Then for
. Then for  ,
,  , there exists
, there exists  , where
, where  is positive closed interval, such that
is positive closed interval, such that

Proof.
By setting  and
and  ,
,  , in Theorem 2.3, we get (2.16).
, in Theorem 2.3, we get (2.16).
Corollary 2.6.
Let  ,
,  ,
,  and
and  with
with  . Then for
. Then for  ,
,  , there exists
, there exists  , where
, where  is positive closed interval, such that
is positive closed interval, such that

Proof.
By setting  and
and  ,
,  , in (2.15), we get (2.17).
, in (2.15), we get (2.17).
Remark 2.7.
Note that we can consider the interval  , where
, where  ,
, 
Since the function  with
with  is invertible, then from (2.16) we have
is invertible, then from (2.16) we have

We will say that the expression in the middle is a mean of  .
.
From (2.17) we have

The expression in the middle of (2.19) is a mean of  .
.
In fact similar results can also be given for (2.10) and (2.15). Namely, suppose that  has inverse function, then from (2.10) and (2.15) we have
has inverse function, then from (2.10) and (2.15) we have

So, we have that the expression on the right-hand side of (2.20) is also means.
3. Improvements and Related Results
Definition 3.1 (see [7, page 2]).
A function  is convex if
is convex if

holds for every  ,
, 
Lemma 3.2 (see [8]).
Let one define the function

Then  , that is,
, that is,  is convex for
is convex for  .
.
Definition 3.3 (see [9]).
A function  is exponentially convex if it is continuous and
is exponentially convex if it is continuous and

for all  ,
,  and
and  ,
,  such that
such that  or equivalently
or equivalently

Corollary 3.4 (see [9]).
If  is exponentially convex function, then
is exponentially convex function, then

for every 
Corollary 3.5 (see [9]).
If  is exponentially convex function, then
is exponentially convex function, then  is a log-convex function that is
is a log-convex function that is

Theorem 3.6.
Let  ,
,  . Consider
. Consider  to be defined by
to be defined by

Then
(i)for every  and for every
and for every  , the matrix
, the matrix  is a positive semidefinite matrix; particularly
is a positive semidefinite matrix; particularly

(ii)the function  is exponentially convex;
is exponentially convex;
(iii)if  , then the function
, then the function  is log-convex, that is, for
is log-convex, that is, for  , one has
, one has

Proof.

Let us consider the function defined by

where  for all
for all 
Then we have

Therefore,  is convex function for
is convex function for  . Using
. Using  in inequality (1.5), we get
in inequality (1.5), we get

so the matrix  is positive semi-definite.
is positive semi-definite.

Since  and
and  , so
, so  is continuous for all
is continuous for all  and we have exponentially convexity of the function
and we have exponentially convexity of the function  .
.
-
(iii)
Let
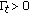 , then by Corollary 3.5 we have that
, then by Corollary 3.5 we have that  is log-convex, that is,
is log-convex, that is, 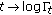 is convex, and by (3.1) for
is convex, and by (3.1) for 
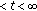 and taking
and taking 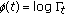 , we get
, we get 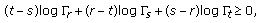 (3.13)
(3.13)
which is equivalent to (3.9).
Corollary 3.7.
Let  ,
,  and
and  . Consider
. Consider  to be defined by
to be defined by

Then
(i)for every  and for every
and for every  , the matrix
, the matrix  is a positive semi-definite matrix. Particularly
is a positive semi-definite matrix. Particularly

(ii)the function  is exponentially convex;
is exponentially convex;
(iii)if  , then the function
, then the function  is log-convex, that is, for
is log-convex, that is, for  , one has
, one has

Proof.
To get the required results, set  in Theorem 3.6.
in Theorem 3.6.
Let  be positive n-tuple and
be positive n-tuple and  positive real numbers, and let
positive real numbers, and let  . Let
. Let  denote the power mean of order
denote the power mean of order  , defined by
, defined by

Let us note that  .
.
By (2.18) we can give the following definition of Cauchy means.
Let  with
with  ,
,  is positive closed interval, and
is positive closed interval, and  ,
, 

for  are means of
are means of  . Moreover we can extend these means to the other cases.
. Moreover we can extend these means to the other cases.
So by limit we have

where  .
.
Theorem 3.8.
Let  such that
such that  , then the following inequality is valid:
, then the following inequality is valid:

Proof.
For convex function  it holds that ([7, page 2])
it holds that ([7, page 2])

with  ,
,  ,
,  ,
,  Since by Theorem 3.6,
Since by Theorem 3.6,  is log-convex, we can set in (3.21):
is log-convex, we can set in (3.21):  ,
,  ,
,  ,
,  , and
, and  , then we get
, then we get

From (3.22) we get (3.20) for  and
and  .
.
For  and
and  we have limiting case.
we have limiting case.
Similarly by (2.19) we can give the following definition of Cauchy type means.
Let  with
with  ,
,  is positive closed interval, and
is positive closed interval, and 

for  are means of
are means of  . Moreover we can extend these means to the other cases.
. Moreover we can extend these means to the other cases.
So by limit we have

where  .
.
Theorem 3.9.
Let  such that
such that  , then the following inequality is valid:
, then the following inequality is valid:

Proof.
The proof is similar to the proof of Theorem 3.8.
Let  be stated as above, define
be stated as above, define  as
as

The following improvement and reverse of Slater's inequality are valid.
Theorem 3.10.
Let  ,
,  . Let
. Let  be defined by
be defined by

Then
-
(i)
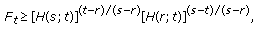 (3.28)
(3.28)
for  and
and  .
.
-
(ii)
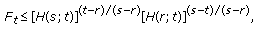 (3.29)
(3.29)
for  .
.
where,

Proof.
-
(i)
By setting
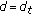 in (3.7),
in (3.7), 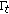 becomes
becomes 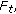 and for
and for 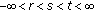 , setting
, setting 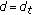 in (3.9), we get
in (3.9), we get 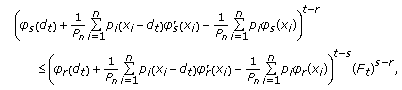 (3.31)
(3.31)
that is,

From (3.32) we get (3.28), and similarly for  (3.9) becomes
(3.9) becomes

by the same process we can get (3.28).
-
(ii)
For
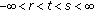 (3.9) becomes
(3.9) becomes 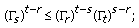 (3.34)
(3.34)
setting  in (3.34), we get (3.29).
in (3.34), we get (3.29).
Theorem 3.11.
Let  ,
,  .
.
Then for every  and for every
and for every  , the matrices
, the matrices  ,
,  are positive semi-definite matrices. Particularly
are positive semi-definite matrices. Particularly


where  is defined by (3.30).
is defined by (3.30).
Proof.
By setting  and
and  in Theorem 3.6(i), we get the required results.
in Theorem 3.6(i), we get the required results.
Remark 3.12.
We note that  . So by setting
. So by setting  in (3.35), we have special case of (3.28) for
in (3.35), we have special case of (3.28) for  , and
, and  if
if  and for
and for  , and
, and  if
if  . Similarly by setting
. Similarly by setting  in (3.36), we have special case of (3.29) for
in (3.36), we have special case of (3.29) for  if
if  and for
and for  if
if  .
.
Let  be stated as above, define
be stated as above, define  as
as

The following improvement and reverse of inequality (1.6) are also valid.
Theorem 3.13.
Let  for all
for all  ,
,  . Let
. Let  be defined by
be defined by

Then
-
(i)
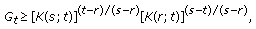 (3.39)
(3.39)
for  and
and  .
.
-
(ii)
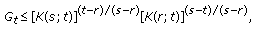 (3.40)
(3.40)
for  ,
,
where

Proof.
-
(i)
By setting
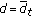 in (3.9), we get (3.39) for
in (3.9), we get (3.39) for 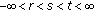 , and similarly we can get (3.39) for the case
, and similarly we can get (3.39) for the case 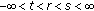 .
. -
(ii)
For
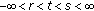 (3.9) becomes
(3.9) becomes  (3.42)
(3.42)
setting  in (3.42), we get (3.40).
in (3.42), we get (3.40).
Theorem 3.14.
Let  ,
,  .
.
Then for every  and for every
and for every  , the matrices
, the matrices  ,
,  are positive semi-definite matrices. Particularly
are positive semi-definite matrices. Particularly


where  is defined by (3.41).
is defined by (3.41).
Proof.
By setting  and
and  in Theorem 3.6(i), we get the required results.
in Theorem 3.6(i), we get the required results.
Remark 3.15.
We note that  . So by setting
. So by setting  in (3.43), we have special case of (3.39) for
in (3.43), we have special case of (3.39) for  if
if  and for
and for  , and
, and  if
if  . Similarly by setting
. Similarly by setting  in (3.44), we have special case of (3.40) for
in (3.44), we have special case of (3.40) for  , and
, and  if
if  and for
and for  , and
, and  if
if  .
.
References
Slater ML: A companion inequality to Jensen's inequality. Journal of Approximation Theory 1981, 32(2):160–166. 10.1016/0021-9045(81)90112-X
Pečarić JE: A companion to Jensen-Steffensen's inequality. Journal of Approximation Theory 1985, 44(3):289–291. 10.1016/0021-9045(85)90099-1
Pečarić JE: A multidimensional generalization of Slater's inequality. Journal of Approximation Theory 1985, 44(3):292–294. 10.1016/0021-9045(85)90100-5
Dragomir SS, Goh CJ: A counterpart of Jensen's discrete inequality for differentiable convex mappings and applications in information theory. Mathematical and Computer Modelling 1996, 24(2):1–11. 10.1016/0895-7177(96)00085-4
Matić M, Pečarić JE: Some companion inequalities to Jensen's inequality. Mathematical Inequalities & Applications 2000, 3(3):355–368.
Dragomir SS: On a converse of Jensen's inequality. Univerzitet u Beogradu. Publikacije Elektrotehničkog Fakulteta. Serija Matematika 2001, 12: 48–51.
Pečarić JE, Proschan F, Tong YL: Convex Functions, Partial Orderings, and Statistical Applications, Mathematics in Science and Engineering. Volume 187. Academic Press, Boston, Mass, USA; 1992:xiv+467.
Anwar M, Pečarić JE: On logarithmic convexity for differences of power means and related results. Journal of Mathematical Inequalities 2009, 4(2):81–90.
Anwar M, Jakšetić JE, Pečarić J, Atiq ur Rehman : Exponential convexity, positive semi-definite matrices and fundamental inequalities. Journal of Mathematical Inequalities 2010, 4(2):171–189.
Acknowledgments
The research of the first and second authors was funded by Higher Education Commission, Pakistan. The research of the second author was supported by the Croatian Ministry of Science, Education, and Sports under the Research Grant 117-1170889-0888.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Adil Khan, M., Pečarić, J. Improvement and Reversion of Slater's Inequality and Related Results. J Inequal Appl 2010, 646034 (2010). https://doi.org/10.1155/2010/646034
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/646034
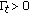 , then by Corollary 3.5 we have that
, then by Corollary 3.5 we have that  is log-convex, that is,
is log-convex, that is, 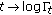 is convex, and by (3.1) for
is convex, and by (3.1) for 
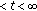 and taking
and taking 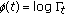 , we get
, we get 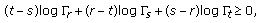
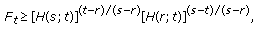
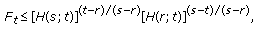
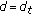 in (3.7),
in (3.7), 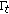 becomes
becomes 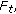 and for
and for 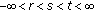 , setting
, setting 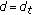 in (3.9), we get
in (3.9), we get 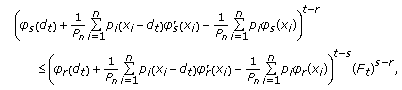
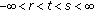 (3.9) becomes
(3.9) becomes 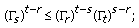
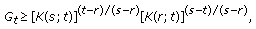
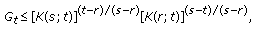
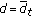 in (3.9), we get (3.39) for
in (3.9), we get (3.39) for 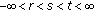 , and similarly we can get (3.39) for the case
, and similarly we can get (3.39) for the case 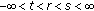 .
.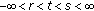 (3.9) becomes
(3.9) becomes 