- Research Article
- Open access
- Published:
New Dilated LMI Characterization for the Multiobjective Full-Order Dynamic Output Feedback Synthesis Problem
Journal of Inequalities and Applications volume 2010, Article number: 608374 (2010)
Abstract
This paper introduces new dilated LMI conditions for continuous-time linear systems which not only characterize stability and  performance specifications, but also,
performance specifications, but also,  performance specifications. These new conditions offer, in addition to new analysis tools, synthesis procedures that have the advantages of keeping the controller parameters independent of the Lyapunov matrix and offering supplementary degrees of freedom. The impact of such advantages is great on the multiobjective full-order dynamic output feedback control problem as the obtained dilated LMI conditions always encompass the standard ones. It follows that much less conservatism is possible in comparison to the currently used standard LMI based synthesis procedures. A numerical simulation, based on an empirically abridged search procedure, is presented and shows the advantage of the proposed synthesis methods.
performance specifications. These new conditions offer, in addition to new analysis tools, synthesis procedures that have the advantages of keeping the controller parameters independent of the Lyapunov matrix and offering supplementary degrees of freedom. The impact of such advantages is great on the multiobjective full-order dynamic output feedback control problem as the obtained dilated LMI conditions always encompass the standard ones. It follows that much less conservatism is possible in comparison to the currently used standard LMI based synthesis procedures. A numerical simulation, based on an empirically abridged search procedure, is presented and shows the advantage of the proposed synthesis methods.
1. Introduction
The impact of linear matrix inequalities on the systems community has been so great that it dramatically changed forever the usually utilized tools for analyzing and synthesizing control systems.The standard LMI conditions benefited greatly from breakthrough advances in convex optimization theory and offered new solutions to many analysis and synthesis problems [1–3]. When necessary and sufficient LMI conditions are not possible, as it is the case for the static output control [4, 5], the multi-objective control [6–8], or the robust control [9–12] problems, sufficient conditions were provided, but were known to be overly conservative. Some dilated versions of LMI conditions have first appeared in the literature in [13], wherein some robust dilated LMI conditions were proposed for some class of matrices. Since then, a flurry of results has been proposed in both the continuous-time [6, 7, 10, 14–17] and the discrete-time systems [5, 14, 18–20]. These conditions offer, though, no particular advantages for monoobjective and precisely known systems, but were found to greatly reduce conservatism in the multi-objective [6–8, 19] and the robust control problems [9, 10, 14–16, 18, 19]. In this respect, an interesting extension for the utilization of these dilated LMI conditions (as in, e.g., [21–23]) provided solutions to the problem of robust root-clustering analysis in some nonconnected regions with respect to polytopic and norm-bounded uncertainties. Generally, the main feature of these LMI conditions, in their dilated versions, consists in the introduction of an instrumental variable giving a suitable structure, from the synthesis viewpoint, in which the controller parameterization is completely independent from the Lyapunov matrix. A particular difficulty though with these proposed dilated versions in the continuous-time case is the absence of dilated  conditions as it is visible in [6, 15].
conditions as it is visible in [6, 15].
This paper introduces new dilated LMIs conditions for the design of full-order dynamic output feedback controllers in continuous-time linear systems, which not only characterize stability and  performance specifications, but also,
performance specifications, but also,  performance specifications as well. Similarly to the existing dilated versions, these new dilated LMI conditions carry the same properties wherein an instrumental variable is introduced giving a suitable structure in which the controller parameterization is completely independent from the Lyapunov matrix. In addition, scalar parameters are also introduced, within these dilated LMI, to provide a supplementary degree of freedom whose impact is to further reduce, in a significant way, the conservatism in sufficient standard LMI conditions. It is also shown, in this paper, that the obtained dilated LMI conditions always encompass the standard ones. As a result, the conservatism which results whenever the standard LMI conditions are used is expected to considerably reduce in many cases. This paper focuses on the multi-objective full-order dynamic output feedback controller design in continuous-time linear systems for which the constraining necessity of using a single Lyapunov matrix to test all the objectives and all the channels, which constitutes a major source of conservatism, is no longer a necessity as a different Lyapunov matrix is separately searched for every objective and for every channel. It is shown, in this paper, that despite constraining the instrumental variable, the new dilated LMI conditions are, at worst, as good as the standard ones, and, generally, much less conservative than the standard LMI conditions. The proposed solution is quite interesting, despite an inevitable increase in the number of decision variables in the involved LMIs and a multivariable search procedure that could be abridged through empirical observations. A numerical simulation is presented and shows the advantage of the proposed synthesis method.
performance specifications as well. Similarly to the existing dilated versions, these new dilated LMI conditions carry the same properties wherein an instrumental variable is introduced giving a suitable structure in which the controller parameterization is completely independent from the Lyapunov matrix. In addition, scalar parameters are also introduced, within these dilated LMI, to provide a supplementary degree of freedom whose impact is to further reduce, in a significant way, the conservatism in sufficient standard LMI conditions. It is also shown, in this paper, that the obtained dilated LMI conditions always encompass the standard ones. As a result, the conservatism which results whenever the standard LMI conditions are used is expected to considerably reduce in many cases. This paper focuses on the multi-objective full-order dynamic output feedback controller design in continuous-time linear systems for which the constraining necessity of using a single Lyapunov matrix to test all the objectives and all the channels, which constitutes a major source of conservatism, is no longer a necessity as a different Lyapunov matrix is separately searched for every objective and for every channel. It is shown, in this paper, that despite constraining the instrumental variable, the new dilated LMI conditions are, at worst, as good as the standard ones, and, generally, much less conservative than the standard LMI conditions. The proposed solution is quite interesting, despite an inevitable increase in the number of decision variables in the involved LMIs and a multivariable search procedure that could be abridged through empirical observations. A numerical simulation is presented and shows the advantage of the proposed synthesis method.
2. Background
Consider the linear time-invariant continuous-time and input-free system

where the state vector  , the perturbation vector
, the perturbation vector  , and the performance vector
, and the performance vector  . All the matrices
. All the matrices  ,
,  ,
,  , and
, and  have appropriate dimensions. Let
have appropriate dimensions. Let  be the system transfer matrix from input
be the system transfer matrix from input  to output
to output  . The following two lemmas are well known (see, e.g., [1, 3]) and provide necessary and sufficient conditions for System (2.1) to be asymptotically stable under an
. The following two lemmas are well known (see, e.g., [1, 3]) and provide necessary and sufficient conditions for System (2.1) to be asymptotically stable under an  performance constraint and a
performance constraint and a  performance constraint, respectively. These standard results will be extensively used in this paper.
performance constraint, respectively. These standard results will be extensively used in this paper.
Lemma 2.1.
System (2.1) with  is asymptotically stable and
is asymptotically stable and  if and only if there exist symmetric matrices
if and only if there exist symmetric matrices  and
and  such that
such that

Lemma 2.2.
System (2.1) is asymptotically stable and  if and only if there exists a symmetric matrix
if and only if there exists a symmetric matrix in
in  such that
such that

3. Multiobjective Control Synthesis
Consider the continuous-time time-invariant linear system with input

where the state vector  ,the perturbation vector
,the perturbation vector  , the input command vector
, the input command vector  , the performance vector
, the performance vector  , and the controlled output vector
, and the controlled output vector  , and all the matrices
, and all the matrices  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  have the appropriate dimensions. In the dynamic output feedback case, the control law is given by the state equations
have the appropriate dimensions. In the dynamic output feedback case, the control law is given by the state equations

As this controller is supposed to be of a full order ,
,  ,
,  , and
, and  . The closed-loop system is then described by the augmented state equations
. The closed-loop system is then described by the augmented state equations

where

The closed loop system transfer matrix from input  to output
to output  then becomes
then becomes

It is supposed that this system is of a multichannel type meaning that the perturbation vector  is partitioned into a given number (say
is partitioned into a given number (say  ) of block components,
) of block components,

and the performance vector  is partitioned into a given number (say
is partitioned into a given number (say  ) of block components,
) of block components,

It is supposed that some performance specifications are defined with respect to a particular channel  (a path relating input component
(a path relating input component  to output component
to output component  ) or a combination of channels. It is also supposed that, for a given control law strategy, these performance specifications can always be expressed in terms of an
) or a combination of channels. It is also supposed that, for a given control law strategy, these performance specifications can always be expressed in terms of an  and/or a
and/or a  transfer matrix norm of the corresponding channel, namely,
transfer matrix norm of the corresponding channel, namely,  , where the matrices
, where the matrices  and
and  are set to select the desired input/output channel from the system closed-loop transfer matrix
are set to select the desired input/output channel from the system closed-loop transfer matrix  . In fact,
. In fact,  is a
is a  -block row matrix of dimension
-block row matrix of dimension  such that only the
such that only the  th block is nonzero and is the identity matrix in
th block is nonzero and is the identity matrix in  . Similarly,
. Similarly,  is an
is an  -block column vector of dimension
-block column vector of dimension  such that only the
such that only the  th block is nonzero and is the identity matrix in
th block is nonzero and is the identity matrix in  . The problem of the multi-objective controller synthesis is to construct a controller that stabilizes the closed loop system and, simultaneously, achieves all the prescribed specifications. It is easy to see that, for each channel
. The problem of the multi-objective controller synthesis is to construct a controller that stabilizes the closed loop system and, simultaneously, achieves all the prescribed specifications. It is easy to see that, for each channel  , the closed loop transfer matrix is given by
, the closed loop transfer matrix is given by

On the channel basis, the closed-loop system is then described by

where

The dynamic output feedback synthesis multi-objective problem consists of looking for a dynamic controller that stabilizes the closed loop system and, in the same time, achieves the desired  and/or
and/or  performance specifications for every single system channel. More specifically, the dynamic output feedback synthesis multi-objective problem aims at making System (3.1) possess the following propriety.
performance specifications for every single system channel. More specifically, the dynamic output feedback synthesis multi-objective problem aims at making System (3.1) possess the following propriety.
Propriety P
System (3.1) is stabilizable by a dynamic output feedback law (3.2) such that, for every channel  , either or both of the following two conditions hold:
, either or both of the following two conditions hold:
 with
with  ;
;
 .
.
Theorem 3.1 (the standard sufficient conditions).
If there exist symmetric matrices  and
and  , general matrices
, general matrices  ,
,  , and
, and  and, for every channel ij, there exists a symmetric matrix
and, for every channel ij, there exists a symmetric matrix  such that either or both of the following two conditions are satisfied:
such that either or both of the following two conditions are satisfied:
[StdH2]

[StdH∞]

then, Propriety  holds, and furthermore, a set of the controller parameters defined in (3.2) is given by
holds, and furthermore, a set of the controller parameters defined in (3.2) is given by

where the nonsingular matrices  and
and  are obtained via the equation
are obtained via the equation

Proof.
If either or both of conditions [StdH2] and [StdH∞] are satisfied, let  and let
and let  be a nonsingular transformation matrix, with
be a nonsingular transformation matrix, with  and
and  selected from (3.14) (among infinitely many possibilities) via the singular value decomposition of
selected from (3.14) (among infinitely many possibilities) via the singular value decomposition of  . In view of (3.13) and (3.14), the following useful identities are easily derived:
. In view of (3.13) and (3.14), the following useful identities are easily derived:

As either or both of conditions [StdH2] and [StdH∞] are satisfied, by the congruence lemma applied to each LMI and in view of the identities listed just above, either or both of the following conditions are also satisfied, respectively,
-
(i)
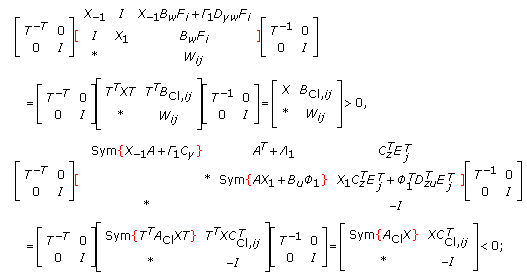 (3.16)
(3.16)
-
(ii)
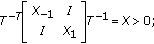 (3.17)
(3.17)

According to Lemmas 2.1 and 2.2, these are precisely the sufficient standard LMI conditions, expressed on a channel basis, for Propriety  to hold.
to hold.
Theorem 3.1 provides sufficient conditions for the existence of a single multi-objective dynamic output controller in terms of LMI conditions in which common Lyapunov matrices are enforced for convexity. This is known to produce, in general, overly conservative results. The following theorem attempts at reducing the effect of this limitation.
Theorem 3.2 (the dilated sufficient conditions).
If there exist general matrices  ,
,  ,
,  ,
,  ,
,  , and
, and  and for every channel ij, for some scalars
and for every channel ij, for some scalars  and
and  , there exist symmetric matrices
, there exist symmetric matrices  ,
,  ,
,  ,
,  ,
,  , general matrices
, general matrices  and
and  such that either or both of the following two conditions are satisfied:
such that either or both of the following two conditions are satisfied:
(i)[DilH2]

(ii)[DilH∞]

Then, Propriety P holds, and furthermore, a set of the controller parameters defined in (3.2) is given by

where the nonsingular matrices  and
and  are obtained via the equation
are obtained via the equation

Proof.
If either or both of conditions [DilH2] and [DilH∞] are satisfied, let  and let
and let  be a nonsingular transformation matrix with
be a nonsingular transformation matrix with  and
and  selected from (3.22) (among infinitely many possibilities) via the singular value decomposition of
selected from (3.22) (among infinitely many possibilities) via the singular value decomposition of  . In view of (3.21) and (3.22), the following useful identities are easily derived:
. In view of (3.21) and (3.22), the following useful identities are easily derived:

On the other hand, let us introduce

As either or both of conditions [DilH2] and [DilH∞] are satisfied, by the congruence Lemma applied to each LMI and in view of the identities listed just above, either or both of the following conditions are also satisfied, respectively.
-
(i)
 (3.25)
(3.25)
-
(ii)
 (3.26)
(3.26)
To summarize, we have proven that if either or both conditions [DilH2] and [DilH∞] are satisfied, then either or both of the following conditions are also satisfied:
-
(i)
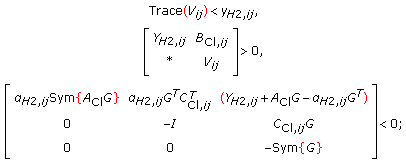 (3.27)
(3.27)
-
(ii)
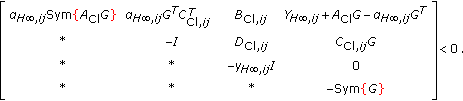 (3.28)
(3.28)
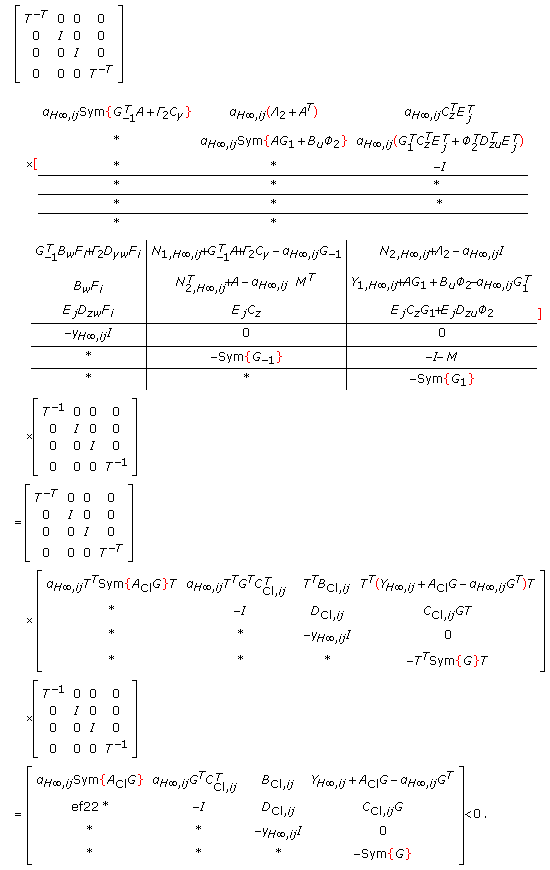
The third LMI of the first item condition is equivalent to

which, according to the elimination lemma [3], leads to

The two previous LMIs are equivalent to  and
and  , that is, for any
, that is, for any  ,
,  .
.
Similarly, the LMI of the second item condition is equivalent to

According to the Elimination lemma, this leads to

The previous two matrix inequalities are equivalent to

Via the Schur lemma, the latter inequality is equivalent to  and
and

Clearly, as  , there always exists a sufficiently large
, there always exists a sufficiently large  which satisfies this LMI. According to Lemmas 2.1 and 2.2, these are precisely the sufficient standard LMI conditions, expressed on a channel basis, for Propriety
which satisfies this LMI. According to Lemmas 2.1 and 2.2, these are precisely the sufficient standard LMI conditions, expressed on a channel basis, for Propriety  to hold.
to hold.
Theorem 3.2 also provides sufficient conditions for the existence of a single multi-objective dynamic output controller in terms of LMI conditions in which the constraint of a common Lyapunov matrix is no longer needed. Convexity is rather insured by constraining the instrumental variables  to be common. This is known to produce, in general, less conservative results than those obtained with the standard conditions of Theorem 3.1. Reducing further this conservatism is also possible through the positive scalar parameters
to be common. This is known to produce, in general, less conservative results than those obtained with the standard conditions of Theorem 3.1. Reducing further this conservatism is also possible through the positive scalar parameters  and
and  . A simple multidimensional search procedure can be carried out in the space of these parameters in order to obtain the values of these parameters for which LMI (3.19) and/or LMI (3.20) are feasible and produce the best multi-objective dynamic output controller with optimal performance levels. This multidimensional search procedure can, however, be overly expensive if the number of channel gets larger. A solution to this rather annoying limitation will be proposed in the next section. Yet, the important results of Theorem 3.2 constitute a significant contribution to the multi-objective control problem.
. A simple multidimensional search procedure can be carried out in the space of these parameters in order to obtain the values of these parameters for which LMI (3.19) and/or LMI (3.20) are feasible and produce the best multi-objective dynamic output controller with optimal performance levels. This multidimensional search procedure can, however, be overly expensive if the number of channel gets larger. A solution to this rather annoying limitation will be proposed in the next section. Yet, the important results of Theorem 3.2 constitute a significant contribution to the multi-objective control problem.
Next, the important question on whether or not the standard conditions could possibly be recovered by the dilated conditions will be addressed in the following section.
4. Recovery Condition
In the following theorem, it will be shown that our proposed dilated LMI conditions for the design of multiobjective full-order dynamic output feedback controllers do indeed encompass the standard conditions. This situation will be of great importance, as it will guarantee that conservatism will be almost always reduced. Similar results do exist in the literature in both the discrete-time [19] and the continuous-time case [6, 7]. The continuous-time results were, however, strictly concerned with the multi-channel  synthesis problem and only in [7] that the recovery of the standard approach is proven. In view of this, the following theorem extends the discrete-time results to the continuous-time case. This point constitutes the major contribution of this paper.
synthesis problem and only in [7] that the recovery of the standard approach is proven. In view of this, the following theorem extends the discrete-time results to the continuous-time case. This point constitutes the major contribution of this paper.
Theorem 4.1.
For, the multi-objective dynamic output feedback synthesis problem, if the standard LMI conditions of Theorem 3.1 are satisfied and achieve, with a given controller, the upper bounds  and
and  , then the dilated inequality conditions of Theorem 3.2 are also satisfied with the same controller and with the upper bounds
, then the dilated inequality conditions of Theorem 3.2 are also satisfied with the same controller and with the upper bounds  and
and  .
.
Proof.
If the standard LMI conditions of Theorem 3.1 are satisfied for a given controller and achieve, for every channel, the upper bounds  and
and  , then there exist symmetric matrices
, then there exist symmetric matrices  and
and  such that
such that

and/or

Let us prove that these standard LMI conditions imply that the dilated inequality conditions of Theorem 3.2 are also satisfied with the same controller. When expressed in terms of the system closed-loop parameters, the right-hand sides of the dilated LMI conditions of Theorem 3.2 take the following form:

and/or

Let, in these matrices,  ,
,  ,
,  ,
,  ,
,  and
and  , these right-hand sides become
, these right-hand sides become

and/or

Let us prove, for these four matrices above, that the second matrix is positive definite while the third and/or the fourth matrices are both negative definite. Clearly, the standard conditions imply that

By virtue of the Schur complement lemma, the third matrix and/or the fourth matrix will be negative definite if and only if  ,
,

and/or

As, from the standard  and
and  conditions,
conditions,

there always exists an  which achieves, simultaneously, these two conditions. As a result, the dilated inequality conditions of Theorem 3.2 are also satisfied. This proves that the dilated LMI multi-objective conditions always encompass the standard ones. Clearly, this means that the dilated-based approach yields upper bounds that are always
which achieves, simultaneously, these two conditions. As a result, the dilated inequality conditions of Theorem 3.2 are also satisfied. This proves that the dilated LMI multi-objective conditions always encompass the standard ones. Clearly, this means that the dilated-based approach yields upper bounds that are always  and
and  .
.
Theorem 4.1 has proven that the dilated LMI conditions of Theorem 3.2 do indeed encompass the standard ones of Theorem 3.1. The multidimensional search procedure carried out in the space of the scalars  being exhaustive, up to a given discretization step that could be made as small as needed, does indeed cover every region, and in particular, the region where the standard conditions are recovered and which is defined by
being exhaustive, up to a given discretization step that could be made as small as needed, does indeed cover every region, and in particular, the region where the standard conditions are recovered and which is defined by  , where
, where  is greater than a minimum value
is greater than a minimum value  defined by the two LMIs just in the proof above. In practice, the value of
defined by the two LMIs just in the proof above. In practice, the value of  can be easily computed through a simple one dimensional line search procedure over these two LMIs.
can be easily computed through a simple one dimensional line search procedure over these two LMIs.
On the other hand, at the light of the results of Theorem 3.2, a controller which achieves the best global performance level can be obtained through the minimization of the global objective function  .Under this setting, it appears that optimality is always achieved very close to where all the
.Under this setting, it appears that optimality is always achieved very close to where all the  and all the
and all the  coincide. This purely empirical rule,observed with many examples we have tried, fits nicely to where the recovery of the standard conditions can be proved. In order to achieve optimality, it is then reasonable to abridge the costly multi-dimensional search procedure to a much cheaper one-dimensional search in the line
coincide. This purely empirical rule,observed with many examples we have tried, fits nicely to where the recovery of the standard conditions can be proved. In order to achieve optimality, it is then reasonable to abridge the costly multi-dimensional search procedure to a much cheaper one-dimensional search in the line  for all channels. In this way, this proposed simple line search procedure not only provides a near optimal solution, but achieves the recovery condition which guarantees that this solution is, at least, as good as the one provided by the standard conditions.
for all channels. In this way, this proposed simple line search procedure not only provides a near optimal solution, but achieves the recovery condition which guarantees that this solution is, at least, as good as the one provided by the standard conditions.
5. An Example
Consider the LTI unstable third-order plant

The system is supposed to be consisting of two channels. Channel 1 connects the perturbation vector  to the performance component
to the performance component  , while Channel 2 connects the perturbation vector
, while Channel 2 connects the perturbation vector  to the performance component
to the performance component  . The objective here is to find a stabilizing full-order (i.e., a third order) dynamic output feedback controller which achieves simultaneously and optimally the performance specifications
. The objective here is to find a stabilizing full-order (i.e., a third order) dynamic output feedback controller which achieves simultaneously and optimally the performance specifications  and
and  , relatively to Channel 2 and Channel 1, respectively. Optimality is here defined as the minimization of
, relatively to Channel 2 and Channel 1, respectively. Optimality is here defined as the minimization of  , giving equal importance to the two channels. The use of the dilated LMI conditions can be carried out through a search procedure in the plane
, giving equal importance to the two channels. The use of the dilated LMI conditions can be carried out through a search procedure in the plane  . Figure 1 is a three-dimensional plot which depicts the waveform of
. Figure 1 is a three-dimensional plot which depicts the waveform of  in that plane. This figure clearly shows that optimality is achieved close to the direction where
in that plane. This figure clearly shows that optimality is achieved close to the direction where  . In this example, it is found that the minimum value of
. In this example, it is found that the minimum value of  which guarantees recovery is
which guarantees recovery is  . The abridged search procedure along the line
. The abridged search procedure along the line  produced a near optimal global performance of
produced a near optimal global performance of  and
and  when
when  . Clearly, in this example,improvement is being made in the region below
. Clearly, in this example,improvement is being made in the region below  where recovery is not necessarily there. Table 1 lists the simulation results obtained with the sufficient standard LMI conditions of Theorem 3.1 and with the sufficient dilated LMI conditions of Theorem 3.2.
where recovery is not necessarily there. Table 1 lists the simulation results obtained with the sufficient standard LMI conditions of Theorem 3.1 and with the sufficient dilated LMI conditions of Theorem 3.2.
 representing the LMI produced full-order dynamic output feedback controller.
representing the LMI produced full-order dynamic output feedback controller.The advantage of using the dilated rather than the standard LMI conditions is quite visible with this example. Indeed, around a 30% improvement on  and a 25% improvement on
and a 25% improvement on  performance levels were possible. However, this improvement comes at the expense of almost tripling the number of decision variables involved in the proposed dilated LMI conditions (see Table 1).
performance levels were possible. However, this improvement comes at the expense of almost tripling the number of decision variables involved in the proposed dilated LMI conditions (see Table 1).
6. Conclusion
This paper has presented new dilated LMI conditions for the design of multiobjective full-order dynamic output controllers in continuous-time systems that are able to cope not only with stability analysis and  performance specifications, but also, with
performance specifications, but also, with  performance specifications as well. The paper developed new controller synthesis procedures which offer no particular advantage for precisely known monoobjective systems, but significantly reduce conservatism in the multi-objective control problem, as the main property of these new dilated LMI conditions, besides the fact thattheyallow a complete independence between the standard Lyapunov matrix and the controller parametersis that they alwaysencompass the standard ones.A numerical simulation is presented which supports these claims. The extension of these results to other control issues such as the robust controller, model predictive controller, and filter design problems is rather straightforward and yet very useful.
performance specifications as well. The paper developed new controller synthesis procedures which offer no particular advantage for precisely known monoobjective systems, but significantly reduce conservatism in the multi-objective control problem, as the main property of these new dilated LMI conditions, besides the fact thattheyallow a complete independence between the standard Lyapunov matrix and the controller parametersis that they alwaysencompass the standard ones.A numerical simulation is presented which supports these claims. The extension of these results to other control issues such as the robust controller, model predictive controller, and filter design problems is rather straightforward and yet very useful.
References
Boyd S, El Ghaoui L, Feron E, Balakrishnan V: Linear Matrix Inequalities in System and Control Theory, SIAM Studies in Applied Mathematics. Volume 15. SIAM, Philadelphia, Pa, USA; 1994:xii+193.
Nesterov Y, Nemirovskii A: Interior-Point Polynomial Algorithms in Convex Programming, SIAM Studies in Applied Mathematics. Volume 13. SIAM, Philadelphia, Pa, USA; 1994:x+405.
Skelton RE, Iwazaki T, Grigoriadis G: A Unified Approach to Linear Control Design, Taylor and Francis Series in Systems and Control. Taylor and Francis, London, UK; 1997.
Crusius CAR, Trofino A: Sufficient LMI conditions for output feedback control problems. IEEE Transactions on Automatic Control 1999, 44(5):1053–1057. 10.1109/9.763227
Lee KH, Lee JH, Kwon WH: Sufficient LMI conditions for output feedback stabilization of linear discrete-time systems. IEEE Transactions on Automatic Control 2006, 51(4):675–680. 10.1109/TAC.2006.872766
Apkarian P, Tuan HD, Bernussou J: Continuous-time analysis, eigenstructure assignment, and synthesis with enhanced linear matrix inequalities (LMI) characterizations. IEEE Transactions on Automatic Control 2001, 46(12):1941–1946. 10.1109/9.975496
Ebihara Y, Hagiwara T: New dilated LMI characterizations for continuous-time multiobjective controller synthesis. Automatica 2004, 40(11):2003–2009. 10.1016/j.automatica.2004.06.009
Scherer C, Gahinet P, Chilali M: Multiobjective output-feedback control via LMI optimization. IEEE Transactions on Automatic Control 1997, 42(7):896–911. 10.1109/9.599969
Dettori M, Scherer CW: New robust stability and performance conditions based on parameter dependent multipliers. Proceedings of the 36th IEEE Conference on Decision and Control (CDC '00), 2000 5: 4187–4192.
Ebihara Y, Hagiwara T: A dilated LMI approach to robust performance analysis of linear time-invariant uncertain systems. Automatica 2005, 41(11):1933–1941. 10.1016/j.automatica.2005.05.023
Feron E, Apkarian P, Gahinet P: Analysis and synthesis of robust control systems via parameter-dependent Lyapunov functions. IEEE Transactions on Automatic Control 1996, 41(7):1041–1046. 10.1109/9.508913
Gahinet P, Apkarian P, Chilali M: Affine parameter-dependent Lyapunov functions and real parametric uncertainty. IEEE Transactions on Automatic Control 1996, 41(3):436–442. 10.1109/9.486646
Geromel JC, de Oliveira MC, Hsu L: LMI characterization of structural and robust stability. Linear Algebra and Its Applications 1998, 285(1–3):69–80.
Duan Z, Zhang J, Zhang C, Mosca E: Robust and filtering for uncertain linear systems. Automatica 2006, 42(11):1919–1926. 10.1016/j.automatica.2006.06.004
Peaucelle D, Arzelier D, Bachelier O, Bernussou J: A new robust D-stability condition for real convex polytopic uncertainty. Systems & Control Letters 2000, 40(1):21–30. 10.1016/S0167-6911(99)00119-X
Shaked U: Improved LMI representations for the analysis and the design of continuous-time systems with polytopic type uncertainty. IEEE Transactions on Automatic Control 2001, 46(4):652–656. 10.1109/9.917671
Xie W: An equivalent LMI representation of bounded real lemma for continuous-time systems. Journal of Inequalities and Applications 2008, 2008:-8.
de Oliveira MC, Bernussou J, Geromel JC: A new discrete-time robust stability condition. Systems & Control Letters 1999, 37(4):261–265. 10.1016/S0167-6911(99)00035-3
de Oliveira MC, Geromel JC, Bernussou J: Extended and norm characterizations and controller parametrizations for discrete-time systems. International Journal of Control 2002, 75(9):666–679. 10.1080/00207170210140212
Farges C, Peaucelle D, Arzelier D, Daafouz J: Robust performance analysis and synthesis of linear polytopic discrete-time periodic systems via LMIs. Systems & Control Letters 2007, 56(2):159–166. 10.1016/j.sysconle.2006.08.006
Arzelier D, Henrion D, Peaucelle D: Robust D-stabilization of a polytope of matrices. International Journal of Control 2002, 75(10):744–752. 10.1080/00207170210141824
Bachelier O, Peaucelle D, Arzelier D, Bernussou J: A precise robust matrix root-clustering analysis with respect to polytopic uncertainty. Proceedings of the American Control Conference, July 2000, Chicago, Ill, USA 5: 3331–3335.
Bosche J, Bachelier O, Mehdi D: An approach for robust matrix root-clustering analysis in a union of regions. IMA Journal of Mathematical Control and Information 2005, 22(3):227–239. 10.1093/imamci/dni007
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zrida, J., Dabboussi, K. New Dilated LMI Characterization for the Multiobjective Full-Order Dynamic Output Feedback Synthesis Problem. J Inequal Appl 2010, 608374 (2010). https://doi.org/10.1155/2010/608374
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/608374
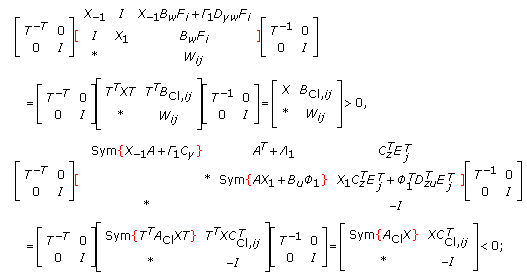
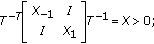


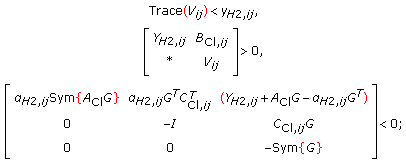
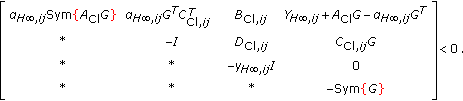

 in the plane
in the plane  .
.