- Research Article
- Open access
- Published:
Dynamics of a Predator-Prey System Concerning Biological and Chemical Controls
Journal of Inequalities and Applications volume 2010, Article number: 598495 (2010)
Abstract
We investigate an impulsive predator-prey system with Monod-Haldane type functional response and control strategies, especially, biological and chemical controls. Conditions for the stability of the prey-free positive periodic solution and for the permanence of the system are established via the Floquet theory and comparison theorem. Numerical examples are also illustrated to substantiate mathematical results and to show that the system could give birth to various kinds of dynamical behaviors including periodic doubling, and chaotic attractor. Finally, in discussion section, we consider the dynamic behaviors of the system when the growth rate of the prey varies according to seasonal effects.
1. Introduction
In recent years controlling insects and other arthropods has become an increasingly complex issue. There are many ways that can be used to help control the population of insect pests. Integrated Pest Management (IPM) is a pest control strategy that uses an array of complementary methods: natural predators and parasites, pest-resistant varieties, cultural practices, biological controls, various physical techniques, and the strategic use of pesticides.
Chemical control is one of simple methods for pest control. Pesticides are often useful because they quickly kill a significant portion of a pest population. However, there are many deleterious effects associated with the use of chemicals that need to be reduced or eliminated. These include human illness associated with pesticide applications, insect resistance to insecticides, contamination of soil and water, and diminution of biodiversity. As a result, it is required that we should combine pesticide efficacy tests with other ways of control. Another important way to control pest populations is biological control. It is defined as the reduction of pest populations by natural enemies and typically involves an active human role. Natural enemies of insect pests, also known as biological control agents, include predators, parasites, and pathogens. Virtually all pests have some natural enemies, and the key to successful pest control is to identify the pest and its natural enemies and release them at fixed times for pest control. Biological control can be an important component of Integrated Pest Management (IPM) programs. Such different pest control tactics should work together rather than against each other to accomplish an IPM program successfully [1, 2].
On the other hand, the relationship between pest and natural enemy can be expressed a predator(natural enemy)-prey(pest) system mathematically as follows:

where  and
and  represent the population density of the prey and the predator at time
represent the population density of the prey and the predator at time  , respectively. Usually,
, respectively. Usually,  is called the carrying capacity of the prey. The constant
is called the carrying capacity of the prey. The constant  is called intrinsic growth rate of the prey. The constants
is called intrinsic growth rate of the prey. The constants  ,
,  are the conversion rate and the death rate of the predator, respectively. The function
are the conversion rate and the death rate of the predator, respectively. The function  is the functional response of the predator which means prey eaten per predator per unit of time. Many scholars have studied such predator-prey systems with functional response, such as Holling-type [3–5], Beddington-type [6–9], and Ivlev-type [10–12]. One of well-known function response is of Monod-Haldane type [4, 5, 13]. The predator-prey system with Monod-Haldane type is described by the following differential equation:
is the functional response of the predator which means prey eaten per predator per unit of time. Many scholars have studied such predator-prey systems with functional response, such as Holling-type [3–5], Beddington-type [6–9], and Ivlev-type [10–12]. One of well-known function response is of Monod-Haldane type [4, 5, 13]. The predator-prey system with Monod-Haldane type is described by the following differential equation:

Therefore, to accomplish the aims discussed above, we need to consider impulsive differential equation as follows:

where the parameters  and
and  are the periods of the impulsive immigration or stock of the predator,
are the periods of the impulsive immigration or stock of the predator,  present the fraction of the prey which dies due to the harvesting or pesticides and so forth, and
present the fraction of the prey which dies due to the harvesting or pesticides and so forth, and  is the size of immigration or stock of the predator.
is the size of immigration or stock of the predator.
In fact, impulsive control methods can be found in almost every field of applied sciences. The theoretical investigation and its application analysis can be found in Bainov and Simeonov [14], Lakshmikantham et al. [15]. Moreover, the impulsive differential equations dealing with biological population dynamics are literate in [16–21]. In particular, Zhang et al. [20] studied the system (1.3) without chemical control. That is,  . They investigated the abundance of complex dynamics of the system (1.3) theoretically and numerically.
. They investigated the abundance of complex dynamics of the system (1.3) theoretically and numerically.
The main purpose of this paper is to investigate the dynamics of the system (1.3). In Section 3, we study qualitative properties of the system (1.3). In fact, we show the local stability of the prey-free periodic solution under some conditions and give a sufficient condition for the permanence of the system (1.3) by applying the Floquet theory. In Section 4 we numerically investigate the system (1.3) to figure out the influences of impulsive perturbations on inherent oscillation. Finally, in Section 5, we consider the dynamic behaviors of the system when the growth rate of the prey varies according to seasonal effects.
2. Basic Definitions and Lemmas
Before stating our main results, firstly, we give some notations, definitions and lemmas which will be useful for our main results.
Let  ,
,  and
and  . Denote
. Denote  as the set of all of nonnegative integers and
as the set of all of nonnegative integers and  as the right hand of the system (1.3). Let
as the right hand of the system (1.3). Let  , then
, then  is said to be in a class
is said to be in a class  if
if
(1) is continuous in
is continuous in  and
and  ,
,

and  exists for each
exists for each  ;
;
(2) is locally Lipschitzian in
is locally Lipschitzian in  .
.
Definition 2.1.
Let  and
and  . The upper right derivative of
. The upper right derivative of  with respect to the impulsive differential system (1.3) is defined as
with respect to the impulsive differential system (1.3) is defined as

It is from [15] that the smoothness properties of  guarantee the global existence and uniqueness of solutions to the system (1.3).
guarantee the global existence and uniqueness of solutions to the system (1.3).
We will use a comparison inequality of impulsive differential equations. Suppose that  satisfies the following hypotheses:
satisfies the following hypotheses:
-
(H)
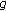
is continuous on
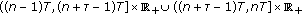 and the limits
and the limits 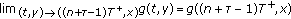 ,
, 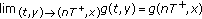 exist and are finite for
exist and are finite for 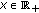 and
and 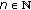 .
.
Lemma 2.2 (see [15]).
Suppose that  and
and

where  satisfies
satisfies  and
and  are nondecreasing for all
are nondecreasing for all  . Let
. Let  be the maximal solution for the impulsive Cauchy problem
be the maximal solution for the impulsive Cauchy problem

defined on  . Then
. Then  implies that
implies that  , where
, where  is any solution of (2.3).
is any solution of (2.3).
Similar result can be obtained when all conditions of the inequalities in the Lemma 2.2 are reversed. Note that if we have some smoothness conditions of  to guarantee the existence and uniqueness of the solutions for (2.4), then
to guarantee the existence and uniqueness of the solutions for (2.4), then  is exactly the unique solution of (2.4).
is exactly the unique solution of (2.4).
From Lemma 2.2, it is easily proven that the following lemma holds.
Lemma 2.3.
Let  be a solution of the system (1.3). Then one has the following:
be a solution of the system (1.3). Then one has the following:
(1)if  then
then  for all
for all  ;
;
(2)if  then
then  for all
for all  .
.
It follows from Lemma 2.3 that the positive quadrant  is an invariant region of the system (1.3).
is an invariant region of the system (1.3).
Even if the Floquet theory is well known, we would like to mention the theory to study the stability of the prey-free periodic solution as a solution of the system (1.3). For this, we present the Floquet theory for the linear  -periodic impulsive equation:
-periodic impulsive equation:

Then we introduce the following conditions.
()  and
and  , where
, where  is a set of all piecewise continuous matrix functions which is left continuous at
is a set of all piecewise continuous matrix functions which is left continuous at  , and
, and  is a set of all
is a set of all  matrices.
matrices.
()  ,
,  .
.
() There exists a  such that
such that  .
.
Let  be a fundamental matrix of (2.5), then there exists a unique nonsingular matrix
be a fundamental matrix of (2.5), then there exists a unique nonsingular matrix  such that
such that

By equality (2.6) there corresponds to the fundamental matrix  and the constant matrix
and the constant matrix  which we call the monodromy matrix of (2.5) (corresponding to the fundamental matrix of
which we call the monodromy matrix of (2.5) (corresponding to the fundamental matrix of  ). All monodromy matrices of (2.5) are similar and have the same eigenvalues. The eigenvalues
). All monodromy matrices of (2.5) are similar and have the same eigenvalues. The eigenvalues  of the monodromy matrices are called the Floquet multipliers of (2.5).
of the monodromy matrices are called the Floquet multipliers of (2.5).
Lemma 2.4 (Floquet theory [14]).
Let conditions (H1)–(H3) hold. Then the linear  -periodic impulsive equation (2.5) is
-periodic impulsive equation (2.5) is
(1)stale if and only if all multipliers  of (2.5) satisfy the inequality
of (2.5) satisfy the inequality  , and moreover, to those
, and moreover, to those  for which
for which  , there correspond simple elementary divisors;
, there correspond simple elementary divisors;
(2)asymptotically stable if and only if all multipliers  of (2.5) satisfy the inequality
of (2.5) satisfy the inequality  ;
;
(3)unstable if  for some
for some  .
.
3. Mathematical Analysis
In this section, we have focused on two main subjects, one is about the extinction of the prey and the other is about the coexistence of the prey and the predator. For the extinction, we have found out a condition that the population of the prey goes to zero as time goes by via the study of the stability of a prey-free periodic solution. For example, if the prey is regarded as a pest, it is important to figure out when the population of the prey dies out. For the reason, it is necessary to consider the stability of the prey-free periodic solution. On the other hand, for the coexistence, we have investigated that the populations of the prey and the predator become positive and finite under certain conditions.
3.1. Stability for a Prey-Free Periodic Solution
First of all, in order to study the extinction of the prey, the existence of a prey-free solution to the system (1.3) should be guaranteed. For the reason, we give some basic properties of the following impulsive differential equation which comes from the system (1.3) by setting 

The system (3.1) is a periodically forced linear system; it is easy to obtain from elementary calculations that


,  is a positive periodic solution of (3.1). Moreover, we can figure out that
is a positive periodic solution of (3.1). Moreover, we can figure out that

is the solution of (3.1). From (3.2) and (3.3), the following results can be easily obtained without the proof.
Lemma 3.1.
For every solution  and every positive periodic solution
and every positive periodic solution  of the system (3.1), it follows that
of the system (3.1), it follows that  tend to
tend to  as
as  . Thus, the complete expression for the prey-free periodic solution of the system (1.3) is obtained
. Thus, the complete expression for the prey-free periodic solution of the system (1.3) is obtained  .
.
Now, in the next theorem, the stability of the periodic solution  is investigated.
is investigated.
Theorem 3.2.
Let  be any solution of the system (1.3). Then the prey-free periodic solution
be any solution of the system (1.3). Then the prey-free periodic solution  is locally asymptotically stable if
is locally asymptotically stable if

Proof.
The local stability of the periodic solution  of the system (1.3) may be determined by considering the behavior of small amplitude perturbations of the solution. Define
of the system (1.3) may be determined by considering the behavior of small amplitude perturbations of the solution. Define  . Then they may be written as
. Then they may be written as

where  satisfies
satisfies

and  , the identity matrix. So the fundamental solution matrix is
, the identity matrix. So the fundamental solution matrix is

The resetting impulsive condition of the system (1.3) becomes

Note that all eigenvalues of

are  and
and  . Since
. Since

the condition  is equivalent to the equation
is equivalent to the equation

According to Lemma 2.4,  is locally stable.
is locally stable.
Remark 3.3.
-
(1)
It follows from Theorem 3.2 that the population of the prey could be controlled by using chemical or biological control parameters,
 ,
, 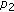 ,
, 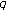 if the other parameters are fixed. (2) Figure 2 illustrates this phenomenon.
if the other parameters are fixed. (2) Figure 2 illustrates this phenomenon.
3.2. Permanence
It might be difficult to find out a necessary condition for the stability of the prey-free periodic solution  . Due to this fact, it is natural to have a question what a condition that makes all species coexist is. Before answering the question, first of all, we introduce a definition which keeps the concept of coexistence of the prey and the predator.
. Due to this fact, it is natural to have a question what a condition that makes all species coexist is. Before answering the question, first of all, we introduce a definition which keeps the concept of coexistence of the prey and the predator.
Definition 3.4.
The system (1.3) is permanent if there exists  such that, for any solution
such that, for any solution  of the system (1.3) with
of the system (1.3) with  ,
,

From a biological point of view, the populations of the prey and the predator in the system (1.3) cannot increase up to infinity due to restriction of resources. To show this phenomenon for the system (1.3) mathematically, we prove that all solutions to the system (1.3) are uniformly ultimately bounded in the next proposition.
Proposition 3.5.
There is an  such that
such that  for all
for all  large enough, where
large enough, where  is a solution of the system (1.3).
is a solution of the system (1.3).
Proof.
Let  be a solution of the system (1.3) and let
be a solution of the system (1.3) and let  . Then
. Then  , if
, if  and
and 

When  ,
,  and when
and when  ,
,  . Clearly, the right hand of (3.13), is bounded when
. Clearly, the right hand of (3.13), is bounded when  . So we can choose
. So we can choose  and
and  such that
such that

By Lemma 2.2, we can obtain that

for  . Therefore,
. Therefore,  is bounded by a constant for sufficiently large
is bounded by a constant for sufficiently large  . Hence there is an
. Hence there is an  such that
such that  for a solution
for a solution  with all
with all  large enough.
large enough.
Thanks to Proposition 3.5, we have only to prove the existence of a positive lower bound for the populations of the prey and the predator to justify the system is permanent.
Theorem 3.6.
The system (1.3) is permanent if

Proof.
Suppose  is any solution of the system (1.3) with
is any solution of the system (1.3) with  . From Proposition 3.5, we may assume that
. From Proposition 3.5, we may assume that  ,
,  ,
,  and
and  . Let
. Let 
 ,
,  . So, it is easily induced from Lemma 3.1 that
. So, it is easily induced from Lemma 3.1 that  for all
for all  large enough. Now we shall find an
large enough. Now we shall find an  such that
such that  for all
for all  large enough. We will do this in the following two steps.
large enough. We will do this in the following two steps.
Step 1.
Since

we can choose  ,
,  small enough such that
small enough such that  and
and 
 . Suppose that
. Suppose that  for all
for all  . Then we get
. Then we get  from above assumptions. By Lemma 2.2, we have
from above assumptions. By Lemma 2.2, we have  and
and  ,
,  , where
, where  is the solution of
is the solution of


Then there exists  such that
such that  for
for  . So we obtain that
. So we obtain that

for  . Let
. Let  and
and  . Integrating (3.20) on
. Integrating (3.20) on  ,
,  , we have
, we have 
 . Then we have
. Then we have  as
as  which is a contradiction. Hence there exists a
which is a contradiction. Hence there exists a  such that
such that  .
.
Step 2.
If  for all
for all  , then we are done. If not, we may let
, then we are done. If not, we may let  . Then
. Then  for
for  and, by the continuity of
and, by the continuity of  , we have
, we have  . In this step, we have only to consider two possible cases.
. In this step, we have only to consider two possible cases.
Case 1.

for some  . Then
. Then  . Select
. Select  such that
such that  and
and 
 , where
, where  . Let
. Let  . In this case we will show that there exists
. In this case we will show that there exists  such that
such that  . Otherwise, by (3.18) with
. Otherwise, by (3.18) with  , we have
, we have

and  . So we get
. So we get  and
and  for
for  . Also we get to know that
. Also we get to know that

for  . As in Step 1, we have
. As in Step 1, we have

Since  , we have
, we have

for  . Integrating (3.24) on
. Integrating (3.24) on  we have
we have

Thus  which is a contradiction. Now, let
which is a contradiction. Now, let  =
=  . Then
. Then  for
for  and
and  . So, we have, for
. So, we have, for  ,
,  .
.
Case 2.

, . Suppose that
. Suppose that  ,
,  . There are two possible cases for
. There are two possible cases for  .If
.If  for all
for all  , similar to (Case 1), we can prove there must be a
, similar to (Case 1), we can prove there must be a  such that
such that  . Here we omit it. Let
. Here we omit it. Let  . Then
. Then  for
for  and
and  . For
. For  , we have
, we have  . So,
. So,  and
and  for
for  . If there exists a
. If there exists a  such that
such that  . Let
. Let  . Then
. Then  for
for  and
and  . For
. For  , we have
, we have  .
.
Thus in both case the similar argument can be continued since  for some
for some  . This completes the proof.
. This completes the proof.
Remark 3.7.
4. Numerical Analysis on Impulsive Perturbations
It is well known that the continuous system (1.3) cannot be solved explicitly. Thus we should study the system (1.3) by using numerical method and research the long-term behavior of the solutions to get more information about the dynamic behaviors of the system (1.3). We thus numerically investigate the influence of impulsive perturbation. For this, we fix the parameters except the control parameters  ,
,  and
and  as follows:
as follows:

It is from [5] that the system (1.3) with  and
and  has an unique limit cycle. Moreover, Figure 1 shows that the phase portrait of the system (1.3) with
has an unique limit cycle. Moreover, Figure 1 shows that the phase portrait of the system (1.3) with  ,
,  , and
, and  has a limit cycle too. From Theorem 3.2, we know that the prey-free periodic solution
has a limit cycle too. From Theorem 3.2, we know that the prey-free periodic solution  is locally asymptotically stable provided that
is locally asymptotically stable provided that  . A typical prey-free periodic solution
. A typical prey-free periodic solution  of the system (1.3) is shown in Figure 2, where we observe how the variable
of the system (1.3) is shown in Figure 2, where we observe how the variable  oscillates in a stable cycle while the prey
oscillates in a stable cycle while the prey  rapidly decreases to zero. On the other hand, if the amount
rapidly decreases to zero. On the other hand, if the amount  of releasing species is smaller than
of releasing species is smaller than  , then the prey and the predator can coexist on a stable positive periodic solution (see Figure 1) and the system (1.3) can be permanent, which follows from Theorem 3.6.
, then the prey and the predator can coexist on a stable positive periodic solution (see Figure 1) and the system (1.3) can be permanent, which follows from Theorem 3.6.
Now we investigate the effect of impulsive perturbations. In Figure 3, we displayed bifurcation diagrams for the prey and predator populations as  increasing from 0 to 13 with an initial value
increasing from 0 to 13 with an initial value  . The resulting bifurcation diagram clearly show that the system (1.3) has rich dynamics including cycles, periodic doubling bifurcation, chaotic bands, periodic window, and period-halving bifurcation. Figures 4 and 5 are the magnified parts of Figure 3, and the windows of periodic behaviors are more visible.
. The resulting bifurcation diagram clearly show that the system (1.3) has rich dynamics including cycles, periodic doubling bifurcation, chaotic bands, periodic window, and period-halving bifurcation. Figures 4 and 5 are the magnified parts of Figure 3, and the windows of periodic behaviors are more visible.
As is evident from Figure 3, the solutions of the system (1.3) are  -periodic when
-periodic when  and
and  and
and  -periodic when
-periodic when  . Generally, periodic doubling leads to chaos. We can take a local view of this phenomenon in Figure 4. But Figures 4 and 6 show the route to chaos through the cascade of period four. This phenomenon is caused by sudden changes when
. Generally, periodic doubling leads to chaos. We can take a local view of this phenomenon in Figure 4. But Figures 4 and 6 show the route to chaos through the cascade of period four. This phenomenon is caused by sudden changes when  . We can also find such phenomena when
. We can also find such phenomena when  , and so on. One of interesting things is that they can lead to non-unique attractors. In fact, Figure 7 exhibits the existence of multiattractors when
, and so on. One of interesting things is that they can lead to non-unique attractors. In fact, Figure 7 exhibits the existence of multiattractors when  . These results show that just one parameter could give rise to multiple attractors. Narrow periodic windows and wide periodic windows are intermittently scattered (see Figure 3). At the end of the chaotic region, there is a cascade of period-halving bifurcation from chaos to one cycle. (see Figures 5 and 8). Periodic halving is the flip bifurcation in the opposite direction.
. These results show that just one parameter could give rise to multiple attractors. Narrow periodic windows and wide periodic windows are intermittently scattered (see Figure 3). At the end of the chaotic region, there is a cascade of period-halving bifurcation from chaos to one cycle. (see Figures 5 and 8). Periodic halving is the flip bifurcation in the opposite direction.
5. Discussion
In this paper, we have studied the effects of control strategies on a predator-prey system with Monod-Haldane type functional response. Conditions for the system to be extinct are given by using the Floquet theory of impulsive differential equation and small amplitude perturbation skills. Also, it is proved that the system the system (1.3) is permanent via the comparison theorem. Moreover, numerical examples on impulsive perturbations have been illustrated to substantiate our mathematical results and to show that the system we have considered in this paper gives birth to various kinds of dynamical behaviors.
Actually, in the real world, there are a number of environmental factors we should consider to describe the world more realistically. Among them, seasonal effect on the prey is one of the most important factors in the ecological systems. There are many ways to apply such phenomena in an ecological system [22, 23]. In this context, we think about the intrinsic growth rate  in the system (1.3) as periodically varying function of time due to seasonal variation, which is superimposed as follows:
in the system (1.3) as periodically varying function of time due to seasonal variation, which is superimposed as follows:

where the parameter  represents the degree of seasonality,
represents the degree of seasonality,  is the magnitude of the perturbation in
is the magnitude of the perturbation in  and
and  is the angular frequency of the fluctuation caused by seasonality. Now, the system (1.3) can be changed as follows:
is the angular frequency of the fluctuation caused by seasonality. Now, the system (1.3) can be changed as follows:

And then we get the following results via similar methods used in the previous sections.
Theorem 5.1.
Let  be any solution of the system (5.2). Then the prey-free periodic solution
be any solution of the system (5.2). Then the prey-free periodic solution  is locally asymptotically stable if
is locally asymptotically stable if

Proposition 5.2.
There is an  such that
such that  for all
for all  large enough, where
large enough, where  is a solution of the system (5.2).
is a solution of the system (5.2).
Theorem 5.3.
The system (5.2) is permanent if

Thus, the seasonal effect on the prey may have also deeply influences on dynamics of the system (1.3).
References
Lu Z, Chi X, Chen L: Impulsive control strategies in biological control of pesticide. Theoretical Population Biology 2003, 64(1):39–47. 10.1016/S0040-5809(03)00048-0
Tang S, Xiao Y, Chen L, Cheke RA: Integrated pest management models and their dynamical behaviour. Bulletin of Mathematical Biology 2005, 67(1):115–135. 10.1016/j.bulm.2004.06.005
Holling CS: The functional response of predator to prey density and its role in mimicry and population regulations. Memoirs of the Entomological Society of Canada 1965, 45: 1–60.
Hsu SB, Huang TW: Global stability for a class of predator-prey systems. SIAM Journal on Applied Mathematics 1995, 55(3):763–783. 10.1137/S0036139993253201
Ruan S, Xiao D: Global analysis in a predator-prey system with nonmonotonic functional response. SIAM Journal on Applied Mathematics 2001, 61(4):1445–1472. 10.1137/S0036139999361896
Baek HK: Qualitative analysis of Beddington-DeAngelis type impulsive predator-prey models. Nonlinear Analysis: Real World Applications 2010, 11(3):1312–1322. 10.1016/j.nonrwa.2009.02.021
Beddington JR: Mutual interference between parasites or predator and its effect on searching efficiency. Journal of Animal Ecology 1975, 44: 331–340. 10.2307/3866
Fan M, Kuang Y: Dynamics of a nonautonomous predator-prey system with the Beddington-DeAngelis functional response. Journal of Mathematical Analysis and Applications 2004, 295(1):15–39. 10.1016/j.jmaa.2004.02.038
Hwang T-W: Uniqueness of limit cycles of the predator-prey system with Beddington-DeAngelis functional response. Journal of Mathematical Analysis and Applications 2004, 290(1):113–122. 10.1016/j.jmaa.2003.09.073
Feng J-W, Chen S-H: Global asymptotic behavior for the competing predators of the Ivlev types. Mathematica Applicata 2000, 13(4):85–88.
Ivlev VS: Experimental Ecology of the Feeding of Fishes. Yale University Press; 1961.
Sugie J: Two-parameter bifurcation in a predator-prey system of Ivlev type. Journal of Mathematical Analysis and Applications 1998, 217(2):349–371. 10.1006/jmaa.1997.5700
Sokol W, Howell JA: Kineties of phenol oxidation by ashed cell. Biotechnology and Bioengineering 1980, 23: 2039–2049.
Bainov DD, Simeonov PS: Impulsive Differential Equations:Periodic Solutions and Applications, Pitman Monographs and Surveys in Pure and Applied Mathematics. Volume 66. Longman Science & Technical, Harlo, UK; 1993.
Lakshmikantham V, Baĭnov DD, Simeonov PS: Theory of Impulsive Differential Equations, Series in Modern Applied Mathematics. Volume 6. World Scientific, Teaneck, NJ, USA; 1989:xii+273.
Li Z, Wang W, Wang H: The dynamics of a Beddington-type system with impulsive control strategy. Chaos, Solitons & Fractals 2006, 29(5):1229–1239. 10.1016/j.chaos.2005.08.195
Liu B, Zhang Y, Chen L: Dynamic complexities in a Lotka-Volterra predator-prey model concerning impulsive control strategy. International Journal of Bifurcation and Chaos 2005, 15(2):517–531. 10.1142/S0218127405012338
Wang H, Wang W: The dynamical complexity of a Ivlev-type prey-predator system with impulsive effect. Chaos, Solitons & Fractals 2008, 38(4):1168–1176. 10.1016/j.chaos.2007.02.008
Wang W, Wang H, Li Z: The dynamic complexity of a three-species Beddington-type food chain with impulsive control strategy. Chaos, Solitons & Fractals 2007, 32(5):1772–1785. 10.1016/j.chaos.2005.12.025
Zhang S, Tan D, Chen L: Chaos in periodically forced Holling type IV predator-prey system with impulsive perturbations. Chaos, Solitons & Fractals 2006, 27(4):980–990. 10.1016/j.chaos.2005.04.065
Zhang S, Dong L, Chen L: The study of predator-prey system with defensive ability of prey and impulsive perturbations on the predator. Chaos, Solitons & Fractals 2005, 23(2):631–643. 10.1016/j.chaos.2004.05.044
Cushing JM: Periodic time-dependent predator-prey systems. SIAM Journal on Applied Mathematics 1977, 32(1):82–95. 10.1137/0132006
Gakkhar S, Naji RK: Chaos in seasonally perturbed ratio-dependent prey-predator system. Chaos, Solitons & Fractals 2003, 15(1):107–118. 10.1016/S0960-0779(02)00114-5
Acknowledgments
The first author is supported by Catholic University of Daegu Research Grant. The second author was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (2010-0004426).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kim, H., Baek, H. Dynamics of a Predator-Prey System Concerning Biological and Chemical Controls. J Inequal Appl 2010, 598495 (2010). https://doi.org/10.1155/2010/598495
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/598495
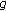
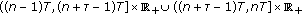 and the limits
and the limits 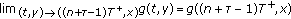 ,
, 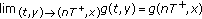 exist and are finite for
exist and are finite for 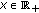 and
and 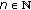 .
. ,
, 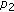 ,
, 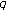 if the other parameters are fixed. (2) Figure
if the other parameters are fixed. (2) Figure  in the system (1.3).
in the system (1.3).
 -period solution of (1. 3) for
-period solution of (1. 3) for  .
.
 . (a)
. (a)  is plotted. (b)
is plotted. (b)  is plotted.
is plotted.
 ranging from
ranging from  . (a)
. (a)  is plotted. (b)
is plotted. (b)  is plotted.
is plotted.
 ranging from
ranging from  . (a)
. (a)  is plotted. (b)
is plotted. (b)  is plotted.
is plotted.
 ranging from
ranging from  . (a)
. (a)  is plotted. (b)
is plotted. (b)  is plotted.
is plotted.
 . (b)
. (b)  . (c)
. (c)  . (d)
. (d)  .
.
 . (a) Solution with initial values
. (a) Solution with initial values  . (b) Solution with initial values
. (b) Solution with initial values  .
.
 -periodic solutions to cycles of (1. 3). (a) Phase portrait of a
-periodic solutions to cycles of (1. 3). (a) Phase portrait of a  -period solution for
-period solution for  . (b) Phase portrait of a
. (b) Phase portrait of a  -period solution for
-period solution for  . (c) Phase portrait of a
. (c) Phase portrait of a  -period solution for
-period solution for  .
.