- Research Article
- Open access
- Published:
First-Order Twistor Lifts
Journal of Inequalities and Applications volume 2010, Article number: 594843 (2010)
Abstract
The use of twistor methods in the study of Jacobi fields has proved quite fruitful, leading to a series of results. L. Lemaire and J. C. Wood proved several properties of Jacobi fields along harmonic maps from the two-sphere to the complex projective plane and to the three- and four-dimensional spheres, by carefully relating the infinitesimal deformations of the harmonic maps to those of the holomorphic data describing them. In order to advance this programme, we prove a series of relations between infinitesimal properties of the map and those of its twistor lift. Namely, we prove that isotropy and harmonicity to first order of the map correspond to holomorphicity to first order of its lift into the twistor space, relatively to the standard almost complex structures  and
and  . This is done by obtaining first-order analogues of classical twistorial constructions.
. This is done by obtaining first-order analogues of classical twistorial constructions.
1. Introduction
Harmonic maps are mappings  between Riemannian manifolds
between Riemannian manifolds  and
and  which extremize the energy functional
which extremize the energy functional

Letting  denote the tangent bundle of
denote the tangent bundle of  , one can (locally) characterize harmonic maps as solutions of the nonlinear second-order differential equation
, one can (locally) characterize harmonic maps as solutions of the nonlinear second-order differential equation

where  denotes the tension field of
denotes the tension field of  ,
,

A bibliography can be found in [1] and for some useful summaries on this topic, see [2, 3].
The infinitesimal deformations of a harmonic map are called Jacobi fields. More precisely, let  be a smooth map and denote by
be a smooth map and denote by  the set of smooth sections of the pull-back bundle
the set of smooth sections of the pull-back bundle  . If
. If  is harmonic and
is harmonic and  is a vector field along it,
is a vector field along it,  is said to be a Jacobi field (along
is said to be a Jacobi field (along  ) if it satisfies the linear Jacobi equation
) if it satisfies the linear Jacobi equation , where the Jacobi operator
, where the Jacobi operator is defined by
is defined by

Here,  is the Laplacian on
is the Laplacian on  ,
,

and, letting  denote the curvature tensor of
denote the curvature tensor of  ,
,

Jacobi fields are characterized as lying in the kernel of the second variation of the energy functional. Indeed, if  is a two-parameter variation of a harmonic map
is a two-parameter variation of a harmonic map  , then, writing
, then, writing  and
and  , the Hessian
, the Hessian of
of  is the bilinear operator on
is the bilinear operator on  given by
given by

so that a Jacobi field  (along
(along  ) is characterized by the condition
) is characterized by the condition

A Jacobi field is called integrable if it is tangent to a deformation through harmonic maps. In [4, 5], the question of whether all Jacobi fields are integrable is answered for the case where the domain is the two-sphere and the codomain the two-dimensional complex projective space or the three- and four-dimensional sphere. This was done by relating the deformations of the map associated with the Jacobi field and those of the twistor lift of the map. More precisely, given an oriented even-dimensional manifold  , we can construct its (positive) twistor space
, we can construct its (positive) twistor space  . This manifold admits two natural almost complex structures
. This manifold admits two natural almost complex structures  and
and  . Given a map
. Given a map  from a Riemann surface
from a Riemann surface  , harmonicity is intimately related with the existence of a
, harmonicity is intimately related with the existence of a  -holomorphic lift
-holomorphic lift  , whereas isotropy is related with the existence of a
, whereas isotropy is related with the existence of a  -holomorphic lift
-holomorphic lift  (see [6]). On the other hand, Jacobi vector fields induce families of maps which are harmonic to first-order and, in some cases, isotropic to first order. The translation of these first order properties in terms of twistor lifts plays an important role on the study of the Jacobi fields and we shall exhibit how this translation can be established in general.
(see [6]). On the other hand, Jacobi vector fields induce families of maps which are harmonic to first-order and, in some cases, isotropic to first order. The translation of these first order properties in terms of twistor lifts plays an important role on the study of the Jacobi fields and we shall exhibit how this translation can be established in general.
This work is divided as follows: in the next two sections, we recall some well-known results concerning twistor lifts of harmonic and isotropic maps. In Section 4, we show how this constructions generalize to their parametric versions and examine more closely the construction when the codomain is a four-dimensional manifold. We leave to the last section some technical proofs.
2. The Setup
2.1. Twistor Spaces
Let  be an oriented even-dimensional Euclidean space, equipped with a metric
be an oriented even-dimensional Euclidean space, equipped with a metric  . A Hermitian structure
. A Hermitian structure on
on  is
is  with
with  and
and  for all
for all  . We say that
. We say that  is positive if there is a positive basis of
is positive if there is a positive basis of  of the form
of the form  and negative otherwise. The set of all positive Hermitian structures (resp., all negative Hermitian structures) on
and negative otherwise. The set of all positive Hermitian structures (resp., all negative Hermitian structures) on  is denoted by
is denoted by  (resp.,
(resp.,  ). The Lie group
). The Lie group  acts transitively on
acts transitively on  by the formula
by the formula  and the isotropy subgroup at
and the isotropy subgroup at  is given by
is given by

Letting  and
and  , we easily conclude that
, we easily conclude that

In particular, the tangent space of  at
at  is given by
is given by  . In this vector space, we can introduce a complex structure
. In this vector space, we can introduce a complex structure  defining
defining

When equipped with  , the manifold
, the manifold  is a complex manifold.
is a complex manifold.
Given  with a Hermitian structure
with a Hermitian structure  , we can consider on
, we can consider on  its
its  and
and  -parts given as usual by
-parts given as usual by

These are isotropic subspaces, in the sense that  for all
for all  in
in  (or in
(or in  ). Associating an Hermitian structure
). Associating an Hermitian structure  on
on  with its
with its  -space
-space  gives a 1–1 correspondence between Hermitian structures and maximal isotropic subspaces. We say that a maximal isotropic subspace is positive if the corresponding orthogonal complex structure is positive and we denote the set of all such subspaces by
gives a 1–1 correspondence between Hermitian structures and maximal isotropic subspaces. We say that a maximal isotropic subspace is positive if the corresponding orthogonal complex structure is positive and we denote the set of all such subspaces by  .
.
Let  be an oriented even-dimensional vector bundle over a manifold
be an oriented even-dimensional vector bundle over a manifold  equipped with a connection
equipped with a connection  and a parallel metric
and a parallel metric  . Then, we may take the bundle
. Then, we may take the bundle

whose fibre at  is precisely
is precisely  . If
. If  is Riemann surface, the vector bundle
is Riemann surface, the vector bundle  has vanishing
has vanishing  -part of its curvature tensor and therefore admits a unique structure as a holomorphic bundle over
-part of its curvature tensor and therefore admits a unique structure as a holomorphic bundle over  , by a well-known theorem of Koszul and Malgrange [7]. This induces a holomorphic structure
, by a well-known theorem of Koszul and Malgrange [7]. This induces a holomorphic structure  on the bundle
on the bundle  for which a section
for which a section  of
of  is holomorphic if and only if [6] (see [8]).
is holomorphic if and only if [6] (see [8]).

Let  be an oriented Riemannian manifold with dimension
be an oriented Riemannian manifold with dimension  . We call (positive) twistor space of
. We call (positive) twistor space of  the bundle whose fibre at
the bundle whose fibre at  is precisely
is precisely  ; that is,
; that is,

The Riemannian connection on  induces a splitting of the tangent space to
induces a splitting of the tangent space to  into vertical and horizontal parts,
into vertical and horizontal parts,  . Namely, if
. Namely, if  denotes the canonical projection defined by
denotes the canonical projection defined by  , then
, then

With respect to this decomposition,  maps
maps  isomorphically into
isomorphically into  and allows to define an almost complex structure
and allows to define an almost complex structure  on
on  as the pull-back of
as the pull-back of  on
on  . Together with (2.3), this allows to define two almost complex structures
. Together with (2.3), this allows to define two almost complex structures  and
and  on
on  by the formulae
by the formulae

When equipped with  ,
,  is never a complex manifold; as for
is never a complex manifold; as for  , it is integrable if and only if
, it is integrable if and only if  is conformally flat (
is conformally flat ( ) or anti-self-dual (
) or anti-self-dual ( ) (for more details, see [6, 9, 10]; a discussion on this topic can also be found in [11] and references therein).
) (for more details, see [6, 9, 10]; a discussion on this topic can also be found in [11] and references therein).
Notice that  is a holomorphic map for any of these complex structures; that is, for
is a holomorphic map for any of these complex structures; that is, for  or
or  , one has that
, one has that

Definition 2.1.
Let  and
and  be two almost complex manifolds. Let
be two almost complex manifolds. Let  be a decomposition of
be a decomposition of  into
into  -stable subbundles; that is,
-stable subbundles; that is,  and
and  . We shall call such a decomposition a
. We shall call such a decomposition a  -stable decomposition. Let
-stable decomposition. Let  be a smooth map. We shall say that
be a smooth map. We shall say that  is
is  -holomorphic if
-holomorphic if

Analogously we define  -holomorphic maps.
-holomorphic maps.
A smooth map  is holomorphic if and only if it is both
is holomorphic if and only if it is both  and
and  -holomorphic for some, and so any, stable decomposition
-holomorphic for some, and so any, stable decomposition  . Taking
. Taking  , the decomposition
, the decomposition  is clearly stable for both the almost complex structures
is clearly stable for both the almost complex structures  and
and  on
on  .
.
Remark 2.2.
We can easily introduce a metric on the twistor space  : let
: let  and consider the tangent space at this point,
and consider the tangent space at this point,  . We know that we have the identifications
. We know that we have the identifications  and
and  . To get a metric on
. To get a metric on  , transport the metric from that on
, transport the metric from that on  ; that is,
; that is,  , for all
, for all  ,
, , where
, where  denotes the metric on
denotes the metric on  at
at  . For the vertical space
. For the vertical space  , we can consider the restriction of the metric on the space
, we can consider the restriction of the metric on the space  . Finally, we declare
. Finally, we declare  and
and  to be orthogonal under the metric
to be orthogonal under the metric  ; that is,
; that is,  , for all
, for all  ,
,  . With this metric, the decomposition
. With this metric, the decomposition  is orthogonal and
is orthogonal and  -stable (
-stable ( ),
),  (
( ) are almost Hermitian manifolds and the projection map
) are almost Hermitian manifolds and the projection map  is a Riemannian submersion.
is a Riemannian submersion.
2.2. Conformal and Isotropic Maps
Given a smooth map  ,
,  is said to be weakly conformal at
is said to be weakly conformal at  if there is
if there is  with
with

If  , then
, then  is said to be a regular point (of
is said to be a regular point (of  ) and the map
) and the map  is called conformal at
is called conformal at  . Moreover, a map which is conformal (resp., weakly conformal) at all points
. Moreover, a map which is conformal (resp., weakly conformal) at all points  is said to be a conformal map (resp., a weakly conformal map).
is said to be a conformal map (resp., a weakly conformal map).
If  is an almost Hermitian manifold, any holomorphic (resp., antiholomorphic) map
is an almost Hermitian manifold, any holomorphic (resp., antiholomorphic) map  is (weakly) conformal as it maps
is (weakly) conformal as it maps  to
to  (resp., to
(resp., to  ). A stronger property than conformality is isotropy: if
). A stronger property than conformality is isotropy: if  is a smooth map from a Riemann surface,
is a smooth map from a Riemann surface,  is isotropic if [12]
is isotropic if [12]

where  . Actually, the condition (2.13) can be weakened to
. Actually, the condition (2.13) can be weakened to

To check this, establish an induction on  : if
: if  the result is trivial. Assuming now that (2.14) implies (2.13) for all
the result is trivial. Assuming now that (2.14) implies (2.13) for all  and taking
and taking  with
with  , we may assume without loss of generality that
, we may assume without loss of generality that  ,
,  and we get
and we get

Since  and
and  , both terms in the above expression vanish.
, both terms in the above expression vanish.
Moreover, letting  in (2.13), it is easy to check that an isotropic map from a Riemann surface is a (weakly) conformal map.
in (2.13), it is easy to check that an isotropic map from a Riemann surface is a (weakly) conformal map.
Let  be a smooth map from a Riemann surface
be a smooth map from a Riemann surface  . We shall say that
. We shall say that  is an umbilic point (of
is an umbilic point (of  ) if
) if  is a
is a  -linearly dependent set. If
-linearly dependent set. If  is such that all points
is such that all points  are umbilic, we shall say that
are umbilic, we shall say that  is totally umbilic (see [6]).
is totally umbilic (see [6]).
3. Nonparametric Twistorial Constructions
The following are well-known twistorial constructions [13] (see also [6]).
Theorem 3.1.
If  is holomorphic, the projection map
is holomorphic, the projection map  is isotropic. Conversely, if
is isotropic. Conversely, if  is a conformal totally umbilic immersion, there is (locally) a holomorphic map
is a conformal totally umbilic immersion, there is (locally) a holomorphic map  such that
such that  .
.
If  is holomorphic, the projection map
is holomorphic, the projection map  is harmonic. Conversely, if
is harmonic. Conversely, if  is a conformal harmonic map, there is (locally) a holomorphic map
is a conformal harmonic map, there is (locally) a holomorphic map  such that
such that  .
.
We shall sketch the proof of this result. We start by noticing that given a smooth map  obtained as the projection of
obtained as the projection of  ,
,  , without requiring further conditions à priori on
, without requiring further conditions à priori on  , nothing guarantees that
, nothing guarantees that  is holomorphic relatively to the induced almost Hermitian structure
is holomorphic relatively to the induced almost Hermitian structure  on
on  ; if it is, we shall say that the structure
; if it is, we shall say that the structure  is strictly compatible with
is strictly compatible with  (or that the map
(or that the map  is a strictly compatible twistor lift of
is a strictly compatible twistor lift of  ). Such a structure
). Such a structure  can exist if and only if
can exist if and only if  is isotropic: in other words, if and only if
is isotropic: in other words, if and only if  is (weakly) conformal. If
is (weakly) conformal. If  preserves
preserves  but does not necessarily render
but does not necessarily render  holomorphic, we shall say that
holomorphic, we shall say that  (or the map
(or the map  ) is compatible with
) is compatible with  .
.
If  is given as the projection
is given as the projection  of an
of an  -holomorphic map
-holomorphic map  (
( or
or  ), then
), then  is holomorphic with respect to the induced almost Hermitian structure
is holomorphic with respect to the induced almost Hermitian structure  on
on  :
:

In particular,  is (weakly) conformal. Moreover, the above equivalence shows that any strictly compatible lift of
is (weakly) conformal. Moreover, the above equivalence shows that any strictly compatible lift of  is
is  -holomorphic. On the opposite direction, let
-holomorphic. On the opposite direction, let  be a conformal map. Let
be a conformal map. Let  denote the normal bundle of
denote the normal bundle of  in
in  . We may decompose the connection on
. We may decompose the connection on  into its tangent and normal parts,
into its tangent and normal parts,  . Hence, on
. Hence, on  we have a metric
we have a metric  and connection
and connection  inherited from those on
inherited from those on  . Moreover, we may take the bundle
. Moreover, we may take the bundle  over
over  which has the
which has the  -holomorphic structure. Since
-holomorphic structure. Since  is conformal, we may transfer the Hermitian structure
is conformal, we may transfer the Hermitian structure  of
of  into
into  . Hence, we have a natural map
. Hence, we have a natural map

Taking any holomorphic section of  and composing with
and composing with  , we obtain a strictly compatible twistor lift
, we obtain a strictly compatible twistor lift  of
of  . Since any such lift is
. Since any such lift is  -holomorphic, we have just proved the following result.
-holomorphic, we have just proved the following result.
Proposition 3.2.
Given  ,
,  is conformal if and only if
is conformal if and only if  is (locally) the projection of an
is (locally) the projection of an  -holomorphic map
-holomorphic map  .
.
To proceed, we need the following result [13].
Proposition 3.3.
Let  and let
and let  . Take
. Take  the section of
the section of  corresponding to
corresponding to  . Then, the map
. Then, the map  is
is  -holomorphic if and only if
-holomorphic if and only if  is holomorphic with respect to
is holomorphic with respect to  and
and

The map  is
is  -holomorphic if and only if
-holomorphic if and only if  is holomorphic with respect to
is holomorphic with respect to  and
and

Let  be a
be a  -holomorphic map and let
-holomorphic map and let  be the corresponding section of
be the corresponding section of  . If
. If  is the projection map, we have that
is the projection map, we have that  is
is  -holomorphic. In particular,
-holomorphic. In particular,  . Since
. Since  is
is  -holomorphic, we can write
-holomorphic, we can write

and, inductively, it follows that  for all
for all  so that
so that  is isotropic. Conversely, let
is isotropic. Conversely, let  be a conformal totally umbilic map. In this case, we consider the manifold
be a conformal totally umbilic map. In this case, we consider the manifold  equipped with the opposite holomorphic structure-
equipped with the opposite holomorphic structure- and again construct the holomorphic bundle
and again construct the holomorphic bundle  . For this structure, a section
. For this structure, a section  is holomorphic if and only if
is holomorphic if and only if  . Since
. Since  is conformal, we may define the map
is conformal, we may define the map  as in (3.2). On the other hand, because
as in (3.2). On the other hand, because  is totally umbilic, we know that
is totally umbilic, we know that  lies in the span of
lies in the span of  ; in other words, if
; in other words, if  is any almost Hermitian structure on
is any almost Hermitian structure on  strictly compatible with
strictly compatible with  ,
,  lies in
lies in  . We may therefore conclude that
. We may therefore conclude that  is
is  -holomorphic. As a matter of fact, given a holomorphic section
-holomorphic. As a matter of fact, given a holomorphic section  of
of  and considering
and considering  , we have that
, we have that  . We may write
. We may write

since  and
and  lie in
lie in  . In particular,
. In particular, and so
and so

and therefore we conclude that  is
is  -holomorphic.
-holomorphic.
With a similar argument, let  be a
be a  -holomorphic map and let
-holomorphic map and let  be the section of
be the section of  corresponding to
corresponding to  . Then, taking the projection map
. Then, taking the projection map  , we get
, we get

Since  is
is  -holomorphic,
-holomorphic,  lies in
lies in  . From (iv) in Proposition 3.3, we conclude that
. From (iv) in Proposition 3.3, we conclude that  lies in
lies in  and therefore has vanishing
and therefore has vanishing  -part. From the reality of
-part. From the reality of  , we have that
, we have that  and so
and so  is harmonic. Conversely, if
is harmonic. Conversely, if  is conformal and harmonic, we may take the bundle
is conformal and harmonic, we may take the bundle  and the map
and the map  in (3.2). Since
in (3.2). Since  is harmonic,
is harmonic,  is holomorphic with respect to the
is holomorphic with respect to the  and
and  structures [6, 8]: letting
structures [6, 8]: letting  denote a holomorphic section of
denote a holomorphic section of  and
and  the composition
the composition  , then,
, then,  and
and

Since  is harmonic,
is harmonic,  . On the other hand, since
. On the other hand, since  is holomorphic,
is holomorphic,  . Finally,
. Finally,

shows that  and so that
and so that  is holomorphic. Therefore, taking any holomorphic section of
is holomorphic. Therefore, taking any holomorphic section of  and composing with
and composing with  give a
give a  -holomorphic lift of
-holomorphic lift of  .
.
Remark 3.4.
Notice that to guarantee the existence of the  -holomorphic lift for
-holomorphic lift for  , the important fact was that
, the important fact was that  belongs to the
belongs to the  -part of
-part of  for any almost Hermitian structure strictly compatible with
for any almost Hermitian structure strictly compatible with  . This is guaranteed if
. This is guaranteed if  is a totally umbilic map, but it is not strictly necessary. For instance, if
is a totally umbilic map, but it is not strictly necessary. For instance, if  is an isotropic map, the vectors
is an isotropic map, the vectors  ,
,  span an isotropic subspace. If this vectors are linearly independent, taking this space as the
span an isotropic subspace. If this vectors are linearly independent, taking this space as the  -space of
-space of  , then
, then  is a
is a  -holomorphic lift of
-holomorphic lift of  , although
, although  may be a map into
may be a map into  ; on the other hand, if
; on the other hand, if  is totally umbilic, then we may take
is totally umbilic, then we may take  either as the unique strictly compatible map into
either as the unique strictly compatible map into  or into
or into  and both these maps are
and both these maps are  -holomorphic.
-holomorphic.
4. First-Order Twistorial Constructions
4.1. Harmonicity and Isotropy to First Order
Let  denote an interval of the real line containing
denote an interval of the real line containing  . Given a (family of) map(s)
. Given a (family of) map(s)  ,
,  , we say that
, we say that  is harmonic to first order if
is harmonic to first order if

where  and
and  .
.
Let  be a harmonic map,
be a harmonic map,  a vector field along
a vector field along  , and
, and  a one-parameter variation of
a one-parameter variation of  . We say that
. We say that  is tangent to
is tangent to  if
if  . The following result is a key ingredient in what follows [4]:
. The following result is a key ingredient in what follows [4]:
Proposition 4.1.
Let  be a harmonic map between compact manifolds
be a harmonic map between compact manifolds  and
and  . Let
. Let  be a vector field along
be a vector field along  and
and  a one-parameter variation of
a one-parameter variation of  tangent to
tangent to  . Then,
. Then,

In particular,  is Jacobi if and only if any tangent one-parameter variation is harmonic to first order.
is Jacobi if and only if any tangent one-parameter variation is harmonic to first order.
We have seen in Theorem 3.1 that harmonicity was not enough to establish a relation with possible twistor lifts of a map conformality and was also a key ingredient, as maps obtained as projections of twistorial maps must be holomorphic with respect to some almost Hermitian structure along the map. On the other hand, when the domain is the  -sphere, harmonicity implies (weak) conformality or even isotropy, the last case occurring if the target manifold is itself also a sphere or the complex projective space [12, 14].
-sphere, harmonicity implies (weak) conformality or even isotropy, the last case occurring if the target manifold is itself also a sphere or the complex projective space [12, 14].
Let  be a Riemann surface and
be a Riemann surface and  a smooth map. The map
a smooth map. The map  is said to be conformal to first order if [15]
is said to be conformal to first order if [15]

Analogously,  is said to be isotropic to first order,
is said to be isotropic to first order,

As for the nonparametric case, one can prove [16] that condition (4.4) can be weakened to the following

As in the nonparametric case, harmonicity to first order implies conformality to first order for maps defined on the two-sphere and even isotropy when the codomain is itself a real or complex space form [15].
4.2. Twistorial Constructions
As we have seen, Jacobi fields induce variations that are harmonic (and, in some cases, conformal or even isotropic) to first order. On the other hand, in Section 2 we have seen that conformality, harmonicity, and isotropy of the map  correspond to
correspond to  ,
,  and
and  -holomorphicity of the twistor lift
-holomorphicity of the twistor lift  . As we shall see, these results do have a first-order version as follows. We start with a definition.
. As we shall see, these results do have a first-order version as follows. We start with a definition.
Definition 4.2.
Let  be an almost complex manifold and
be an almost complex manifold and  an almost Hermitian manifold. Given a smooth map
an almost Hermitian manifold. Given a smooth map  , we say that
, we say that  is holomorphic to first order if
is holomorphic to first order if  is holomorphic and
is holomorphic and

where  is the Levi-Civita connection on
is the Levi-Civita connection on  induced by the metric
induced by the metric  . Moreover, if
. Moreover, if  is a
is a  -stable decomposition of
-stable decomposition of  , orthogonal with respect to
, orthogonal with respect to  , we shall say that
, we shall say that  is
is  -holomorphic to first order if
-holomorphic to first order if  is
is  -holomorphic and
-holomorphic and

where  is the restriction of
is the restriction of  to
to  . Changing
. Changing  to
to  gives the definition of
gives the definition of  -holomorphicity to first order.
-holomorphicity to first order.
In contrast with the nonparametric case, it is not obvious that  -holomorphicity to first order implies
-holomorphicity to first order implies  -holomorphicity to first order. As a matter of fact, from (4.6), it only follows that
-holomorphicity to first order. As a matter of fact, from (4.6), it only follows that  . However, we do have the following.
. However, we do have the following.
Lemma 4.3.
Let  be a smooth map and let
be a smooth map and let  be a
be a  -stable decomposition of
-stable decomposition of  , orthogonal with respect to
, orthogonal with respect to  . Then,
. Then,  is holomorphic to first order if and only if
is holomorphic to first order if and only if  is both
is both  and
and  -holomorphic to first order.
-holomorphic to first order.
Proof.
Assume that  is holomorphic to first order. Then,
is holomorphic to first order. Then,  is
is  -holomorphic. As for (4.7), letting
-holomorphic. As for (4.7), letting  denote an arbitrary section of
denote an arbitrary section of  and
and  its projection into
its projection into  , we have
, we have

which is true since  is
is  -holomorphic to first order. Hence,
-holomorphic to first order. Hence,  is
is  -holomorphic to first order. Changing
-holomorphic to first order. Changing  to
to  shows that
shows that  is
is  -holomorphic to first order. The converse also follows using analogous arguments.
-holomorphic to first order. The converse also follows using analogous arguments.
Remark 4.4.
The importance of choosing the Levi-Civita connection on  is illusory. In particular, we can define the concept of holomorphicity to first order (or
is illusory. In particular, we can define the concept of holomorphicity to first order (or ,
, -holomorphicity to first order) for maps defined between almost complex manifolds, not necessarily equipped with any metric.
-holomorphicity to first order) for maps defined between almost complex manifolds, not necessarily equipped with any metric.
Indeed, let  be a holomorphic to first-order map with respect to
be a holomorphic to first-order map with respect to  , so that (4.6) holds. Let
, so that (4.6) holds. Let  denote a (local) frame for
denote a (local) frame for  . Then,
. Then,

Since  is holomorphic to first order,
is holomorphic to first order,  is holomorphic, the above equation is equivalent to
is holomorphic, the above equation is equivalent to

Now, since  holomorphicity does not depend on the chosen connection, we can deduce that holomorphicity with respect to
holomorphicity does not depend on the chosen connection, we can deduce that holomorphicity with respect to  reduces to the same condition (4.10). Thus,
reduces to the same condition (4.10). Thus,  being holomorphic to first order does not depend on the chosen connection. For
being holomorphic to first order does not depend on the chosen connection. For  (resp.,
(resp.,  ) holomorphicity to first order, we use similar arguments, replacing
) holomorphicity to first order, we use similar arguments, replacing  for a horizontal (resp., vertical) frame.
for a horizontal (resp., vertical) frame.
4.3. The 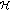 -Holomorphic Case
-Holomorphic Case
In the nonparametric case, given a conformal map  , we can always find a lift
, we can always find a lift  such that
such that  is holomorphic with respect to
is holomorphic with respect to  . In other words, (locally defined) strictly compatible lifts always exist. In general, this lift may not be
. In other words, (locally defined) strictly compatible lifts always exist. In general, this lift may not be  or
or  -holomorphic but it is
-holomorphic but it is  -holomorphic. Let
-holomorphic. Let  be a variation of
be a variation of  , conformal to first order. Then, if a lift
, conformal to first order. Then, if a lift  to the twistor space that makes
to the twistor space that makes  holomorphic for all small
holomorphic for all small  exists,
exists,  is necessarily conformal for all small
is necessarily conformal for all small  , which may not be the case. So, even if conformality is preserved to first order, there might be no strictly compatible twistor lift for all
, which may not be the case. So, even if conformality is preserved to first order, there might be no strictly compatible twistor lift for all  ; hence, we should relax the condition on conformality. We shall say that a twistor lift
; hence, we should relax the condition on conformality. We shall say that a twistor lift  of a conformal to first order map
of a conformal to first order map  is compatible to first order (with
is compatible to first order (with  ) if
) if

We start with a technical lemma, whose proof the reader can find in Section 5.
Lemma 4.5.
Let  be a conformal to first-order map. Let
be a conformal to first-order map. Let  be a twistor lift compatible to first order with
be a twistor lift compatible to first order with  . Then for all
. Then for all  there is a function
there is a function  and a vector field
and a vector field  with
with  ,
,  and
and  ,
,  such that
such that

In particular,  is
is  -holomorphic to first order in the sense that
-holomorphic to first order in the sense that

Lemma 4.6.
Let  be
be  -holomorphic to first order. Then,
-holomorphic to first order. Then,  is
is  -holomorphic to first order.
-holomorphic to first order.
Proof.
Since  is
is  -holomorphic to first order,
-holomorphic to first order,  . Therefore, for all
. Therefore, for all  , since
, since  is
is  -holomorphic,
-holomorphic,

Since  is a
is a  -holomorphic Riemannian submersion, the above equation can be written as
-holomorphic Riemannian submersion, the above equation can be written as

Hence, for all  , using the fact that
, using the fact that  is
is  holomorphic,
holomorphic,

showing that  and concluding our proof.
and concluding our proof.
Proposition 4.7.
Let  be
be  -holomorphic to first order map. Then, the projected map
-holomorphic to first order map. Then, the projected map  is conformal to first order. Conversely, let
is conformal to first order. Conversely, let  be a conformal to first order map. Then there is a (local)
be a conformal to first order map. Then there is a (local)  -holomorphic to first order map
-holomorphic to first order map  which is compatible to first order with
which is compatible to first order with  .
.
Proof.
Take  an
an  -holomorphic to first order map and let
-holomorphic to first order map and let  . We know that
. We know that  is conformal (Proposition 3.2). As for the first-order variation, using the preceding Lemma 4.6,
is conformal (Proposition 3.2). As for the first-order variation, using the preceding Lemma 4.6,

Using similar arguments, we can show that

concluding the first part of the proof.
Conversely, let  be any twistor lift of
be any twistor lift of  compatible to first order. Then, there is a function
compatible to first order. Then, there is a function  and a vector field
and a vector field  verifying the conditions on Lemma 4.5 with
verifying the conditions on Lemma 4.5 with

Now,  is
is  -holomorphic to first order if and only if
-holomorphic to first order if and only if  is
is  -holomorphic (which follows from Proposition 3.2) and (4.6) holds. Using the same argument as in Lemma 4.3, (4.6) is equivalent to
-holomorphic (which follows from Proposition 3.2) and (4.6) holds. Using the same argument as in Lemma 4.3, (4.6) is equivalent to

But

from the given conditions on  and
and  and thus concluding the proof.
and thus concluding the proof.
4.4. The  -Holomorphic Case
-Holomorphic Case
Next, we give a useful characterization for maps to be  -holomorphic to first order (
-holomorphic to first order ( or
or  ), whose proof is in Section 5 (compare with Proposition 3.3).
), whose proof is in Section 5 (compare with Proposition 3.3).
Lemma 4.8.
Let  be a smooth map and let
be a smooth map and let  be its projection. Then,
be its projection. Then,  is
is  -holomorphic to first order (
-holomorphic to first order ( or
or  ) if and only if
) if and only if


or

From the preceding lemma, we can also deduce the following.
Lemma 4.9.
Let  be a map
be a map  -holomorphic to first order and consider the projected map
-holomorphic to first order and consider the projected map  . Then for all
. Then for all  there is
there is  with
with

Proof.
For  , we have
, we have  so that using (4.22) we have
so that using (4.22) we have

Taking  , we obtain the result. To establish an induction, assume now that the result is valid for
, we obtain the result. To establish an induction, assume now that the result is valid for  ; that is, there is
; that is, there is  such that
such that

Taking  and noticing that
and noticing that  ,
,

as  is antisymmetric on the first two arguments. Now, since
is antisymmetric on the first two arguments. Now, since  is
is  -holomorphic, (4.23) holds so that there is
-holomorphic, (4.23) holds so that there is  such that
such that

But the second condition gives  , whereas the first holds precisely that
, whereas the first holds precisely that  , as we wanted to show.
, as we wanted to show.
Proposition 4.10 (projections of maps  -holomorphic to first order).
-holomorphic to first order).
Let  be a map
be a map  -holomorphic to first order, where
-holomorphic to first order, where  is any Riemann surface. Then, the projection map
is any Riemann surface. Then, the projection map  is isotropic to first order.
is isotropic to first order.
Notice that we could replace  with
with  , as real isotropy (to first order) does not depend on the fixed orientation on
, as real isotropy (to first order) does not depend on the fixed orientation on  .
.
Proof.
That  is isotropic follows from the nonparametric case. Therefore, we are left with proving that
is isotropic follows from the nonparametric case. Therefore, we are left with proving that

Using Lemma 4.9, for fixed  , choose
, choose  with
with  and
and  . Then, the conclusion follows from
. Then, the conclusion follows from

We now turn our attention to the existence of lifts  -holomorphic to first order for a given isotropic to first-order map
-holomorphic to first order for a given isotropic to first-order map  . Recall that in the nonparametric case such lift exists (see Remark 3.4).
. Recall that in the nonparametric case such lift exists (see Remark 3.4).
Theorem 4.11.
Let  be an isotropic to first order with
be an isotropic to first order with  and
and  linearly independent. Then, there is either a (local) map
linearly independent. Then, there is either a (local) map  or a map
or a map  which is
which is  -holomorphic to first order and compatible to first order with
-holomorphic to first order and compatible to first order with  .
.
Before proving Theorem 4.11, we give the following lemma, which we prove in Section 5
Lemma 4.12.
Let  be as in the preceding Theorem 4.11.
be as in the preceding Theorem 4.11.
(i)Suppose that the  -holomorphic lift of
-holomorphic lift of  is
is  (resp.,
(resp.,  ). Take
). Take  the unique positive (resp., negative) almost Hermitian structure on
the unique positive (resp., negative) almost Hermitian structure on  compatible with
compatible with  . Then, taking
. Then, taking

we have that

(ii)There are  ,
,  such that
such that

We are now ready to prove Theorem 4.11.
Proof of Theorem 4.11.
As before, take  or
or  the
the  -holomorphic lift of
-holomorphic lift of  . Assume, without loss of generality, that it is
. Assume, without loss of generality, that it is  . Then, at each
. Then, at each  take
take  the unique positive almost Hermitian structure compatible with
the unique positive almost Hermitian structure compatible with  and let us prove that this map
and let us prove that this map  is
is  -holomorphic to first order. Using Lemma 4.5,
-holomorphic to first order. Using Lemma 4.5,  is
is  -holomorphic to first order and we are left with proving that (4.23) holds. It is enough to prove that there is a basis
-holomorphic to first order and we are left with proving that (4.23) holds. It is enough to prove that there is a basis  of
of  for which (4.23) holds. Now, take
for which (4.23) holds. Now, take  and
and  where
where  is as in (4.32). Then,
is as in (4.32). Then,

Analogously,

where we have used  ,
,  ,
,  , and
, and  . Hence,
. Hence,  and
and  satisfy equation (4.23), concluding our proof.
satisfy equation (4.23), concluding our proof.
4.5. The 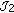 Holomorphic Case
Holomorphic Case
We prove the following.
Theorem 4.13.
Let  be a map
be a map  -holomorphic to first order. Then,
-holomorphic to first order. Then,  is harmonic to first order (and conformal to first order from Lemma 4.3 and Proposition 4.7).
is harmonic to first order (and conformal to first order from Lemma 4.3 and Proposition 4.7).
We first give the following characterization of  -holomorphic to first order maps.
-holomorphic to first order maps.
Lemma 4.14.
Let  (
( or
or  ) be a smooth map. Then,
) be a smooth map. Then,  is a
is a  -holomorphic to first order map if and only if
-holomorphic to first order map if and only if  is
is  -holomorphic and
-holomorphic and

Proof.
If  is any smooth map, then [17]
is any smooth map, then [17]  . Hence, from (2.9),
. Hence, from (2.9),

Thus, we can rephrase equation (4.37) as

which is the condition for  -holomorphicity.
-holomorphicity.
Proof of Theorem 4.13.
That  is harmonic follows from Theorem 3.1. Hence, we are left with proving that
is harmonic follows from Theorem 3.1. Hence, we are left with proving that  . Since
. Since  is
is  -holomorphic to first order, we deduce that
-holomorphic to first order, we deduce that  is both
is both  and
and  -holomorphic to first order (Lemma 4.3). From
-holomorphic to first order (Lemma 4.3). From  -holomorphicity (4.37), we have
-holomorphicity (4.37), we have

Using Lemma 4.6 and (4.13) together with symmetry of the second fundamental form of  , the right-hand side of the above identity becomes
, the right-hand side of the above identity becomes

so that  , concluding the proof.
, concluding the proof.
Theorem 4.15.
Let  be a harmonic and conformal to first order map. Then, there is (locally) a map
be a harmonic and conformal to first order map. Then, there is (locally) a map  which is
which is  -holomorphic to first order and with
-holomorphic to first order and with  .
.
Since harmonicity (to first order) does not depend on the orientation on  , we could have replaced
, we could have replaced  by
by  in both Theorems 4.13 and 4.15
in both Theorems 4.13 and 4.15
Proof.
For each  consider
consider  , bundle over
, bundle over  . Since
. Since  is a Riemann surface,
is a Riemann surface,  and we can conclude that for each
and we can conclude that for each  there is a Koszul-Malgrange holomorphic structure on
there is a Koszul-Malgrange holomorphic structure on  . Hence ([16, Theorem
. Hence ([16, Theorem  .]), there is a smooth section
.]), there is a smooth section  with
with  a Koszul-Malgrange holomorphic section of
a Koszul-Malgrange holomorphic section of  :
:  . So,
. So,

equivalently,

Take  where
where  is the
is the  -part on
-part on  determined by
determined by  = rotation by +
= rotation by + on
on  (
( ). (Notice that as
). (Notice that as  is not conformal we might not get a Hermitian structure by setting
is not conformal we might not get a Hermitian structure by setting  ; on the other hand, positive rotation by
; on the other hand, positive rotation by  comes from the natural orientation on
comes from the natural orientation on  imported from
imported from  via
via .) Then
.) Then  defines a compatible twistor lift of
defines a compatible twistor lift of  . Let us check that
. Let us check that  is
is  -holomorphic to first order. That
-holomorphic to first order. That  is holomorphic is immediate. From the proof of Proposition 4.7, we deduce that
is holomorphic is immediate. From the proof of Proposition 4.7, we deduce that  is
is  -holomorphic to first order as it is compatible to first order with
-holomorphic to first order as it is compatible to first order with  and the latter is conformal to first order. Hence, we are left with proving that (4.37)
and the latter is conformal to first order. Hence, we are left with proving that (4.37)

holds. We shall establish this equation by showing that both sides agree when applied to any vector  . For that, we consider, in turn, the three cases
. For that, we consider, in turn, the three cases  ,
,  , and
, and  . The first two have similar arguments so that we prove only the first.
. The first two have similar arguments so that we prove only the first.
(i) . From
. From  holomorphicity, we have
holomorphicity, we have  . On the other hand, as
. On the other hand, as  is
is  -holomorphic to first order, (4.13) is satisfied. Finally, for all
-holomorphic to first order, (4.13) is satisfied. Finally, for all  ,
,

Since  is harmonic to first order, our condition follows from
is harmonic to first order, our condition follows from

(ii) . We now have
. We now have

Now, the first condition follows from (4.43) since  is Koszul-Malgrange holomorphic for each
is Koszul-Malgrange holomorphic for each  . As for the second, letting
. As for the second, letting  denote its left-hand side, we shall prove that
denote its left-hand side, we shall prove that  for all
for all  . We do this by establishing the three cases
. We do this by establishing the three cases  ,
,  and
and  (since the first two cases have similar arguments, we prove only the first).
(since the first two cases have similar arguments, we prove only the first).
( )When  we have
we have

( )Let  . Then,
. Then,

The first term on the right side of the above equation vanishes as  lies in
lies in  , whereas the second is zero from
, whereas the second is zero from  -holomorphicity, concluding our proof.
-holomorphicity, concluding our proof.
4.6. The 4-Dimensional Case
Theorem 4.16.
Let  be harmonic and isotropic to first-order map and with
be harmonic and isotropic to first-order map and with  and
and  being linearly independent. Then, (locally) there is either a map
being linearly independent. Then, (locally) there is either a map  or a map
or a map  which is simultaneously
which is simultaneously  and
and  -holomorphic to first order and with
-holomorphic to first order and with  . Conversely, if
. Conversely, if  (or
(or  ) is
) is  and
and  -holomorphic to first order, the projected map
-holomorphic to first order, the projected map  is harmonic and isotropic to first order.
is harmonic and isotropic to first order.
Proof.
The converse is obvious from Proposition 4.10 and Theorem 4.13. As for the first part, in Theorem 4.11 we saw that we can lift the map  to a map
to a map  -holomorphic to first order. Moreover, this lift could be defined as the unique positive or negative almost complex structure compatible with
-holomorphic to first order. Moreover, this lift could be defined as the unique positive or negative almost complex structure compatible with  . On the other hand, in Theorem 4.15 we have seen that there is a map
. On the other hand, in Theorem 4.15 we have seen that there is a map  -holomorphic to first order with
-holomorphic to first order with  and for which
and for which  is compatible. From the comment after Theorem 4.15, there is also a twistor lift of
is compatible. From the comment after Theorem 4.15, there is also a twistor lift of  into
into  . Therefore, from the dimension of
. Therefore, from the dimension of  , we conclude that the lifts constructed in both cited results are the same and, therefore, simultaneously
, we conclude that the lifts constructed in both cited results are the same and, therefore, simultaneously  and
and  -holomorphic to first order.
-holomorphic to first order.
We would now like to guarantee the uniqueness to first order of our twistor lift. Before stating such a result, we start with a lemma, proved in Section 5.
Lemma 4.17.
Let  be a map
be a map  -holomorphic to first order. Consider the twistor projection
-holomorphic to first order. Consider the twistor projection  and the vectors
and the vectors  and
and  defined by
defined by

so that

Then, for all  for which
for which  and
and  are linearly independent
are linearly independent

Notice that in Lemma 4.12, we were given  and defined the twistor lift as the unique lift compatible with
and defined the twistor lift as the unique lift compatible with  . Now, we are given the twistor map
. Now, we are given the twistor map  but nothing guarantees that projecting the map to
but nothing guarantees that projecting the map to  makes
makes  compatible; that is,
compatible; that is,  may not preserve
may not preserve  .
.
Proposition 4.18.
Let  be two
be two  -holomorphic to first-order maps such that
-holomorphic to first-order maps such that  and the variational vector fields induced on
and the variational vector fields induced on  are the same; that is, writing
are the same; that is, writing  ,
,  , we have
, we have  . Then, at all points
. Then, at all points  for which
for which  and
and  are linearly independent, writing
are linearly independent, writing  ,
,  , we have
, we have  .
.
Proof.
Let  (
( ) denote the projection maps. From our hypothesis, it follows that
) denote the projection maps. From our hypothesis, it follows that  . Hence, the only thing left is to prove that the vertical parts coincide. Now, from the proof of Lemma 4.14,
. Hence, the only thing left is to prove that the vertical parts coincide. Now, from the proof of Lemma 4.14,  so that our result follows if
so that our result follows if  . We prove this identity showing that
. We prove this identity showing that  for all
for all  , where
, where

We consider the four possible cases for  ; namely, when
; namely, when  is equal to
is equal to  ,
,  ,
,  or
or  , where
, where  and
and  are as in the preceding lemma (notice that, since
are as in the preceding lemma (notice that, since  , then
, then  and
and  ).
).
(i)When  (
( uses similar arguments), we have
uses similar arguments), we have

where we have used Lemma 4.17, as well as the fact that  and
and  .
.
(ii)Taking  (
( uses similar arguments), we have
uses similar arguments), we have

But

As  , we deduce
, we deduce  ; analogously,
; analogously,  so that
so that  .
.
Hence, the twistor lifts constructed in Theorem 4.16 are unique to first order, in the sense that the vector field  induced on
induced on  (or
(or  ) by the map
) by the map  ,
,  depends only on the initial projected map
depends only on the initial projected map  and on the Jacobi field
and on the Jacobi field  along
along  . Moreover, taking
. Moreover, taking  the
the  -sphere or the complex projective plane, letting
-sphere or the complex projective plane, letting  be a harmonic map, and
be a harmonic map, and  a Jacobi field, isotropy to first order is immediately guaranteed. Hence, the previous construction allows a (local) unified proof of the twistor correspondence between Jacobi fields and twistor vector fields that are tangent to variations on
a Jacobi field, isotropy to first order is immediately guaranteed. Hence, the previous construction allows a (local) unified proof of the twistor correspondence between Jacobi fields and twistor vector fields that are tangent to variations on  which are simultaneously
which are simultaneously  and
and  -holomorphic (infinitesimal horizontal holomorphic deformations in [5]). We can also conclude which different properties (namely, conformality, real isotropy or harmonicity) are related with those of the twistor lift (resp.,
-holomorphic (infinitesimal horizontal holomorphic deformations in [5]). We can also conclude which different properties (namely, conformality, real isotropy or harmonicity) are related with those of the twistor lift (resp.,  ,
,  or
or  -holomorphicity).
-holomorphicity).
5. Additional Proofs
Proof of Lemma 4.5.
Since  is compatible to first order,
is compatible to first order,  preserves
preserves  for all
for all  . Hence, there are
. Hence, there are  and
and  such that
such that

Take  . Since, at
. Since, at  ,
,  we deduce
we deduce  and
and  . Now, since
. Now, since  and
and  form an orthogonal basis for
form an orthogonal basis for  , we have
, we have

Differentiating with respect to  at the point
at the point  , the above identity yields
, the above identity yields

Computing the inner product of (5.1) with  and using the fact that
and using the fact that  vanishes for all
vanishes for all  , we get
, we get  . Hence,
. Hence,

and we deduce  , as
, as  and (5.3) hold. Using (5.1) again, we can now write
and (5.3) hold. Using (5.1) again, we can now write

which vanishes since  for all
for all  , the second and last terms cancelling as
, the second and last terms cancelling as  is
is  -holomorphic and
-holomorphic and  is conformal to first order. Analogously,
is conformal to first order. Analogously,  vanishes so that
vanishes so that  . For the orthogonal part, taking
. For the orthogonal part, taking  ,
,

showing that  and concluding the proof.
and concluding the proof.
Proof of Lemma 4.8.
We shall do the proof only for the  case, with the
case, with the  case being similar. Assume that
case being similar. Assume that  is
is  -holomorphic to first order. Then, using Lemmas 4.3 and 4.6,
-holomorphic to first order. Then, using Lemmas 4.3 and 4.6,  is
is  -holomorphic to first order. On the other hand,
-holomorphic to first order. On the other hand,  satisfies equation (4.37), which implies that for all
satisfies equation (4.37), which implies that for all 

Take  in
in  . Let
. Let  be such that
be such that  and write
and write  . Then,
. Then,

Moreover, since  is holomorphic,
is holomorphic,  and
and

finishing the first part of our proof.
Conversely, suppose that (4.22) and (4.23) hold. Take  and
and  with
with  and
and  . Then
. Then

and we can now easily conclude that (5.7) holds. Together with the fact that  is
is  -holomorphic (Proposition 3.3), we can conclude that (4.37) is verified. As for the horizontal part, we have that
-holomorphic (Proposition 3.3), we can conclude that (4.37) is verified. As for the horizontal part, we have that

as  is holomorphic. Since (4.22) holds, the last condition is trivially satisfied and we can conclude that our map is
is holomorphic. Since (4.22) holds, the last condition is trivially satisfied and we can conclude that our map is  -holomorphic to first order, as desired.
-holomorphic to first order, as desired.
Proof of Lemma 4.12.
-
(i)
Since
 is isotropic to first order,
is isotropic to first order, 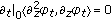 , equivalently,
, equivalently, 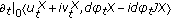 . Thus, we have
. Thus, we have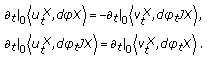 (5.12)
(5.12)
Similarly,  is equivalent to
is equivalent to  and implies
and implies

As  is compatible with
is compatible with  , Lemma 4.5 guarantees that
, Lemma 4.5 guarantees that  is
is  -holomorphic to first order. On the other hand, since
-holomorphic to first order. On the other hand, since  and
and  are linearly independent, we deduce that
are linearly independent, we deduce that  ,
,  and
and  form a basis for
form a basis for  . Hence, (4.33) will be satisfied if and only on evaluating the inner product of
. Hence, (4.33) will be satisfied if and only on evaluating the inner product of  and
and  with which one of these four vectors one obtains the same result. We shall only prove for the first and fourth vectors, the other two cases being similar.
with which one of these four vectors one obtains the same result. We shall only prove for the first and fourth vectors, the other two cases being similar.
(a)Since  ,
,

(b)Using (5.13),

-
(ii)
We know that
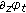 ,
,  ,
,  ,
, 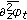 span
span 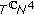 . Hence, there are
. Hence, there are  , and
, and 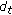 with
with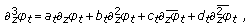 (5.16)
(5.16)
where  since
since  . Therefore,
. Therefore,

Now, using the fact that  is isotropic to first order, we have
is isotropic to first order, we have

Together with

we deduce

Similarly, from

we have

Equations (5.20) and (5.22) imply that either  (which is absurd as
(which is absurd as  does not lie in
does not lie in  ) or
) or  and consequently (4.34) holds, as wanted.
and consequently (4.34) holds, as wanted.
Proof of Lemma 4.17.
That  follows from the proof of Proposition 4.7. Since
follows from the proof of Proposition 4.7. Since  , and
, and  are linearly independent vectors, we can deduce that
are linearly independent vectors, we can deduce that  ,
,  ,
,  and
and  form a basis for
form a basis for  for
for  is a neighbourhood of
is a neighbourhood of  . On the other hand, as
. On the other hand, as  is the projection of a map
is the projection of a map  -holomorphic to first order, we know that it must be isotropic to first order from Proposition 4.10. Hence,
-holomorphic to first order, we know that it must be isotropic to first order from Proposition 4.10. Hence,

The argument to establish the second and third identities in (4.52), will now be similar to the one in Lemma 4.12(i).
References
Burstall FE, Lemaire L, Rawnsley JH: Harmonic maps bibliography. http://people.bath.ac.uk/masfeb/harmonic.html
Eells J, Lemaire L: A report on harmonic maps. The Bulletin of the London Mathematical Society 1978, 10(1):1–68. 10.1112/blms/10.1.1
Eells J, Lemaire L: Another report on harmonic maps. The Bulletin of the London Mathematical Society 1988, 20(5):385–524. 10.1112/blms/20.5.385
Lemaire L, Wood JC: Jacobi fields along harmonic 2-spheres in are integrable. Journal of the London Mathematical Society. Second Series 2002, 66(2):468–486. 10.1112/S0024610702003496
Lemaire L, Wood JC: Jacobi fields along harmonic 2-spheres in 3- and 4-spheres are not all integrable. The Tohoku Mathematical Journal. Second Series 2009, 61(2):165–204.
Salamon S: Harmonic and holomorphic maps. In Geometry Seminar, Lecture Notes in Mathematics. Volume 1164. Springer, Berlin, Germany; 1985:161–224. 10.1007/BFb0081912
Koszul J-L, Malgrange B: Sur certaines structures fibrées complexes. Archiv der Mathematik 1958, 9: 102–109. 10.1007/BF02287068
Simões BA, Svensson M: Twistor spaces, pluriharmonic maps and harmonic morphisms. The Quarterly Journal of Mathematics 2009, 60(3):367–385. 10.1093/qmath/han019
Atiyah MF, Hitchin NJ, Singer IM: Self-duality in four-dimensional Riemannian geometry. Proceedings of the Royal Society A 1978, 362(1711):425–461. 10.1098/rspa.1978.0143
O'Brian NR, Rawnsley JH: Twistor spaces. Annals of Global Analysis and Geometry 1985, 3(1):29–58. 10.1007/BF00054490
Davidov J, Sergeev AG: Twistor spaces and harmonic maps. Uspekhi Matematicheskikh Nauk 1993, 48(3):3–96. English translation in Russian Mathematical Surveys, vol. 48, no. 3, pp. 1–91, 1993
Calabi E: Quelques applications de l'analyse complexe aux surfaces d'aire minima. In Topics in Complex Manifolds. Université de Montréal, Montreal, Canada; 1967:59–81.
Rawnsley JH: -structures, -twistor spaces and harmonic maps. In Geometry Seminar, Lecture Notes in Mathematics. Volume 1164. Springer, Berlin, Germany; 1985:85–159. 10.1007/BFb0081911
Chern SS: On the minimal immersions of the two-sphere in a space of constant curvature. In Problems in Analysis. Edited by: Gunning RC. Princeton University Press, Princeton, NJ, USA; 1970:27–40.
Wood JC: Jacobi fields along harmonic maps. In Differential Geometry and Integrable Systems (Proceedings of the 9th MSJ-IRI, Tokyo, 2000), Contemporary Mathematics. Volume 308. American Mathematical Society, Providence, RI, USA; 2002:329–340.
Simões BA: Twistorial constructions of harmonic morphisms and Jacobi fields, Ph.D. thesis. University of Leeds, Leeds, UK; 2007.
Eells J, Salamon S: Twistorial construction of harmonic maps of surfaces into four-manifolds. Annali della Scuola Normale Superiore di Pisa. Classe di Scienze. Serie IV 1985, 12(4):589–640.
Acknowledgments
The author is grateful to Professor J. C. Wood for helpful comments and stimulating discussions during the preparation of this work. The author would also like to thank the referee for valuable comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Simões, B.A. First-Order Twistor Lifts. J Inequal Appl 2010, 594843 (2010). https://doi.org/10.1155/2010/594843
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/594843
 -Holomorphic Case
-Holomorphic Case -Holomorphic Case
-Holomorphic Case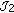 Holomorphic Case
Holomorphic Case is isotropic to first order,
is isotropic to first order, 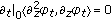 , equivalently,
, equivalently, 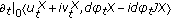 . Thus, we have
. Thus, we have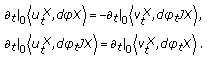
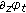 ,
,  ,
,  ,
, 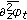 span
span 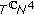 . Hence, there are
. Hence, there are  , and
, and 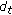 with
with