- Research Article
- Open access
- Published:
Some Identities on the Generalized 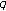 -Bernoulli Numbers and Polynomials Associated with
-Bernoulli Numbers and Polynomials Associated with 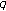 -Volkenborn Integrals
-Volkenborn Integrals
Journal of Inequalities and Applications volume 2010, Article number: 575240 (2010)
Abstract
We give some interesting equation of  -adic
-adic  -integrals on
-integrals on  . From those
. From those  -adic
-adic  -integrals, we present a systemic study of some families of extended Carlitz type
-integrals, we present a systemic study of some families of extended Carlitz type  -Bernoulli numbers and polynomials in
-Bernoulli numbers and polynomials in  -adic number field.
-adic number field.
1. Introduction
Let  be a fixed prime number. Throughout this paper,
be a fixed prime number. Throughout this paper,  ,
,  ,
,  , and
, and  will, respectively, denote the ring of
will, respectively, denote the ring of  -adic rational integer, the field of
-adic rational integer, the field of  -adic rational numbers, the complex number field, and the completion of algebraic closure of
-adic rational numbers, the complex number field, and the completion of algebraic closure of  . Let
. Let  be the set of natural numbers and
be the set of natural numbers and  .
.
Let  be the normalized exponential valuation of
be the normalized exponential valuation of  with
with  When one talks of
When one talks of  -extension,
-extension,  is considered as an indeterminate, a complex number
is considered as an indeterminate, a complex number  or
or  -adic number
-adic number  If
If  , we normally assume that
, we normally assume that  , and if
, and if  we normally assume that
we normally assume that  . We use the notation
. We use the notation

The  -factorial is defined as
-factorial is defined as

and the Gaussian  -binomial coefficient is defined by
-binomial coefficient is defined by

(see [1]). Note that

From (1.3), we easily see that

(see [2, 3]). For a fixed positive integer  , let
, let

We say that  is a uniformly differential function at a point
is a uniformly differential function at a point  and denote this property by
and denote this property by  if the difference quotients
if the difference quotients

have a limit  as
as  . For
. For  , let us begin with the expression
, let us begin with the expression

representing a  -analogue of the Riemann sums for
-analogue of the Riemann sums for  , (see [1–3, 11–18]). The integral of
, (see [1–3, 11–18]). The integral of  on
on  is defined as the limit
is defined as the limit  of the sums (if exists). The
of the sums (if exists). The  -adic
-adic  -integral (=
-integral (=  -Volkenborn integral) of
-Volkenborn integral) of  ) is defined by
) is defined by

(see [12]). Carlitz's  -Bernoull numbers
-Bernoull numbers  can be defined recursively by
can be defined recursively by  and by the rule that
and by the rule that

with the usual convention of replacing  by
by  , (see [1–13]).
, (see [1–13]).
It is well known that

(see [1]), where  are called the
are called the  th Carlitz's
th Carlitz's  -Bernoulli polynomials (see [1, 12, 13]).
-Bernoulli polynomials (see [1, 12, 13]).
Let  be the Dirichlet's character with conductor
be the Dirichlet's character with conductor  , then the generalized Carlitz's
, then the generalized Carlitz's  -Bernoulli numbers attached to
-Bernoulli numbers attached to  are defined as follows:
are defined as follows:

(see [13]). Recently, many authors have studied in the different several areas related to  -theory (see [1–13]). In this paper, we present a systemic study of some families of multiple Carlitz's type
-theory (see [1–13]). In this paper, we present a systemic study of some families of multiple Carlitz's type  -Bernoulli numbers and polynomials by using the integral equations of
-Bernoulli numbers and polynomials by using the integral equations of  -adic
-adic  -integrals on
-integrals on  . First, we derive some interesting equations of
. First, we derive some interesting equations of  -adic
-adic  -integrals on
-integrals on  . From these equations, we give some interesting formulae for the higher-order Carlitz's type
. From these equations, we give some interesting formulae for the higher-order Carlitz's type  -Bernoulli numbers and polynomials in the
-Bernoulli numbers and polynomials in the  -adic number field.
-adic number field.
2. On the Generalized Higher-Order  -Bernoulli Numbersand Polynomials
-Bernoulli Numbersand Polynomials
In this section, we assume that  with
with  . We first consider the
. We first consider the  -extension of Bernoulli polynomials as follows:
-extension of Bernoulli polynomials as follows:

From (2.1), we note that

Note that

where  are called the
are called the  th ordinary Bernoulli polynomials. In the special case,
th ordinary Bernoulli polynomials. In the special case,  ,
,  are called the
are called the  th
th  -Bernoulli numbers.
-Bernoulli numbers.
By (2.2), we have the following lemma.
Lemma 2.1.
For  one has
one has

Now, one considers the  -Bernoulli polynomials of order
-Bernoulli polynomials of order  as follows:
as follows:

By (2.5), one sees that

In the special case,  , the sequence
, the sequence  is refereed to as the
is refereed to as the  -extension of Bernoulli numbers of order
-extension of Bernoulli numbers of order  . For
. For  , one has
, one has

By (2.5) and (2.7), one obtains the following theorem.
Theorem 2.2.
For  one has
one has

Let  be the primitive Dirichlet's character with conductor
be the primitive Dirichlet's character with conductor  , then the generalized
, then the generalized  -Bernoulli polynomials attached to
-Bernoulli polynomials attached to  are defined by
are defined by

From (2.9), one derives

By (2.9) and (2.10), one can give the generating function for the generalized  -Bernoulli polynomials attached to
-Bernoulli polynomials attached to  as follows:
as follows:

From (1.3), (2.10), and (2.11), one notes that

In the special case,  , the sequence
, the sequence  are called the
are called the  th generalized
th generalized  -Bernoulli numbers attached to
-Bernoulli numbers attached to  .
.
Let one consider the higher-order  -Bernoulli polynomials attached to
-Bernoulli polynomials attached to  as follows:
as follows:

where  are called the
are called the  th generalized
th generalized  -Bernoulli polynomials of order
-Bernoulli polynomials of order  attaches to
attaches to  .
.
By (2.13), one sees that

In the special case,  , the sequence
, the sequence  are called the
are called the  th generalized
th generalized  -Bernoulli numbers of order
-Bernoulli numbers of order  attaches to
attaches to  .
.
By (2.13) and (2.14), one obtains the following theorem.
Theorem 2.3.
Let  be the primitive Dirichlet's character with conductor
be the primitive Dirichlet's character with conductor  . For
. For  one has
one has

For  , and
, and  one introduces the extended higher-order
one introduces the extended higher-order  -Bernoulli polynomials as follows:
-Bernoulli polynomials as follows:

From (2.16), one notes that

and

In the special case,  ,
,  are called the
are called the  th
th  -Bernoulli numbers of order
-Bernoulli numbers of order  .
.
By (2.17), one obtains the following theorem.
Theorem 2.4.
For  one has
one has

Let  be the primitive Dirichlet's character with conductor
be the primitive Dirichlet's character with conductor  , then one considers the generalized
, then one considers the generalized  -Bernoulli polynomials attached to
-Bernoulli polynomials attached to  of order
of order  as follows:
as follows:

By (2.20), one sees that

In the special case,  ,
,  are called the
are called the  th generalized
th generalized  -Bernoulli numbers attached to
-Bernoulli numbers attached to  of order
of order  .
.
From (2.20) and (2.21), one notes that

By (2.16), it is easy to show that

Thus, one has

From (2.16) and (2.23), one can also derive

It is easy to see that

By (2.23), (2.25), and (2.26), one obtains the following theorem.
Theorem 2.5.
For  and
and  one has
one has

Furthermore, one gets

Now, one considers the polynomials of  by
by

By (2.29), one obtains the following theorem.
Theorem 2.6.
For  and
and  one has
one has

By using multivariate  -adic
-adic  -integral on
-integral on  , one sees that
, one sees that

Therefore, one obtains the following corollary.
Corollary 2.7.
For  and
and  one has
one has

It is easy to show that

From (2.33), one notes that

From the multivariate  -adic
-adic  -integral on
-integral on  , one has
, one has


By (2.35) and (2.36), one obtains the following corollary.
Corollary 2.8.
For  and
and  one has
one has

Now, one also considers the polynomial of  . From the integral equation on
. From the integral equation on  , one notes that
, one notes that

By (2.38), one easily gets

Thus, one obtains the following theorem.
Theorem 2.9.
For  and
and  one has
one has

From the definition of  -adic
-adic  -integral on
-integral on  , one notes that
, one notes that

Thus, one has

By (2.38), one easily gets

From (2.43), one has

That is,

By (2.38) and (2.43), one easily sees that

and

For  , this gives
, this gives

and

From (2.46) and (2.48), one can derive the recurrence relation for  as follows:
as follows:

where  is kronecker symbol.
is kronecker symbol.
By (2.46), (2.48), and (2.50), one obtains the following theorem.
Theorem 2.10.
For  and
and  one has
one has

Furthermore,

where  is kronecker symbol.
is kronecker symbol.
From the definition of  -adic
-adic  -integral on
-integral on  , one notes that
, one notes that

By (2.53), one sees that

Note that

where  are the
are the  th ordinary Bernoulli polynomials.
th ordinary Bernoulli polynomials.
In the special case,  , one gets
, one gets

It is not difficult to show that

That is,

Let one consider Barnes' type multiple  -Bernoulli polynomials. For
-Bernoulli polynomials. For  and
and  one defines Barnes' type multiple
one defines Barnes' type multiple  -Bernoulli polynomials as follows:
-Bernoulli polynomials as follows:

From (2.59), one can easily derive the following equation:

Let  , then one has
, then one has

Therefore, one obtains the following theorem.
Theorem 2.11.
For  and
and  one has
one has

References
Kim T: -Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008, 15(1):51–57.
Kim T: Barnes-type multiple -zeta functions and -Euler polynomials. Journal of Physics A: Mathematical and Theoretical 2010, 43(25):-11.
Kim T: Note on the Euler -zeta functions. Journal of Number Theory 2009, 129(7):1798–1804. 10.1016/j.jnt.2008.10.007
Carlitz L: -Bernoulli numbers and polynomials. Duke Mathematical Journal 1948, 15: 987–1000. 10.1215/S0012-7094-48-01588-9
Carlitz L: -Bernoulli and Eulerian numbers. Transactions of the American Mathematical Society 1954, 76: 332–350.
Cangul IN, Kurt V, Ozden H, Simsek Y: On the higher-order --Genocchi numbers. Advanced Studies in Contemporary Mathematics 2009, 19(1):39–57.
Cenkci M, Kurt V: Congruences for generalized -Bernoulli polynomials. Journal of Inequalities and Applications 2008, 2008:-19.
Govil NK, Gupta V: Convergence of -Meyer-König-Zeller-Durrmeyer operators. Advanced Studies in Contemporary Mathematics 2009, 19(1):97–108.
Jang L-C, Hwang K-W, Kim Y-H: A note on -Genocchi polynomials and numbers of higher order. Advances in Difference Equations 2010, 2010:-6.
Jang L-C: A new -analogue of Bernoulli polynomials associated with -adic -integrals. Abstract and Applied Analysis 2008, 2008:-6.
Kim T: Some identities on the -Euler polynomials of higher order and -Stirling numbers by the fermionic -adic integral on . Russian Journal of Mathematical Physics 2009, 16(4):484–491. 10.1134/S1061920809040037
Kim T: On a -analogue of the -adic log gamma functions and related integrals. Journal of Number Theory 1999, 76(2):320–329. 10.1006/jnth.1999.2373
Kim T: -Volkenborn integration. Russian Journal of Mathematical Physics 2002, 9(3):288–299.
Kurt V: A further symmetric relation on the analogue of the Apostol-Bernoulli and the analogue of the Apostol-Genocchi polynomials. Applied Mathematical Sciences 2009, 3(53–56):2757–2764.
Ozden H, Cangul IN, Simsek Y: Remarks on -Bernoulli numbers associated with Daehee numbers. Advanced Studies in Contemporary Mathematics 2009, 18(1):41–48.
Simsek Y: Generating functions of the twisted Bernoulli numbers and polynomials associated with their interpolation functions. Advanced Studies in Contemporary Mathematics 2008, 16(2):251–278.
Moon E-J, Rim S-H, Jin J-H, Lee S-J: On the symmetric properties of higher-order twisted -Euler numbers and polynomials. Advances in Difference Equations 2010, 2010:-8.
Ozden H, Simsek Y, Rim S-H, Cangul IN: A note on -adic -Euler measure. Advanced Studies in Contemporary Mathematics 2007, 14(2):233–239.
Acknowledgments
The authors express their gratitude to The referees for their valuable suggestions and comments. This paper was supported by the research grant of Kwangwoon University in 2010.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kim, T., Choi, J., Lee, B. et al. Some Identities on the Generalized 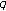 -Bernoulli Numbers and Polynomials Associated with
-Bernoulli Numbers and Polynomials Associated with 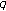 -Volkenborn Integrals.
J Inequal Appl 2010, 575240 (2010). https://doi.org/10.1155/2010/575240
-Volkenborn Integrals.
J Inequal Appl 2010, 575240 (2010). https://doi.org/10.1155/2010/575240
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/575240
 and
and  (see [
(see [ -Bernoulli Numbersand Polynomials
-Bernoulli Numbersand Polynomials