- Research Article
- Open access
- Published:
A Hájek-Rényi-Type Maximal Inequality and Strong Laws of Large Numbers for Multidimensional Arrays
Journal of Inequalities and Applications volume 2010, Article number: 569759 (2010)
Abstract
A Hájek-Rényi-type maximal inequality is established for multidimensional arrays of random elements. Using this result, we establish some strong laws of large numbers for multidimensional arrays. We also provide some characterizations of Banach spaces.
1. Introduction and Preliminaries
Throughout this paper, the symbol  will denote a generic positive constant which is not necessarily the same one in each appearance. Let
will denote a generic positive constant which is not necessarily the same one in each appearance. Let  be a positive integer, the set of all nonnegative integer
be a positive integer, the set of all nonnegative integer  -dimensional lattice points will be denoted by
-dimensional lattice points will be denoted by  , and the set of all positive integer
, and the set of all positive integer  -dimensional lattice points will be denoted by
-dimensional lattice points will be denoted by  . We will write
. We will write  ,
,  ,
,  , and
, and  for points
for points  ,
,  ,
,  , and
, and  , respectively. The notation
, respectively. The notation  (or
(or  ) means that
) means that  for all
for all  , the limit
, the limit  is interpreted as
is interpreted as  for all
for all  (this limit is equivalent to
(this limit is equivalent to  ), and we define
), and we define  .
.
Let  be a
be a  -dimensional array of real numbers. We define
-dimensional array of real numbers. We define  to be the
to be the  th-order finite difference of the
th-order finite difference of the  's at the point
's at the point  . Thus,
. Thus,  for all
for all  . For example, if
. For example, if  , then for all
, then for all  ,
,  (with the convention that
(with the convention that  ). We say that
). We say that  is a nondecreasing array if
is a nondecreasing array if  for any points
for any points  .
.
Hájek and Rényi [1] proved the following important inequality: If  is a sequence of (real-valued) independent random variables with zero means and finite second moments, and
is a sequence of (real-valued) independent random variables with zero means and finite second moments, and  is a nondecreasing sequence of positive real numbers, then for any
is a nondecreasing sequence of positive real numbers, then for any  and for any positive integers
and for any positive integers  ,
,

This inequality is a generalization of the Kolmogorov inequality and is a useful tool to prove the strong law of large numbers. Fazekas and Klesov [2] gave a general method for obtaining the strong law of large numbers for sequences of random variables by using a Hájek-Rényi-type maximal inequality. Afterwards, Noszály and Tómács [3] extended this result to multidimensional arrays (see also Klesov et al. [4]). They provided a sufficient condition for  -dimensional arrays of random variables to satisfy the strong law of large numbers
-dimensional arrays of random variables to satisfy the strong law of large numbers

where  is a positive, nondecreasing
is a positive, nondecreasing  -sequence of product type, that is,
-sequence of product type, that is,  , where
, where  is a nondecreasing sequence of positive real numbers for each
is a nondecreasing sequence of positive real numbers for each  . Then, we have
. Then, we have

This implies that

Therefore,


On the other hand, we can show that under the assumption that  is an array of positive real numbers satisfying (1.5), it is not possible to guarantee that (1.6) holds (for details, see Example 2.8 in the next section).
is an array of positive real numbers satisfying (1.5), it is not possible to guarantee that (1.6) holds (for details, see Example 2.8 in the next section).
Thus, if  is a positive, nondecreasing
is a positive, nondecreasing  -sequence of product type, then it is an array of positive real numbers satisfying (1.5), but the reverse is not true.
-sequence of product type, then it is an array of positive real numbers satisfying (1.5), but the reverse is not true.
In this paper, we use the hypothesis that  is an array of positive real numbers satisfying (1.5) and continue to study the problem of finding the sufficient condition for the strong law of large numbers (1.2). We also establish a Hájek-Rényi-type maximal inequality for multidimensional arrays of random elements and some maximal moment inequalities for arrays of dependent random elements.
is an array of positive real numbers satisfying (1.5) and continue to study the problem of finding the sufficient condition for the strong law of large numbers (1.2). We also establish a Hájek-Rényi-type maximal inequality for multidimensional arrays of random elements and some maximal moment inequalities for arrays of dependent random elements.
The paper is organized as follows. In the rest of this section, we recall some definitions and present some lemmas. Section 2 is devoted to our main results and their proofs.
Let  be a probability space. A family
be a probability space. A family  of nondecreasing sub-σ-algebras of
of nondecreasing sub-σ-algebras of  related to the partial order ⪯ on
related to the partial order ⪯ on  is said to be a stochastic basic.
is said to be a stochastic basic.
Let  be a stochastic basic such that
be a stochastic basic such that  if
if  , let
, let  be a real separable Banach space, let
be a real separable Banach space, let  be the
be the  -algebra of all Borel sets in
-algebra of all Borel sets in  , and let
, and let  be an array of random elements such that
be an array of random elements such that  is
is  -measurable for all
-measurable for all  . Then
. Then  is said to be an adapted array.
is said to be an adapted array.
For a given stochastic basic  , for
, for  , we set
, we set

in the case  , we set
, we set  .
.
An adapted array  is said to be a martingale difference array if
is said to be a martingale difference array if  for all
for all  and for all
and for all  .
.
In Quang and Huan [5], the authors showed that the set of all martingale difference arrays is really larger than the set of all arrays of independent mean zero random elements.
A Banach space  is said to be
is said to be  -uniformly smooth (
-uniformly smooth ( ) if
) if

A Banach space  is said to be
is said to be  -smoothable if there exists an equivalent norm under which
-smoothable if there exists an equivalent norm under which  is
is  -uniformly smooth.
-uniformly smooth.
Pisier [6] proved that a real separable Banach space  is
is  -smoothable (
-smoothable ( ) if and only if there exists a positive constant
) if and only if there exists a positive constant  such that for every
such that for every  integrable (
integrable ( -valued) martingale difference sequence
-valued) martingale difference sequence  ,
,

In Quang and Huan [5], this inequality was used to define  -uniformly smooth Banach spaces.
-uniformly smooth Banach spaces.
Let  be a sequence of independent identically distributed random variables with
be a sequence of independent identically distributed random variables with  . Let
. Let  and define
and define

Let  . Then,
. Then,  is said to be of Rademacher type
is said to be of Rademacher type if there exists a positive constant
if there exists a positive constant  such that
such that

It is well known that if a real separable Banach space is of Rademacher type 
 , then it is of Rademacher type
, then it is of Rademacher type  for all
for all  . Every real separable Banach space is of Rademacher type 1, while the
. Every real separable Banach space is of Rademacher type 1, while the  -spaces and
-spaces and  -spaces are of Rademacher type
-spaces are of Rademacher type  for
for  . The real line
. The real line  is of Rademacher type 2. Furthermore, if a Banach space is
is of Rademacher type 2. Furthermore, if a Banach space is  -smoothable, then it is of Rademacher type
-smoothable, then it is of Rademacher type  . For more details, the reader may refer to Borovskikh and Korolyuk [7], Pisier [8], and Woyczyński [9].
. For more details, the reader may refer to Borovskikh and Korolyuk [7], Pisier [8], and Woyczyński [9].
Now, we present some lemmas which will be needed in what follows. The first lemma is a variation of Lemma 2.6 of Fazekas and Tómács [10] and is a multidimensional version of the Kronecker lemma.
Lemma 1.1.
Let  be an array of nonnegative real numbers, and let
be an array of nonnegative real numbers, and let  be a nondecreasing array of positive real numbers such that
be a nondecreasing array of positive real numbers such that  as
as  . If
. If

then

Proof.
For every  , there exists a point
, there exists a point  such that
such that

Therefore, for all  ,
,

It means that

On the other hand, since  as
as  ,
,

Combining the above arguments, this completes the proof of Lemma 1.1.
The proof of the next lemma is very simple and is therefore omitted.
Lemma 1.2.
Let  be a probability space, and let
be a probability space, and let  be an array of sets in
be an array of sets in  such that
such that  for any points
for any points  . Then,
. Then,

Lemma 1.3.
Let  be an array of random elements. If for any
be an array of random elements. If for any  ,
,

then  .
.
Proof.
For each  , we have
, we have

Set

Then,  and for all
and for all  , for any
, for any  , there exists a point
, there exists a point  such that
such that  for all
for all  . It means that
. It means that

The proof is completed.
Lemma 1.4 (Quang and Huan [5]).
Let  , and let
, and let  be a real separable Banach space. Then, the following two statements are equivalent.
be a real separable Banach space. Then, the following two statements are equivalent.
(i)The Banach space  is
is  -smoothable.
-smoothable.
(ii)For every  integrable martingale difference array
integrable martingale difference array  , there exists a positive constant
, there exists a positive constant  (depending only on
(depending only on  and
and  ) such that
) such that

2. Main Results
Theorem 2.1 provides a Hájek-Rényi-type maximal inequality for multidimensional arrays of random elements. This theorem is inspired by the work of Shorack and Smythe [11].
Theorem 2.1.
Let  , let
, let  be an array of positive real numbers satisfying (1.5), and let
be an array of positive real numbers satisfying (1.5), and let  be an array of random elements in a real separable Banach space. Then, there exists a positive constant
be an array of random elements in a real separable Banach space. Then, there exists a positive constant  such that for any
such that for any  and for any points
and for any points  ,
,

Proof.
Since  is a nondecreasing array of positive real numbers,
is a nondecreasing array of positive real numbers,

For  , set
, set

Then, by interchanging the order of summation, we obtain the following

Thus, since  ,
,

By (2.2) and (2.5) and the Markov inequality, we have

This completes the proof of the theorem.
Now, we use Theorem 2.1 to prove a strong law of large numbers for multidimensional arrays of random elements. This result is inspired by Theorem 3.2 of Klesov et al. [4].
Theorem 2.2.
Let  , let
, let  be an array of nonnegative real numbers, let
be an array of nonnegative real numbers, let  be an array of positive real numbers satisfying (1.5) and
be an array of positive real numbers satisfying (1.5) and  as
as  , and let
, and let  be an array of random elements in a real separable Banach space such that for any points
be an array of random elements in a real separable Banach space such that for any points  ,
,

Then, the condition

implies (1.2).
Proof.
By (2.7) and Theorem 2.1, for any  and for any points
and for any points  , we have
, we have

This implies, by letting  , that
, that

Letting  , by (2.8) and Lemma 1.1, we obtain
, by (2.8) and Lemma 1.1, we obtain

Lemma 1.3 ensures that (1.2) holds. The proof is completed.
The next theorem provides three characterizations of  -smoothable Banach spaces. The equivalence of (i) and (ii) is an improvement of a result of Quang and Huan [5] (stated as Lemma 1.4 above).
-smoothable Banach spaces. The equivalence of (i) and (ii) is an improvement of a result of Quang and Huan [5] (stated as Lemma 1.4 above).
Theorem 2.3.
Let  , and let
, and let  be a real separable Banach space. Then, the following four statements are equivalent.
be a real separable Banach space. Then, the following four statements are equivalent.
(i)The Banach space  is
is  -smoothable.
-smoothable.
(ii)For every  integrable martingale difference array
integrable martingale difference array  , there exists a positive constant
, there exists a positive constant  such that
such that

(iii)For every  integrable martingale difference array
integrable martingale difference array  , for every array of positive real numbers
, for every array of positive real numbers  satisfying (1.5), for any
satisfying (1.5), for any  , and for any points
, and for any points  , there exists a positive constant
, there exists a positive constant  such that
such that

(iv)For every martingale difference array  , for every array of positive real numbers
, for every array of positive real numbers  satisfying (1.5) and
satisfying (1.5) and  as
as  , the condition
, the condition

implies (1.2).
Proof.
(i)⇒(ii): We easily obtain (2.12) in the case  . Now, we consider the case
. Now, we consider the case  . By virtue of Lemma 1.4, it suffices to show that
. By virtue of Lemma 1.4, it suffices to show that

First, we remark that for  , (2.15) follows from Doob's inequality. We assume that (2.15) holds for
, (2.15) follows from Doob's inequality. We assume that (2.15) holds for  , we wish to show that it holds for
, we wish to show that it holds for  .
.
For  , we set
, we set

Then,

Therefore,

It means that  is a nonnegative submartingale. Applying Doob's inequality, we obtain
is a nonnegative submartingale. Applying Doob's inequality, we obtain

We set

Then we again have that  is a martingale difference array. Therefore, by the inductive assumption, we obtain
is a martingale difference array. Therefore, by the inductive assumption, we obtain

Combining (2.19) and (2.21) yields that (2.15) holds for  .
.
-
(ii)
⇒ (iii): let
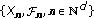 be an arbitrary
be an arbitrary  integrable martingale difference array. Then, for all
integrable martingale difference array. Then, for all 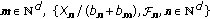 is also an
is also an  integrable martingale difference array. Therefore, the assertion (ii) and Theorem 2.1 ensure that (2.13) holds.
integrable martingale difference array. Therefore, the assertion (ii) and Theorem 2.1 ensure that (2.13) holds. -
(iii)
⇒ (iv): the proof of this implication is similar to the proof of Theorem 2.2 and is therefore omitted.
-
(iv)
⇒ (i): for a given positive integer
 , assume that (iv) holds. Let
, assume that (iv) holds. Let  be an arbitrary martingale difference sequence such that
be an arbitrary martingale difference sequence such that 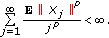 (2.22)
(2.22)
For  , set
, set

Then,  is a martingale difference array, and
is a martingale difference array, and  is an array of positive real numbers satisfying (1.5) and
is an array of positive real numbers satisfying (1.5) and  as
as  . Moreover, we see that
. Moreover, we see that

and so (1.2) holds. It means that

Then, by Theorem 2.2 of Hoffmann-Jørgensen and Pisier [12],  is
is  -smoothable.
-smoothable.
Remark 2.4.
The inequality (2.15) holds for every  and for every martingale difference array without imposing any geometric condition on the Banach space.
and for every martingale difference array without imposing any geometric condition on the Banach space.
In the case  , Theorem 2.3 reduces to the following corollary which was proved by Gan [13] and Gan and Qiu [14].
, Theorem 2.3 reduces to the following corollary which was proved by Gan [13] and Gan and Qiu [14].
Corollary 2.5.
Let  , and let
, and let  be a real separable Banach space. Then, the following three statements are equivalent.
be a real separable Banach space. Then, the following three statements are equivalent.
(i)The Banach space  is
is  -smoothable.
-smoothable.
(ii)For every  integrable martingale difference sequence
integrable martingale difference sequence  , for every nondecreasing sequence of positive real numbers
, for every nondecreasing sequence of positive real numbers  , for any
, for any  , and for any positive integers
, and for any positive integers  , there exists a positive constant
, there exists a positive constant  such that
such that

(iii)For every martingale difference sequence  and for every nondecreasing sequence of positive real numbers
and for every nondecreasing sequence of positive real numbers  such that
such that  as
as  , the condition
, the condition

implies

Remark 2.4 ensures that the inequality (2.15) holds for every  and for every array of independent mean zero random elements in a real separable Banach space. Therefore, by using the implication ((2.1.1) ⇒ (2.1.2)) of Theorem 2.1 of Hoffmann-Jørgensen and Pisier [12] and the same arguments as in the proof of Theorem 2.3, we get the following theorem which generalizes some results given by Christofides and Serfling [15] and Gan and Qiu [14]. We omit its proof.
and for every array of independent mean zero random elements in a real separable Banach space. Therefore, by using the implication ((2.1.1) ⇒ (2.1.2)) of Theorem 2.1 of Hoffmann-Jørgensen and Pisier [12] and the same arguments as in the proof of Theorem 2.3, we get the following theorem which generalizes some results given by Christofides and Serfling [15] and Gan and Qiu [14]. We omit its proof.
Theorem 2.6.
Let  , and let
, and let  be a real separable Banach space. Then, the following four statements are equivalent.
be a real separable Banach space. Then, the following four statements are equivalent.
(i)The Banach space  is of Rademacher type
is of Rademacher type  .
.
(ii)For every array of  integrable independent mean zero random elements
integrable independent mean zero random elements  , there exists a positive constant
, there exists a positive constant  such that (2.12) holds.
such that (2.12) holds.
(iii)For every array of  integrable independent mean zero random elements
integrable independent mean zero random elements  , for every array of positive real numbers
, for every array of positive real numbers  satisfying (1.5), for any
satisfying (1.5), for any  , and for any points
, and for any points  , there exists a positive constant
, there exists a positive constant  such that (2.13) holds.
such that (2.13) holds.
(iv)For every array of independent mean zero random elements  , for every array of positive real numbers
, for every array of positive real numbers  satisfying (1.5) and
satisfying (1.5) and  as
as  , the condition (2.14) implies (1.2).
, the condition (2.14) implies (1.2).
We close this paper by giving a remark on Theorem 2.6 and an example which illustrates Theorems 2.2, 2.3, and 2.6.
Remark 2.7.
By the same method as in the proof of Lemma 3 of Móricz et al. [16] and the same arguments as in the proof of Theorem 2.3, we can extend Theorem 2.6 to  -dependent random fields.
-dependent random fields.
Example 2.8.
Let  be a positive integer
be a positive integer  , and let
, and let  be an array of independent random variables with
be an array of independent random variables with

Then,  is an array of independent mean zero random variables taking values in the 2-smoothable Banach space
is an array of independent mean zero random variables taking values in the 2-smoothable Banach space  (using the absolute value as norm).
(using the absolute value as norm).
Let  . Then,
. Then,

It means that  is an array of positive real numbers satisfying (1.5) and
is an array of positive real numbers satisfying (1.5) and  as
as  . Moreover, by virtue of (1.6), we can show that
. Moreover, by virtue of (1.6), we can show that  is not a positive, nondecreasing
is not a positive, nondecreasing  -sequence of product type. Therefore, (1.2) does not follow from Theorem 3.2 of Klesov et al. [4]. But for every array of positive real numbers
-sequence of product type. Therefore, (1.2) does not follow from Theorem 3.2 of Klesov et al. [4]. But for every array of positive real numbers  ,
,  is a martingale difference array such that
is a martingale difference array such that

and so (2.7) and (2.8) are satisfied, Theorem 2.2 ensures that (1.2) holds.
As we know, the limit  is equivalent to
is equivalent to  . Recently, some authors have derived the sufficient conditions for the strong law of large numbers
. Recently, some authors have derived the sufficient conditions for the strong law of large numbers

where  is one of the special kinds of positive, nondecreasing
is one of the special kinds of positive, nondecreasing  -sequences of product type. For more details, the reader may refer to [17–19]. Therefore, this example also shows that the implications ((i) ⇒ (iv)) of Theorem 2.3 and ((i) ⇒ (iv)) of Theorem 2.6 are independent of results obtained in [17–19].
-sequences of product type. For more details, the reader may refer to [17–19]. Therefore, this example also shows that the implications ((i) ⇒ (iv)) of Theorem 2.3 and ((i) ⇒ (iv)) of Theorem 2.6 are independent of results obtained in [17–19].
References
Hájek J, Rényi A: Generalization of an inequality of Kolmogorov. Acta Mathematica Academiae Scientiarum Hungaricae 1955, 6: 281–283. 10.1007/BF02024392
Fazekas I, Klesov O: A general approach to the strong laws of large numbers. Theory of Probability and Its Applications 2002, 45(3):436–449.
Noszály C, Tómács T: A general approach to strong laws of large numbers for fields of random variables. Annales Universitatis Scientiarum Budapestinensis de Rolando Eötvös Nominatae. Sectio Mathematica 2001, 43: 61–78.
Klesov O, Fazekas I, Noszály C, Tómács T: Strong laws of large numbers for sequences and fields. Theory of Stochastic Processes 2008, 5(3–4):91–104.
Quang NV, Huan NV: A characterization of p -uniformly smooth Banach spaces and weak laws of large numbers for d -dimensional adapted arrays. The Indian Journal of Statistics 2010, 72: 344–358. 10.1007/s12262-010-0079-3
Pisier G: Martingales with values in uniformly convex spaces. Israel Journal of Mathematics 1975, 20(3–4):326–350. 10.1007/BF02760337
Borovskikh YV, Korolyuk VS: Martingale Approximation. VSP, Utrecht, The Netherlands; 1997:xii+322.
Pisier G: Probabilistic methods in the geometry of Banach spaces. In Probability and Analysis (Varenna, 1985), Lecture Notes in Mathematics. Volume 1206. Springer, Berlin, Germany; 1986:167–241.
Woyczyński WA: On Marcinkiewicz-Zygmund laws of large numbers in Banach spaces and related rates of convergence. Probability and Mathematical Statistics 1981, 1(2):117–131.
Fazekas I, Tómács T: Strong laws of large numbers for pairwise independent random variables with multidimensional indices. Publicationes Mathematicae Debrecen 1998, 53(1–2):149–161.
Shorack GR, Smythe RT: Inequalities for where . Proceedings of the American Mathematical Society 1976, 54: 331–336.
Hoffmann-Jørgensen J, Pisier G: The law of large numbers and the central limit theorem in Banach spaces. Annals of Probability 1976, 4(4):587–599. 10.1214/aop/1176996029
Gan S: The Hàjek-Rènyi inequality for Banach space valued martingales and the p smoothness of Banach spaces. Statistics & Probability Letters 1997, 32(3):245–248. 10.1016/S0167-7152(96)00080-6
Gan S, Qiu D: On the Hájek-Rényi inequality. Wuhan University Journal of Natural Sciences 2007, 12(6):971–974. 10.1007/s11859-007-0029-5
Christofides TC, Serfling RJ: Maximal inequalities for multidimensionally indexed submartingale arrays. The Annals of Probability 1990, 18(2):630–641. 10.1214/aop/1176990849
Móricz F, Stadtmüller U, Thalmaier M: Strong laws for blockwise ℳ -dependent random fields. Journal of Theoretical Probability 2008, 21(3):660–671. 10.1007/s10959-007-0127-5
Dung LV, Ngamkham T, Tien ND, Volodin AI: Marcinkiewicz-Zygmund type law of large numbers for double arrays of random elements in Banach spaces. Lobachevskii Journal of Mathematics 2009, 30(4):337–346. 10.1134/S1995080209040118
Quang NV, Huan NV: On the strong law of large numbers and ℒp-convergence for double arrays of random elements in p -uniformly smooth Banach spaces. Statistics & Probability Letters 2009, 79(18):1891–1899. 10.1016/j.spl.2009.05.014
Thanh LV: On the strong law of large numbers for d -dimensional arrays of random variables. Electronic Communications in Probability 2007, 12: 434–441.
Acknowledgments
The authors are grateful to the referee for carefully reading the paper and for offering some comments which helped to improve the paper. This research was supported by the National Foundation for Science Technology Development, Vietnam (NAFOSTED), no. 101.02.32.09.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Quang, N., Van Huan, N. A Hájek-Rényi-Type Maximal Inequality and Strong Laws of Large Numbers for Multidimensional Arrays. J Inequal Appl 2010, 569759 (2010). https://doi.org/10.1155/2010/569759
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/569759
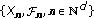 be an arbitrary
be an arbitrary  integrable martingale difference array. Then, for all
integrable martingale difference array. Then, for all 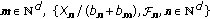 is also an
is also an  integrable martingale difference array. Therefore, the assertion (ii) and Theorem 2.1 ensure that (2.13) holds.
integrable martingale difference array. Therefore, the assertion (ii) and Theorem 2.1 ensure that (2.13) holds. , assume that (iv) holds. Let
, assume that (iv) holds. Let  be an arbitrary martingale difference sequence such that
be an arbitrary martingale difference sequence such that