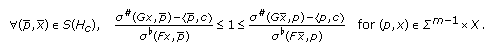- Research Article
- Open access
- Published:
Solvability Criteria for Some Set-Valued Inequality Systems
Journal of Inequalities and Applications volume 2010, Article number: 543061 (2010)
Abstract
Arising from studying some multivalued von Neumann model, three set-valued inequality systems are introduced, and two solvability questions are considered. By constructing some auxiliary functions and studying their minimax and saddle-point properties, solvability criteria composed of necessary and sufficient conditions regarding these inequality systems are obtained.
1. Introduction
Arising from considering some multivalued von Neumann model, this paper aims to study three set-valued inequality systems and try to find their solvability criteria. Before starting with this subject, we need to review some necessary backgrounds as follows.
We denote by  the
the  -dimensional Euclidean space,
-dimensional Euclidean space,  its dual, and
its dual, and  the duality pairing on
the duality pairing on  ; moreover, we denote that
; moreover, we denote that  and int
and int  is its interior. We also define
is its interior. We also define  (or
(or  ) in
) in  by
by  (or by
(or by  int
int  ).
).
It is known that the generalized (linear or nonlinear) von Neumann model, which is composed of an inequality system and a growth factor problem described by

is one of the most important issues in the input-output analysis [1–3], where  ,
,  (
( may not be equal to
may not be equal to  ), and
), and  are two nonnegative or positive maps from
are two nonnegative or positive maps from  to
to  . A series of researches on (1.1) have been made by the authors of [1–5] for the linear case (i.e.,
. A series of researches on (1.1) have been made by the authors of [1–5] for the linear case (i.e.,  are
are  matrices) and by the authors of [6, 7] for the nonlinear case (i.e.,
matrices) and by the authors of [6, 7] for the nonlinear case (i.e.,  are some types of nonlinear maps). Since (a) or (b) of (1.1) is precisely a special example of the inequality
are some types of nonlinear maps). Since (a) or (b) of (1.1) is precisely a special example of the inequality  if we restrict
if we restrict  or
or  , it is enough for (1.1) to consider the inequality system. This idea can be extended to the set-valued version. Indeed, if
, it is enough for (1.1) to consider the inequality system. This idea can be extended to the set-valued version. Indeed, if  and
and  are replaced by set-valued maps
are replaced by set-valued maps  and
and  , respectively, then (1.1) yields a class of multivalued von Neumann model, and it solves a proper set-valued inequality system to study. With this idea, by [8] (as a set-valued extension to [6, 7]) we have considered the following multivalued inequality system:
, respectively, then (1.1) yields a class of multivalued von Neumann model, and it solves a proper set-valued inequality system to study. With this idea, by [8] (as a set-valued extension to [6, 7]) we have considered the following multivalued inequality system:

and obtained several necessary and sufficient conditions for its solvability, where  and
and  is a class of set-valued maps from
is a class of set-valued maps from  to
to  . Along the way, three further set-valued inequality systems that we will study in the sequel can be stated as follows.
. Along the way, three further set-valued inequality systems that we will study in the sequel can be stated as follows.
Let  ,
,  be as above, and let
be as above, and let  be set-valued maps from
be set-valued maps from  to
to  , then we try to find the solvability criteria (i.e., the necessary and sufficient conditions) that
, then we try to find the solvability criteria (i.e., the necessary and sufficient conditions) that  solves
solves



When  and
and  are single-valued maps, then (1.3)–(1.5) return to the models of [6, 7]. When
are single-valued maps, then (1.3)–(1.5) return to the models of [6, 7]. When  and
and  ,
,  are set-valued maps, there are three troubles if we try to obtain some meaningful solvability criteria regarding (1.3)–(1.5) just like what we did in [8].
are set-valued maps, there are three troubles if we try to obtain some meaningful solvability criteria regarding (1.3)–(1.5) just like what we did in [8].
-
(1)
For (1.2) and (1.3), it is possible that only (1.2) has solution for some
 . Indeed, if
. Indeed, if  is compact and
is compact and 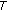 is continuous, compact valued with
is continuous, compact valued with 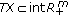 , then
, then 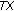 is compact and there is
is compact and there is  with
with 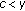 for
for 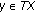 . Hence
. Hence  solves (1.2) but does not solve (1.3).
solves (1.2) but does not solve (1.3). -
(2)
It seems that the solvability criteria (namely, necessary and sufficient results concerning existence) to (1.4) can be obtained immediately by [8] with the replacement
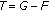 . However, this type of result is trivial because it depends only on the property of
. However, this type of result is trivial because it depends only on the property of  but not on the respective information of
but not on the respective information of 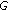 and
and 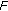 . This opinion is also applicable to (1.3) and (1.5).
. This opinion is also applicable to (1.3) and (1.5). -
(3)
Clearly, (1.3) (or (1.5)) is more fine and more useful than (1.2) (or (1.4)). However, the method used for
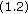 in [8] (or the possible idea for (1.4)) to obtain solvability criteria fails to be applied to find the similar characteristic results for (1.3) (or (1.5)) because there are some examples (see Examples 3.5 and 4.4) to show that, without any additional restrictions, no necessary and sufficient conditions concerning existence for them can be obtained. This is also a main cause that the author did not consider
in [8] (or the possible idea for (1.4)) to obtain solvability criteria fails to be applied to find the similar characteristic results for (1.3) (or (1.5)) because there are some examples (see Examples 3.5 and 4.4) to show that, without any additional restrictions, no necessary and sufficient conditions concerning existence for them can be obtained. This is also a main cause that the author did not consider 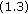 and
and 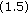 in [8].
in [8].
So some new methods should be introduced if we want to search out the solvability criteria to (1.3)–(1.5). In the sections below, we are devoted to study (1.3)–(1.5) by considering two questions under two assumptions as follows:
Question 1.
Whether there exist any criteria that  solves (1.3) in some proper way?
solves (1.3) in some proper way?
Question 2.
Like Question 1, whether there exist any solvability criteria to (1.4) or (1.5) that depend on the respective information of  and
and  ?
?
Assumption.
 is a fixed point and
is a fixed point and  is a convex compact subset.
is a convex compact subset.
Assumption.
Consider the following: 
 and
and  are upper semicontinuous and convex set-valued maps with nonempty convex compact values.
are upper semicontinuous and convex set-valued maps with nonempty convex compact values.
By constructing some functions and studying their minimax properties, some progress concerning both questions has been made. The paper is arranged as follows. We review some concepts and known results in Section 2 and prove three Theorems composed of necessary and sufficient conditions regarding the solvability of (1.3)–(1.5) in Sections 3 and 4. Then we present the conclusion in Section 5.
2. Terminology
Let  ,
,  , and
, and  (
( ). Let
). Let  ,
,  , and
, and  be functions and
be functions and  a set-valued map. We need some concepts concerning
a set-valued map. We need some concepts concerning  ,
,  and
and  and
and  such as convex or concave and upper or lower semicontinuous (in short, u.s.c. or l.s.c.) and continuous (i.e., both u.s.c. and l.s.c.), whose definitions can be found in [9–11], therefore, the details are omitted here. We also need some further concepts to
such as convex or concave and upper or lower semicontinuous (in short, u.s.c. or l.s.c.) and continuous (i.e., both u.s.c. and l.s.c.), whose definitions can be found in [9–11], therefore, the details are omitted here. We also need some further concepts to  ,
,  , and
, and  as follows.
as follows.
Definition 2.1.
(1) is said to be closed if its graph defined by graph
is said to be closed if its graph defined by graph  is closed in
is closed in  . Moreover,
. Moreover,  is said to be upper semicontinuous (in short, u.s.c.) if, for each
is said to be upper semicontinuous (in short, u.s.c.) if, for each  and each neighborhood
and each neighborhood  of
of  , there exists a neighborhood
, there exists a neighborhood  of
of  such that
such that  .
.
-
(2)
Assume that
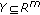 (
(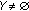 ), and define
), and define 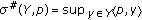 ,
, 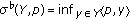 (
(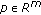 ). Then
). Then 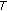 is said to be upper hemicontinuous (in short, u.h.c.) if
is said to be upper hemicontinuous (in short, u.h.c.) if 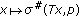 is u.s.c. on
is u.s.c. on  for any
for any 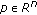 .
.
(3) is said to be convex if
is said to be convex if  is convex and
is convex and  for any
for any  and
and  .
.
(4)
(a)If  , then one claims that the minimax equality of
, then one claims that the minimax equality of  holds. Denoting by
holds. Denoting by  the value of the preceding equality, one also says that the minimax value
the value of the preceding equality, one also says that the minimax value  of
of  exists. If
exists. If  such that
such that  , then one calls
, then one calls  a saddle point of
a saddle point of  . Denote by
. Denote by  the set of all saddle points of
the set of all saddle points of  (i.e.,
(i.e.,  ), and define
), and define  , the restriction of
, the restriction of  to
to  if
if  is nonempty.
is nonempty.
(b)Replacing  by
by  and
and  by
by  , with the similar method one can also define
, with the similar method one can also define  (the minimax value of
(the minimax value of  ),
),  (the saddle-point set of
(the saddle-point set of  ), and
), and  (the restriction of
(the restriction of  to
to  ).
).
-
(5)
If
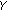 is a convex set and
is a convex set and  a subset of
a subset of  , one claims that
, one claims that 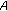 is an extremal subset of
is an extremal subset of 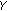 if
if 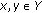 and
and 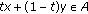 for some
for some 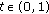 entails
entails  .
.  is an extremal point of
is an extremal point of 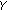 if
if 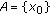 is an extremal subset of
is an extremal subset of 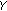 , and the set of all extremal points of
, and the set of all extremal points of  is denoted by ext
is denoted by ext 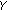 .
.
Remark 2.2.
-
(1)
Since
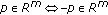 and
and 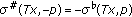 , we can see that
, we can see that 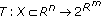 is u.h.c. if and only if
is u.h.c. if and only if  is l.s.c. on
is l.s.c. on 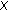 for any
for any 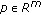 .
. -
(2)
For the function
 on
on 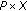 ,
, 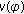 exists if and only if
exists if and only if  , and
, and 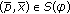 if and only if
if and only if 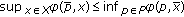 if and only if
if and only if  for any
for any 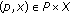 . If
. If 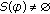 , then
, then 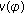 exists, and
exists, and 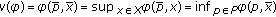 for any
for any  . The same properties are also true for
. The same properties are also true for 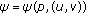 on
on  . Moreover, we have
. Moreover, we have 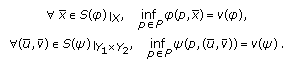 (2.1)
(2.1)
We also need three known results as follows.
Lemma 2.3.
-
(1)
(see [9]) If
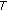 is u.s.c., then
is u.s.c., then 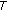 is u.h.c.
is u.h.c.
-
(2)
(see [9]) If
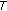 is u.s.c. with closed values, then
is u.s.c. with closed values, then  is closed.
is closed. -
(3)
(see [9]) If
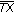 (the closure of
(the closure of 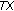 ) is compact and
) is compact and 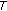 is closed, then
is closed, then 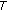 is u.s.c.
is u.s.c. -
(4)
If
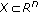 is compact and
is compact and  is u.s.c. with compact values, then
is u.s.c. with compact values, then 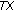 is compact in
is compact in 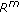 .
. -
(5)
If
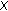 is convex (or compact) and
is convex (or compact) and  are convex (or u.s.c. with compact values), then
are convex (or u.s.c. with compact values), then 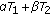 are also convex (or u.s.c.) for all
are also convex (or u.s.c.) for all 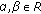 .
.
Proof.
We only need to prove (5).
-
(a)
If
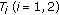 are convex,
are convex, 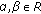 ,
, 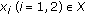 , and
, and 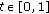 , then
, then 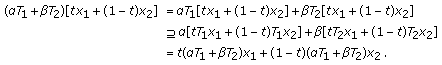 (2.2)
(2.2)
Hence  is convex.
is convex.
-
(b)
Now we assume that
 is compact.
is compact.
In case  is u.s.c. with compact values and
is u.s.c. with compact values and  , then by (2), (4),
, then by (2), (4),  is closed and the range
is closed and the range  of
of  is compact. If
is compact. If  , then
, then  for any
for any  ; hence,
; hence,  is u.s.c. If
is u.s.c. If  , supposing that
, supposing that  graph
graph with
with  , then
, then  graph
graph  such that
such that  as
as  , which implies that
, which implies that  . Hence,
. Hence,  is closed and also u.s.c. because of (3).
is closed and also u.s.c. because of (3).
In case  are u.s.c. with compact values, if
are u.s.c. with compact values, if graph
graph with
with  , then
, then  and there exist
and there exist  ,
,  such that
such that  for all
for all  By (4),
By (4),  and
and  are compact, so we can suppose
are compact, so we can suppose  and
and  as
as  . By (2), both
. By (2), both  are closed, this implies that
are closed, this implies that  , and thus
, and thus  is closed. Hence by (3),
is closed. Hence by (3),  is u.s.c. because
is u.s.c. because  and
and  is compact.
is compact.
Lemma 2.4 (see [8, Theorems  and
and  ]).
]).
Let  be convex compact with
be convex compact with  ,
,  , and
, and  . Assume that
. Assume that  is convex and u.s.c. with nonempty convex compact values, and define
is convex and u.s.c. with nonempty convex compact values, and define  on
on  by
by  for
for  . Then
. Then
(1) exists and
exists and  is a convex compact subset of
is a convex compact subset of  ,
,
(2) solves (1.2)
solves (1.2)  for
for  .
.
In particular, both (1) and (2) are also true if  .
.
Lemma 2.5.
-
(1)
(see [10, 11]) If
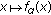 is convex or l.s.c. (resp., concave or u.s.c.) on
is convex or l.s.c. (resp., concave or u.s.c.) on 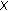 for
for 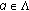 and
and 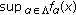 (resp.,
(resp.,  ) is finite for
) is finite for 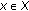 , then
, then 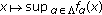 (resp.,
(resp., 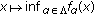 ) is also convex or l.s.c. (resp., concave or u.s.c.) on
) is also convex or l.s.c. (resp., concave or u.s.c.) on  .
. -
(2)
(see [11]) If
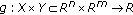 is l.s.c. (or u.s.c.) and
is l.s.c. (or u.s.c.) and 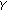 is compact, then
is compact, then 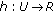 defined by
defined by  (or
(or  defined by
defined by 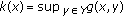 ) is also l.s.c. (or u.s.c.).
) is also l.s.c. (or u.s.c.). -
(3)
(see [9–11], Minimax Theorem) Let
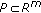 ,
, 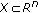 be convex compact, and let
be convex compact, and let 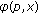 be defined on
be defined on 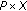 . If, for each
. If, for each 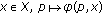 is convex and l.s.c. and, for each
is convex and l.s.c. and, for each 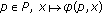 is concave and u.s.c., then
is concave and u.s.c., then 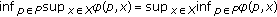 and there exists
and there exists 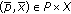 such that
such that 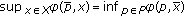 .
.
3. Solvability Theorem to (1.3)
Let  be introduced as in Lemma 2.4, and define the functions
be introduced as in Lemma 2.4, and define the functions  on
on  and
and  on
on  by
by

Remark 3.1.
By both Assumptions in Section 1, Definition 2.1, and Lemmas 2.4 and 2.5, we can see that
(1) for all
for all  ,
,
(2) and
and  exist, and
exist, and  and
and  are nonempty,
are nonempty,
(3) solves (1.2) if and only if
solves (1.2) if and only if  if and only if
if and only if  with
with  .
.
Hence,  and
and  are nonempty. Moreover, we have the following.
are nonempty. Moreover, we have the following.
Theorem 3.2.
For (1.3), the following three statements are equivalent to each other:
(1) ,
,
(2)for all  , for all
, for all  ,
,  ,
,  ,
,
(3) ,
,  ,
,  ,
,  .
.
Remark 3.3.
Clearly, each of (2) and (3) implies that  solves (1.3) because
solves (1.3) because  and
and  . So we conclude from Theorem 3.2 that
. So we conclude from Theorem 3.2 that  solves (1.3) in the way of (2) or in the way of (3) if and only if
solves (1.3) in the way of (2) or in the way of (3) if and only if  .
.
Proof of Theorem 3.2.
We only need to prove (1) (2) and (3)
(2) and (3) (1).
(1).
(1) (2). Assume that (1) holds. By (3.1) and Remarks 2.2 and 3.1, it is easy to see that
(2). Assume that (1) holds. By (3.1) and Remarks 2.2 and 3.1, it is easy to see that

Then for each  and each
and each  , we have
, we have

By taking  , it follows that
, it follows that  . Hence,
. Hence,  . On the other hand, it is easy to verify that
. On the other hand, it is easy to verify that  is a nonempty extremal subset of
is a nonempty extremal subset of  . The Crain-Milmann Theorem (see [12]) shows that ext
. The Crain-Milmann Theorem (see [12]) shows that ext  is nonempty with ext
is nonempty with ext  ext
ext  . So there exists
. So there exists  such that
such that  ext
ext  . This implies by (3.3) that
. This implies by (3.3) that  , and therefore (2) follows.
, and therefore (2) follows.
(3) (1). Let
(1). Let  ,
,  , and let
, and let  be presented in (3). Since
be presented in (3). Since  solves (1.3) and also solves (1.2), by (3.1) and Remarks 2.2 and 3.1, we obtain
solves (1.3) and also solves (1.2), by (3.1) and Remarks 2.2 and 3.1, we obtain

where  . Hence,
. Hence,  and the theorem follows.
and the theorem follows.

Remark 3.4.
From the Theorem, we know that  implies that
implies that  solves (1.3). However, without any additional restricting conditions, the inverse may not be true.
solves (1.3). However, without any additional restricting conditions, the inverse may not be true.
Example 3.5.
Let  , and let
, and let  be defined by
be defined by  for
for  Then
Then  is an u.s.c. and convex set-valued map with convex compact values, and for each
is an u.s.c. and convex set-valued map with convex compact values, and for each  ,
,  and
and  ,
,  . Hence,
. Hence,  for all
for all  and therefore,
and therefore,

This implies that  (or
(or  ) may not be the necessary (or the sufficient) condition that
) may not be the necessary (or the sufficient) condition that  solves (1.3).
solves (1.3).
4. Solvability Theorems to (1.4) and (1.5)
Taking  , then from both Assumptions, Lemma 2.4, and Theorem 3.2, we immediately obtain the necessary and sufficient conditions to the solvability of (1.4) and (1.5). However, just as indicated in Section 1, this type of result is only concerned with
, then from both Assumptions, Lemma 2.4, and Theorem 3.2, we immediately obtain the necessary and sufficient conditions to the solvability of (1.4) and (1.5). However, just as indicated in Section 1, this type of result is only concerned with  . To get some further solvability criteria to (1.4) and (1.5) depending on the respective information of
. To get some further solvability criteria to (1.4) and (1.5) depending on the respective information of  and
and  , we define the functions
, we define the functions  on
on  and
and  on
on  by
by

By both Assumptions, we know that  and
and  are finite with
are finite with  and
and  for
for  and
and  , so the functions
, so the functions  and
and  defined by (4.1) are well defined.
defined by (4.1) are well defined.
In view of Definition 2.1, we denote by  (or
(or  ) the minimax value of
) the minimax value of  (or
(or  ) if it exists,
) if it exists,  (or
(or  ) the saddle point set if it is nonempty, and
) the saddle point set if it is nonempty, and  (or
(or  ) the restriction of
) the restriction of  to
to  (or
(or  to
to  ). Then we have the solvability result to (1.4) and (1.5) as follows.
). Then we have the solvability result to (1.4) and (1.5) as follows.
Theorem 4.1.
(i) exists if and only if
exists if and only if  .
.
(ii)
(1) solves (1.4) if and only if
solves (1.4) if and only if  exists with
exists with  if and only if
if and only if  with
with  for
for  .
.
(2)In particular, if  exists with
exists with  , then for each
, then for each  , there exists
, there exists  such that
such that 
Theorem 4.2.
For (1.5), the following three statements are equivalent to each other:
(1) ,
,
(2) ,
,  , and for all
, and for all  , for all
, for all  ,
,  ,
,  ,
,
(3) ,
,  , and
, and  ,
,  ,
,  ,
, 
That is,  solves (1.5) in the way of (2) or in the way of (3) if and only if
solves (1.5) in the way of (2) or in the way of (3) if and only if  .
.
Remark 4.3.
It is also needed to point out that  is not the necessary condition of
is not the necessary condition of  making (1.5) solvable without any other restricting conditions.
making (1.5) solvable without any other restricting conditions.
Example 4.4.
Let  ,
,  , and
, and  be defined by
be defined by  ,
,  for
for  Then both
Then both  and
and  are u.s.c. convex set-valued maps with convex compact values, and for any
are u.s.c. convex set-valued maps with convex compact values, and for any  ,
,  , and
, and  , we have
, we have  ,
,  ,
,  , and
, and  Therefore,
Therefore,

This implies that, for each  ,
,  solves (1.5) but
solves (1.5) but  .
.
The proof of both Theorems 4.1 and 4.2 can be divided into eight lemmas.
Let  ,
,  , and
, and  . Consider the auxiliary inequality system
. Consider the auxiliary inequality system

Then  solves (4.3) if and only if
solves (4.3) if and only if  solves (1.2) for
solves (1.2) for  , and in particular,
, and in particular,  solves (4.3) if and only if
solves (4.3) if and only if  solves (1.4). Define
solves (1.4). Define  on
on  by
by

denote by  the minimax value of
the minimax value of  if it exists, and denote by
if it exists, and denote by  the saddle point set if it is nonempty. Then we have the following.
the saddle point set if it is nonempty. Then we have the following.
Lemma 4.5.
-
(1)
For each
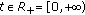 ,
,  exists and
exists and 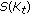 is nonempty. Moreover,
is nonempty. Moreover,  solves (4.3) if and only if
solves (4.3) if and only if 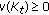 if and only if
if and only if 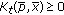 for
for 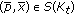 .
. -
(2)
The function
 is continuous and strictly decreasing on
is continuous and strictly decreasing on 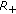 with
with  .
.
Proof.
-
(1)
By both Assumptions and Lemmas 2.3(4) and 2.3(5),
 is convex and u.s.c. with nonempty convex compact values for each
is convex and u.s.c. with nonempty convex compact values for each  . Since
. Since  for
for  , applying Lemma 2.4 to
, applying Lemma 2.4 to 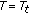 and substituting
and substituting  for
for 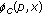 , we know that (1) is true.
, we know that (1) is true.
-
(2)
We prove (2) in three steps as follows.
(a)By Lemma 2.3(1),  and
and  are u.h.c., which implies by Definition 2.1(2) and Remark 2.2(1) that for each
are u.h.c., which implies by Definition 2.1(2) and Remark 2.2(1) that for each  ,
,  is u.s.c. on
is u.s.c. on  . Then from Lemma 2.5(1)(2), we know that both functions
. Then from Lemma 2.5(1)(2), we know that both functions

Since  and
and  are compact by both Assumptions and Lemma 2.3(4),
are compact by both Assumptions and Lemma 2.3(4),  and
and  are finite. Then for any
are finite. Then for any  ,
,  and
and  , we have
, we have

This implies that, for each  ,
,

Hence for each  ,
,  is continuous on
is continuous on  . Also from Lemmas 2.5(1) and 2.5(2), it follows that both functions
. Also from Lemmas 2.5(1) and 2.5(2), it follows that both functions

So we conclude from (4.5), (4.8), and Statement (1) that  is continuous on
is continuous on  .
.
(b)Assume that  . Since
. Since  int
int  is compact, it is easy to see that
is compact, it is easy to see that  . Thus for any
. Thus for any  , we have
, we have

which implies that  , and hence
, and hence  is strict decreasing on
is strict decreasing on  .
.
(c)Let  and
and  . By both Assumptions,
. By both Assumptions,  and
and  are finite. Thus for any
are finite. Thus for any  and
and  , we have
, we have

This implies that  . Therefore,
. Therefore,  . This completes the proof.
. This completes the proof.
Lemma 4.6.
(1) and
and  are l.s.c. on
are l.s.c. on  .
.
(2) ) and
) and  are u.s.c. on
are u.s.c. on  .
.
(3) exists if and only if
exists if and only if  is nonempty.
is nonempty.
Proof.
-
(1)
Since, for each
 and
and 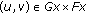 , the function
, the function 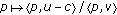 is continuous on
is continuous on  , from Lemma 2.5(1), we can see that
, from Lemma 2.5(1), we can see that 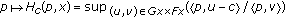
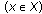 and
and 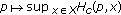 are l.s.c., hence (1) is true.
are l.s.c., hence (1) is true.
-
(2)
Assume that
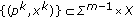 is a sequence with
is a sequence with 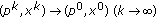 , then for each
, then for each  , there exist
, there exist  and
and  such that
such that 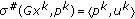 ,
, 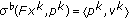 . Since
. Since 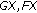 are compact and
are compact and 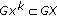 ,
, 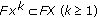 , we may choose
, we may choose  and
and  such that
such that  (4.11)
(4.11)
By Lemma 2.3(2), both  and
and  are closed. Hence,
are closed. Hence,  and
and  , which in turn imply that
, which in turn imply that  and
and

Combining this with  for
for  , it follows that
, it follows that

Hence by (4.1),  is u.s.c. on
is u.s.c. on  , so is
, so is  on
on  thanks to Lemma 2.5(1).
thanks to Lemma 2.5(1).
-
(3)
Assume that
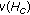 exists. By (1) and (2), there exist
exists. By (1) and (2), there exist 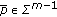 and
and  such that
such that

By Remark 2.2(2),  . Hence
. Hence  is nonempty. The inverse is obvious. This completes the proof.
is nonempty. The inverse is obvious. This completes the proof.
Lemma 4.7.
-
(1)
If
 solves(1.4), then
solves(1.4), then 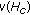 exists with
exists with  .
.
(2)If  exists with
exists with  , then
, then  and
and  for
for  .
.
Proof.
-
(1)
If
 solves (1.4), then
solves (1.4), then  solves (4.3). From Lemma 4.5, we know that
solves (4.3). From Lemma 4.5, we know that 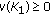 , and there is a unique
, and there is a unique 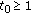 such that
such that 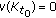 . Moreover, also from Lemma 4.5,
. Moreover, also from Lemma 4.5, 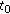 is the biggest number that makes (4.3) solvable, and thus
is the biggest number that makes (4.3) solvable, and thus  solves (4.3) if and only if
solves (4.3) if and only if  . We will prove that
. We will prove that 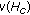 exists with
exists with  . Let
. Let 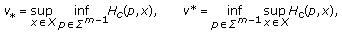 (4.15)
(4.15)
then  . It is needed to show that
. It is needed to show that  .
.
Since  solves (4.3), there exist
solves (4.3), there exist  ,
,  , and
, and  such that
such that  . Hence for each
. Hence for each  As
As  for
for  , it follows from (4.1) that
, it follows from (4.1) that  and thus
and thus

On the other hand, by (4.15), for each  we have
we have  . By (4.1) and Lemma 4.6(2), there exists
. By (4.1) and Lemma 4.6(2), there exists  such that
such that

It deduces from (4.4) that for each 

Hence by Lemma 4.5(1),  , and
, and  solves (4.3). Since
solves (4.3). Since  is the biggest number that makes (4.3) solvable, we have
is the biggest number that makes (4.3) solvable, we have  . Combining this with (4.16), we obtain
. Combining this with (4.16), we obtain  . Therefore,
. Therefore,  exists and
exists and 
-
(2)
follows immediately from Lemma 4.6(3) and Remark 2.2(2). The third lemma follows.
Lemma 4.8.
If  with
with  for
for  , then
, then  solves (1.4). Moreover, for each
solves (1.4). Moreover, for each  , there exists
, there exists  such that
such that 
Proof.
By (4.1) and Remark 2.2(2), we know that, for each  ,
,

Combining this with the definition of  (i.e., (4.4) for
(i.e., (4.4) for  ), it follows that, for each
), it follows that, for each  and each
and each  ,
,

Hence by Definition 2.1(4) and Remark 2.2(2),

It follows that  implies that
implies that  with
with  and so
and so

Applying Lemma 4.5(1) to  , we then conclude that
, we then conclude that  solves (4.3). So there exist
solves (4.3). So there exist  ,
,  , and
, and  such that
such that  . Hence
. Hence  solves (1.4) because
solves (1.4) because  ,
,  , and
, and  .
.
For each  . Since
. Since  by (4.4), applying Lemma 2.5(3) to the function
by (4.4), applying Lemma 2.5(3) to the function  on
on  and associating with (4.22), we obtain
and associating with (4.22), we obtain

Since  is u.s.c. on
is u.s.c. on  , from (4.23) there exist
, from (4.23) there exist  ,
,  such that
such that  satisfies
satisfies

By taking  , we get
, we get  , and therefore
, and therefore  satisfies
satisfies  because
because  . This completes the proof.
. This completes the proof.
Proof of Theorem 4.1.
By Lemmas 4.6(3), 4.7, and 4.8, we know that Theorem 4.1 is true.
To prove Theorem 4.2, besides using Lemmas 4.5–4.8, for  and
and  , we also need to study the condition that
, we also need to study the condition that  solves
solves

Define  on
on  by
by

We denote by  the minimax values of
the minimax values of  if it exists,
if it exists,  the saddle point set if it is nonempty, and
the saddle point set if it is nonempty, and  its restriction to
its restriction to  .
.
Lemma 4.9.
Let  and
and  be fixed. Then one has the following.
be fixed. Then one has the following.
(1)For each  exists and
exists and  is nonempty.
is nonempty.
(2) solves (4.25) if and only if
solves (4.25) if and only if  if and only if
if and only if  implies that
implies that 
(3) is continuous and strict decreasing on
is continuous and strict decreasing on  with
with 
Proof.
Define  from
from  to
to  by
by

Then  is a single-valued continuous map with the convex condition defined by Definition 2.1(3) because
is a single-valued continuous map with the convex condition defined by Definition 2.1(3) because  for all
for all  and
and  .
.
Since  is convex and compact in
is convex and compact in  , replacing
, replacing  by
by  ,
,  by
by  , and
, and  by
by  , from Lemma 2.4, we know that both (1) and (2) are true. Moreover, with the same method as in proving Lemma 4.5(2), we can show that (3) is also true. (In fact, since
, from Lemma 2.4, we know that both (1) and (2) are true. Moreover, with the same method as in proving Lemma 4.5(2), we can show that (3) is also true. (In fact, since  is continuous on
is continuous on  and
and  and
and  are compact, by (4.26) and Lemmas 2.5(1) and 2.5(2), we can see that
are compact, by (4.26) and Lemmas 2.5(1) and 2.5(2), we can see that

Hence by (1),  is continuous on
is continuous on  .
.
Let  ,
,  , and
, and  be defined as in the proof of Lemma 4.5(2).
be defined as in the proof of Lemma 4.5(2).
If  , also by (4.26), we can see that
, also by (4.26), we can see that  for
for  . It follows that
. It follows that  and thus
and thus  is strict decreasing on
is strict decreasing on  .
.
If  , then
, then  for
for  . This implies that
. This implies that  with
with  .) Hence the fifth lemma follows.
.) Hence the fifth lemma follows.
Lemma 4.10.
(1) exists if and only if
exists if and only if  is nonempty, where
is nonempty, where  is defined by (4.1)(b).
is defined by (4.1)(b).
-
(2)
If
 solves (4.25) for
solves (4.25) for 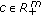 and
and  , then
, then 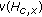 exists with
exists with 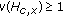 ,
, 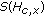 is nonempty with
is nonempty with  for
for  , and
, and  for
for 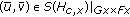 .
.
Proof.
Since  is continuous on
is continuous on  , by Lemma 2.5(1), it is easy to see that
, by Lemma 2.5(1), it is easy to see that

(1)By (4.29) and with the same method as in proving Lemma 4.6(3), we can show that (1) is true. (Indeed, we only need to prove the necessary part. If  exists, then by (4.29), there exists
exists, then by (4.29), there exists  such that
such that  . Hence
. Hence  is nonempty.)
is nonempty.)
(2)If  solves (4.25) for
solves (4.25) for  and
and  , then from Lemma 4.9 we know that
, then from Lemma 4.9 we know that  exists with
exists with  , and there is a unique
, and there is a unique  such that
such that  . In particular,
. In particular,  is the biggest number that makes (4.25) solvable for
is the biggest number that makes (4.25) solvable for  and
and  .
.
Applying the same method as in proving Lemma 4.7(1), we can show that  exists with
exists with  . (In fact, let
. (In fact, let

Then  . We need to show that
. We need to show that  .
.
Since  solves (4.25) for
solves (4.25) for  and
and  , there exist
, there exist  and
and  such that
such that  . It follows that
. It follows that  for any
for any  , hence
, hence  On the other hand, by the definition of
On the other hand, by the definition of  , we have
, we have  for any
for any  . By (4.29)(a) and (4.1)(b), there exists
. By (4.29)(a) and (4.1)(b), there exists  such that
such that  which implies by (4.26) that
which implies by (4.26) that  for any
for any  . Hence from Lemma 4.9,
. Hence from Lemma 4.9,  solves (4.25), and
solves (4.25), and  . Therefore,
. Therefore,  exist with
exist with  .) So we conclude from (1) and Remark 2.2 that (2) is true. This completes the proof.
.) So we conclude from (1) and Remark 2.2 that (2) is true. This completes the proof.
Lemma 4.11.
If  , then Theorem 4.2(2) is true.
, then Theorem 4.2(2) is true.
Proof.
-
(i)
If
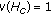 , then by Lemma 4.6(3) and Remark 2.2,
, then by Lemma 4.6(3) and Remark 2.2, 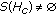 and
and 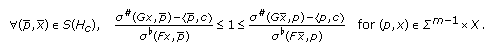 (4.31)
(4.31)
By the same proof of (4.21) we can show that

Combining this with Lemma 4.5(1) and using Remark 2.2(2), we have

As  by (4.4), applying Lemma 2.5(3) to the function
by (4.4), applying Lemma 2.5(3) to the function  on
on  , we obtain that, for each
, we obtain that, for each  ,
,

Since  is u.s.c. on
is u.s.c. on  , from (4.34) there exists
, from (4.34) there exists  such that
such that

Hence,  This implies that
This implies that  solves (4.25) for
solves (4.25) for  and any
and any  . So we conclude from Lemma 4.10 and Remark 2.2(2) that
. So we conclude from Lemma 4.10 and Remark 2.2(2) that

On the other hand, by (4.1),  . Combining this with (4.36), it follows that, for each
. Combining this with (4.36), it follows that, for each  and each
and each  ,
,

Hence, also by (4.1),  . This implies that, for each
. This implies that, for each  and there exists
and there exists  such that
such that  So we obtain
So we obtain

By using the same method as in proving (1) (2) of Theorem 3.2, we conclude that
(2) of Theorem 3.2, we conclude that  and there exists
and there exists  such that
such that  . Hence Theorem 4.2(2) is true.
. Hence Theorem 4.2(2) is true.
Lemma 4.12.
If Theorem 4.2(3) holds,then  .
.
Proof.
If Theorem 4.2(3) holds, then  solves both (1.4) and (1.5), and by Lemma 4.7(1),
solves both (1.4) and (1.5), and by Lemma 4.7(1),  exists with
exists with  .
.
Now we let  ,
,  , and
, and  satisfy
satisfy  and
and  , then we have
, then we have  for
for  and
and  (where
(where  This implies by (4.1) that
This implies by (4.1) that

Combining this with the fact that  and using Remark 2.2 and (4.1), we obtain that
and using Remark 2.2 and (4.1), we obtain that

Hence,  .
.
Proof of Theorem 4.2.
Since (2) (3) of is clear, Theorem 4.2 follows immediately from Lemmas 4.11 and 4.12.
(3) of is clear, Theorem 4.2 follows immediately from Lemmas 4.11 and 4.12.
5. Conclusion
Based on the generalized and multivalued input-output inequality models, in this paper we have considered three types of set-valued inequality systems (namely, (1.3)–(1.5)) and two corresponding solvability questions. By constructing some auxiliary functions and studying their minimax and saddle point properties with the nonlinear analysis approaches, three solvability theorems (i.e., Theorems 3.2, 4.1, and 4.2) composed of necessary and sufficient conditions regarding these inequality systems have been obtained.
References
Leontief EW: Input-Output Analysis. Pergamon Press, Oxford, UK; 1985.
Leontief EW: Input-Output Analysis. 2nd edition. Oxford University Press, New York, NY, USA; 1986.
Miller RE, Blair PD: Input-Output Analysis: Foundations and Extension. Prentice-Hall, Englewood Cliffs, NJ, USA; 1985.
Medvegyev P: A general existence theorem for von Neumann economic growth models. Econometrica 1984, 52(4):963–974. 10.2307/1911193
Bidard C, Hosoda E: On consumption baskets in a generalized von Neumann model. International Economic Review 1987, 28(2):509–519. 10.2307/2526740
Liu YF: Some results on a class of generalized Leontief conditional input output inequalities. Acta Mathematicae Applicatae Sinica 2005, 28(3):506–516.
Liu Y, Zhang Q: Generalized input-output inequality systems. Applied Mathematics and Optimization 2006, 54(2):189–204. 10.1007/s00245-006-0858-1
Liu Y: A set-valued type inequality system. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(11):4131–4142. 10.1016/j.na.2007.10.043
Aubin J-P, Ekeland I: Applied Nonlinear Analysis, Pure and Applied Mathematics. John Wiley & Sons, New York, NY, USA; 1984:xi+518.
Aubin J-P: Mathematical Methods of Game and Economic Theory, Studies in Mathematics and Its Applications. Volume 7. North-Holland, Amsterdam, The Netherlands; 1979:xxxii+619.
Aubin J-P: Optima and Equilibria: An Introduction to Nonlinear Analysis, Graduate Texts in Mathematics. Volume 140. 2nd edition. Springer, Berlin, Germany; 1998:xviii+429.
Holmes RB: Geometric Functional Analysis and Applications. Springer, Berlin, Germany; 1974.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Liu, Y. Solvability Criteria for Some Set-Valued Inequality Systems. J Inequal Appl 2010, 543061 (2010). https://doi.org/10.1155/2010/543061
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/543061
 . Indeed, if
. Indeed, if  is compact and
is compact and 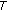 is continuous, compact valued with
is continuous, compact valued with 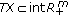 , then
, then 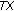 is compact and there is
is compact and there is  with
with 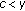 for
for 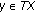 . Hence
. Hence  solves (1.2) but does not solve (1.3).
solves (1.2) but does not solve (1.3).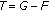 . However, this type of result is trivial because it depends only on the property of
. However, this type of result is trivial because it depends only on the property of  but not on the respective information of
but not on the respective information of 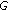 and
and 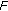 . This opinion is also applicable to (1.3) and (1.5).
. This opinion is also applicable to (1.3) and (1.5).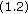 in [
in [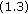 and
and 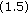 in [
in [ (
(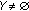 ), and define
), and define 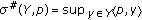 ,
, 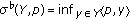 (
(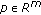 ). Then
). Then 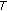 is said to be upper hemicontinuous (in short, u.h.c.) if
is said to be upper hemicontinuous (in short, u.h.c.) if 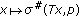 is u.s.c. on
is u.s.c. on  for any
for any 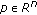 .
.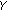 is a convex set and
is a convex set and  a subset of
a subset of  , one claims that
, one claims that 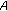 is an extremal subset of
is an extremal subset of 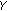 if
if 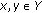 and
and 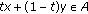 for some
for some 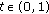 entails
entails  .
.  is an extremal point of
is an extremal point of 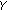 if
if 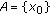 is an extremal subset of
is an extremal subset of 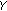 , and the set of all extremal points of
, and the set of all extremal points of  is denoted by ext
is denoted by ext 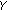 .
.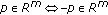 and
and 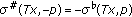 , we can see that
, we can see that 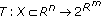 is u.h.c. if and only if
is u.h.c. if and only if  is l.s.c. on
is l.s.c. on 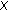 for any
for any 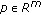 .
. on
on 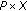 ,
, 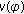 exists if and only if
exists if and only if  , and
, and 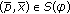 if and only if
if and only if 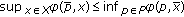 if and only if
if and only if  for any
for any 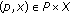 . If
. If 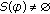 , then
, then 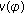 exists, and
exists, and 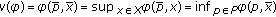 for any
for any  . The same properties are also true for
. The same properties are also true for 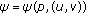 on
on  . Moreover, we have
. Moreover, we have 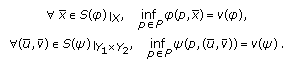
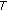 is u.s.c., then
is u.s.c., then 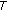 is u.h.c.
is u.h.c.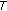 is u.s.c. with closed values, then
is u.s.c. with closed values, then  is closed.
is closed.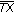 (the closure of
(the closure of 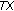 ) is compact and
) is compact and 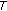 is closed, then
is closed, then 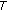 is u.s.c.
is u.s.c.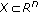 is compact and
is compact and  is u.s.c. with compact values, then
is u.s.c. with compact values, then 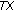 is compact in
is compact in 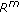 .
.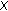 is convex (or compact) and
is convex (or compact) and  are convex (or u.s.c. with compact values), then
are convex (or u.s.c. with compact values), then 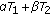 are also convex (or u.s.c.) for all
are also convex (or u.s.c.) for all 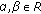 .
.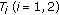 are convex,
are convex, 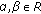 ,
, 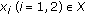 , and
, and 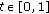 , then
, then 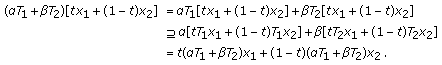
 is compact.
is compact. is convex or l.s.c. (resp., concave or u.s.c.) on
is convex or l.s.c. (resp., concave or u.s.c.) on 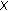 for
for 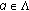 and
and 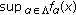 (resp.,
(resp.,  ) is finite for
) is finite for 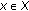 , then
, then 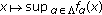 (resp.,
(resp., 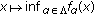 ) is also convex or l.s.c. (resp., concave or u.s.c.) on
) is also convex or l.s.c. (resp., concave or u.s.c.) on  .
.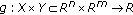 is l.s.c. (or u.s.c.) and
is l.s.c. (or u.s.c.) and 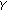 is compact, then
is compact, then 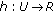 defined by
defined by  (or
(or  defined by
defined by 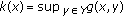 ) is also l.s.c. (or u.s.c.).
) is also l.s.c. (or u.s.c.).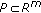 ,
, 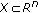 be convex compact, and let
be convex compact, and let 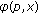 be defined on
be defined on 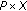 . If, for each
. If, for each 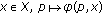 is convex and l.s.c. and, for each
is convex and l.s.c. and, for each 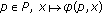 is concave and u.s.c., then
is concave and u.s.c., then 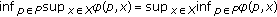 and there exists
and there exists 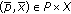 such that
such that 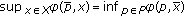 .
.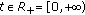 ,
,  exists and
exists and 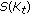 is nonempty. Moreover,
is nonempty. Moreover,  solves (4.3) if and only if
solves (4.3) if and only if 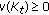 if and only if
if and only if 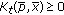 for
for 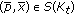 .
. is continuous and strictly decreasing on
is continuous and strictly decreasing on 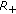 with
with  .
. is convex and u.s.c. with nonempty convex compact values for each
is convex and u.s.c. with nonempty convex compact values for each  . Since
. Since  for
for  , applying Lemma 2.4 to
, applying Lemma 2.4 to 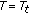 and substituting
and substituting  for
for 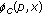 , we know that (1) is true.
, we know that (1) is true. and
and 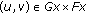 , the function
, the function 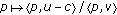 is continuous on
is continuous on  , from Lemma 2.5(1), we can see that
, from Lemma 2.5(1), we can see that 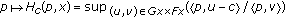
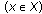 and
and 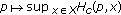 are l.s.c., hence (1) is true.
are l.s.c., hence (1) is true.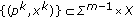 is a sequence with
is a sequence with 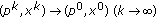 , then for each
, then for each  , there exist
, there exist  and
and  such that
such that 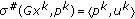 ,
, 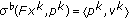 . Since
. Since 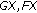 are compact and
are compact and 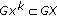 ,
, 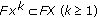 , we may choose
, we may choose  and
and  such that
such that 
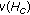 exists. By (1) and (2), there exist
exists. By (1) and (2), there exist 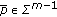 and
and  such that
such that solves(1.4), then
solves(1.4), then 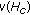 exists with
exists with  .
. solves (1.4), then
solves (1.4), then  solves (4.3). From Lemma 4.5, we know that
solves (4.3). From Lemma 4.5, we know that 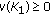 , and there is a unique
, and there is a unique 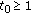 such that
such that 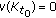 . Moreover, also from Lemma 4.5,
. Moreover, also from Lemma 4.5, 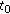 is the biggest number that makes (4.3) solvable, and thus
is the biggest number that makes (4.3) solvable, and thus  solves (4.3) if and only if
solves (4.3) if and only if  . We will prove that
. We will prove that 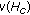 exists with
exists with  . Let
. Let 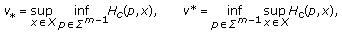
 solves (4.25) for
solves (4.25) for 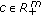 and
and  , then
, then 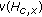 exists with
exists with 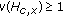 ,
, 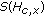 is nonempty with
is nonempty with  for
for  , and
, and  for
for 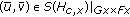 .
.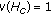 , then by Lemma 4.6(3) and Remark 2.2,
, then by Lemma 4.6(3) and Remark 2.2, 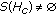 and
and