- Research Article
- Open access
- Published:
Oscillations of Second-Order Neutral Impulsive Differential Equations
Journal of Inequalities and Applications volume 2010, Article number: 493927 (2010)
Abstract
Necessary and sufficient conditions are established for oscillation of second-order neutral impulsive differential equation  ,
,  ,
,  where the coefficients
where the coefficients  ;
;  ,
,  and
and  .
.
1. Introduction
Oscillation theory is one of the directions which initiated the investigations of the qualitative properties of differential equations. This theory started with the classical works of Sturm and Kneser, and still attracts the attention of many mathematicians as much for the interesting results obtained as for their various applications.
In 1989 the paper of Gopalsamy and Zhang [1] was published, where the first investigation on oscillatory properties of impulsive differential equations was carried out.
The monograph [2] is the first book to present systematically the results known up to 1998, and to demonstrate how well-know mathematical techniques and methods, after suitable modification, can be applied in proving oscillatory theorems for impulsive differential equations.
Recently, the oscillatory theory of differential equations has been the subject of intensive research [3–8]. In particular, many remarkable results for the oscillatory properties of various classes of impulsive differential equations can be found in the literature [2, 9–11].
The notion of characteristic system was first introduced by Bainov and Simeonov [2]; it can be used in obtaining of various necessary and sufficient conditions for oscillation of constant coefficients linear impulsive differential equations of first order with one or several deviating arguments.
As we know, on the case when we investigate constant coefficients linear neutral differential equations without impulse, it is very significant to obtain necessary and sufficient conditions for the oscillation corresponding to their characteristic equations; some necessary and sufficient conditions (in terms of the characteristic equation) for the oscillation of all solutions of first-or second-order neutral differential equations were established in [12–20]. However, the oscillation theory of the second order impulsive differential equations is not yet perfect compared to the second order differential equations with deviating argument (see [2]). For example, due to some obstacles of theoretical and technical character in handling with constant coefficients linear impulsive differential equations of second or higher order, there are no results which studied the necessary and sufficient conditions in monograph [2]. How to establish the necessary and sufficient conditions for second order constant coefficients linear impulsive differential equations corresponding to their characteristic systems? This is also an important open problem (see monograph [2]). In this paper, we study and solve this problem for a class of linear impulsive differential equations of second order with advanced argument.
We shall restrict ourselves to the studying of impulsive differential equations for which the impulse effects take part at fixed moments  . Considering the second order neutral impulsive differential equations with constant coefficients
. Considering the second order neutral impulsive differential equations with constant coefficients

where

Throughout this paper, we assume that the sequence  of the moments of impulse effects has the following properties (H):
of the moments of impulse effects has the following properties (H):
 and
and 
Here considering  -periodic and
-periodic and  -periodic equation with
-periodic equation with  , we suppose that the sequence
, we suppose that the sequence  satisfies the following conditions.
satisfies the following conditions.
There exist nonnegative integers  and
and  such that
such that

This condition is equivalent to the next one.
There exist nonnegative integers  and
and  such that
such that

Here  denotes the number of the points
denotes the number of the points  , lying in the interval
, lying in the interval  .
.
As customary, a solution of (1.1) is said to be oscillatory if it has arbitrarily large zeros. Otherwise the solution is called nonoscillatory. As usual, we use the term "finally" to mean "for sufficiently large  ". For other related notions, see monographs [2, 9–11] for details.
". For other related notions, see monographs [2, 9–11] for details.
We clearly see that (1.1) is an equation without impulse and  together with
together with  if
if  in (H1.2) or (H1.3). In this case, (1.1) reduces to
in (H1.2) or (H1.3). In this case, (1.1) reduces to

2. Asymptotic Behavior of the Solutions
In the sequence, we assume that conditions (H1.1)–(H1.3) hold, and

Lemma 2.1.
Suppose that  is defined by (2.1). If (1.1) has a finally positive solution
is defined by (2.1). If (1.1) has a finally positive solution  , then
, then
(a) is also a solution of (1.1), that is,
is also a solution of (1.1), that is,

(b)

or

-
(c)
If (2.3) holds, then
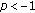 .
. -
(d)
If
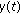 is a solution of (1.1), then
is a solution of (1.1), then

is also a solution of (1.1).
Proof.
-
(a)
It follows from condition (H1.2) that if
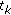 is a moment of impulse effect, then
is a moment of impulse effect, then  is also a such moment. Thus,
is also a such moment. Thus,  is also a solution of (1.1) since (1.1) is a linear one with constant coefficients. Therefore,
is also a solution of (1.1) since (1.1) is a linear one with constant coefficients. Therefore,  is a solution of (1.1) which follows from the linear combination of solutions.
is a solution of (1.1) which follows from the linear combination of solutions. -
(b)
We clearly see that

which imply that  is strictly increasing and so either
is strictly increasing and so either

or

We clearly see that (2.7) implies inequality (2.4). Now, we assume that inequality (2.8) holds. We first prove that  .
.
In fact, integrating (2.6) from  to
to  and letting
and letting  we get
we get

hence

which implies that  is integrable in
is integrable in  ,
,

Then from (2.1) we get

and so  . (Otherwise, by L'Hospital's rule, we have
. (Otherwise, by L'Hospital's rule, we have  when
when  then
then  ). Thus
). Thus  increases to zero, which implies that eventually
increases to zero, which implies that eventually

Then  decreases and in view of
decreases and in view of  , we have
, we have

hence

-
(c)
For the sake of contradiction, assume that (2.3) holds and
 . From parts (a) and (b), we know that
. From parts (a) and (b), we know that 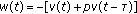 is also a positive solution of (1.1), therefore,
is also a positive solution of (1.1), therefore,

which implies that

this contradicts with the fact that  is a decreasing function.
is a decreasing function.
-
(d)
Let
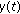 be a solution of (1.1), and
be a solution of (1.1), and

We prove that  is also a solution of (1.1).
is also a solution of (1.1).
Clearly,  satisfies
satisfies

Since  is a solution of (1.1), so
is a solution of (1.1), so

That is,

which implies that  is also a solution of (1.1).
is also a solution of (1.1).
Let  and
and  be the set of all functions of the form
be the set of all functions of the form

where  is a solution of (1.1) which satisfies (2.3) and (2.4), respectively. In view of Lemma 2.1, either
is a solution of (1.1) which satisfies (2.3) and (2.4), respectively. In view of Lemma 2.1, either  or
or  is nonempty. Also, an argument similar to that of Lemma 2.1 shows that each function
is nonempty. Also, an argument similar to that of Lemma 2.1 shows that each function  is a solution of (1.1), and satisfies
is a solution of (1.1), and satisfies

Also, there is a solution  of (1.1) which satisfies (2.3) if
of (1.1) which satisfies (2.3) if  or (2.4) if
or (2.4) if  such that
such that

Clearly, every function  satisfies
satisfies

while every function  satisfies
satisfies

Furthermore,

Finally,  (
( , resp.) and
, resp.) and  (
( , resp.).
, resp.).
3. Oscillation of the Unbounded Solutions
First, we will assume that  (i.e.,
(i.e., 
The present section is devoted to the characterizing of the oscillatory properties of solutions of the periodic neutral impulsive differential equation (1.1).
We are looking for a positive solution of (1.1) having the form

where  are constants.
are constants.
Substituting (3.1) in (1.1), and from condition (H1.3), we obtain the characteristic system of (1.1) as follows:

As  , the characteristic system is equivalent to
, the characteristic system is equivalent to

Equation (3.3) is called a characteristic equation, corresponding to the (1.1).
Theorem 3.1.
If the conditions (H1.1)–(H1.3) hold, then the following assertions are equivalent.
(a)Each unbounded regular solution of (1.1) is oscillatory.
(b)The characteristic equation (3.3) has no positive real roots.
The proof of (a)  (b) is obvious. In fact, if the characteristic equation (3.3) has a real root
(b) is obvious. In fact, if the characteristic equation (3.3) has a real root  , then we clearly see that
, then we clearly see that  and therefore the function
and therefore the function

is an unbounded positive solution of (1.1).
The proof of (b)  (a) is quite complicated and will be accomplished by establishing a series of lemmas.
(a) is quite complicated and will be accomplished by establishing a series of lemmas.
We assume that (3.3) has no positive real roots and, for the sake of contradiction, we assume that (1.1) has an unbounded finally positive solution 
Lemma 3.2.
If (1.1) has an eventually positive solution, then
(a)
-
(b)
There exists a positive constant
 such that
such that

Proof.
-
(a)
Otherwise,
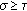 , therefore
, therefore  , but
, but  is impossible because the characteristic equation
is impossible because the characteristic equation 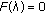 has no positive real roots.
has no positive real roots. -
(b)
We have
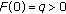 ,
, 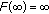 and so
and so 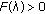 for all
for all 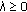 .
.
Hence there exists a positive constant  such that
such that

which completes the proof of Lemma 3.2.
For each function  define the set
define the set

Clearly,  and if
and if  then
then  . Therefore,
. Therefore,  is a nonempty subinterval of
is a nonempty subinterval of  .
.
Lemma 3.3.
For  and
and  , we have the folloeing.
, we have the folloeing.
-
(a)
If
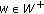 and
and 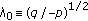 , then
, then 
(b) is bounded above by a positive constant
is bounded above by a positive constant  , for all
, for all  .
.
(c)If  and
and  , then
, then

Proof.
-
(a)
From (2.23), (2.26) and the fact that
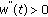 and
and 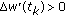 , we have
, we have 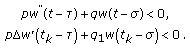 (3.9)
(3.9)
That is,

The increasing nature of  and the fact that
and the fact that  imply that
imply that

which shows that

By integrating (3.10) from  to
to  with
with  we get
we get

From the fact that  and
and  , we have
, we have

By integrating again from  to
to  with
with  we get
we get

from the fact that  and
and  together with
together with  , we have
, we have

Let  then
then

That is,

where 
Now let  such that
such that  then (3.18) and the increasing nature of
then (3.18) and the increasing nature of  imply that
imply that

By integrating (2.24) from  to
to  with
with  we get
we get

By integrating again from  to
to  with
with  we have
we have

Let  , then
, then

Combining (2.24), (3.19), and (3.22), we have

which shows that

and  is not in the set
is not in the set  for all
for all  that is,
that is,  is bounded above by the positive constant
is bounded above by the positive constant  , for all
, for all  .
.
-
(c)
Let

then

Therefore,


We clearly see that  is a nondecreasing function and so if the conclusion in part (c) was false, then
is a nondecreasing function and so if the conclusion in part (c) was false, then

From (3.27), (3.28), and (3.29), we know that

and so

which together with the hypothesis yield that

Hence


Let

Then by Lemma 2.1(d) and the linear combination of solutions, we know that  is a solution of (1.1). From (3.29), (3.33), and (3.34), we have
is a solution of (1.1). From (3.29), (3.33), and (3.34), we have

Now using  instead of
instead of  in (2.1) and the hypothesis that
in (2.1) and the hypothesis that  together with a similar argument as in (2.4), we get
together with a similar argument as in (2.4), we get

But (3.36) implies that

and the contradiction completes the proof of Lemma 3.3.
By integrating both sides of (2.23) from  to
to  , we get
, we get

That is,

where

As  is a solution of (1.1) and
is a solution of (1.1) and  satisfying (2.24), it follows from (3.40) that if
satisfying (2.24), it follows from (3.40) that if  then
then

where  is the constant given by (3.41).
is the constant given by (3.41).
Lemma 3.4.
Suppose that  and
and  are the constants defined in Lemma 3.2
are the constants defined in Lemma 3.2 and Lemma 3.3
and Lemma 3.3 , respectively. If
, respectively. If  ,
,  and
and

then

where

Proof.
Clearly  is an element of
is an element of  . From Lemma 3.3(c), we have
. From Lemma 3.3(c), we have

Then from (3.45) we get

By integrating (3.46) from  to
to  , we obtain
, we obtain

and so

Let

then

By integrating it from  to
to  , we have
, we have

Set

as defined in the proof of Lemma 3.3(c).
We clearly see that  is a nondecreasing function, therefore,
is a nondecreasing function, therefore,

Let

Using (3.45), (3.47), (3.49), (3.54), the increasing nature of  ,
,  and the fact that
and the fact that

we have

As

we see that for sufficiently large  ,
,

and as  , so
, so

Then

Analogously,

Therefore, the proof of Lemma 3.4 is completed.
Now, considering the sequence of functions

where  is the function defined by (3.45),
is the function defined by (3.45),  is the number defined in Lemma 3.3(a),
is the number defined in Lemma 3.3(a),

The repeated applications of Lemma 3.4 lead to

Clearly

which contradicts with the fact proved in Lemma 3.3(b) that

Therefore, the proof of Theorem 3.1 is completed.
4. Oscillation of the Bounded Solutions
In Section 2, we complete the case of  . Now we consider the conditions ensuring oscillation of the case of
. Now we consider the conditions ensuring oscillation of the case of  , that is, considering the conditions ensuring oscillation of the bounded solutions of (1.1). Then in view of Lemma 2.1(c),
, that is, considering the conditions ensuring oscillation of the bounded solutions of (1.1). Then in view of Lemma 2.1(c),  .
.
We are looking for a positive solution of (1.1) with the form

where  are constants.
are constants.
Substituting (4.1) in (1.1), just like in Section 2, we can obtain the characteristic equation of (1.1) as follows:

where

Theorem 4.1.
If the condition (H) holds, then the following assertions are equivalent.
-
(a)
Each bounded regular solution of the equation (1.5) is oscillatory.
-
(b)
The characteristic equation (4.2) has no real roots
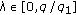 .
.
The proof of (a)  (b) is obvious. In fact, if the characteristic equation (4.2) has a real root
(b) is obvious. In fact, if the characteristic equation (4.2) has a real root  , then
, then  and
and  , therefore the function
, therefore the function

is a bounded positive solution of (1.1).
The proof of (b)  (a) is quite complicated and will be accomplished by establishing a series of lemmas.
(a) is quite complicated and will be accomplished by establishing a series of lemmas.
As in Section 3 we assume, without further mention, that (1.2) holds. We also assume that (4.2) has no real roots  . For the sake of contradiction, we assume that (1.1) has a bounded finally positive solution
. For the sake of contradiction, we assume that (1.1) has a bounded finally positive solution  .
.
Also like the case in Section 3, for each function  define the set
define the set

Clearly,  and if
and if  then
then  . That is,
. That is,  is a nonempty subinterval of
is a nonempty subinterval of  .
.
Lemma 4.2.
There exists a positive constant  such that
such that

Proof.
We clearly see that

and so there exists a positive constant  such that
such that

Lemma 4.3.
-
(a)
If
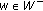 and
and  with
with 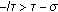 , then
, then 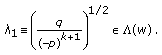 (4.9)
(4.9)
-
(b)
If
 and
and 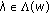 , then
, then

(c) is bounded above by a positive constant
is bounded above by a positive constant  for any
for any  .
.
Proof.
-
(a)
Let
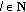 with
with 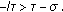
For  we have
we have

and so

That is,

as

So

That is,

-
(b)
Let

then

Let

then

Therefore,  is a nondecreasing function.
is a nondecreasing function.
Note that

We know that  and so
and so

-
(c)
Otherwise,

Then from part (b)

we know that the function  is nonincreasing and
is nonincreasing and

or

This contradicts with(3.54); therefore, The proof of Lemma 4.3 is completed.
Lemma 4.4.
Suppose that  is a constant defined in Lemma 4.2 and
is a constant defined in Lemma 4.2 and  . If
. If  ,
,  and
and

then

where

and

Proof.
Clearly,  is an element of
is an element of  If
If

then

Let

then

By integrating (4.34) from  to
to  we get
we get

Let  then
then

Integrating (4.32) from  to
to  we get
we get

That is,

By integrating again from  to
to  we find
we find

Then from (4.35) we have

and

Using (4.29) and (4.32) together with (4.38)–(4.41), we see that

Therefore,

For  and
and  , we have
, we have  . From the fact that
. From the fact that  is nonincreasing, we clearly see that
is nonincreasing, we clearly see that  . Therefore,
. Therefore,

Analogously, we have

So

Therefore, the proof of Lemma 4.4 is completed.
Now, we consider the sequence of functions

where,  is the function
is the function  defined in (4.29),
defined in (4.29),

The repeated applications of Lemma 4.4 lead to

Clearly,

which contradicts with the fact proved in Lemma 4.3(c) that  is bounded above for any
is bounded above for any  . Therefore, the proof of Theorem 4.1 is completed.
. Therefore, the proof of Theorem 4.1 is completed.
Remark 4.5.
Let  , then (1.1) reduces to (1.5), and (3.3) and (4.2) reduce to
, then (1.1) reduces to (1.5), and (3.3) and (4.2) reduce to

From our Theorems 3.1 and 4.1, we get the following well-known results:
Corollary 4.6.
The following assertions are equivalent.
-
(a)
Each unbounded regular solution of the equation (1.5) is oscillatory.
(b)The characteristic equation (4.51) has no positive real roots.
Corollary 4.7.
The following assertions are equivalent.
(a)Each bounded regular solution of the equation (1.5) is oscillatory.
(b)The characteristic equation (4.51) has no real root  .
.
References
Gopalsamy K, Zhang BG: On delay differential equations with impulses. Journal of Mathematical Analysis and Applications 1989, 139(1):110–122. 10.1016/0022-247X(89)90232-1
Bainov D, Simeonov P: Oscillation Theory of Impulsive Differential Equations. International Publications, Orlando, Fla, USA; 1998.
Bainov DD, Mishev DP: Oscillation Theory for Neutral Differential Equations with Delay. Adam Hilger, Bristol, UK; 1991.
Győri I, Ladas G: Oscillation Theory of Delay Differential Equations. The Clarendon Press Oxford University, New York, NY, USA; 1991.
Erbe LH, Kong Q, Zhang BG: Oscillation Theory for Functional-Differential Equations. Volume 190. Marcel Dekker, New York, NY, USA; 1995.
Agarwal RP, Grace SR, O'Regan D: Oscillation Theory for Difference and Functional Differential Equations. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2000.
Agarwal RP, Grace SR, O'Regan D: Oscillation Theory for Second Order Dynamic Equations. Volume 5. Taylor and Francis, London, UK; 2003.
Agarwal RP, Bohner M, Li W-T: Nonoscillation and Oscillation: Theory for Functional Differential Equations. Volume 267. Marcel Dekker, New York, NY, USA; 2004.
Lakshmikantham V, Bainov DD, Simeonov PS: Theory of Impulsive Differential Equations. Volume 6. World Scientific Publishing Company, Teaneck, NJ, USA; 1989.
Bainov D, Simeonov P: Impulsive Differential Equations: Periodic Solutions and Applications. Volume 66. Longman Scientific and Technical, Harlow, Uk; 1993.
Bainov DD, Simeonov PS: Impulsive Differential Equations. Volume 28. World Scientific Publishing Company, River Edge, NJ, USA; 1995.
Ladas G, Sficas YG, Stavroulakis IP: Necessary and sufficient conditions for oscillations of higher order delay differential equations. Transactions of the American Mathematical Society 1984, 285(1):81–90. 10.1090/S0002-9947-1984-0748831-8
Sficas YG, Stavroulakis IP: Necessary and sufficient conditions for oscillations of neutral differential equations. Journal of Mathematical Analysis and Applications 1987, 123(2):494–507. 10.1016/0022-247X(87)90326-X
Grove EA, Ladas G, Meimaridou A: A necessary and sufficient condition for the oscillation of neutral equations. Journal of Mathematical Analysis and Applications 1987, 126(2):341–354. 10.1016/0022-247X(87)90045-X
Arino O, Győri I: Necessary and sufficient condition for oscillation of a neutral differential system with several delays. Journal of Differential Equations 1989, 81(1):98–105. 10.1016/0022-0396(89)90179-4
Grammatikopoulos MK, Stavroulakis IP: Necessary and sufficient conditions for oscillation of neutral equations with deviating arguments. Journal of the London Mathematical Society. Second Series 1990, 41(2):244–260. 10.1112/jlms/s2-41.2.244
Kulenović MRS, Ladas G, Sficas YG: Oscillations of second order linear delay differential equations. Applicable Analysis 1988, 27(1–3):109–123.
Ladas G, Partheniadis EC, Sficas YG: Necessary and sufficient conditions for oscillations of second-order neutral equations. Journal of Mathematical Analysis and Applications 1989, 138(1):214–231. 10.1016/0022-247X(89)90332-6
Bilchev SJ, Grammatikopoulos MK, Stavroulakis IP: Oscillations of second-order neutral differential equations with deviating arguments. In Oscillation and Dynamics in Delay Equations (San Francisco, CA, 1991), Contemporary Mathematics. Volume 129. American Mathematical Society, Providence, RI, USA; 1992:1–21.
Wang Z: A necessary and sufficient condition for the oscillation of higher-order neutral equations. The Tohoku Mathematical Journal 1989, 41(4):575–588. 10.2748/tmj/1178227728
Acknowledgment
The authors wish to thank the anonymous referee for the very careful reading of the manuscript and fruitful comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Cheng, JF., Chu, YM. Oscillations of Second-Order Neutral Impulsive Differential Equations. J Inequal Appl 2010, 493927 (2010). https://doi.org/10.1155/2010/493927
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/493927
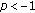 .
.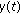 is a solution of (1.1), then
is a solution of (1.1), then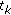 is a moment of impulse effect, then
is a moment of impulse effect, then  is also a such moment. Thus,
is also a such moment. Thus,  is also a solution of (1.1) since (1.1) is a linear one with constant coefficients. Therefore,
is also a solution of (1.1) since (1.1) is a linear one with constant coefficients. Therefore,  is a solution of (1.1) which follows from the linear combination of solutions.
is a solution of (1.1) which follows from the linear combination of solutions. . From parts (a) and (b), we know that
. From parts (a) and (b), we know that 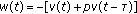 is also a positive solution of (1.1), therefore,
is also a positive solution of (1.1), therefore,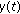 be a solution of (1.1), and
be a solution of (1.1), and such that
such that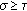 , therefore
, therefore  , but
, but  is impossible because the characteristic equation
is impossible because the characteristic equation 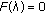 has no positive real roots.
has no positive real roots.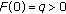 ,
, 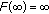 and so
and so 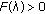 for all
for all 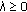 .
.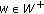 and
and 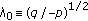 , then
, then 
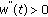 and
and 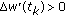 , we have
, we have 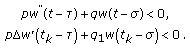
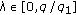 .
.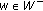 and
and  with
with 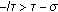 , then
, then 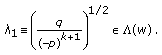
 and
and 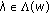 , then
, then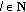 with
with