- Research Article
- Open access
- Published:
Complementary Inequalities Involving the Stolarsky Mean
Journal of Inequalities and Applications volume 2010, Article number: 492570 (2010)
Abstract
Let  be a positive integer and
be a positive integer and  ,
,  ,
,  , and
, and  real numbers satisfying
real numbers satisfying  and
and  . It is proved that for the real numbers
. It is proved that for the real numbers  the maximum of the function
the maximum of the function  is attained if and only if
is attained if and only if  of the numbers
of the numbers  are equal to
are equal to  and the other
and the other  are equal to
are equal to  , while
, while  is one of the values
is one of the values  ,
,  , where
, where  denotes the integer part and
denotes the integer part and  represents the Stolarsky mean of
represents the Stolarsky mean of  and
and  of powers
of powers  and
and  Some asymptotic results concerning
Some asymptotic results concerning  are also discussed.
are also discussed.
1. Introduction
Let us begin with some definitions. Given the positive real numbers  and
and  and the real numbers
and the real numbers  and
and  , the difference mean or Stolarsky mean
, the difference mean or Stolarsky mean  of
of  and
and  is defined by (see, e.g., [1] or [2])
is defined by (see, e.g., [1] or [2])

The power mean of power  corresponding to the real numbers
corresponding to the real numbers  is defined by
is defined by

The relation between the Stolarsky mean and the power mean can be written as

It is well known that for fixed  and
and  , we have the inequality
, we have the inequality

with equality for  (independent of
(independent of  ), or for
), or for  (see [3–5] or [6]).
(see [3–5] or [6]).
Shisha and Mond [7] obtained a complementary result which examines the upper bounds of (1.4) for weighted versions of the power means. Also, we have a considerable amount of work regarding the complementary means done by many authors, including Diaz and Metcalf [8], Beck [9], and Páles [10].
Returning to our problem, by defining the function

we obtain

Using the inequalities between power means (1.4),  if and only if
if and only if  therefore
therefore  if and only if
if and only if  This condition is more general than
This condition is more general than  but there are details in the subsequent proofs which would not be satisfied in the other cases.
but there are details in the subsequent proofs which would not be satisfied in the other cases.
As the minimum of  over
over  is
is  (possible only for
(possible only for  ), it is natural to question what the maximum of
), it is natural to question what the maximum of  is, and, eventually, to find the configuration where this is attained. Since
is, and, eventually, to find the configuration where this is attained. Since  the problem of finding the maximum of
the problem of finding the maximum of  only makes sense when all the variables
only makes sense when all the variables  of
of  are restricted to the compact interval
are restricted to the compact interval  .
.
The first theorem in the next section, deals with finding the maximum and the corresponding optimal configuration. The result enables one to obtain elegant proofs for some related inequalities. In the end of the present work we obtain some asymptotic limits relative to the configuration where the maximum of  is attained.
is attained.
2. Results
Theorem 2.1.
Given the positive integer  , the real numbers
, the real numbers  and
and  . Consider the function
. Consider the function  , defined by (1.4). Then the following assertions are true.
, defined by (1.4). Then the following assertions are true.
-
(1)
The function
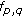 attains its maximum at a point
attains its maximum at a point  if and only if
if and only if 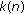 of the variables are equal to
of the variables are equal to  while the other
while the other  are equal to b, where
are equal to b, where 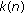 can be
can be 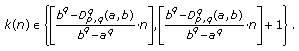 (2.1)
(2.1)
-
(2)
If
 ,
, 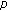 , and
, and 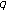 are held fixed while
are held fixed while 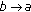 , it can be proven that
, it can be proven that 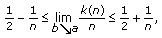 (2.2)
(2.2)
provided the limit exists.
As an application of Theorem 2.1, the following problem (see [3, pages 70–72]) is solved.
Corollary 2.2.
Given the positive integer  , determine the smallest value of
, determine the smallest value of  such that the inequality
such that the inequality

holds true for all positive real numbers 
Theorem 2.3.
Given the positive integer  , the smallest value of
, the smallest value of  such that (2.3) holds true for all positive real numbers
such that (2.3) holds true for all positive real numbers  is
is

In the following theorem we examine the behavior of  when the numbers
when the numbers  ,
,  in Theorem 2.1, are terms of a sequence with certain properties.
in Theorem 2.1, are terms of a sequence with certain properties.
Theorem 2.4.
Consider the sequences  and
and  satisfying
satisfying 
 with
with  and
and  For each
For each  define
define  as in (2.1), for the powers
as in (2.1), for the powers  and
and  Then the
Then the  verifies
verifies

3. Proofs
Proof of Theorem 2.1.
-
(1)
We first prove that the point
 where the maximum of
where the maximum of  is attained lies on the boundary of the hypercube
is attained lies on the boundary of the hypercube 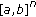 and moreover, it is a vertex. This result is the subject of Lemma 3.1. We then find the configuration where the maximum is realized.
and moreover, it is a vertex. This result is the subject of Lemma 3.1. We then find the configuration where the maximum is realized.
Lemma 3.1.
The function  attains its maximum at the point
attains its maximum at the point  if and only if
if and only if  for all
for all 
Proof of Lemma 3.1.
Since  is continuous on the compact interval
is continuous on the compact interval  , there is a point
, there is a point  where
where  attains its maximum. If
attains its maximum. If  is an interior point of
is an interior point of  , then
, then  for all
for all  therefore
therefore

which implies

for all  However, if
However, if  , then
, then  which clearly is not the maximum of
which clearly is not the maximum of  Consequently,
Consequently,  lies on the boundary of
lies on the boundary of  . Due to symmetry and since
. Due to symmetry and since  there exist
there exist  and
and  such that
such that

If  then
then  For this case, consider the function
For this case, consider the function  defined by
defined by

If the point  where the maximum of
where the maximum of  is attained is interior to
is attained is interior to  , in virtue of Fermat's theorem, we deduce that
, in virtue of Fermat's theorem, we deduce that

for all  This is equivalent to
This is equivalent to

hence

A simple computation shows that

and for this configuration we have

Let us define the function  as
as

and prove it is increasing. Indeed, one finds

where  , and
, and  Since
Since  it follows that
it follows that  so
so  is increasing and the upper bound is
is increasing and the upper bound is

This finally proves that  of the numbers
of the numbers  are equal to
are equal to  while the other
while the other  are equal to
are equal to  as anticipated. This ends the proof of Lemma 3.1.
as anticipated. This ends the proof of Lemma 3.1.
The only thing to be done is to find the value of  for which the expression
for which the expression

attains its maximum.
To do this, consider the function  defined by
defined by

and find the points where the maximum of  is attained in the interval
is attained in the interval  .
.
The critical points of  are found from the equation
are found from the equation

so they satisfy

As seen in the definition of the Stolarsky mean for this case,

It is finally found that  has a single critical point
has a single critical point

which (fortunately) is contained in the interior of 
Taking into account that the second derivative of  is
is

the extremal point  is a point of maximum for
is a point of maximum for  , and also the function
, and also the function  is decreasing on the interval
is decreasing on the interval  . Because
. Because  , we obtain
, we obtain  for
for  , and
, and  for
for  Finally, this means that
Finally, this means that  is increasing on
is increasing on  and decreasing on
and decreasing on  .
.
We conclude that

The maximum of (3.13) is then attained when  takes one of the values
takes one of the values  and
and  , where
, where

The value of this  is to be called
is to be called  from now on.
from now on.
Remark 3.2.
Because in our case

the Stolarsky mean satisfies the strict inequality  , so
, so 
-
(2)
Using the properties of the integer part
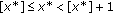 , we obtain
, we obtain  (3.23)
(3.23)
so

It is then enough to work out the limit

On the other hand we have

Due to symmetry the partial derivatives are equal, so the desired limit is

Taking the limit  in (3.23), we obtain that the limit of
in (3.23), we obtain that the limit of  as
as  is confined to the interval
is confined to the interval 
Proof of Theorem 2.3.
Considering  and
and  in Theorem 2.1, we obtain
in Theorem 2.1, we obtain

Out of here, we can immediately obtain the best constant  for which
for which

Following the steps mentioned before, the function gets the maximum only when

where  , or
, or  .
.
This proves that the following inequality holds:

so the best constant  will be
will be


Remark 3.3.
Although appealing, a result involving arbitrary powers  would depend on which the exact value of
would depend on which the exact value of  is (out of the two possibilities). At the same time, the power
is (out of the two possibilities). At the same time, the power  on the righthand-side can only be obtained for
on the righthand-side can only be obtained for 
Proof of Theorem 2.4.
To ease the notations we write  and
and  The following relation holds:
The following relation holds:

Using the notation  the limit can be written as
the limit can be written as

Since the denominator converges to  it only remains to examine the limit
it only remains to examine the limit

which can be written as

It can be proven that the two terms of (3.36) converge to finite limits, and analyze each. From the hypothesis  so the limit of the first term is
so the limit of the first term is

while second term can be written as

Since

the same argument as above can be used to obtain

where

In the end we obtain

References
Stolarsky KB: Generalizations of the logarithmic mean. Mathematics Magazine 1975, 48: 87–92. 10.2307/2689825
Losonczi L, Páles Zs: Minkowski's inequality for two variable difference means. Proceedings of the American Mathematical Society 1998, 126(3):779–789. 10.1090/S0002-9939-98-04125-2
Drâmbe MO: Inequalities—Ideas and Methods. Zalău, Romania, Gil; 2003.
Mitrinović DS, Pečarić JE, Fink AM: Classical and New Inequalities in Analysis, Mathematics and Its Applications (East European Series). Volume 61. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1993:xviii+740.
Mitrinović DS: Analytic Inequalities. Volume 2. Springer, London, UK; 1970:xii+395.
Hardy GH, Litllewod JE, Polya G: Inequalities. Cambridge University Press, Cambridge, UK; 1967.
Shisha O, Mond B: Differences of means. Bulletin of the American Mathematical Society 1967, 73: 328–333. 10.1090/S0002-9904-1967-11737-3
Diaz JB, Metcalf FT: Complementary inequalities. I. Inequalities complementary to Cauchy's inequality for sums of real numbers. Journal of Mathematical Analysis and Applications 1964, 9: 59–74. 10.1016/0022-247X(64)90006-X
Beck E: Über komplementäre Ungleichungen mit drei Mittelwerten. Monatshefte für Mathematik 1975, 80: 13–29. 10.1007/BF01487800
Páles Zs: On complementary inequalities. Publicationes Mathematicae Debrecen 1983, 30(1–2):75–88.
Acknowledgments
The author wishs to express his thanks to T. Trif, who provided significant moral and technical support to finish this paper. The author also thanks the reviewers, whose suggestions and "free gifts'' were of great help. Last but not least, his thanks go to the Marie Curie foundation, which gave him the chance to understand Mathematics and its applications from a researcher's perspective.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Bagdasar, O. Complementary Inequalities Involving the Stolarsky Mean. J Inequal Appl 2010, 492570 (2010). https://doi.org/10.1155/2010/492570
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/492570
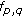 attains its maximum at a point
attains its maximum at a point  if and only if
if and only if 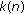 of the variables are equal to
of the variables are equal to  while the other
while the other  are equal to b, where
are equal to b, where 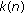 can be
can be 
 ,
,  , and
, and  are held fixed while
are held fixed while 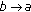 , it can be proven that
, it can be proven that 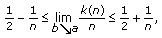
 where the maximum of
where the maximum of  is attained lies on the boundary of the hypercube
is attained lies on the boundary of the hypercube 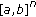 and moreover, it is a vertex. This result is the subject of Lemma 3.1. We then find the configuration where the maximum is realized.
and moreover, it is a vertex. This result is the subject of Lemma 3.1. We then find the configuration where the maximum is realized.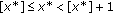 , we obtain
, we obtain 