- Research Article
- Open access
- Published:
On Weighted 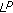 Integrability of Functions Defined by Trigonometric Series
Integrability of Functions Defined by Trigonometric Series
Journal of Inequalities and Applications volume 2010, Article number: 485705 (2010)
Abstract
We introduce a new class of sequences called  and give a sufficient and necessary condition for weighted
and give a sufficient and necessary condition for weighted  integrability of trigonometric series with coefficients to belong to the above class. This is a generalization of the result proved by M. Dyachenko and S. Tikhonov (2009). Then we discuss the relations among the weighted best approximation and the coefficients of trigonometric series. Moreover, we extend the results of B. Wei and D. Yu (2009) to the class
integrability of trigonometric series with coefficients to belong to the above class. This is a generalization of the result proved by M. Dyachenko and S. Tikhonov (2009). Then we discuss the relations among the weighted best approximation and the coefficients of trigonometric series. Moreover, we extend the results of B. Wei and D. Yu (2009) to the class  .
.
1. Introduction
Let  ,
,  , be the space of all
, be the space of all  -power integrable functions
-power integrable functions  of period
of period  equipped with the norm
equipped with the norm

Write

for those  where the series converge. Denote by
where the series converge. Denote by  either
either  or
or  , and let
, and let  be its associated coefficients, that is,
be its associated coefficients, that is,  is either
is either  or
or  .
.
For  and a sequence
and a sequence  let
let

In Subsection 2.1 we generalize the following result.
Theorem 1.1.
Let a nonnegative sequence  ,
,  and
and  . Then
. Then

In the case when  denotes the class
denotes the class  of all decreasing sequences, this theorem was proved in [1–4]; for
of all decreasing sequences, this theorem was proved in [1–4]; for  , the class of quasimonotone sequences, in [5]; for
, the class of quasimonotone sequences, in [5]; for  in [6, 7]; for
in [6, 7]; for  in [8]; and for
in [8]; and for  in [9], where
in [9], where


In [15] Dyachenko and Tikhonov extended Theorem 1.1 to the class  , where
, where  and
and

We have (see [15])

Let  be a nonnegative function defined on the interval
be a nonnegative function defined on the interval  . Denote by
. Denote by  the best approximation of
the best approximation of  by trigonometric polynomials of degree at most
by trigonometric polynomials of degree at most  in the weighted
in the weighted  -norm, that is,
-norm, that is,

where  denotes the set of all trigonometric polynomials of degree at most
denotes the set of all trigonometric polynomials of degree at most  .
.
A sequence  of nonnegative terms is called almost increasing (decreasing) if there exists a constant
of nonnegative terms is called almost increasing (decreasing) if there exists a constant  such that
such that

We say that a weight function  if
if  is defined by the sequence
is defined by the sequence  as follows:
as follows:  ,
,  , and there exist positive constants
, and there exist positive constants  and
and  such that
such that

for all  , and the sequences
, and the sequences  ,
,  are almost decreasing and almost increasing, respectively.
are almost decreasing and almost increasing, respectively.
In Subsection 2.2 we generalize and extend the following results [16].
Theorem 1.2.
Assume that  . If
. If  for some
for some  and
and  , then for
, then for 

Theorem 1.3.
Assume that  . If
. If  for some
for some  and
and  , then for
, then for 

If  and
and  or
or  the above theorem has been obtained by Konyushkov [17] and Leindler [18] for
the above theorem has been obtained by Konyushkov [17] and Leindler [18] for  , respectively.
, respectively.
In order to formulate our new results we define the next class of sequences.
Definition 1.4.
Let  and
and  . One says that a sequence
. One says that a sequence  belongs to
belongs to  , if the relation
, if the relation

holds for all .
.
Note that for  and
and  (see Theorem 2.1(i))
(see Theorem 2.1(i))

Throughout this paper, we use  to denote a positive constant independent of the integer
to denote a positive constant independent of the integer  ;
;  may depend on the parameters such as
may depend on the parameters such as 

 and
and  , and it may have different values in different occurrences.
, and it may have different values in different occurrences.
2. Statement of the Results
We formulate our results as follows.
Theorem 2.1.
Suppose that  . The following properties are true.
. The following properties are true.
(i)For any  , and
, and  there exists a sequence
there exists a sequence  , which does not belong to the class
, which does not belong to the class 
(ii)Let  ,
,  and
and  . If
. If  , then
, then 
(iii)Let  and
and  . If
. If  and
and  , then the classes
, then the classes  and
and  are not comparable.
are not comparable.
2.1. Weighted  -Integrability
-Integrability
Let  and
and  . We define on the interval
. We define on the interval  an even function
an even function  , which is given on the interval
, which is given on the interval  by the formula
by the formula

where  if
if  is an odd number, and
is an odd number, and  if
if  is an even number;
is an even number;  for
for  , and
, and  for
for  .
.
Theorem 2.2.
Let a nonnegative sequence  , where
, where  ,
,  and
and  . If
. If

then  if and only if
if and only if

Theorem 2.3.
Let a nonnegative sequence 
 ,
,  , and
, and  . If
. If

then  if and only if
if and only if

Remark 2.4.
If we take  (and
(and  in Theorem 2.2), then the result of Dyachenko and Tikhonov [15, Theorems
in Theorem 2.2), then the result of Dyachenko and Tikhonov [15, Theorems  and
and  ] follows from Theorems 2.2 and 2.3. By the embedding relations (1.8) and (1.15) we can also derive from Theorem 2.2 the result of You, Zhou, and Zhou [9].
] follows from Theorems 2.2 and 2.3. By the embedding relations (1.8) and (1.15) we can also derive from Theorem 2.2 the result of You, Zhou, and Zhou [9].
2.2. Relations between The Best Approximation and Fourier Coefficients
Theorem 2.5.
Let a nonnegative sequence  , where
, where  ,
,  , and
, and  . If
. If

and (2.3) holds, then

where  .
.
Theorem 2.6.
Let a nonnegative sequence 
 ,
,  and
and  . If
. If

and (2.5) holds, then

where  .
.
Remark 2.7.
If we restrict our attention to the class  then by (1.8) and (1.15) Wei and Yu's result [16] follows from Theorems 2.5 and 2.6.
then by (1.8) and (1.15) Wei and Yu's result [16] follows from Theorems 2.5 and 2.6.
4. Proofs of The Main Results
4.1. Proof of Theorem 2.1
(i)Let  ,
,  and
and

First, we prove that  . Let
. Let

Then for all 

and  . If
. If  then
then

and since

the inequality

does not hold, that is,  does not belong to
does not belong to  .
.
Let  ,
,  and
and  . If
. If  , then exists a natural number
, then exists a natural number  such that
such that  Supposing that
Supposing that  , we have for all
, we have for all 

whence  . Thus
. Thus  .
.
Let  and
and  and let
and let

Supposing that  and
and  , we can prove, similarly as in
, we can prove, similarly as in  , that
, that  ,
,  ,
,  and
and  Therefore the classes
Therefore the classes  and
and  are not comparable.
are not comparable.
4.2. Proof of Theorem 2.2
We prove the theorem for the case when  . The case when
. The case when  can be proved similarly.
can be proved similarly.
Sufficiency. Suppose that (2.3) holds. Then

It is clear that for an odd 

(for  the last sum should be omitted), and for an even
the last sum should be omitted), and for an even 

First, we estimate the following integral:

By (3.3), for  we have
we have

Using (3.2) with  and the inequality
and the inequality

we get

If  then by (3.3), for
then by (3.3), for  we obtain
we obtain

Now, we estimate the following integral:

By (3.3), for  we have
we have

Using (3.2) with  and the inequality
and the inequality

we obtain

If  then by (3.3), for
then by (3.3), for  , we obtain
, we obtain

Thus, combining (4.9), (4.12)–(4.13), (4.16)–(4.18), (4.21), and (4.10) or (4.11), we obtain that

Necessity.
We follow the method adopted by  . Tikhonov [15]. Note that if
. Tikhonov [15]. Note that if  , then
, then  . Integrating
. Integrating  , we have
, we have

and consequently

If  , then using (4.24),
, then using (4.24),

Using this and (3.3), for  , we obtain
, we obtain

Defining  we get
we get

and by (3.3), for  , we obtain
, we obtain

Applying Hölder's inequality, for  we have
we have

Finally,

which completes the proof.
4.3. Proof of Theorem 2.3
The proof of Theorem 2.3 goes analogously as the proof of Theorem 2.2. The only difference is that instead of (4.13) (for  ) and (4.18) (for
) and (4.18) (for  ) we use the below estimations.
) we use the below estimations.
Applying the inequalities  for
for  ,
,  for
for  and using (3.3), for
and using (3.3), for  we have
we have

This ends our proof.
4.4. Proof of Theorem 2.5
We prove the theorem for the case when  . The case when
. The case when  can be proved similarly.
can be proved similarly.
If  then by (2.3) we obtain that (2.7) obviously holds. Let
then by (2.3) we obtain that (2.7) obviously holds. Let  . It is clear that if
. It is clear that if  is an odd number, then
is an odd number, then

(for  the last sum should be omitted), and if
the last sum should be omitted), and if  is an even number, then
is an even number, then

Let

where  and
and  if
if  is an even number, and
is an even number, and  if
if  is an odd number.
is an odd number.
Then, for  , by (3.2) and (4.14), we get
, by (3.2) and (4.14), we get

We immediately have for 

If  and
and  , then by Hölder's inequality we have for
, then by Hölder's inequality we have for 

When  and
and  , an elementary calculation gives for
, an elementary calculation gives for 

If  , then
, then

We have

and taking  and
and  for
for  ,
,  for
for  in (3.3), we get for
in (3.3), we get for 

If  , then using (3.2) and (4.14), we have
, then using (3.2) and (4.14), we have

Set  ,
,  for
for  and
and  for
for  . Then by (3.3), we have for
. Then by (3.3), we have for 

Let

where  and
and 
 . Then, for
. Then, for  , using (3.2) and (4.19), we get
, using (3.2) and (4.19), we get

Therefore,

If  , then
, then

Similarly as in the estimation of the quantity  using (3.3) for
using (3.3) for  , we have
, we have

If  , then using (3.2) and (4.19), we have
, then using (3.2) and (4.19), we have

Further, by (3.3), we have for 

Combining (4.32) or (4.33), (4.35)–(4.43) and (4.45)–(4.50) we complete the proof of Theorem 2.5.
4.5. Proof of Theorem 2.6
The proof of Theorem 2.6 goes analogously as the proof of Theorem 2.5. The only difference is that instead of (4.41) (for  ) and (4.48) (for
) and (4.48) (for  ) we use the below estimations.
) we use the below estimations.
Applying the inequalities  for
for  and
and  for
for  and using (3.3), for
and using (3.3), for  we have
we have

This completes the proof.
References
Heywood P: On the integrability of functions defined by trigonometric series. The Quarterly Journal of Mathematics 1954, 5: 71–76. 10.1093/qmath/5.1.71
Chen Y-M: On the integrability of functions defined by trigonometrical series. Mathematische Zeitschrift 1956, 66: 9–12. 10.1007/BF01186590
Zygmund A: Trigonometric Series. Cambridge University Press, Cambridge, Mass, USA; 1977.
Boas RP Jr.: Integrability Theorems for Trigonometric Transforms, Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 38. Springer, New York, NY, USA; 1967:v+66.
Askey R, Wainger S: Integrability theorems for Fourier series. Duke Mathematical Journal 1966, 33: 223–228. 10.1215/S0012-7094-66-03326-6
Leindler L: A new class of numerical sequences and its applications to sine and cosine series. Analysis Mathematica 2002, 28(4):279–286. 10.1023/A:1021717700626
Tikhonov SYu: On the integrability of trigonometric series. Matematicheskie Zametki 2005, 78(3–4):437–442.
Tikhonov S: Trigonometric series with general monotone coefficients. Journal of Mathematical Analysis and Applications 2007, 326(1):721–735. 10.1016/j.jmaa.2006.02.053
Yu DS, Zhou P, Zhou SP: On integrability and convergence of trigonometric series. Studia Mathematica 2007, 182(3):215–226. 10.4064/sm182-3-3
Tikhonov S: Trigonometric series of Nikol'skii classes. Acta Mathematica Hungarica 2007, 114(1–2):61–78. 10.1007/s10474-006-0513-y
Tikhonov S: Best approximation and moduli of smoothness: computation and equivalence theorems. Journal of Approximation Theory 2008, 153(1):19–39. 10.1016/j.jat.2007.05.006
Le RJ, Zhou SP: A new condition for the uniform convergence of certain trigonometric series. Acta Mathematica Hungarica 2005, 108(1–2):161–169. 10.1007/s10474-005-0217-8
Leindler L: Embedding results regarding strong approximation of sine series. Acta Scientiarum Mathematicarum 2005, 71(1–2):91–103.
You DS, Zhou P, Zhou SP: Ultimate generalization to monotonicity for uniform convergence of trigonometric series. preprint, http://arxiv.org/abs/math/0611805
Dyachenko M, Tikhonov S: Integrability and continuity of functions represented by trigonometric series: coefficients criteria. Studia Mathematica 2009, 193(3):285–306. 10.4064/sm193-3-5
Wei B, Yu D: On weighted integrability and approximation of trigonometric series. Analysis in Theory and Applications 2009, 25(1):40–54. 10.1007/s10496-009-0040-0
Konyushkov AA: Best approximation by trigonometric polynomials and Fourier coefficients. Sbornik Mathematics 1958, 44: 53–84.
Leindler L: Best approximation and Fourier coefficients. Analysis Mathematica 2005, 31(2):117–129. 10.1007/s10476-005-0008-z
Szal B: On -convergence of trigonometric series. to appear, http://arxiv.org/abs/0908.4578
Leindler L: Generalization of inequalities of Hardy and Littlewood. Acta Scientiarum Mathematicarum 1970, 31: 279–285.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Szal, B. On Weighted 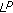 Integrability of Functions Defined by Trigonometric Series.
J Inequal Appl 2010, 485705 (2010). https://doi.org/10.1155/2010/485705
Integrability of Functions Defined by Trigonometric Series.
J Inequal Appl 2010, 485705 (2010). https://doi.org/10.1155/2010/485705
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/485705
 -Integrability
-Integrability ,
,
 ,
,  and
and  . If
. If  , then for all
, then for all 

 ,
,  and
and  , then
, then