- Research Article
- Open access
- Published:
Upper Semicontinuity of Solution Maps for a Parametric Weak Vector Variational Inequality
Journal of Inequalities and Applications volume 2010, Article number: 482726 (2010)
Abstract
This paper investigates the upper semicontinuity of the solution map for a parametric weak vector variational inequality associated to a  -hemicontinuous and weakly
-hemicontinuous and weakly  -pseudomonotone operator.
-pseudomonotone operator.
1. Introduction and Preliminaries
A vector variational inequality (VVI, in short) was first introduced by Giannessi [1] in the setting of finite-dimensional Euclidean space. Later on, it was studied and generalized to infinite-dimensional spaces. Existences of the solutions for VVI have been studied extensively in various versions; see [2–6] and references therein.
Stability of the solution map for VVI or vector equilibrium problems is an important topic in optimization theory. A great deal of papers have been denoted to study the semicontinuity and continuity of the solution maps; see [7–18] and references therein. All results of the stability of the solution map for VVI in the literature are obtained based on continuity of the operator. It is well known that  -hemicontinuity is weaker than continuity. In this paper, our aim is to investigate the upper semicontinuity of the solution map for a parametric weak vector variational inequality associated to a
-hemicontinuity is weaker than continuity. In this paper, our aim is to investigate the upper semicontinuity of the solution map for a parametric weak vector variational inequality associated to a  -hemicontinuous and weakly
-hemicontinuous and weakly  -pseudomonotone operator.
-pseudomonotone operator.
Let  ,
,  , and
, and  (the spaces of parameters) be Banach spaces and let
(the spaces of parameters) be Banach spaces and let  be a pointed closed and convex cone with nonempty interior
be a pointed closed and convex cone with nonempty interior  . Let
. Let  be the space of all linear continuous operators from
be the space of all linear continuous operators from  to
to  . The value of a linear operator
. The value of a linear operator  at
at  is denoted by
is denoted by  . Consider the following weak vector variational inequality problem:
. Consider the following weak vector variational inequality problem:

where  is a nonempty subset and
is a nonempty subset and  is a vector-valued mapping.
is a vector-valued mapping.
When  is perturbed by a parameter
is perturbed by a parameter  , which varies over a nonempty set
, which varies over a nonempty set  , for a given
, for a given  , we can define the parametric weak vector variational inequality problem
, we can define the parametric weak vector variational inequality problem

where  is a nonempty subset and
is a nonempty subset and  is a vector-valued mapping.
is a vector-valued mapping.
For each  , we denote the solution map of (PWVVI) by
, we denote the solution map of (PWVVI) by  , that is,
, that is,

Throughout the paper, we always assume that  is nonempty for all
is nonempty for all  in a neighborhood of
in a neighborhood of  . Now, we recall some basic definitions and their properties.
. Now, we recall some basic definitions and their properties.
Let  be a nonempty convex subset of
be a nonempty convex subset of  and let
and let  be an operator.
be an operator.  is said to be
is said to be  -hemicontinuous if and only if, for every
-hemicontinuous if and only if, for every  ,
,  and
and  , the mapping
, the mapping  is continuous at
is continuous at  .
.
Definition 1.2 (see [6]).
Let  be a nonempty subset of
be a nonempty subset of  and
and  be an operator.
be an operator.  is weakly
is weakly  -pseudomonotone on
-pseudomonotone on  if, for every pair of points
if, for every pair of points  ,
,  , one has that
, one has that  implies that
implies that  .
.
Proposition 1.3 (see [6, Generalized Linearization Lemma]).
Let  be a nonempty convex subset of
be a nonempty convex subset of  and let
and let  be an operator. Consider the following problems:
be an operator. Consider the following problems:
(I) such that
such that  for all
for all  ,
,
(II) such that
such that  for all
for all  .
.
Then the following are obtained.
(i)Problem (I) implies Problem (II) if  is weakly
is weakly  -pseudomonotone.
-pseudomonotone.
(ii)Problem (II) implies Problem (I) if  is
is  -hemicontinuous.
-hemicontinuous.
Let  be a set-valued mapping, given that
be a set-valued mapping, given that  .
.
Definition 1.4 (see [19, 20]).
(i) is called lower semicontinuous (l.s.c) at
is called lower semicontinuous (l.s.c) at  if, for any open set
if, for any open set  satisfying
satisfying  , there exists
, there exists  such that for every
such that for every  ,
,  .
.
(ii) is called upper semicontinuous (u.s.c) at
is called upper semicontinuous (u.s.c) at  if, for any open set
if, for any open set  satisfying
satisfying  , there exists
, there exists  such that, for every
such that, for every  ,
,  .
.
We say  is l.s.c (resp., u.s.c) on
is l.s.c (resp., u.s.c) on  , if it is l.s.c (resp., u.s.c) at each
, if it is l.s.c (resp., u.s.c) at each  .
.  is said to be continuous on
is said to be continuous on  if it is both l.s.c and u.s.c on
if it is both l.s.c and u.s.c on  .
.
Proposition 1.5 (see [19, 21]).
(i) is l.s.c at
is l.s.c at  if and only if, for any sequence
if and only if, for any sequence  with
with  and any
and any  , there exists
, there exists  such that
such that  .
.
-
(ii)
If
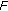 has compact values (i.e.,
has compact values (i.e., 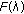 is a compact set for each
is a compact set for each  ), then
), then 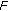 is u.s.c at
is u.s.c at 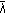 if and only if, for any sequence
if and only if, for any sequence 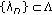 with
with 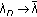 and for any
and for any 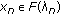 , there exist
, there exist 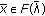 and a subsequence
and a subsequence  of
of 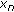 such that
such that  .
.
2. Main Results
In this section, we mainly discuss the upper semicontinuity of the solution map for (PWVVI).
Lemma 2.1.
Let  be a nonempty compact convex subset of
be a nonempty compact convex subset of  . Suppose that, for any
. Suppose that, for any  ,
,  is
is  -hemicontinuous and weakly
-hemicontinuous and weakly  -pseudomonotone on
-pseudomonotone on  . Then,
. Then,  has compact values on
has compact values on  , that is,
, that is,  is a compact set for each
is a compact set for each  .
.
Proof.
For any  , take any sequence
, take any sequence  with
with  ; we have
; we have

By Proposition 1.3 and the weakly  -pseudomonotonicity of
-pseudomonotonicity of  , we get
, we get

From  , we have
, we have  as
as  . It follows from the closedness of
. It follows from the closedness of  and (2.2) that
and (2.2) that

Moreover, by Proposition 1.3 and the  -hemicontinuity of
-hemicontinuity of  , we have
, we have

That is  . Thus,
. Thus,  is a closed set. Furthermore, it follows from
is a closed set. Furthermore, it follows from  and the compactness of
and the compactness of  that
that  is a compact set. The proof is complete.
is a compact set. The proof is complete.
Theorem 2.2.
Let  be a nonempty compact convex subset of
be a nonempty compact convex subset of  . Suppose that the following conditions are satisfied.
. Suppose that the following conditions are satisfied.
(i)For any  ,
,  is
is  -hemicontinuous on
-hemicontinuous on  ,
,
(ii)For any  ,
,  is weakly
is weakly  -pseudomonotone on
-pseudomonotone on  ,
,
(iii)For any  ,
,  is continuous on
is continuous on  .
.
Then,  is u.s.c on
is u.s.c on  .
.
Proof.
For any  , any sequences
, any sequences  with
with  , and
, and  , we have
, we have  and
and

Since  is a compact set, there are an
is a compact set, there are an  and a subsequence
and a subsequence  such that
such that  . Particularly, from (2.5), we get
. Particularly, from (2.5), we get

By Proposition 1.3 and (iii), we can obtain that

Since  is continuous and
is continuous and

we get  , as
, as  . It follows from the closedness of
. It follows from the closedness of  and (2.7) that
and (2.7) that

Moreover, by Proposition 1.3 and (ii), we have

that is  .
.
Thus, for any sequence  with
with  and for any
and for any  , there exist
, there exist  and a subsequence
and a subsequence  of
of  such that
such that  . By Proposition 1.5 and Lemma 2.1, we have
. By Proposition 1.5 and Lemma 2.1, we have  is u.s.c at
is u.s.c at  . From the arbitrariness of
. From the arbitrariness of  , we can get
, we can get  is u.s.c on
is u.s.c on  . The proof is complete.
. The proof is complete.
Remark 2.3.
In [7–10], the upper semicontinuity of the solution map for  has been discussed based on the continuity of the operator. Note that
has been discussed based on the continuity of the operator. Note that  -hemicontinuity is weaker than continuity. Moreover, together with the assumption of weakly
-hemicontinuity is weaker than continuity. Moreover, together with the assumption of weakly  -pseudomonotonicity,
-pseudomonotonicity,  -hemicontinuity may not derive the continuity of the operator. Thus, it is necessary to investigate the upper semicontinuity of the solution map for
-hemicontinuity may not derive the continuity of the operator. Thus, it is necessary to investigate the upper semicontinuity of the solution map for  associated to a
associated to a  -hemicontinuous and weakly
-hemicontinuous and weakly  -pseudomonotone operator. Now we give an example to illustrate our result.
-pseudomonotone operator. Now we give an example to illustrate our result.
Example 2.4.
Let  ,
,  ,
,  ,
,  and
and

Then,

It is clear that conditions (ii) and (iii) of Theorem 2.2 are satisfied. For any ray  ,
,  is continuous. Thus,
is continuous. Thus,  is
is  -hemicontinuous on
-hemicontinuous on  and condition (i) of Theorem 2.2 is satisfied. By Theorem 2.2, we conclude that
and condition (i) of Theorem 2.2 is satisfied. By Theorem 2.2, we conclude that  is u.s.c on
is u.s.c on  . In fact,
. In fact,

Then, by the definition of upper semicontinuity, it follows readily that the solutions map  is u.s.c on
is u.s.c on  .
.
However, for  with
with  , we have
, we have  , but
, but  . Thus, for any
. Thus, for any  ,
,  is not continuous at
is not continuous at  . Therefore, the theorems concerning the upper semicontinuity in the literatures are not applicable.
. Therefore, the theorems concerning the upper semicontinuity in the literatures are not applicable.
References
Giannessi F: Theorems of alternative, quadratic programs and complementarity problems. In Variational Inequalities and Complementarity Problems. Edited by: Cottle RW, Giannessi F, Lions JL. John Wiley & Sons, New York, NY, USA; 1980:151–186.
Chang S-S, Lee BS, Chen Y-Q: Variational inequalities for monotone operators in nonreflexive Banach spaces. Applied Mathematics Letters 1995, 8(6):29–34. 10.1016/0893-9659(95)00081-Z
Chen GY: Existence of solutions for a vector variational inequality: an extension of the Hartmann-Stampacchia theorem. Journal of Optimization Theory and Applications 1992, 74(3):445–456. 10.1007/BF00940320
Huang N-J, Fang Y-P: On vector variational inequalities in reflexive Banach spaces. Journal of Global Optimization 2005, 32(4):495–505. 10.1007/s10898-003-2686-z
Lee B-S, Lee G-M: Variational inequalities for -pseudomonotone operators in nonreflexive Banach spaces. Applied Mathematics Letters 1999, 12(5):13–17. 10.1016/S0893-9659(99)00050-6
Yu SJ, Yao JC: On vector variational inequalities. Journal of Optimization Theory and Applications 1996, 89(3):749–769. 10.1007/BF02275358
Cheng YH, Zhu DL: Global stability results for the weak vector variational inequality. Journal of Global Optimization 2005, 32(4):543–550. 10.1007/s10898-004-2692-9
Li SJ, Chen CR: Stability of weak vector variational inequality. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(4):1528–1535. 10.1016/j.na.2008.02.032
Li SJ, Chen GY, Teo KL: On the stability of generalized vector quasivariational inequality problems. Journal of Optimization Theory and Applications 2002, 113(2):283–295. 10.1023/A:1014830925232
Khanh PQ, Luu LM: Lower semicontinuity and upper semicontinuity of the solution sets and approximate solution sets of parametric multivalued quasivariational inequalities. Journal of Optimization Theory and Applications 2007, 133(3):329–339. 10.1007/s10957-007-9190-4
Chuong TD, Yao JC, Yen ND: Further results on the lower semicontinuity of efficient point multifunctions. Pacific Journal of Optimization 2010, 6: 405–422.
Chuong TD, Huy NQ, Yao JC: Stability of semi-infinite vector optimization problems under functional perturbations. Journal of Global Optimization 2009, 45(4):583–595. 10.1007/s10898-008-9391-x
Chuong TD, Huy NQ, Yao JC: Pseudo-Lipschitz property of linear semi-infinite vector optimization problems. European Journal of Operational Research 2010, 200(3):639–644. 10.1016/j.ejor.2009.01.004
Gong XH, Kimura K, Yao J-C: Sensitivity analysis of strong vector equilibrium problems. Journal of Nonlinear and Convex Analysis 2008, 9(1):83–94.
Kimura K, Yao JC: Semicontinuity of solution mappings of parametric generalized vector equilibrium problems. Journal of Optimization Theory and Applications 2008, 138(3):429–443. 10.1007/s10957-008-9386-2
Kimura K, Yao J-C: Semicontinuity of solution mappings of parametric generalized strong vector equilibrium problems. Journal of Industrial and Management Optimization 2008, 4(1):167–181.
Kimura K, Yao J-C: Sensitivity analysis of solution mappings of parametric vector quasi-equilibrium problems. Journal of Global Optimization 2008, 41(2):187–202. 10.1007/s10898-007-9210-9
Kimura K, Yao J-C: Sensitivity analysis of solution mappings of parametric generalized quasi vector equilibrium problems. Taiwanese Journal of Mathematics 2008, 12(9):2233–2268.
Aubin J-P, Ekeland I: Applied Nonlinear Analysis, Pure and Applied Mathematics. John Wiley & Sons, New York, NY, USA; 1984:xi+518.
Kien BT: On the lower semicontinuity of optimal solution sets. Optimization 2005, 54(2):123–130. 10.1080/02331930412331330379
Ferro F: A minimax theorem for vector-valued functions. Journal of Optimization Theory and Applications 1989, 60(1):19–31. 10.1007/BF00938796
Acknowledgments
The authors would like to thank two anonymous referees for their valuable comments and suggestions, which helped to improve the paper. This research was partially supported by the National Natural Science Foundation of China (Grant no. 10871216) and Chongqing University Postgraduates Science and Innovation Fund (Project no. 201005B1A0010338).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Fang, Z., Li, S. Upper Semicontinuity of Solution Maps for a Parametric Weak Vector Variational Inequality. J Inequal Appl 2010, 482726 (2010). https://doi.org/10.1155/2010/482726
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/482726
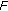 has compact values (i.e.,
has compact values (i.e., 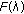 is a compact set for each
is a compact set for each  ), then
), then 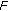 is u.s.c at
is u.s.c at 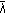 if and only if, for any sequence
if and only if, for any sequence 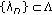 with
with 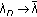 and for any
and for any 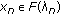 , there exist
, there exist 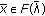 and a subsequence
and a subsequence  of
of 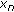 such that
such that  .
.