- Research Article
- Open access
- Published:
Note on  -Nasybullin's Lemma Associated with the Modified
-Nasybullin's Lemma Associated with the Modified 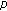 -Adic
-Adic 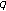 -Euler Measure
-Euler Measure
Journal of Inequalities and Applications volume 2010, Article number: 482717 (2010)
Abstract
We derive the modified  -adic
-adic  -measures related to
-measures related to  -Nasybullin's type lemma.
-Nasybullin's type lemma.
1. Introduction
Let  be a fixed prime number. Throughout this paper, the symbols
be a fixed prime number. Throughout this paper, the symbols  ,
,  ,
,  , and
, and  denote the ring of rational integers, the ring of
denote the ring of rational integers, the ring of  -adic rational integers, the field of
-adic rational integers, the field of  -adic rational numbers, and the completion of algebraic closure of
-adic rational numbers, and the completion of algebraic closure of  , respectively. Let
, respectively. Let  be the set of natural numbers and
be the set of natural numbers and  . The
. The  -adic absolute value in
-adic absolute value in  is normalized in such a way that
is normalized in such a way that  (see [1–17]). For
(see [1–17]). For  with
with  , let
, let  be the least common multiple of
be the least common multiple of  and
and  . We set
. We set

where  lies in
lies in  .
.
When one talks of  -extension,
-extension,  is variously considered as an indeterminate, a complex number
is variously considered as an indeterminate, a complex number  or a
or a  -adic number
-adic number  . In this paper, we assume that
. In this paper, we assume that  with
with  (see [1–6, 18–23]). As the definition of
(see [1–6, 18–23]). As the definition of  -number, we use the following notations:
-number, we use the following notations:

Let  be the space of uniformly differentiable function on
be the space of uniformly differentiable function on  . For
. For  , the
, the  -adic
-adic  -invariant integral on
-invariant integral on  is defined as
is defined as

The  -Euler numbers,
-Euler numbers,  , can be determined inductively by
, can be determined inductively by

with the usual convention of replacing  by
by  (see [11]). The modified
(see [11]). The modified  -Euler numbers
-Euler numbers  of
of  are defined in [2] as follows:
are defined in [2] as follows:

with the usual convention of replacing  by
by  . For any positive integer
. For any positive integer  ,
,

is known as a measure on  (see [9]). In [2], the Witt's type formulas for
(see [9]). In [2], the Witt's type formulas for  are given by
are given by

The modified  -Euler polynomials are also defined by
-Euler polynomials are also defined by

with the usual convention of replacing  by
by  (see [2]). Thus, we note that
(see [2]). Thus, we note that

Recently Govil and Gupta [22] have introduced a new type of q-integrated Meyer-König-Zeller-Durrmeyer (q-MKZD) operators, obtained moments for these operators, and estimated the convergence of these integrated q-MKZD operators. In this paper, we consider the q-extension which is in a direction different than that of Govil and Gupta [22].
Let  be a field over
be a field over  . Then we call a function
. Then we call a function  a
a  -measure on
-measure on  if
if  is finitely additive function defined on open-closed subsets in
is finitely additive function defined on open-closed subsets in  , whose values are in the field
, whose values are in the field  . Any open-closed subset in
. Any open-closed subset in  is a disjoint union of some finite intervals
is a disjoint union of some finite intervals  in
in  , where
, where  is prime to
is prime to  , and therefore a
, and therefore a  -measure
-measure  is determined by its values on all intervals in
is determined by its values on all intervals in  . Let
. Let  denote the set of all rational numbers, whose denominator is a divisor of
denote the set of all rational numbers, whose denominator is a divisor of  for some
for some  . In Section 2, we derive the modified
. In Section 2, we derive the modified  -adic
-adic  -measures related to
-measures related to  -Nasybullin's type lemma.
-Nasybullin's type lemma.
2. The Modified 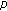 -Adic
-Adic 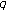 -Measure
-Measure
Let  be a
be a  -valued function defined on
-valued function defined on  with the following property.
with the following property.
There exist two constants  such that
such that

for any number  . Suppose that
. Suppose that  is a root of the equation
is a root of the equation  . Then we define
. Then we define

for any interval  . From (2.2), we note that
. From (2.2), we note that

Thus, we have

Therefore we obtain the following theorem.
Theorem 2.1.
For  with
with  and
and  , let
, let  be a
be a  -valued function defined on
-valued function defined on  with the following properties.
with the following properties.
There exist two constants  such that
such that

for any  . Suppose that
. Suppose that  is a root of the equation
is a root of the equation  . Then there exists a
. Then there exists a  -measure
-measure  on
on  such that
such that

for any interval  .
.
From (1.9), we note that

Let  be the
be the  th
th  -Euler polynomials and let
-Euler polynomials and let  be the
be the  th
th  -Euler functions, that is, for
-Euler functions, that is, for  ,
,

Note that  is the Euler function. By (2.7), we see that
is the Euler function. By (2.7), we see that

Thus, the  -Euler function
-Euler function  satisfies the properties of Theorem 2.1 with constants
satisfies the properties of Theorem 2.1 with constants

Then  is equal to
is equal to  , as
, as  reduces simply to
reduces simply to  . Therefore, we obtain the following theorem.
. Therefore, we obtain the following theorem.
Theorem 2.2.
For  , let the function
, let the function  be defined on
be defined on  as follows:
as follows:

Then  is a
is a  -measure on
-measure on  .
.
For  with
with  and
and  , let
, let  be a primitive Dirichlet character modulo
be a primitive Dirichlet character modulo  . Then the generalized
. Then the generalized  -Euler numbers are defined as follows:
-Euler numbers are defined as follows:

From (2.12) and (2.7), we can easily derive the following Witt's formula:

We can compute a  -analogue of the
-analogue of the  -adic
-adic  -
- -function by the following
-function by the following  -adic
-adic  -Mellin Mazur transform with respect to
-Mellin Mazur transform with respect to  .
.
Let

Since the character  is constant on the interval
is constant on the interval  ,
,

where  are the
are the  th generalized
th generalized  -Euler numbers attached to
-Euler numbers attached to  . For
. For  , we have
, we have

Assume that  with
with  . Let
. Let  be the Teichmüller character mod
be the Teichmüller character mod  . For
. For  , we set
, we set  . Note that
. Note that  and
and  are defined by
are defined by  for
for  . For
. For  , we define
, we define

For (2.14), (2.16) and (2.17), we note that

Since  for
for  , we have
, we have  . Let
. Let  . Then we have
. Then we have

Therefore, we obtain the following theorem.
Theorem 2.3.
For  , we have
, we have

References
Jang L-C: A study on the distribution of twisted -Genocchi polynomials. Advanced Studies in Contemporary Mathematics 2009, 18(2):181–189.
Kim T: The modified -Euler numbers and polynomials. Advanced Studies in Contemporary Mathematics 2008, 16(2):161–170.
Kim T: Symmetry of power sum polynomials and multivariate fermionic -adic invariant integral on . Russian Journal of Mathematical Physics 2009, 16(1):93–96. 10.1134/S1061920809010063
Kim T: -Volkenborn integration. Russian Journal of Mathematical Physics 2002, 9(3):288–299.
Kim T: On Euler-Barnes multiple zeta functions. Russian Journal of Mathematical Physics 2003, 10(3):261–267.
Kim T: Non-Archimedean -integrals associated with multiple Changhee -Bernoulli polynomials. Russian Journal of Mathematical Physics 2003, 10(1):91–98.
Kim T: Power series and asymptotic series associated with the -analog of the two-variable -adic -function. Russian Journal of Mathematical Physics 2005, 12(2):186–196.
Kim T: -generalized Euler numbers and polynomials. Russian Journal of Mathematical Physics 2006, 13(3):293–298. 10.1134/S1061920806030058
Kim T: -Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008, 15(1):51–57.
Kim T: A note on the generalized -Euler numbers. Proceedings of the Jangjeon Mathematical Society 2009, 12(1):45–50.
Kim T, Hwang K-W, Lee B: A note on the -Euler measures. Advances in Difference Equations 2009, 2009:-8.
Kim T: Note on the Euler -zeta functions. Journal of Number Theory 2009, 129(7):1798–1804. 10.1016/j.jnt.2008.10.007
Kim T: On a -analogue of the -adic log gamma functions and related integrals. Journal of Number Theory 1999, 76(2):320–329. 10.1006/jnth.1999.2373
Kim Y-H, Kim W, Ryoo CS: On the twisted -Euler zeta function associated with twisted -Euler numbers. Proceedings of the Jangjeon Mathematical Society 2009, 12(1):93–100.
Ozden H, Cangul IN, Simsek Y: Remarks on -Bernoulli numbers associated with Daehee numbers. Advanced Studies in Contemporary Mathematics 2009, 18(1):41–48.
Ozden H, Simsek Y, Rim S-H, Cangul IN: A note on -adic -Euler measure. Advanced Studies in Contemporary Mathematics 2007, 14(2):233–239.
Rim S-H, Kim T: A note on -adic Euler measure on . Russian Journal of Mathematical Physics 2006, 13(3):358–361. 10.1134/S1061920806030113
Carlitz L: -Bernoulli numbers and polynomials. Duke Mathematical Journal 1948, 15: 987–1000. 10.1215/S0012-7094-48-01588-9
Cangul IN, Kurt V, Ozden H, Simsek Y: On the higher-order --Genocchi numbers. Advanced Studies in Contemporary Mathematics 2009, 19(1):39–57.
Cenkci M: The -adic generalized twisted -Euler--function and its applications. Advanced Studies in Contemporary Mathematics 2007, 15(1):37–47.
Can M, Cenkci M, Kurt V, Simsek Y: Twisted Dedekind type sums associated with Barnes' type multiple Frobenius-Euler -functions. Advanced Studies in Contemporary Mathematics 2009, 18(2):135–160.
Govil NK, Gupta V: Convergence of -Meyer-König-Zeller-Durrmeyer operators. Advanced Studies in Contemporary Mathematics 2009, 19(1):97–108.
Gupta V, Finta Z: On certain -Durrmeyer type operators. Applied Mathematics and Computation 2009, 209(2):415–420. 10.1016/j.amc.2008.12.071
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kim, T., Kim, YH., Jang, LC. et al. Note on  -Nasybullin's Lemma Associated with the Modified
-Nasybullin's Lemma Associated with the Modified 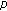 -Adic
-Adic 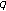 -Euler Measure.
J Inequal Appl 2010, 482717 (2010). https://doi.org/10.1155/2010/482717
-Euler Measure.
J Inequal Appl 2010, 482717 (2010). https://doi.org/10.1155/2010/482717
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/482717
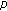 -Adic
-Adic 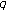 -Measure
-Measure