- Research Article
- Open access
- Published:
On Some New Sequence Spaces in 2-Normed Spaces Using Ideal Convergence and an Orlicz Function
Journal of Inequalities and Applications volume 2010, Article number: 482392 (2010)
Abstract
The purpose of this paper is to introduce certain new sequence spaces using ideal convergence and an Orlicz function in 2-normed spaces and examine some of their properties.
1. Introduction
The notion of ideal convergence was introduced first by Kostyrko et al. [1] as a generalization of statistical convergence which was further studied in topological spaces [2]. More applications of ideals can be seen in [3, 4].
The concept of 2-normed space was initially introduced by Gähler [5] as an interesting nonlinear generalization of a normed linear space which was subsequently studied by many authors (see, [6, 7]). Recently, a lot of activities have started to study summability, sequence spaces and related topics in these nonlinear spaces (see, [8–10]).
Recall in [11] that an Orlicz function  is continuous, convex, nondecreasing function such that
is continuous, convex, nondecreasing function such that  and
and  for
for  , and
, and  as
as  .
.
Subsequently Orlicz function was used to define sequence spaces by Parashar and Choudhary [12] and others.
If convexity of Orlicz function,  is replaced by
is replaced by  , then this function is called Modulus function, which was presented and discussed by Ruckle [13] and Maddox [14].
, then this function is called Modulus function, which was presented and discussed by Ruckle [13] and Maddox [14].
Note that if  is an Orlicz function then
is an Orlicz function then  for all
for all  with
with 
Let  be a normed space. Recall that a sequence
be a normed space. Recall that a sequence  of elements of
of elements of  is called to be statistically convergent to
is called to be statistically convergent to  if the set
if the set  has natural density zero for each
has natural density zero for each  .
.
A family  of subsets a nonempty set
of subsets a nonempty set  is said to be an ideal in
is said to be an ideal in  if (i)
if (i)  (ii)
(ii)  imply
imply  (iii)
(iii) 
 imply
imply  , while an admissible ideal
, while an admissible ideal  of
of  further satisfies
further satisfies  for each
for each  , [9, 10].
, [9, 10].
Given  is a nontrivial ideal in
is a nontrivial ideal in  . The sequence
. The sequence  in
in  is said to be
is said to be  -convergent to
-convergent to  if for each
if for each  the set
the set  belongs to
belongs to  , [1, 3].
, [1, 3].
Let  be a real vector space of dimension
be a real vector space of dimension  where
where  A 2-norm on
A 2-norm on  is a function
is a function  which satisfies (i)
which satisfies (i)  if and only if
if and only if  and
and  are linearly dependent, (ii)
are linearly dependent, (ii)  , (iii)
, (iii) 
 , and (iv)
, and (iv)  . The pair
. The pair  is then called a
is then called a  -normed space [6].
-normed space [6].
Recall that  is a 2-Banach space if every Cauchy sequence in
is a 2-Banach space if every Cauchy sequence in  is convergent to some
is convergent to some  in
in 
Quite recently Savaş [15] defined some sequence spaces by using Orlicz function and ideals in 2-normed spaces.
In this paper, we continue to study certain new sequence spaces by using Orlicz function and ideals in 2-normed spaces. In this context it should be noted that though sequence spaces have been studied before they have not been studied in nonlinear structures like  -normed spaces and their ideals were not used.
-normed spaces and their ideals were not used.
2. Main Results
Let  be a nondecreasing sequence of positive numbers tending to
be a nondecreasing sequence of positive numbers tending to  such that
such that  and let
and let  be an admissible ideal of
be an admissible ideal of  , let
, let  be an Orlicz function, and let
be an Orlicz function, and let  be a 2-normed space. Further, let
be a 2-normed space. Further, let  be a bounded sequence of positive real numbers. By
be a bounded sequence of positive real numbers. By  we denote the space of all sequences defined over
we denote the space of all sequences defined over  . Now, we define the following sequence spaces:
. Now, we define the following sequence spaces:

where 
The following well-known inequality [16, page 190] will be used in the study.
[16, page 190] will be used in the study.

then

for all  and
and  . Also
. Also  for all
for all  .
.
Theorem 2.1.

are linear spaces.
Proof.
We will prove the assertion for  only and the others can be proved similarly. Assume that
only and the others can be proved similarly. Assume that 
 and
and  , so
, so

Since  is a 2-norm, and
is a 2-norm, and  is an Orlicz function the following inequality holds:
is an Orlicz function the following inequality holds:

where

From the above inequality, we get

Two sets on the right hand side belong to  and this completes the proof.
and this completes the proof.
It is also easy to see that the space  is also a linear space and we now have the following.
is also a linear space and we now have the following.
Theorem 2.2.
For any fixed  ,
,  is paranormed space with respect to the paranorm defined by
is paranormed space with respect to the paranorm defined by

Proof.
That  and
and  are easy to prove. So we omit them.
are easy to prove. So we omit them.
-
(iii)
Let us take
 and
and 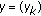 in
in  . Let
. Let  (2.9)
(2.9)
Let  and
and  , then if
, then if  , then, we have
, then, we have

Thus,  and
and

(iv) Finally using the same technique of Theorem  of Savaş [15] it can be easily seen that scalar multiplication is continuous. This completes the proof.
of Savaş [15] it can be easily seen that scalar multiplication is continuous. This completes the proof.
Corollary 2.3.
It should be noted that for a fixed  the space
the space

which is a subspace of the space  is a paranormed space with the paranorms
is a paranormed space with the paranorms  for
for  and
and  .
.
Theorem 2.4.
Let  ,
, be Orlicz functions. Then we have
be Orlicz functions. Then we have
(i) provided
provided  is such that
is such that  .
.
(ii) ⊆
⊆ .
.
Proof.
-
(i)
For given
 first choose
first choose 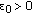 such that
such that 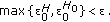 Now using the continuity of
Now using the continuity of 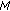 choose
choose 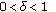 such that
such that 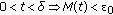 . Let
. Let 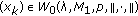 . Now from the definition
. Now from the definition  (2.13)
(2.13)
Thus if  then
then

that is,

that is,

that is,

Hence from above using the continuity of  we must have
we must have

which consequently implies that

that is,

This shows that

and so belongs to  . This proves the result.
. This proves the result.
-
(ii)
Let
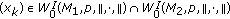 , then the fact
, then the fact  (2.22)
(2.22)
gives us the result.
Definition 2.5.
Let  be a sequence space. Then
be a sequence space. Then  is called solid if
is called solid if  whenever
whenever  for all sequences
for all sequences  of scalars with
of scalars with  for all
for all  .
.
Theorem 2.6.
The sequence spaces  are solid.
are solid.
Proof.
We give the proof for  only. Let
only. Let  and let
and let  be a sequence of scalars such that
be a sequence of scalars such that  for all
for all  . Then we have
. Then we have

where  . Hence
. Hence  for all sequences of scalars
for all sequences of scalars  with
with  for all
for all  whenever
whenever  .
.
References
Kostyrko P, Šalát T, Wilczyński W: -convergence. Real Analysis Exchange 2000, 26(2):669–686.
Lahiri BK, Das P: and -convergence in topological spaces. Mathematica Bohemica 2005, 130(2):153–160.
Kostyrko P, Mačaj M, Šalát T, Sleziak M: -convergence and extremal -limit points. Mathematica Slovaca 2005, 55(4):443–464.
Das P, Malik P: On the statistical and - variation of double sequences. Real Analysis Exchange 2008, 33(2):351–364.
Gähler S: 2-metrische Räume und ihre topologische Struktur. Mathematische Nachrichten 1963, 26: 115–148. 10.1002/mana.19630260109
Gunawan H, Mashadi : On finite-dimensional 2-normed spaces. Soochow Journal of Mathematics 2001, 27(3):321–329.
Freese RW, Cho YJ: Geometry of Linear 2-Normed Spaces. Nova Science, Hauppauge, NY, USA; 2001:viii+301.
Şahiner A, Gürdal M, Saltan S, Gunawan H: Ideal convergence in 2-normed spaces. Taiwanese Journal of Mathematics 2007, 11(5):1477–1484.
Gürdal M, Pehlivan S: Statistical convergence in 2-normed spaces. Southeast Asian Bulletin of Mathematics 2009, 33(2):257–264.
Gürdal M, Şahiner A, Açık I: Approximation theory in 2-Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2009, 71(5–6):1654–1661. 10.1016/j.na.2009.01.030
Krasnoselskii MA, Rutisky YB: Convex Function and Orlicz Spaces. Noordhoff, Groningen, The Netherlands; 1961.
Parashar SD, Choudhary B: Sequence spaces defined by Orlicz functions. Indian Journal of Pure and Applied Mathematics 1994, 25(4):419–428.
Ruckle WH: spaces in which the sequence of coordinate vectors is bounded. Canadian Journal of Mathematics 1973, 25: 973–978. 10.4153/CJM-1973-102-9
Maddox IJ: Sequence spaces defined by a modulus. Mathematical Proceedings of the Cambridge Philosophical Society 1986, 100(1):161–166. 10.1017/S0305004100065968
Savaş E: -strongly summable sequences spaces in 2-normed spaces defined by ideal convergence and an Orlicz function. Applied Mathematics and Computation 2010, 217(1):271–276. 10.1016/j.amc.2010.05.057
Maddox IJ: Elements of Functional Analysis. Cambridge University Press, London, UK; 1970:x+208.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Savaş, E. On Some New Sequence Spaces in 2-Normed Spaces Using Ideal Convergence and an Orlicz Function. J Inequal Appl 2010, 482392 (2010). https://doi.org/10.1155/2010/482392
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/482392
 and
and 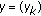 in
in  . Let
. Let 
 first choose
first choose 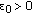 such that
such that 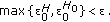 Now using the continuity of
Now using the continuity of 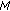 choose
choose 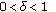 such that
such that 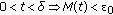 . Let
. Let 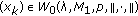 . Now from the definition
. Now from the definition 
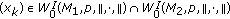 , then the fact
, then the fact 