- Research Article
- Open access
- Published:
Generalized Vector-Valued Sequence Spaces Defined by Modulus Functions
Journal of Inequalities and Applications volume 2010, Article number: 457892 (2010)
Abstract
We introduce the vector-valued sequence spaces  ,
,  , and
, and  ,
,  and
and  , using a sequence of modulus functions and the multiplier sequence
, using a sequence of modulus functions and the multiplier sequence  of nonzero complex numbers. We give some relations related to these sequence spaces. It is also shown that if a sequence is strongly
of nonzero complex numbers. We give some relations related to these sequence spaces. It is also shown that if a sequence is strongly  -Cesàro summable with respect to the modulus function
-Cesàro summable with respect to the modulus function  then it is
then it is  -statistically convergent.
-statistically convergent.
1. Introduction
Let  be the set of all sequences real or complex numbers and
be the set of all sequences real or complex numbers and  ,
,  , and
, and  be, respectively, the Banach spaces of bounded, convergent, and null sequences
be, respectively, the Banach spaces of bounded, convergent, and null sequences with the usual norm
with the usual norm  , where
, where  , the set of positive integers.
, the set of positive integers.
The studies on vector-valued sequence spaces are done by Das and Choudhury [1], Et [2], Et et al. [3], Leonard [4], Rath and Srivastava [5], J. K. Srivastava and B. K. Srivastava [6], Tripathy et al. [7, 8], and many others.
Let  be a sequence of seminormed spaces such that
be a sequence of seminormed spaces such that  for each
for each  . We define
. We define

It is easy to verify that  is a linear space under usual coordinatewise operations defined by
is a linear space under usual coordinatewise operations defined by  and
and  , where
, where  .
.
Let  be a sequences of nonzero scalar. Then for a sequence space
be a sequences of nonzero scalar. Then for a sequence space  , the multiplier sequence space
, the multiplier sequence space  , associated with the multiplier sequence
, associated with the multiplier sequence  , is defined as
, is defined as  .
.
The notion of a modulus was introduced by Nakano [9]. We recall that a modulus  is a function from
is a function from  to
to  such that
such that
(i) if and only if
if and only if  ,
,
(ii) for
for  ,
,
(iii) is increasing,
is increasing,
(iv) is continuous from the right at 0.
is continuous from the right at 0.
It follows that  must be continuous everywhere on
must be continuous everywhere on  . Maddox [10] and Ruckle [11] used a modulus function to construct some sequence spaces.
. Maddox [10] and Ruckle [11] used a modulus function to construct some sequence spaces.
After then some sequence spaces defined by a modulus function were introduced and studied by Bilgin [12], Pehlivan and Fisher [13], Waszak [14], Bhardwaj [15], Altın [16], and many others.
The notion of difference sequence spaces was introduced by Kızmaz [17] and it was generalized by Et and Çolak [18]. Let  be a fixed positive integer. Then we write
be a fixed positive integer. Then we write

for 
 ,
,  and
and  , where
, where  ,
,  ,
,  and so we have
and so we have

2. Main Results
In this section, we prove some results involving the sequence spaces  ,
,  , and
, and  .
.
Definition 2.1.
Let  be a sequence of seminormed spaces such that
be a sequence of seminormed spaces such that  for each
for each  ,
,  a sequence of strictly positive real numbers,
a sequence of strictly positive real numbers,  a sequence of seminorms,
a sequence of seminorms,  a sequence of modulus functions, and
a sequence of modulus functions, and  any fixed sequence of nonzero complex numbers
any fixed sequence of nonzero complex numbers  . We define the following sequence spaces:
. We define the following sequence spaces:

Throughout the paper  will denote any one of the notation 0,1 or
will denote any one of the notation 0,1 or  .
.
If 

 and
and  for all
for all  , we will write
, we will write  instead of
instead of  .
.
If  and
and  for all
for all  , we will write
, we will write  instead of
instead of  .
.
If  , we say that
, we say that  is strongly
is strongly  -Cesàro summable with respect to the modulus function
-Cesàro summable with respect to the modulus function  and we will write
and we will write  and
and  will be called
will be called  -limit of
-limit of  with respect to the modulus
with respect to the modulus  .
.
The proofs of the following theorems are obtained by using the known standard techniques; therefore, we give them without proofs.
Theorem 2.2.
Let the sequence  be bounded. Then the spaces
be bounded. Then the spaces  are linear spaces.
are linear spaces.
Theorem 2.3.
Let  be a modulus function and the sequence
be a modulus function and the sequence  be bounded; then
be bounded; then

and the inclusions are strict.
Theorem 2.4.

is a paranormed (need not total paranorm) space with

where  .
.
Theorem 2.5.
Let  and
and  be any two sequences of modulus functions. For any bounded sequences
be any two sequences of modulus functions. For any bounded sequences  and
and  of strictly positive real numbers and for any two sequences of seminorms
of strictly positive real numbers and for any two sequences of seminorms 
 and
and  , we have
, we have
(i) ;
;
(ii) ;
;
(iii) ;
;
(iv)If  is stronger than
is stronger than  for each
for each  , then
, then  ;
;
(v)If  equivalent to
equivalent to  for each
for each  , then
, then  ;
;
(vi) .
.
Proof.
-
(i)
We will only prove (i) for
 and the other cases can be proved by using similar arguments. Let
and the other cases can be proved by using similar arguments. Let  and choose
and choose 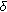 with
with  such that
such that 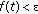 for
for 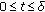 and for all
and for all  . Write
. Write 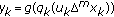 and consider
and consider 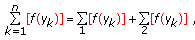 (2.4)
(2.4)
where the first summation is over  and second summation is over
and second summation is over  . Since
. Since  is continuous, we have
is continuous, we have

By the definition of  , we have for
, we have for  ,
,

Hence

From (2.5) and (2.7), we obtain  .
.
The following result is a consequence of Theorem 2.5(i).
Corollary 2.6.
Let  be a modulus function. Then
be a modulus function. Then  .
.
Theorem 2.7.
Let  and
and  be bounded; then
be bounded; then  .
.
Proof.
If we take  for all
for all  and using the same technique of Theorem 5 of Maddox [19], it is easy to prove the theorem.
and using the same technique of Theorem 5 of Maddox [19], it is easy to prove the theorem.
Theorem 2.8.
Let  be a modulus function; if
be a modulus function; if  , then
, then  .
.
Proof.
Omitted.
3. 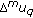 -Statistical Convergence
-Statistical Convergence
The notion of statistical convergence were introduced by Fast [20] and Schoenberg [21], independently. Over the years and under different names, statistical convergence has been discussed in the theory of Fourier analysis, ergodic theory, and number theory. Later on it was further investigated from the sequence space point of view and linked with summability theory by Šalát [22], Fridy [23], Connor [24], Mursaleen [25], Işik [26], Malkowsky and Sava [27], and many others. In recent years, generalizations of statistical convergence have appeared in the study of strong integral summability and the structure of ideals of bounded continuous functions on locally compact spaces. Statistical convergence and its generalizations are also connected with subsets of the Stone-Čech compactification of the natural numbers. Moreover, statistical convergence is closely related to the concept of convergence in probability. The notion depends on the density of subsets of the set
[27], and many others. In recent years, generalizations of statistical convergence have appeared in the study of strong integral summability and the structure of ideals of bounded continuous functions on locally compact spaces. Statistical convergence and its generalizations are also connected with subsets of the Stone-Čech compactification of the natural numbers. Moreover, statistical convergence is closely related to the concept of convergence in probability. The notion depends on the density of subsets of the set  of natural numbers.
of natural numbers.
A subset  of
of  is said to have density positive integers which is defined by
is said to have density positive integers which is defined by  if
if

where  is the characteristic function of
is the characteristic function of  . It is clear that any finite subset of
. It is clear that any finite subset of  have zero natural density and
have zero natural density and  .
.
In this section, we introduce  -statistically convergent sequences and give some inclusion relations between
-statistically convergent sequences and give some inclusion relations between  -statistically convergent sequences and
-statistically convergent sequences and  -summable sequences.
-summable sequences.
Definition 3.1.
A sequence  is said to be
is said to be  -statistically convergent to
-statistically convergent to  if for every
if for every  ,
,

In this case, we write  . The set of all
. The set of all  -statistically convergent sequences is denoted by
-statistically convergent sequences is denoted by  . In the case
. In the case  , we will write
, we will write 
 instead of
instead of  .
.
Theorem 3.2.
Let  be a modulus function; then
be a modulus function; then
(i)If  , then
, then  ;
;
(ii)If  and
and  , then
, then  ;
;
(iii) ,
,
where 

 .
.
Proof.
Omitted.
In the following theorems, we will assume that the sequence  is bounded and
is bounded and  .
.
Theorem 3.3.
Let  be a modulus function. Then
be a modulus function. Then  .
.
Proof.
Let  and let
and let  be given. Let
be given. Let  and
and  denote the sums over
denote the sums over  with
with  and
and  , respectively. Then
, respectively. Then

Hence  .
.
Theorem 3.4.
Let  be bounded; then
be bounded; then  .
.
Proof.
Suppose that  is bounded. Let
is bounded. Let  and
and  and
and  be denoted in previous theorem. Since
be denoted in previous theorem. Since  is bounded, there exists an integer
is bounded, there exists an integer  such that
such that  , for all
, for all  . Then
. Then

Hence  .
.
Theorem 3.5.

if and only if  is bounded.
is bounded.
Proof.
Let  be bounded. By Theorems 3.3 and 3.4, we have
be bounded. By Theorems 3.3 and 3.4, we have  .
.
Conversely suppose that  is unbounded. Then there exists a sequence
is unbounded. Then there exists a sequence  of positive numbers with
of positive numbers with  , for
, for  . If we choose
. If we choose

then we have

for all  and so
and so  , but
, but  for
for  ,
,  and
and  for all
for all  . This contradicts to
. This contradicts to  .
.
References
Das NR, Choudhury A: Matrix transformation of vector valued sequence spaces. Bulletin of the Calcutta Mathematical Society 1992, 84(1):47–54.
Et M: Spaces of Cesàro difference sequences of order r defined by a modulus function in a locally convex space. Taiwanese Journal of Mathematics 2006, 10(4):865–879.
Et M, Gökhan A, Altinok H: On statistical convergence of vector-valued sequences associated with multiplier sequences. Ukraïns'kiĭ Matematichniĭ Zhurnal 2006, 58(1):125–131. translation in Ukrainian Mathematical Journal, vol. 58, no. 1, pp. 139–146, 2006
Leonard IE: Banach sequence spaces. Journal of Mathematical Analysis and Applications 1976, 54(1):245–265. 10.1016/0022-247X(76)90248-1
Ratha A, Srivastava PD: On some vector valued sequence spaces . Ganita 1996, 47(1):1–12.
Srivastava JK, Srivastava BK: Generalized sequence space . Indian Journal of Pure and Applied Mathematics 1996, 27(1):73–84.
Tripathy BC, Sen M: Vector valued paranormed bounded and null sequence spaces associated with multiplier sequences. Soochow Journal of Mathematics 2003, 29(3):313–326.
Tripathy BC, Mahanta S: On a class of vector-valued sequences associated with multiplier sequences. Acta Mathematicae Applicatae Sinica. English Series 2004, 20(3):487–494. 10.1007/s10255-004-0186-7
Nakano H: Concave modulars. Journal of the Mathematical Society of Japan 1953, 5: 29–49. 10.2969/jmsj/00510029
Maddox IJ: Sequence spaces defined by a modulus. Mathematical Proceedings of the Cambridge Philosophical Society 1986, 100(1):161–166. 10.1017/S0305004100065968
Ruckle WH: FK spaces in which the sequence of coordinate vectors is bounded. Canadian Journal of Mathematics 1973, 25: 973–978. 10.4153/CJM-1973-102-9
Bilgin T: The sequence space ℓ(p,f,q,s) on seminormed spaces. Bulletin of the Calcutta Mathematical Society 1994, 86(4):295–304.
Pehlivan S, Fisher B: On some sequence spaces. Indian Journal of Pure and Applied Mathematics 1994, 25(10):1067–1071.
Waszak A: On the strong convergence in some sequence spaces. Fasciculi Mathematici 2002, (33):125–137.
Bhardwaj VK: A generalization of a sequence space of Ruckle. Bulletin of the Calcutta Mathematical Society 2003, 95(5):411–420.
Altın Y: Properties of some sets of sequences defined by a modulus function. Acta Mathematica Scientia B. English Edition 2009, 29(2):427–434.
Kızmaz H: On certain sequence spaces. Canadian Mathematical Bulletin 1981, 24(2):169–176. 10.4153/CMB-1981-027-5
Et M, Çolak R: On some generalized difference sequence spaces. Soochow Journal of Mathematics 1995, 21(4):377–386.
Maddox IJ: On strong almost convergence. Mathematical Proceedings of the Cambridge Philosophical Society 1979, 85(2):345–350. 10.1017/S0305004100055766
Fast H: Sur la convergence statistique. Colloqium Mathematicum 1951, 2: 241–244.
Schoenberg IJ: The integrability of certain functions and related summability methods. The American Mathematical Monthly 1959, 66: 361–375. 10.2307/2308747
Šalát T: On statistically convergent sequences of real numbers. Mathematica Slovaca 1980, 30(2):139–150.
Fridy JA: On statistical convergence. Analysis 1985, 5(4):301–313.
Connor JS: The statistical and strong p -Cesàro convergence of sequences. Analysis 1988, 8(1–2):47–63.
Mursaleen M: λ -statistical convergence. Mathematica Slovaca 2000, 50(1):111–115.
Işik M: On statistical convergence of generalized difference sequences. Soochow Journal of Mathematics 2004, 30(2):197–205.
Malkowsky E, Savas E: Some λ -sequence spaces defined by a modulus. Archivum Mathematicum 2000, 36(3):219–228.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Işik, M. Generalized Vector-Valued Sequence Spaces Defined by Modulus Functions. J Inequal Appl 2010, 457892 (2010). https://doi.org/10.1155/2010/457892
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/457892
 and the other cases can be proved by using similar arguments. Let
and the other cases can be proved by using similar arguments. Let  and choose
and choose 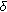 with
with  such that
such that 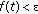 for
for 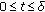 and for all
and for all  . Write
. Write 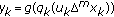 and consider
and consider 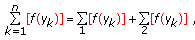
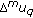 -Statistical Convergence
-Statistical Convergence