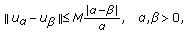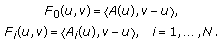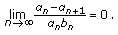- Research Article
- Open access
- Published:
Regularization Inertial Proximal Point Algorithm for Monotone Hemicontinuous Mapping and Inverse Strongly Monotone Mappings in Hilbert Spaces
Journal of Inequalities and Applications volume 2010, Article number: 451916 (2010)
Abstract
The purpose of this paper is to present a regularization variant of the inertial proximal point algorithm for finding a common element of the set of solutions for a variational inequality problem involving a hemicontinuous monotone mapping  and for a finite family of
and for a finite family of  -inverse strongly monotone mappings
-inverse strongly monotone mappings  from a closed convex subset
from a closed convex subset  of a Hilbert space
of a Hilbert space  into
into  .
.
1. Introduction
Let  be a real Hilbert space with inner product
be a real Hilbert space with inner product  and norm
and norm  . Let
. Let  be a closed convex subset of
be a closed convex subset of  . Denote the metric projection of
. Denote the metric projection of  onto
onto  by
by  , that is
, that is

for all 
Definition 1.1.
A set  is called monotone on
is called monotone on  if
if  has the following property:
has the following property:

A monotone mapping  in
in  is said to be maximal monotone if it is not properly contained in any other monotone mapping on
is said to be maximal monotone if it is not properly contained in any other monotone mapping on  . Equivalently, a monotone mapping
. Equivalently, a monotone mapping  is maximal monotone if
is maximal monotone if  for all
for all  , where
, where  denotes the range of
denotes the range of  .
.
Definition 1.2.
A mapping  is called hemicontinuous at a point
is called hemicontinuous at a point  in
in  if
if

Definition 1.3.
A mapping  of
of  into
into  is called
is called  -inverse strongly monotone if there exists a positive number
-inverse strongly monotone if there exists a positive number  such that
such that

for all  .
.
Definition 1.4.
A mapping  of
of  into
into  is called Lipschitz continuous on
is called Lipschitz continuous on  if there exists a positive number
if there exists a positive number  , named Lipschitz constant, such that
, named Lipschitz constant, such that

for all  .
.
It is easy to see that any  -inverse strongly monotone mapping
-inverse strongly monotone mapping  is monotone and Lipschitz continuous with Lipschitz constant
is monotone and Lipschitz continuous with Lipschitz constant  . When
. When  ,
,  is said to be nonexpansive mapping. Note that a nonexpansive mapping in Hilbert space is
is said to be nonexpansive mapping. Note that a nonexpansive mapping in Hilbert space is  -inverse strongly monotone [1].
-inverse strongly monotone [1].
Definition 1.5.
A mapping  is said to be strictly pseudocontractive, if there exists a constant
is said to be strictly pseudocontractive, if there exists a constant  such that
such that

Clearly, when  ,
,  is nonexpansive. Therefore, the class of
is nonexpansive. Therefore, the class of  -strictly pseudocontractive mappings includes the class of nonexpansive mappings.
-strictly pseudocontractive mappings includes the class of nonexpansive mappings.
Definition 1.6.
A mapping  from
from  into
into  is said to be demiclosed at a point
is said to be demiclosed at a point  if whenever
if whenever  is a sequence in
is a sequence in  such that
such that  and
and  , then
, then  where the symbols
where the symbols  and
and  denote the strong and weak convergences of any sequence, respectively.
denote the strong and weak convergences of any sequence, respectively.
The variational inequality problem is to find  such that
such that

for all  . The set of solutions of the variational inequality problem (1.7) is denoted by
. The set of solutions of the variational inequality problem (1.7) is denoted by  .
.
Let  be a finite family of
be a finite family of  -inverse strongly monotone mappings from
-inverse strongly monotone mappings from  into
into  with the set of solutions denoted by
with the set of solutions denoted by  And set
And set

The problem which will be studied in this paper is to find an element

with assumption  .
.
A following example shows the fact that  Consider the following case:
Consider the following case:


,  where
where  denote the metric projections of
denote the metric projections of  onto
onto  , and the matrix
, and the matrix  has the elements
has the elements  ,
,  , and
, and  . Then,
. Then,  is
is  -inverse strongly monotone. Clearly,
-inverse strongly monotone. Clearly,  if and only if
if and only if  . It means that
. It means that  . Consequently,
. Consequently,  . It is easy to see that
. It is easy to see that  is monotone, and for
is monotone, and for  ,
,  if and only if
if and only if  . Therefore,
. Therefore,  .
.
Since for a nonexpansive mapping  , the mapping
, the mapping  is
is  -inverse strongly monotone, the problem of finding an element of
-inverse strongly monotone, the problem of finding an element of  , where
, where  denotes the set of fixed points of the nonexpansive mapping
denotes the set of fixed points of the nonexpansive mapping  , is equivalent to that of finding an element of
, is equivalent to that of finding an element of  , where
, where  denotes the set of solutions of the mapping
denotes the set of solutions of the mapping  , and contained in the class of problem (1.9).
, and contained in the class of problem (1.9).
The case, when  is
is  -inverse strongly monotone and
-inverse strongly monotone and  , where
, where  is nonexpansive, is studied in [2].
is nonexpansive, is studied in [2].
Theorem 1.7 (see [2]).
Let  be a nonempty closed convex subset of a Hilbert space
be a nonempty closed convex subset of a Hilbert space  . Let
. Let  be a
be a  -inverse strongly monotone mapping of
-inverse strongly monotone mapping of  into
into  for
for  , and let
, and let  be a nonexpansive mapping of
be a nonexpansive mapping of  into itself such that
into itself such that  . Let
. Let  be a sequence generated by
be a sequence generated by

where  for some
for some  and
and  for some
for some  . Then
. Then  converges weakly to
converges weakly to  , where
, where

For finding an element of the set  , one can use the extragradient method proposed in [3] for the case of finite-dimensional spaces. In the infinite-dimensional Hilbert spaces, the weak convergence result of the extragradient method was proved [1] and it was improved to the strong convergence in [4].
, one can use the extragradient method proposed in [3] for the case of finite-dimensional spaces. In the infinite-dimensional Hilbert spaces, the weak convergence result of the extragradient method was proved [1] and it was improved to the strong convergence in [4].
On the other hand, when  , (1.7) is equivalent to the operator equation
, (1.7) is equivalent to the operator equation

involving a maximal monotone  , since the domain of
, since the domain of  is the whole space
is the whole space  , and
, and  is hemicontinuous ([5, 6]). A zero element of (1.13) can be approximated by the inertial proximal point algorithm
is hemicontinuous ([5, 6]). A zero element of (1.13) can be approximated by the inertial proximal point algorithm

where  and
and  are two sequences of positive numbers.
are two sequences of positive numbers.
Note that the inertial proximal algorithm was proposed by Alvarez [7] in the context of convex minimization. Afterwards, Alvarez and Attouch [8] considered its extension to maximal monotone operators. Recently, Moudafi [9] applied this algorithm for variational inequalities; Moudafi and Elisabeth [10] studied the algorithm by using enlargement of a maximal monotone operator; Moudafi and Oliny [11] considered convergence of a splitting inertial proximal method. The main results in these papers are the weak convergence of the algorithm in Hilbert spaces.
In this paper, by introducing a regularization process we shall show that by adding the regularization term to the inertial proximal point algorithm, called regularization inertial proximal point algorithm, we obtain the strong convergence of the algorithm, and the strong convergence is proved for the general case  are
are  -inverse strongly monotone nonself mappings of
-inverse strongly monotone nonself mappings of  into
into  ;
;  may not be
may not be 
 is monotone and hemicontinuous at each point
is monotone and hemicontinuous at each point  .
.
2. Main Results
Let  be an equilibrium bifunction from
be an equilibrium bifunction from  to
to  , that is
, that is  for every
for every  In addition, assume that
In addition, assume that  is convex and lower semicontinuous in the variable
is convex and lower semicontinuous in the variable  for each fixed
for each fixed  .
.
The equilibrium problem for  is to find
is to find  such that
such that

First, we recall several well-known facts in [12, 13] which are necessary in the proof of our results.
The equilibrium bifunction  is said to be
is said to be
(i)monotone, if for all  , we have
, we have

(ii)strongly monotone with constant  , if, for all
, if, for all  , we have
, we have

(iii)hemicontinuous in the variable  for each fixed
for each fixed  , if
, if

We can get the following proposition from the above definitions.
Proposition 2.1.
-
(i)
If
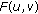 is hemicontinuous in the first variable for each fixed
is hemicontinuous in the first variable for each fixed 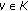 and
and 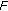 is monotone, then
is monotone, then 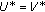 , where
, where 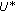 is the solution set of (2.1),
is the solution set of (2.1), 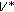 is the solution set of
is the solution set of 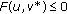 for all
for all 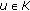 , and they are closed and convex.
, and they are closed and convex. -
(ii)
If
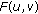 is hemicontinuous in the first variable for each
is hemicontinuous in the first variable for each 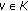 and
and  is strongly monotone, then
is strongly monotone, then 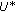 is a nonempty singleton.
is a nonempty singleton.
Lemma 2.2 (see [14]).
Let  be the sequences of positive numbers satisfying the conditions:
be the sequences of positive numbers satisfying the conditions:
(i) ,
,
(ii) ,
, 
Then, 
Lemma 2.3 (see [15]).
Let  be a nonempty closed convex subset of a Hilbert space
be a nonempty closed convex subset of a Hilbert space  and
and  a strictly pseudocontractive mapping. Then
a strictly pseudocontractive mapping. Then  is demiclosed at zero.
is demiclosed at zero.
We construct a regularization solution  for (1.9) by solving the following variational inequality problem: find
for (1.9) by solving the following variational inequality problem: find  such that
such that

where  , is the regularization parameter.
, is the regularization parameter.
We have the following result.
Theorem 2.4.
Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . Let
. Let  be a
be a  -inverse strongly monotone mapping of
-inverse strongly monotone mapping of  into
into  , and let
, and let  be a monotone hemicontinuous mapping of
be a monotone hemicontinuous mapping of  into
into  such that
such that  . Then, we have
. Then, we have
(i)For each  , the problem (2.5) has a unique solution
, the problem (2.5) has a unique solution  ;
;
(ii)If  then
then  and
and  for all
for all 
-
(iii)
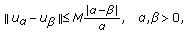 (2.6)
(2.6)
where  is a positive constant.
is a positive constant.
Proof.
-
(i)
Let
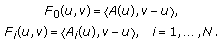 (2.7)
(2.7)
Then, problem (2.5) has the following form: find  such that
such that

where

It is not difficult to verify that  are the monotone bifunctions, and for each fixed
are the monotone bifunctions, and for each fixed  , they are hemicontinuous in the variable
, they are hemicontinuous in the variable  . Therefore,
. Therefore,  also is monotone hemicontinuous in the variable
also is monotone hemicontinuous in the variable  for each fixed
for each fixed  . Moreover, it is strongly monotone with constant
. Moreover, it is strongly monotone with constant  . Hence, (2.8) (consequently (2.5)) has a unique solution
. Hence, (2.8) (consequently (2.5)) has a unique solution  for each
for each  .
.
-
(ii)
Now we prove that

Since 
 and
and 
 ,
,  and
and

By adding the last inequality to (2.8) in which  is replaced by
is replaced by  and using the properties of
and using the properties of  , we obtain
, we obtain

that implies (2.10). It means that  is bounded. Let
is bounded. Let  , as
, as  . Since
. Since  is closed and convex,
is closed and convex,  is weakly closed. Hence
is weakly closed. Hence  . We prove that
. We prove that  . From the monotone property of
. From the monotone property of  and (2.8), it follows
and (2.8), it follows

Letting  , we obtain
, we obtain  for any
for any  By virtue of Proposition 2.1, we have
By virtue of Proposition 2.1, we have 
Now we show that  for all
for all  From (2.8),
From (2.8),  for any
for any  , and the monotone property of
, and the monotone property of  , it implies that
, it implies that

On the base of  -inverse strongly monotone property of
-inverse strongly monotone property of  , the monotone property of
, the monotone property of  ,
,  ,
,  , for all
, for all  ,
,  . From the last inequality, we have
. From the last inequality, we have

Tending  in the last inequality, we obtain
in the last inequality, we obtain

Since  is
is  -inverse strongly monotone, the mapping
-inverse strongly monotone, the mapping  satisfies (1.6), where
satisfies (1.6), where  Because
Because  , we have
, we have  . When
. When  , this inequality will not be changed if
, this inequality will not be changed if  is replaced by
is replaced by  . Thus,
. Thus,  is strictly pseudocontractive. Applying Lemma 2.2, we can conclude that
is strictly pseudocontractive. Applying Lemma 2.2, we can conclude that  It means that
It means that  It is well known that the sets
It is well known that the sets  are closed and convex. Therefore,
are closed and convex. Therefore,  is also closed and convex. Then, from (2.10) it implies that
is also closed and convex. Then, from (2.10) it implies that  is the unique element in
is the unique element in  having a minimal norm. Consequently, we have
having a minimal norm. Consequently, we have

(iii) From (2.8) and the properties of  , for each
, for each  , it follows
, it follows

or

For each 
 is bounded since the operator
is bounded since the operator  is Lipschitzian with Lipschitz constants
is Lipschitzian with Lipschitz constants  . Using (2.10), the boundedness of
. Using (2.10), the boundedness of  and the Lagrange's mean-value theorem for the function
and the Lagrange's mean-value theorem for the function  ,
,  ,
,  , on
, on  if
if  or
or  if
if  , we have conclusion (iii). This completes the proof.
, we have conclusion (iii). This completes the proof.
Remark 2.5.
Obviously, if  , where
, where  is the solution of (2.8) with
is the solution of (2.8) with  , as
, as  , then
, then 
Now, we consider the regularization inertial proximal point algorithm

Clearly,

is a bifunction. Moreover, it is strongly monotone with  By Proposition 2.1, there exists a unique element
By Proposition 2.1, there exists a unique element  satisfying (2.20).
satisfying (2.20).
Theorem 2.6.
Let  be a nonempty closed convex subset of a Hilbert space
be a nonempty closed convex subset of a Hilbert space  . Let
. Let  be a
be a  -inverse strongly monotone mapping of
-inverse strongly monotone mapping of  into
into  , and let
, and let  be a monotone hemicontinuous mapping of
be a monotone hemicontinuous mapping of  into
into  such that
such that  . Assume that the parameters
. Assume that the parameters  , and
, and  are chosen such that
are chosen such that
(i) ,
, ,
,
(ii) ,
,
(iii)
-
(iv)
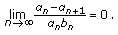 (2.22)
(2.22)
Then the sequence  defined by (2.20) converges strongly to the element
defined by (2.20) converges strongly to the element  as
as  .
.
Proof.
From (2.20) it follows

By the similar argument, from (2.5) it implies

where  is the solution of (2.5) when
is the solution of (2.5) when  is replaced by
is replaced by  . By setting
. By setting  in (2.23) and
in (2.23) and  in (2.24) and adding one obtained result to the other, we have,
in (2.24) and adding one obtained result to the other, we have,

Therefore, from the monotone property of the mappings  ,
,  , it follows
, it follows

From (2.23), (2.5) with  and
and  , we have
, we have

where

Since the seris in (iii) is convergent,  Consequently,
Consequently,  From Lemma 2.2, it follows that
From Lemma 2.2, it follows that  as
as  .
.
On the other hand,  as
as  . Therefore, we have
. Therefore, we have  as
as  This completes the proof.
This completes the proof.
Remark 2.7.
The sequences  and
and  which are defined by
which are defined by

with  satisfy all conditions in Theorem 2.6.
satisfy all conditions in Theorem 2.6.
References
Nadezhkina N, Takahashi W: Weak convergence theorem by an extragradient method for nonexpansive mappings and monotone mappings. Journal of Optimization Theory and Applications 2006, 128(1):191–201. 10.1007/s10957-005-7564-z
Takahashi W, Toyoda M: Weak convergence theorems for nonexpansive mappings and monotone mappings. Journal of Optimization Theory and Applications 2003, 118(2):417–428. 10.1023/A:1025407607560
Korpelevič GM: An extragradient method for finding saddle points and for other problems. Èkonomika i Matematicheskie Metody 1976, 12(4):747–756.
Zeng L-C, Yao J-C: Strong convergence theorem by an extragradient method for fixed point problems and variational inequality problems. Taiwanese Journal of Mathematics 2006, 10(5):1293–1303.
Barbu V: Nonlinear Semigroups and Differential Equations in Banach Spaces. Editura Academiei Republicii Socialiste România, Bucharest, Romania; 1976:352.
Brezis H: Opératuer maximaux monotones. In Mathematics Studies. Volume 5. North-Holland, Amsterdam, The Netherlands; 1973.
Alvarez F: On the minimizing property of a second order dissipative system in Hilbert spaces. SIAM Journal on Control and Optimization 2000, 38(4):1102–1119. 10.1137/S0363012998335802
Alvarez F, Attouch H: An inertial proximal method for maximal monotone operators via discretization of a nonlinear oscillator with damping. Set-Valued Analysis 2001, 9(1–2):3–11.
Moudafi A: A hybrid inertial projection-proximal method for variational inequalities. Journal of Inequalities in Pure and Applied Mathematics 2004., 5(3, article 63):
Moudafi A, Elisabeth E: An approximate inertial proximal method using the enlargement of a maximal monotone operator. International Journal of Pure and Applied Mathematics 2003, 5(3):283–299.
Moudafi A, Oliny M: Convergence of a splitting inertial proximal method for monotone operators. Journal of Computational and Applied Mathematics 2003, 155(2):447–454.
Blum E, Oettli W: From optimization and variational inequalities to equilibrium problems. Mathematics Students 1994, 63: 123–145.
Oettli W: A remark on vector-valued equilibria and generalized monotonicity. Acta Mathematica Vietnamica 1997, 22(1):213–221.
Vasin VV, Ageev AL: Incorrect Problems with Priori Information. Nauka, Ekaterinburg, Russia; 1993:263.
Osilike MO, Udomene A: Demiclosedness principle and convergence theorems for strictly pseudocontractive mappings of Browder-Petryshyn type. Journal of Mathematical Analysis and Applications 2001, 256(2):431–445. 10.1006/jmaa.2000.7257
Acknowledgment
This work was supported by the Kyungnam University Research Fund 2009.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kim, J., Buong, N. Regularization Inertial Proximal Point Algorithm for Monotone Hemicontinuous Mapping and Inverse Strongly Monotone Mappings in Hilbert Spaces. J Inequal Appl 2010, 451916 (2010). https://doi.org/10.1155/2010/451916
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/451916
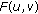 is hemicontinuous in the first variable for each fixed
is hemicontinuous in the first variable for each fixed 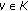 and
and 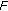 is monotone, then
is monotone, then 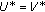 , where
, where 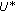 is the solution set of (2.1),
is the solution set of (2.1), 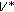 is the solution set of
is the solution set of 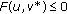 for all
for all 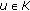 , and they are closed and convex.
, and they are closed and convex.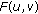 is hemicontinuous in the first variable for each
is hemicontinuous in the first variable for each 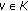 and
and  is strongly monotone, then
is strongly monotone, then 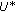 is a nonempty singleton.
is a nonempty singleton.