- Research Article
- Open access
- Published:
Estimates of 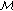 -Harmonic Conjugate Operator
-Harmonic Conjugate Operator
Journal of Inequalities and Applications volume 2010, Article number: 435450 (2010)
Abstract
We define the  -harmonic conjugate operator
-harmonic conjugate operator  and prove that for
and prove that for  , there is a constant
, there is a constant  such that
such that  for all
for all  if and only if the nonnegative weight
if and only if the nonnegative weight  satisfies the
satisfies the  -condition. Also, we prove that if there is a constant
-condition. Also, we prove that if there is a constant  such that
such that  for all
for all  , then the pair of weights
, then the pair of weights  satisfies the
satisfies the  -condition.
-condition.
1. Introduction
Let  be the unit ball of
be the unit ball of  with norm
with norm  where
where  is the Hermitian inner product, let
is the Hermitian inner product, let  be the unit sphere, and,
be the unit sphere, and,  be the rotation-invariant probability measure on
be the rotation-invariant probability measure on  .
.
In [1], for  , we defined the kernel
, we defined the kernel  by
by

where  is the Cauchy kernel and
is the Cauchy kernel and  is the invariant Poisson kernel. Thus for each
is the invariant Poisson kernel. Thus for each  , the kernel
, the kernel  is
is  -harmonic. And for all
-harmonic. And for all  , the ball algebra, such that
, the ball algebra, such that  is real, the reproducing property of
is real, the reproducing property of  (
( of [2]) gives
of [2]) gives

For that reason,  is called the
is called the  -harmonic conjugate kernel.
-harmonic conjugate kernel.
For  ,
,  , the
, the  -harmonic conjugate function of
-harmonic conjugate function of  , on
, on  is defined by
is defined by

since the limit exists almost everywhere. For  , the definition of
, the definition of  is the same as the classical harmonic conjugate function [3, 4]. Many properties of
is the same as the classical harmonic conjugate function [3, 4]. Many properties of  -harmonic conjugate function come from those of Cauchy integral and invariant Poisson integral. Indeed the following properties of
-harmonic conjugate function come from those of Cauchy integral and invariant Poisson integral. Indeed the following properties of  follow directly from Chapters 5 and 6 of [2].
follow directly from Chapters 5 and 6 of [2].
()As an operator,  is of weak type (1.5) and bounded on
is of weak type (1.5) and bounded on  for
for  .
.
()If  , then
, then  for all
for all  and if
and if  , then
, then  .
.
()If  is in the Euclidean Lipschitz space of order
is in the Euclidean Lipschitz space of order  for
for  , then so is
, then so is  .
.
Also, in [1], it is shown that  is bounded on the Euclidean Lipschitz space of order
is bounded on the Euclidean Lipschitz space of order  for
for  , and bounded on
, and bounded on  .
.
In this paper, we focus on the weighted norm inequality for  -harmonic conjugate functions. In the past, there have been many results on weighted norm inequalities and related subjects, for which the two books [3, 4] provide good references. Some classical results include those of M. Riesz in 1924 about the
-harmonic conjugate functions. In the past, there have been many results on weighted norm inequalities and related subjects, for which the two books [3, 4] provide good references. Some classical results include those of M. Riesz in 1924 about the  boundedness of harmonic conjugate functions on the unit circle for
boundedness of harmonic conjugate functions on the unit circle for  [3, Theorem
[3, Theorem  of Chapter 3] and [3, Theorems
of Chapter 3] and [3, Theorems  and
and  of Chapter 6] about the close relation between
of Chapter 6] about the close relation between  -condition of the weight and the
-condition of the weight and the  boundedness of the Hardy-Littlewood maximal operator and Hilbert transform on
boundedness of the Hardy-Littlewood maximal operator and Hilbert transform on  . In 1973, Hunt et al. [5] proved that, for
. In 1973, Hunt et al. [5] proved that, for  , conjugate functions are bounded on weighted measured Lebesgue space if and only if the weight satisfies
, conjugate functions are bounded on weighted measured Lebesgue space if and only if the weight satisfies  -condition. It should be noted that in 1986 the boundedness of the Cauchy transform on the Siegel upper half-plane in
-condition. It should be noted that in 1986 the boundedness of the Cauchy transform on the Siegel upper half-plane in  was proved by Dorronsoro [6]. Here in this paper, we provide an analogue of that of [5] and [3, Theorems
was proved by Dorronsoro [6]. Here in this paper, we provide an analogue of that of [5] and [3, Theorems  and
and  of Chapter 6].
of Chapter 6].
To define the  -condition on
-condition on  , we let
, we let  be a nonnegative integrable function on
be a nonnegative integrable function on  . For
. For  , we say that
, we say that  satisfies the
satisfies the  -condition if
-condition if

where  is a nonisotropic ball of
is a nonisotropic ball of  .
.
Here is the first and the main theorem.
Theorem 1.1.
Let  be a nonnegative integrable function on
be a nonnegative integrable function on  . Then for
. Then for  , there is a constant
, there is a constant  such that
such that

if and only if  satisfies the
satisfies the  -condition.
-condition.
In succession of classical weighted norm inequalities, starting from Muckenhoupt's result in 1975 [7], there have been extensive studies on two-weighted norm inequalities. Here, we define the  -condition for two weights. For a pair
-condition for two weights. For a pair  of two nonnegative integrable functions, we say that
of two nonnegative integrable functions, we say that  satisfies the
satisfies the  -condition if
-condition if

where  is a nonisotropic ball of
is a nonisotropic ball of  . As mentioned above, in [7], Muckenhoupt derives a necessary and sufficient condition on two-weighted norm inequalities for the Poisson integral operator, and then in [8], Muckenhoupt and Wheeden provided two-weighted norm inequalities for the Hardy-Littlewood maximal operator and the Hilbert transform. We admit that there are, henceforth, numerous splendid results on two-weighted norm inequalities but left unmentioned here.
. As mentioned above, in [7], Muckenhoupt derives a necessary and sufficient condition on two-weighted norm inequalities for the Poisson integral operator, and then in [8], Muckenhoupt and Wheeden provided two-weighted norm inequalities for the Hardy-Littlewood maximal operator and the Hilbert transform. We admit that there are, henceforth, numerous splendid results on two-weighted norm inequalities but left unmentioned here.
In this paper we provide a two-weighted norm inequality for  -harmonic conjugate operator as our next theorem, by the method somewhat similar to the proof of the main theorem. For a pair
-harmonic conjugate operator as our next theorem, by the method somewhat similar to the proof of the main theorem. For a pair  , the generalization of the necessity in Theorem (1.5) is as follows.
, the generalization of the necessity in Theorem (1.5) is as follows.
Theorem 1.2.
Let  be a pair of nonnegative integrable functions on
be a pair of nonnegative integrable functions on  . If for
. If for  , there is a constant
, there is a constant  such that
such that

then the pair  satisfies the
satisfies the  -condition.
-condition.
The proofs of Theorems 1.1 and 1.2 will be given in Section 2. We start Section 2 by introducing the sharp maximal function and a lemma on the sharp maximal function, which plays an important role in the proof of the main theorem. In the final section, as an appendix, we introduce John-Nirenberg's inequality on  and then, as an application, we attach some properties of
and then, as an application, we attach some properties of  weights on
weights on  in relation with
in relation with  , which are similar to those on the Euclidean space.
, which are similar to those on the Euclidean space.
2. Proofs
Definition 2.1.
For  and
and  , the sharp maximal function
, the sharp maximal function  on
on  is defined by
is defined by

where the supremum is taken over all the nonisotropic balls  containing
containing  and
and  stands for the average of
stands for the average of  over
over  .
.
The sharp maximal operator  is an analogue of the Hardy-Littlewood maximal operator
is an analogue of the Hardy-Littlewood maximal operator  , which satisfies
, which satisfies  . The proof of the following lemma is essentially the same as that of the Theorem
. The proof of the following lemma is essentially the same as that of the Theorem  of [4]; so we omit its proof.
of [4]; so we omit its proof.
Lemma 2.2.
Let  and
and  satisfy
satisfy  -condition. Then there is a constant
-condition. Then there is a constant  such that
such that

for all  .
.
Now we will prove Theorem 1.1.
Proof of Theorem 1.1.
First, we prove that (1.5) implies that  satisfies the
satisfies the  -condition.
-condition.
If  , then by a direct calculation we get
, then by a direct calculation we get

If  and
and  , then we get
, then we get  . Thus if
. Thus if  , then for
, then for  , we have
, we have  . Hence there exist positive constants
. Hence there exist positive constants  and
and  such that
such that

for any nonnegative function  , where
, where  depends only on the distance between
depends only on the distance between  and
and  . Suppose that
. Suppose that  and
and  are nonintersecting with positive distance nonisotropic balls with radius sufficiently small
are nonintersecting with positive distance nonisotropic balls with radius sufficiently small  , and that they are contained in another small nonisotropic ball, for example, with radius
, and that they are contained in another small nonisotropic ball, for example, with radius  . Choose a nonnegative function
. Choose a nonnegative function  supported in
supported in  . Then from (2.4), for almost all
. Then from (2.4), for almost all  we have
we have

Since  , there is a constant
, there is a constant  such that
such that  . Thus for almost all
. Thus for almost all  , we get
, we get

Putting  and integrating (2.6) over
and integrating (2.6) over  after being multiplied by
after being multiplied by  , we get
, we get

However by (1.5) there exists a number  such that
such that

Thus we get

Similarly, putting  and integrating (2.6) over
and integrating (2.6) over  after being multiplied by
after being multiplied by  and then using (1.5), we also have
and then using (1.5), we also have

Therefore, the integrals of  over
over  and
and  are equivalent.
are equivalent.
Now for a given constant  , put
, put  in (2.6) and integrate over
in (2.6) and integrate over  . We have
. We have

Thus we get

Finally take  and apply (2.10) to (2.12), then we have the inequality
and apply (2.10) to (2.12), then we have the inequality

for every ball  with radius less than or equal to
with radius less than or equal to  at any point of
at any point of  . (Here, note that the right hand side of the above is independent of
. (Here, note that the right hand side of the above is independent of  and particularly
and particularly  because
because  depends only on the distance between
depends only on the distance between  and
and  .) Therefore,
.) Therefore,

where the constant  is independent of
is independent of  . Consequently, we have the desired
. Consequently, we have the desired  -condition. And this proves the necessity of the
-condition. And this proves the necessity of the  -condition for (1.5).
-condition for (1.5).
Conversely, we suppose that  and
and  satisfies the
satisfies the  -condition and then we will prove that (1.5) holds. To do this we will first prove the following. Claim (i). Let
-condition and then we will prove that (1.5) holds. To do this we will first prove the following. Claim (i). Let . Then for
. Then for , there is a constant
, there is a constant such that
such that for almost all
for almost all .
.
To prove Claim (i), for a fixed  , it suffices to show that for each
, it suffices to show that for each  there are constants
there are constants  and
and  depending only on
depending only on  such that
such that

Now, we write

Since  , we have
, we have 
Define

Then  is continuous on
is continuous on  . By setting
. By setting  in (2.15), we shall prove the Claim. The integral in (2.15) is estimated as
in (2.15), we shall prove the Claim. The integral in (2.15) is estimated as

Estimate of  . By Hölder's inequality we get
. By Hölder's inequality we get

since  is bounded on
is bounded on  . (Here, throughout the proof for notational simplicity, the letter
. (Here, throughout the proof for notational simplicity, the letter  alone will denote a positive constant, independent of
alone will denote a positive constant, independent of  , whose value may change from line to line.) Now by replacing
, whose value may change from line to line.) Now by replacing  by
by  , we get
, we get

Thus by applying Hölder's inequality in the last term of the above, we see that there is a constant  such that
such that

Now we estimate  . Since
. Since  on
on  , we have
, we have

By Lemma  of [2], we get an upper bound such that
of [2], we get an upper bound such that

where  is an absolute constant.
is an absolute constant.
Write  Then the integral of (2.23) is equal to
Then the integral of (2.23) is equal to

Thus there exist  and
and  such that
such that

as we complete the proof of the claim.
Next, we fix  and let
and let  . Then by Lemma maximal inequality there is a constant
. Then by Lemma maximal inequality there is a constant  such that
such that

Take  such that
such that  . By the above Claim (i), the last term of the above inequalities is bounded by some constant (depending on
. By the above Claim (i), the last term of the above inequalities is bounded by some constant (depending on  and
and  ) times
) times

where two constants  and
and  depend on
depend on  and
and  , which proves (1.5) and this completes the proof of Theorem 1.1.
, which proves (1.5) and this completes the proof of Theorem 1.1.
Now, we will prove Theorem 1.2 by taking slightly a roundabout way from the proof of Theorem 1.1.
Proof of Theorem 1.2.
Assume the inequality (1.7). Let  and
and  be nonintersecting nonisotropic balls with positive distance, and with radius sufficiently small
be nonintersecting nonisotropic balls with positive distance, and with radius sufficiently small  .
.
Let  be supported in
be supported in  . Then from (2.4), there is a positive constant
. Then from (2.4), there is a positive constant  such that for all
such that for all  ,
,

where  depends only on the distance between
depends only on the distance between  and
and  . Also from the fact that
. Also from the fact that  , for some constant
, for some constant  depending only on
depending only on  , the integral of (2.28) has the lower bound such as
, the integral of (2.28) has the lower bound such as

Thus for almost all  , we get
, we get

Putting  and integrating (2.30) over
and integrating (2.30) over  after being multiplied by
after being multiplied by  , we get
, we get

However, by (1.7) there exists a number  such that
such that

Thus,

For a constant  which will be chosen later, put
which will be chosen later, put  in (2.30), multiply
in (2.30), multiply  on both sides, and integrate over
on both sides, and integrate over  . We have
. We have

By (1.7), we arrive at

Taking  in (2.35), we have the inequality
in (2.35), we have the inequality

for all balls  ,
,  with radius less than or equal to
with radius less than or equal to  and the distance between two balls greater then
and the distance between two balls greater then  at any point of
at any point of  .
.
Here, unlike the proof of Theorem 1.1, we can not derive the equivalence between  and
and  in a straightforward method, for
in a straightforward method, for 
 . For this reason, it is not allowed to replace
. For this reason, it is not allowed to replace  by
by  directly in (2.36). However, such difficulty can be overcome using the following method. By the symmetric process of the proof, we can interchange
directly in (2.36). However, such difficulty can be overcome using the following method. By the symmetric process of the proof, we can interchange  with
with  in (2.36). Thus, for all such balls,
in (2.36). Thus, for all such balls,

Now multiply two equations (2.36) and (2.37) by side. Since  , we have
, we have

Let us note that  depends on the distance between
depends on the distance between  and
and  . Taking supremum over all
. Taking supremum over all  -balls, we get
-balls, we get

and the proof of Theorem 1.2 is complete.
References
Lee J, Rim KS: Properties of the -harmonic conjugate operator. Canadian Mathematical Bulletin 2003, 46(1):113–121. 10.4153/CMB-2003-011-x
Rudin W: Function Theory in the Unit Ball of ℂn. Springer, New York, NY, USA; 1980.
Garnett JB: Bounded Analytic Functions, Pure and Applied Mathematics. Volume 96. Academic Press, New York, NY, USA; 1981:xvi+467.
García-Cuerva J, Rubio de Francia JL: Weighted Norm Inequalities and Related Topics, North-Holland Mathematics Studies. Volume 116. North-Holland, Amsterdam, The Netherlands; 1985:x+604.
Hunt R, Muckenhoupt B, Wheeden R: Weighted norm inequalities for the conjugate function and Hilbert transform. Transactions of the American Mathematical Society 1973, 176: 227–251.
Dorronsoro JR: Weighted Hardy spaces on Siegel's half planes. Mathematische Nachrichten 1986, 125: 103–119.
Muckenhoupt B: Two weight function norm inequalities for the Poisson integral. Transactions of the American Mathematical Society 1975, 210: 225–231.
Muckenhoupt B, Wheeden RL: Two weight function norm inequalities for the Hardy-Littlewood maximal function and the Hilbert transform. Studia Mathematica 1976, 55(3):279–294.
Acknowledgments
The authors want to express their heartfelt gratitude to the anonymous referee and the editor for their important comments which are significantly helpful for the authors' further research. The authors were partially supported by Grant no. 200811014.01 and no. 200911051, Sogang University.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
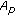 -Condition and BMO
-Condition and BMO
Let  be a nonisotropic ball of
be a nonisotropic ball of  . The space
. The space  consists of all
consists of all  satisfying
satisfying

where  is the average of
is the average of  over
over  .
.  becomes a Banach space provided that we identify functions which differ by a constant. Since both definitions of
becomes a Banach space provided that we identify functions which differ by a constant. Since both definitions of  -condition and
-condition and  are concerned about the local average of a function, it is natural for us to mention the relation between these concepts. In this section, we show that an
are concerned about the local average of a function, it is natural for us to mention the relation between these concepts. In this section, we show that an  weight on
weight on  is indeed closely related to the
is indeed closely related to the  . Proposition A.4 and Lemma A.3 tell about it. The proof of Proposition A.4 comes from John-Nirenberg's inequality (Lemma A.3) which states as follows.
. Proposition A.4 and Lemma A.3 tell about it. The proof of Proposition A.4 comes from John-Nirenberg's inequality (Lemma A.3) which states as follows.
Lemma A.3 (John-Nirenberg's inequality).
Let  and
and  be not intersecting the north pole. Then there exist positive constants
be not intersecting the north pole. Then there exist positive constants  and
and  , independent of
, independent of  and
and  , such that
, such that

for every  .
.
The proof of Lemma A.3 is parallel to the proof of the classical John-Nirenberg's inequality on  [3, Theorem
[3, Theorem  of Chapter 6]. However, it is somewhat more complicated, and moreover, the details of the proof run off our aim of the paper. So we decide to omit the proof of Lemma A.3.
of Chapter 6]. However, it is somewhat more complicated, and moreover, the details of the proof run off our aim of the paper. So we decide to omit the proof of Lemma A.3.
The next proposition is about the  weight and
weight and  on
on  . Likewise, on the Euclidean space, by Jensen's inequality and the classical John-Nirenberg's inequality, we can see that the Euclidean analogue of Proposition A.4 is also true.
. Likewise, on the Euclidean space, by Jensen's inequality and the classical John-Nirenberg's inequality, we can see that the Euclidean analogue of Proposition A.4 is also true.
Proposition A.4.
Let  be a nonnegative integrable function on
be a nonnegative integrable function on  . Then
. Then  if and only if
if and only if  satisfies the
satisfies the  -condition for some
-condition for some  .
.
Proof.
We prove the necessity first. Suppose  . Let
. Let  denote a nonisotropic ball, and
denote a nonisotropic ball, and  . Now consider integral
. Now consider integral

which is less than or equal to

By change of variables, the integral term of the above is equal to

John-Nirenberg's inequality implies that there exist positive constants  and
and  , independent of
, independent of  , such that
, such that

Now we take  , and then we define
, and then we define

By the above choice of  and
and  , for each nonisotropic ball
, for each nonisotropic ball  , we have the inequality
, we have the inequality

Therefore we have

which means that  satisfies the
satisfies the  -condition.
-condition.
Conversely, suppose that there is  such that
such that  satisfies the
satisfies the  -condition. Then by Jensen's inequality it suffices to show that
-condition. Then by Jensen's inequality it suffices to show that

Let us note that

Since both integrals  and
and  are bounded in essentially the same way, we only do
are bounded in essentially the same way, we only do  . From Jensen's inequality once more, we have
. From Jensen's inequality once more, we have

Since  satisfies the
satisfies the  -condition, we finish the sufficiency and this completes the proof of the proposition.
-condition, we finish the sufficiency and this completes the proof of the proposition.
Let  satisfy the
satisfy the  -condition and
-condition and  . Then, since
. Then, since  , Hölder's inequality implies that
, Hölder's inequality implies that

This means that  satisfies the
satisfies the  -condition. Also we can easily see that
-condition. Also we can easily see that  satisfies the
satisfies the  -condition for
-condition for  . From this and Proposition A.4, we get the following corollary.
. From this and Proposition A.4, we get the following corollary.
Corollary A.5.
Let  and let
and let  be a nonnegative integrable function on
be a nonnegative integrable function on  such that
such that  satisfies the
satisfies the  -condition for some
-condition for some  . Then
. Then  .
.
Proof.
If  , then
, then  satisfies the
satisfies the  -condition. Thus Proposition A.4 implies
-condition. Thus Proposition A.4 implies  . If
. If  , then
, then  satisfies the
satisfies the  -condition for
-condition for  , which implies that
, which implies that  satisfies the
satisfies the  -condition. Thus by Proposition A.4, we get
-condition. Thus by Proposition A.4, we get  consequently
consequently  .
.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Lee, J., Rim, K. Estimates of 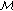 -Harmonic Conjugate Operator.
J Inequal Appl 2010, 435450 (2010). https://doi.org/10.1155/2010/435450
-Harmonic Conjugate Operator.
J Inequal Appl 2010, 435450 (2010). https://doi.org/10.1155/2010/435450
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/435450
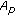 -Condition and BMO
-Condition and BMO