- Research Article
- Open access
- Published:
Characterization of 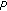 -Core and Absolute Equivalence of Double Sequences
-Core and Absolute Equivalence of Double Sequences
Journal of Inequalities and Applications volume 2010, Article number: 432059 (2010)
Abstract
The  -core of a double sequence has been defined and it is studied by many authors. In this paper, we have determined two permutations
-core of a double sequence has been defined and it is studied by many authors. In this paper, we have determined two permutations  and
and  on the set of natural numbers for which
on the set of natural numbers for which  for all
for all  .
.
1. Introduction and Preliminaries
A double sequence  is said to be convergent in the Pringsheim sense or P-convergent if for every
is said to be convergent in the Pringsheim sense or P-convergent if for every  there exists
there exists  such that
such that  whenever
whenever  [1]. In this case, we write
[1]. In this case, we write  . By
. By  , we mean the space of all P-convergent sequences.
, we mean the space of all P-convergent sequences.
A double sequence  is said to be bounded if there exists a positive number
is said to be bounded if there exists a positive number  such that
such that  for all
for all  , that is, if
, that is, if

By  we will denote the set of all bounded double sequences. We note that in contrast to the case for single sequences, a convergent double sequence needs not to be bounded. So, by
we will denote the set of all bounded double sequences. We note that in contrast to the case for single sequences, a convergent double sequence needs not to be bounded. So, by  we will denote the space of all real bounded and convergent double sequences.
we will denote the space of all real bounded and convergent double sequences.
Let  be a four-dimensional infinite matrix of real numbers for all
be a four-dimensional infinite matrix of real numbers for all  The sums
The sums

are called the  -transforms of the double sequence
-transforms of the double sequence  and we will denote it by
and we will denote it by  . We say that a sequence
. We say that a sequence  is
is  -summable to the limit
-summable to the limit  if the
if the  -transform of
-transform of  exists for all
exists for all  and convergent to
and convergent to  in the Pringsheim sense, that is,
in the Pringsheim sense, that is,

Móricz and Rhoades [2] have defined almost convergence of a double sequence as follows.
A double sequence  of real numbers is said to be almost convergent to a limit
of real numbers is said to be almost convergent to a limit  if
if

uniformly in  . By
. By  we denote the set of all almost convergent double sequences.
we denote the set of all almost convergent double sequences.
Recall that Knopp's Core of a single bounded sequence  is the closed interval
is the closed interval  in [3, page 138]. In the sense of Knopp's Core,
in [3, page 138]. In the sense of Knopp's Core,  -core of a double sequence was introduced by Patterson as the closed interval
-core of a double sequence was introduced by Patterson as the closed interval  in [4], where the definitions of
in [4], where the definitions of  (Pringsheim limit inferior) and
(Pringsheim limit inferior) and  (Pringsheim limit superior) are given as follows. Let
(Pringsheim limit superior) are given as follows. Let  and
and  . Then
. Then

After this definition, this concept has been studied by many authors. For example see in [5–11] and the others.
Let  denote the set of all natural numbers. A bijective function
denote the set of all natural numbers. A bijective function  is said to be a permutation. In this paper we have determined two permutations
is said to be a permutation. In this paper we have determined two permutations  and
and  for which
for which  -core
-core  -core
-core  for all
for all  .
.
A two-dimensional matrix transformation is said to be regular (see [3, page 64]) if it maps every convergent sequence into a convergent sequence with the same limit. In 1926, Robison presented a four-dimensional analogue of regularity for double sequences in which he added an additional assumption of boundedness. A four-dimensional matrix  is said to be
is said to be  -regular if it maps every bounded P-convergent sequence into a P-convergent sequence with the same P-limit.
-regular if it maps every bounded P-convergent sequence into a P-convergent sequence with the same P-limit.
The four-dimensional matrix  is bounded-regular or
is bounded-regular or  -regular if and only if
-regular if and only if

Lemma (see [4]).
If  is a four-dimensional matrix, then for all real-valued double sequences
is a four-dimensional matrix, then for all real-valued double sequences  ,
,

if and only if  is RH-regular and
is RH-regular and

Now let us state the definition given in [14] for absolutely equivalent  -regular matrices.
-regular matrices.
Definition 1.3.
Two
 -regular matrices
-regular matrices
 and
and
 are said to be absolutely equivalent for a given class of sequences
are said to be absolutely equivalent for a given class of sequences
 whenever
whenever

This means that  and
and  have the same limit or neither
have the same limit or neither  nor
nor  have a limit but their difference goes to zero.
have a limit but their difference goes to zero.
The following proposition, lemma, and theorem characterizing the relationship between absolutely equivalent matrices and the  -core are given in [14].
-core are given in [14].
Proposition 1.4.
A necessary and sufficient condition for the  -regular matrices
-regular matrices  and
and  to be absolutely equivalent for all bounded sequences is that
to be absolutely equivalent for all bounded sequences is that

Lemma.
If two double sequences  and
and  are such that
are such that  , then
, then  -core
-core  -core
-core  .
.
Theorem.

-core  -core
-core  for all bounded sequences
for all bounded sequences  if and only if
if and only if  is
is  -regular and is absolutely equivalent to a nonnegative matrix
-regular and is absolutely equivalent to a nonnegative matrix  for all bounded sequences.
for all bounded sequences.
If  , then the four-dimensional matrix
, then the four-dimensional matrix  is said to be strongly
is said to be strongly  -regular. In [2] the characterization of strongly
-regular. In [2] the characterization of strongly  -regular has been given as follows.
-regular has been given as follows.
Theorem.
A matrix  is strongly
is strongly  -regular if and only if
-regular if and only if  is
is  -regular and
-regular and

2. The Main Results
Theorem 2.1.
If  is a strongly
is a strongly  -regular matrix and
-regular matrix and  are two permutations such that
are two permutations such that

then  -core
-core  -core
-core  for all
for all  , where
, where  is a positive integer and
is a positive integer and

Proof.
In the light of Lemma 1.5, it is enough to show that  .
.
Let  and
and  . Then, it is clear that
. Then, it is clear that  for each
for each  . Now, for
. Now, for  , we can write
, we can write

On the other hand, since  is strongly
is strongly  -regular, by an easy calculation it can be seen that
-regular, by an easy calculation it can be seen that

By the same way, one can also see that

Now, conditions (1.11) imply that  This completes the proof.
This completes the proof.
Here, let us specialize the permutations  and
and  . Let
. Let  and
and  be a permutation on
be a permutation on  such that
such that  and
and

for  (see in [15, 16]). Also, let choose the permutation
(see in [15, 16]). Also, let choose the permutation  such that
such that  for all
for all  . Then, we have the following theorem.
. Then, we have the following theorem.
Theorem 2.2.
If  is a strongly
is a strongly  -regular nonnegative matrix and
-regular nonnegative matrix and  are two permutations as above, then
are two permutations as above, then  -core
-core  -core
-core  for all
for all  .
.
Proof.
By the same technique used in Theorem 2.1, one can see that  . So, Lemma 1.5 implies that
. So, Lemma 1.5 implies that  -core
-core  -core
-core  . But, since
. But, since  is an
is an  -regular nonnegative matrix,
-regular nonnegative matrix,  -core
-core  -core
-core  for all
for all  . This step completes the proof.
. This step completes the proof.
References
Pringsheim A: Zur theorie der zweifach unendlichen Zahlenfolgen. Mathematische Annalen 1900, 53(3):289–321. 10.1007/BF01448977
Móricz F, Rhoades BE: Almost convergence of double sequences and strong regularity of summability matrices. Mathematical Proceedings of the Cambridge Philosophical Society 1988, 104(2):283–294. 10.1017/S0305004100065464
Cooke RG: Infinite Matrices and Sequence Spaces. Mcmillan, New York, NY, USA; 1950.
Patterson RF: Double sequence core theorems. International Journal of Mathematics and Mathematical Sciences 1999, 22(4):785–793. 10.1155/S0161171299227858
Çakan C, Altay B, Çoşkun H: Double lacunary density and lacunary statistical convergence of double sequences. Studia Scientiarum Mathematicarum Hungarica. In press
Çakan C, Altay B, Mursaleen M: The -convergence and -core of double sequences. Applied Mathematics Letters 2006, 19(10):1122–1128. 10.1016/j.aml.2005.12.003
Çakan C, Altay B: Statistically boundedness and statistical core of double sequences. Journal of Mathematical Analysis and Applications 2006, 317(2):690–697. 10.1016/j.jmaa.2005.06.006
Çakan C, Altay B: A class of conservative four-dimensional matrices. Journal of Inequalities and Applications 2006, 2006:-8.
Mursaleen M, Edely OHH: Almost convergence and a core theorem for double sequences. Journal of Mathematical Analysis and Applications 2004, 293(2):532–540. 10.1016/j.jmaa.2004.01.015
Mursaleen M, Savaş E: Almost regular matrices for double sequences. Studia Scientiarum Mathematicarum Hungarica 2003, 40(1–2):205–212.
Mursaleen M: Almost strongly regular matrices and a core theorem for double sequences. Journal of Mathematical Analysis and Applications 2004, 293(2):523–531. 10.1016/j.jmaa.2004.01.014
Hamilton HJ: Transformations of multiple sequences. Duke Mathematical Journal 1936, 2(1):29–60. 10.1215/S0012-7094-36-00204-1
Robison GM: Divergent double sequences and series. Transactions of the American Mathematical Society 1926, 28(1):50–73. 10.1090/S0002-9947-1926-1501332-5
Patterson RF: Four dimensional matrix characterizations of the Pringsheim core. Southeast Asian Bulletin of Mathematics 2004, 27(5):899–906.
Öztürk E: On absolutely equivalent summability methods. Bulletin of the Institute of Mathematics. Academia Sinica 1985, 13(1):35–39.
Sarıgöl MA: On absolutely equivalent of summability methods. Bulletin of the Institute of Mathematics. Academia Sinica 1988, 16(1):105–108.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Furkan, H., Çakan, C. Characterization of 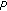 -Core and Absolute Equivalence of Double Sequences.
J Inequal Appl 2010, 432059 (2010). https://doi.org/10.1155/2010/432059
-Core and Absolute Equivalence of Double Sequences.
J Inequal Appl 2010, 432059 (2010). https://doi.org/10.1155/2010/432059
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/432059