- Research Article
- Open access
- Published:
On the Exponent of Convergence for the Zeros of the Solutions of 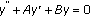
Journal of Inequalities and Applications volume 2010, Article number: 428936 (2010)
Abstract
Let  and
and  be entire functions of order less than 1 with
be entire functions of order less than 1 with  and
and  transcendental. We prove that every solution
transcendental. We prove that every solution  of the equation
of the equation  ,
,  ,
, 
 being has zeros with infinite exponent of convergence.
being has zeros with infinite exponent of convergence.
1. Introduction
It is assumed that the reader of this paper is familiar with the basic concepts of Nevanlinna theory [1, 2] such as  , and
, and  . Suppose that
. Suppose that  is a meromorphic function, then the order of growth of the function
is a meromorphic function, then the order of growth of the function  and the exponent of convergence of the zeros of
and the exponent of convergence of the zeros of  are defined, respectively, as
are defined, respectively, as

Let  be a measurable subset of
be a measurable subset of  . The lower logarithmic density and the upper logarithmic density of
. The lower logarithmic density and the upper logarithmic density of  are defined, respectively, by
are defined, respectively, by

where  is the characteristic function of
is the characteristic function of  defined as
defined as

Now let us recall some of the previous results on the linear differential equation

where  is an entire function of finite order, When
is an entire function of finite order, When  is polynomial, many authors [3–6] have studied the properties of the solutions of (1.4). If
is polynomial, many authors [3–6] have studied the properties of the solutions of (1.4). If  is a transcendental entire function with
is a transcendental entire function with  , Gundersen [7] proved that every nontrivial solution of (1.4) has infinite order of growth. In [8], Wang and Laine considered the nonhomogeneous equation of type
, Gundersen [7] proved that every nontrivial solution of (1.4) has infinite order of growth. In [8], Wang and Laine considered the nonhomogeneous equation of type

where  are entire functions of order less than one and
are entire functions of order less than one and  are complex numbers. In fact, they have proved the following theorem.
are complex numbers. In fact, they have proved the following theorem.
Theorem 1.1.
Suppose that  are entire functions of order less than one, and suppose that
are entire functions of order less than one, and suppose that  with
with  and
and  . Then every nontrivial solution of (1.5) is of infinite order.
. Then every nontrivial solution of (1.5) is of infinite order.
Corollary 1.2.
Suppose that  , where
, where  is a nonvanishing entire function with
is a nonvanishing entire function with  and
and  with
with  . Then every nontrivial solution of (1.4) is of infinite order.
. Then every nontrivial solution of (1.4) is of infinite order.
2. Results
We observe that all the above results concern the order of growth only. In this paper, we are going to prove the following theorem which concerns the exponent of convergence.
Theorem 2.1.
Let  and
and  be entire functions of order less than 1 with
be entire functions of order less than 1 with  and
and  being transcendental. Then every solution
being transcendental. Then every solution  of the equation
of the equation

has zeros with infinite exponent of convergence.
The hypothesis that  is transcendental is not redundant since Frei [4] has shown that
is transcendental is not redundant since Frei [4] has shown that

has solutions of finite order, for certain constants  .
.
We notice that Theorem 2.1 fails for  . For any entire function
. For any entire function  the function
the function  solves (2.1) with
solves (2.1) with

3. Some Lemmas
Throughout this paper we need the following lemmas. In 1965, Hayman [9] proved the following lemma.
Lemma 3.1.
Let the function  be meromorphic of finite order
be meromorphic of finite order  in the plane and let
in the plane and let  . Then
. Then

for all  outside a set
outside a set  of upper logarithmic density
of upper logarithmic density  , where the positive constant
, where the positive constant  depends only on
depends only on  and
and  .
.
In 1962, Edrei and Fuchs [10] proved the following lemma.
Lemma 3.2.
Let  be a meromorphic function in the complex plane and let
be a meromorphic function in the complex plane and let  have measure
have measure  . Then
. Then

In 2007, Bergweiler and Langley [11] proved the following lemma.
Lemma 3.3.
Let  be a transcendental entire function of order
be a transcendental entire function of order  . For large
. For large  define
define  to be the length of the longest arc of the circle
to be the length of the longest arc of the circle  on which
on which  , with
, with  if the minimum modulus
if the minimum modulus  satisfies
satisfies  . Then at least one of the following is true:
. Then at least one of the following is true:
(i)there exists a set  of positive upper logarithmic density such that
of positive upper logarithmic density such that  for
for  ;
;
(ii)for each  the set
the set  has lower logarithmic density at least
has lower logarithmic density at least 
We deduce the following.
Lemma 3.4.
Let  , let
, let  be a positive integer, and let
be a positive integer, and let  have logarithmic density
have logarithmic density  . Let
. Let  be a transcendental entire function such that
be a transcendental entire function such that  on a path
on a path  tending to infinity and for all
tending to infinity and for all  with
with  and
and  . Then
. Then  has order at least
has order at least  .
.
Proof.
Assume that  and choose a polynomial
and choose a polynomial  of degree at most
of degree at most  such that
such that

is transcendental entire. Then we have  for all
for all  and for all
and for all  with
with  and
and  . With the notation of Lemma 3.3, we see that
. With the notation of Lemma 3.3, we see that  for all large
for all large  , and so we must have case (ii), as well as
, and so we must have case (ii), as well as  for
for  . Define
. Define  by
by

Since  has logarithmic density
has logarithmic density  this gives
this gives

4. Proof of Theorem 2.1
Let  ,
,  and
and  be as in the hypotheses. We can assume that
be as in the hypotheses. We can assume that  . Suppose that
. Suppose that  is a solution of (2.1) having zeros with finite exponent of convergence. Then we can write
is a solution of (2.1) having zeros with finite exponent of convergence. Then we can write

where  and
and  are entire functions with
are entire functions with  . We can assume that
. We can assume that  , since if
, since if  is constant we can replace
is constant we can replace  by
by  and
and  by
by  . Using (2.1) and (4.1), we get
. Using (2.1) and (4.1), we get

Lemma 4.1.
One has  .
.
Proof.
Suppose that  . Dividing (4.2) by
. Dividing (4.2) by  , we get
, we get

Hence, provided  lies outside a set of finite measure,
lies outside a set of finite measure,

and so, using the fact that  and
and  have order less than
have order less than  , we obtain
, we obtain

This holds outside a set  of finite measure and so for all large
of finite measure and so for all large  , since we may take
, since we may take  with
with  so that
so that

Lemma 4.1 is proved.
Let  denote large positive constants. Choose
denote large positive constants. Choose  with
with

There exists an  -set
-set  [2, page 84] such that for all large
[2, page 84] such that for all large  outside
outside  , we have
, we have

and using the Poisson-Jensen formula,

Moreover, there exists a set  of logarithmic density
of logarithmic density  such that for
such that for  the circle
the circle  does not meet the
does not meet the  -set
-set  .
.
Lemma 4.2.
The functions  and
and  are both transcendental.
are both transcendental.
Proof.
Let  be small and positive and suppose that
be small and positive and suppose that  or
or  is a polynomial. Let
is a polynomial. Let  be large with
be large with  and
and  . Since
. Since  is small it follows from (4.2) and (4.8) that
is small it follows from (4.2) and (4.8) that  . Choose
. Choose  with
with  such that the intersection of
such that the intersection of  with the ray
with the ray  given by
given by  is bounded. Applying Lemma 3.4 to the function
is bounded. Applying Lemma 3.4 to the function  , with
, with  a subpath of
a subpath of  , gives
, gives  , but
, but  may be chosen arbitrarily small, and this contradicts (4.7).
may be chosen arbitrarily small, and this contradicts (4.7).
The next step is to estimate  in the right half-plane.
in the right half-plane.
Lemma 4.3.
Let  be a large positive integer and let
be a large positive integer and let  . Then for large
. Then for large  with
with

one has, either

or

Proof.
Let  be large and satisfy (4.10), and assume that (4.11) does not hold. Then (4.8) implies that
be large and satisfy (4.10), and assume that (4.11) does not hold. Then (4.8) implies that

Also, (4.7), and (4.9) give

Here  denote positive constants which may depend on
denote positive constants which may depend on  but not on
but not on  . Using (4.8), (4.12) and (4.14) we get, from (4.2),
. Using (4.8), (4.12) and (4.14) we get, from (4.2),

Now divide (4.2) by  . We obtain, using (4.15),
. We obtain, using (4.15),

which gives  and (4.12). This proves Lemma 4.3.
and (4.12). This proves Lemma 4.3.
Lemma 4.4.
Let  and
and  be as in Lemma 4.3. Choose
be as in Lemma 4.3. Choose  such that the ray
such that the ray  has bounded intersection with the
has bounded intersection with the  -set
-set  . Let
. Let  be the union of the ray
be the union of the ray  and the arcs
and the arcs  , where
, where  is the set chosen following (4.9). Then one of the following holds:
is the set chosen following (4.9). Then one of the following holds:
(i)one has (4.11) for all large  in
in  ;
;
(ii)one has (4.12) for all large  in
in  .
.
Proof.
This follows simply from continuity. For each large  in
in  we have (4.11) or (4.12), but we cannot have both because of (4.14). This proves Lemma 4.4.
we have (4.11) or (4.12), but we cannot have both because of (4.14). This proves Lemma 4.4.
Lemma 4.5.
Let  . Then for large
. Then for large  with
with  , one has
, one has

Proof.
Let  be as in the hypotheses. Since
be as in the hypotheses. Since  we only need to prove (4.17) for
we only need to prove (4.17) for  . Assume that
. Assume that  . Then dividing (4.2) by
. Then dividing (4.2) by  gives
gives

by (4.8), and so (4.17) follows using (4.7). This proves Lemma 4.5.
Lemma 4.6.
If conclusion (i) of Lemma 4.4 holds then  , while if conclusion (ii) of Lemma 4.4 holds then
, while if conclusion (ii) of Lemma 4.4 holds then  .
.
Proof.
Suppose that conclusion (i) of Lemma 4.4 holds. Choose  such that
such that

and let  be small compared to
be small compared to  . Assume that
. Assume that  in Lemma 4.4 is small compared to
in Lemma 4.4 is small compared to  , in particular so small that
, in particular so small that

where  is the positive constant from Lemma 3.1. Let
is the positive constant from Lemma 3.1. Let

and let  be the exceptional set of Lemma 3.1, with
be the exceptional set of Lemma 3.1, with  . Then for large
. Then for large  we have, using (4.20) and Lemmas 3.1, 3.2, and 4.5,
we have, using (4.20) and Lemmas 3.1, 3.2, and 4.5,

We then have

for large  . Now take any large
. Now take any large  . Since
. Since  has logarithmic density
has logarithmic density  , while
, while  has upper logarithmic density at most
has upper logarithmic density at most  , and since
, and since  is small, there exists
is small, there exists  with
with

which proves Lemma 4.6 in this case. The alternative case, in which we have conclusion (ii) in Lemma 4.4, is proved the same way, using  in place of
in place of  .
.
To finish the proof suppose first that conclusion (ii) of Lemma 4.4 holds. Then Lemma 3.4 implies that  has order at least
has order at least  . Since
. Since  may be chosen arbitrarily small, this contradicts Lemma 4.6. The same contradiction, with
may be chosen arbitrarily small, this contradicts Lemma 4.6. The same contradiction, with  replaced by
replaced by  , arises if conclusion (i) of Lemma 4.4 holds, and the proof of the theorem is complete.
, arises if conclusion (i) of Lemma 4.4 holds, and the proof of the theorem is complete.
References
Hayman WK: Meromorphic Functions, Oxford Mathematical Monographs. Clarendon Press, Oxford, UK; 1964:xiv+191.
Laine I: Nevanlinna Theory and Complex Differential Equations, de Gruyter Studies in Mathematics. Volume 15. W. de Gruyter, Berlin, Germany; 1993:viii+341.
Amemiya I, Ozawa M: Nonexistence of finite order solutions of . Hokkaido Mathematical Journal 1981, 10: 1–17.
Frei M: Über die subnormalen Lösungen der Differentialgleichung (Konst.) . Commentarii Mathematici Helvetici 1961, 36: 1–8.
Langley JK: On complex oscillation and a problem of Ozawa. Kodai Mathematical Journal 1986, 9(3):430–439. 10.2996/kmj/1138037272
Ozawa M: On a solution of . Kodai Mathematical Journal 1980, 3(2):295–309. 10.2996/kmj/1138036197
Gundersen GG: On the question of whether can admit a solution of finite order. Proceedings of the Royal Society of Edinburgh. Section A 1986, 102(1–2):9–17. 10.1017/S0308210500014451
Wang J, Laine I: Growth of solutions of second order linear differential equations. Journal of Mathematical Analysis and Applications 2008, 342(1):39–51.
Hayman WK: On the characteristic of functions meromorphic in the plane and of their integrals. Proceedings of the London Mathematical Society. Third Series 1965, 3(14):93–128.
Edrei A, Fuchs WHJ: Bounds for the number of deficient values of certain classes of meromorphic functions. Proceedings of the London Mathematical Society. Third Series 1962, 12: 315–344. 10.1112/plms/s3-12.1.315
Bergweiler W, Langley JK: Zeros of differences of meromorphic functions. Mathematical Proceedings of the Cambridge Philosophical Society 2007, 142(1):133–147. 10.1017/S0305004106009777
Acknowledgment
The author thanks Professor J. K. Langley for the invaluable discussions on the results of this paper during his visit in summer 2008 and summer 2010 to the University of Nottingham in the U.K.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Alotaibi, A. On the Exponent of Convergence for the Zeros of the Solutions of 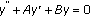 .
J Inequal Appl 2010, 428936 (2010). https://doi.org/10.1155/2010/428936
.
J Inequal Appl 2010, 428936 (2010). https://doi.org/10.1155/2010/428936
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/428936