- Research Article
- Open access
- Published:
A New Hilbert-Type Linear Operator with a Composite Kernel and Its Applications
Journal of Inequalities and Applications volume 2010, Article number: 393025 (2010)
Abstract
A new Hilbert-type linear operator with a composite kernel function is built. As the applications, two new more accurate operator inequalities and their equivalent forms are deduced. The constant factors in these inequalities are proved to be the best possible.
1. Introduction
In 1908, Weyl [1] published the well-known Hilbert's inequality as follows:
if  ,
,  are real sequences,
are real sequences,  and
and  , then
, then

where the constant factor  is the best possible.
is the best possible.
Under the same conditions, there are the classical inequalities [2]


where the constant factors  and
and  are the best possible also. Expression (1.2) is called a more accurate form of(1.1). Some more accurate inequalities were considered by [3–5]. In 2009, Zhong [5] gave a more accurate form of (1.3).
are the best possible also. Expression (1.2) is called a more accurate form of(1.1). Some more accurate inequalities were considered by [3–5]. In 2009, Zhong [5] gave a more accurate form of (1.3).
Set  ,
,  as two pairs of conjugate exponents, and
as two pairs of conjugate exponents, and  ,
,  ,
,  , and
, and  ,
,  , such that
, such that  and
and  , then it has
, then it has

Letting  ,
,  ,
,  ,
,  ,
,  , and
, and  , the expression (1.4) can be rewritten as
, the expression (1.4) can be rewritten as

where  is a linear operator,
is a linear operator,  .
.  is the norm of the sequence
is the norm of the sequence  with a weight function
with a weight function  .
.  is a formal inner product of the sequences
is a formal inner product of the sequences  and
and  .
.
By setting two monotonic increasing functions  and
and  , a new Hilbert-type inequality, which is with a composite kernel function
, a new Hilbert-type inequality, which is with a composite kernel function  , and its equivalent are built in this paper. As the applications, two new more accurate Hilbert-type inequalities incorporating the linear operator and the norm are deduced.
, and its equivalent are built in this paper. As the applications, two new more accurate Hilbert-type inequalities incorporating the linear operator and the norm are deduced.
Firstly, the improved Euler-Maclaurin's summation formula [6] is introduced.
Set  . If
. If 
 ,
,  (
( ), then it has
), then it has

2. Lemmas
Lemma 2.1.
Set  as a pair of conjugate exponents,
as a pair of conjugate exponents,  ,
,  ,
,  , and define
, and define





Then, it has the following.
(1)The functions  ,
,  satisfy the conditions of (1.6). It means that
satisfy the conditions of (1.6). It means that

(2)

(3)

Proof.
-
(1)
For
 ,
,  ,
, 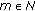 ,
, 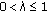 , and
, and  , set
, set  (2.9)
(2.9)
It has

when  . It is easy to find that
. It is easy to find that

Similarly, it can be shown that  ,
,  (
( ,
,  ). These tell us that (2.6) holds and the functions
). These tell us that (2.6) holds and the functions  ,
,  satisfy the conditions of (1.6).
satisfy the conditions of (1.6).
-
(2)
Set
 . With the partial integration, it has
. With the partial integration, it has  (2.12)
(2.12)
By (2.1), it has


In view of (2.12)~(2.14), it has

As  ,
,  , and
, and  , it has
, it has

It means that  . Similarly, it can be shown that
. Similarly, it can be shown that  . The expression (2.7) holds.
. The expression (2.7) holds.
-
(3)
By (2.5), (2.12), (2.13), and
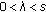 ,
, 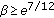 , it has
, it has  (2.17)
(2.17)
The expression (2.8) holds, and Lemma 2.1 is proved.
Lemma 2.2.
Set  as a pair of conjugate exponents,
as a pair of conjugate exponents,  ,
,  , and
, and  , and define
, and define

Then, it has
(1)The functions  ,
,  satisfy the conditions of (1.6). It means that
satisfy the conditions of (1.6). It means that

(2)

(3)

Proof.
-
(1)
Letting
 ,
, 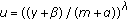 , it can be proved that
, it can be proved that 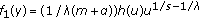 satisfy (2.19) as in [5]. Similarly, it can be shown that
satisfy (2.19) as in [5]. Similarly, it can be shown that 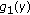 satisfy (2.19) also.
satisfy (2.19) also. -
(2)
Setting
 , by
, by 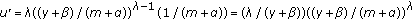 ,
, , and
, and 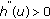 , it has
, it has 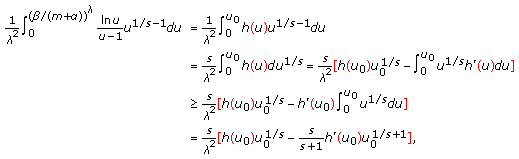 (2.22)
(2.22)


With (2.22)~(2.24), it has

By  ,
,  , and
, and  ,
,  ,
,  , it has
, it has

So  holds. Similarly, it can be shown that
holds. Similarly, it can be shown that  .
.
-
(3)
In view of (2.22), (2.23), by
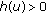 ,
, 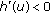 , it has
, it has 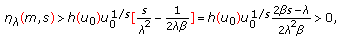 (2.27)
(2.27)
and by  , so there exists a constant
, so there exists a constant  , such that
, such that  (
( ). Then it has
). Then it has

It means that (2.21) holds. The proof for Lemma 2.2 is finished.
3. Main Results
Set  ,
,  ,
, ,
, , and
, and  as two pairs of conjugate exponents.
as two pairs of conjugate exponents.  is a measurable kernel function. Both
is a measurable kernel function. Both  and
and  are strictly monotonic increasing differentiable functions in
are strictly monotonic increasing differentiable functions in  such that
such that  ,
, . Give some notations as follows:
. Give some notations as follows:
-
(1)
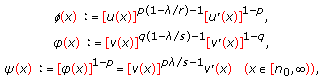 (3.1)
(3.1)
(2) set
set

and call  a real space of sequences, where
a real space of sequences, where

is called the norm of the sequence with a weight function . Similarly, the real spaces of sequences
. Similarly, the real spaces of sequences ,
, and the norm
and the norm can be defined as well,
can be defined as well,
-
(3)
define a Hilbert-type linear operator
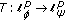 , for all
, for all  ,
,

-
(4)
for all
 ,
,  , define the formal inner product of
, define the formal inner product of and
and as
as

define two weight coefficients and
and  as
as

Then it has some results in the following theorems.
Theorem 3.1.
Suppose that  ,
,  , and
, and  . If there exists a positive number
. If there exists a positive number  , such that
, such that


then for all  and
and  , it has the following:
, it has the following:
(1)

It means that  ,
,
(2) is a bounded linear operator and
is a bounded linear operator and

where  ,
,  are defined by (3.4),
are defined by (3.4),  is defined as (3.3).
is defined as (3.3).
Proof.
By using Hölder's inequality [7] and (3.6), (3.7), it has  and
and

And by  , it follows that
, it follows that

This means that  ,
,  , and
, and  .
.  is a bounded linear operator.
is a bounded linear operator.
If there exists a constant  , such that
, such that  , then for
, then for  , setting
, setting  ,
,  , it has
, it has  ,
,  , and
, and

But on the other side, by (3.8), it has

By the strictly monotonic increase of  and
and  ,
,  , there exists
, there exists  such that
such that  for all
for all  . So it has
. So it has

The series is uniformly convergent for  , so it has
, so it has

and for  , there exists
, there exists  , when
, when  , it has
, it has

By (3.14) and (3.8), when  , it has
, it has

In view of (3.13) and (3.18), letting  , it has
, it has  . This means that
. This means that  ; that is,
; that is,  . Theorem 3.1 is proved.
. Theorem 3.1 is proved.
Theorem 3.2.
Suppose that  and
and  are two pairs of conjugate exponents,
are two pairs of conjugate exponents,  ,
,  ,
,  . Let
. Let

Here,  ,
,  satisfy the conditions as in Theorem 3.1. Set
satisfy the conditions as in Theorem 3.1. Set



If (a)  is a homogeneous measurable kernel function of "
is a homogeneous measurable kernel function of " '' degree in
'' degree in  , such that
, such that

-
(b)
functions
 ,
, 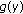 satisfy the conditions of (1.6); that is,
satisfy the conditions of (1.6); that is, 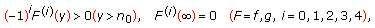 (3.24)
(3.24)
-
(c)
there exists
 , such that
, such that  (3.25)
(3.25)
then it has
(1)if  ,
,  , and
, and  ,
,  , then
, then

(2)if  and
and  , then
, then

where inequality (3.27) is equivalent to (3.26) and the constant factor  is the best possible.
is the best possible.
Proof.
By (3.24), (1.6), it has


Letting  and
and  in the integral of (3.28) and (3.29), respectively, by (3.23), it has
in the integral of (3.28) and (3.29), respectively, by (3.23), it has


(where, letting  , it has
, it has  ). In view of (3.28), (3.30), (3.20), (3.22), and with (3.25), it has
). In view of (3.28), (3.30), (3.20), (3.22), and with (3.25), it has

Similarly, with (3.29), (3.31), (3.21), and (3.25), it has

also. By Theorem 3.1, it has

and (3.27) holds. In view of

(3.26) holds also.
If (3.26) holds, from (3.26) and  , there exists
, there exists  , such that
, such that  and
and  when
when  . For
. For  , it has
, it has

By  and
and  , it follows that
, it follows that

Letting  in (3.37), it has
in (3.37), it has  , and it means that
, and it means that  and
and  . Therefore, the inequality (3.36) keeps the form of the strict inequality when
. Therefore, the inequality (3.36) keeps the form of the strict inequality when  . In view of
. In view of  , inequality (3.27) holds and (3.27) is equivalent to (3.26). By
, inequality (3.27) holds and (3.27) is equivalent to (3.26). By  , it is obvious that the constant factor
, it is obvious that the constant factor  is the best possible. This completes the proof of Theorem 3.2.
is the best possible. This completes the proof of Theorem 3.2.
4. Applications
Example 4.1.
Set  ,
,  be two pairs of conjugate exponents and
be two pairs of conjugate exponents and  ,
,  ,
,  ,
,  . Then it has the following.
. Then it has the following.
(1)If  , and
, and  , then
, then

(2)If  , then
, then

where the constant factors  and
and  are both the best possible. Inequality (4.2) is equivalent to (4.1).
are both the best possible. Inequality (4.2) is equivalent to (4.1).
Proof.
Setting  ,
,  , it is a homogeneous measurable kernel function of "
, it is a homogeneous measurable kernel function of " '' degree. Letting
'' degree. Letting  , it has
, it has

Setting  ,
,  , then both
, then both  and
and  are strictly monotonic increasing differentiable functions in
are strictly monotonic increasing differentiable functions in  and satisfy
and satisfy

for  . As
. As  ,
,  ,
,  , and
, and  , letting
, letting

with (2.1)~(2.8), it has

When  and
and  ; that is,
; that is,  ,
,  and
and  ,
,  , by Theorem 3.2, inequality (4.1) holds, so does (4.2). And (4.2) is equivalent to (4.1), and the constant factors
, by Theorem 3.2, inequality (4.1) holds, so does (4.2). And (4.2) is equivalent to (4.1), and the constant factors  and
and  are both the best possible.
are both the best possible.
Example 4.2.
Set  ,
,  be two pairs of conjugate exponents and
be two pairs of conjugate exponents and  ,
,  ,
,  ,
,  . Then it has the following.
. Then it has the following.
(1)If  and
and  , then
, then

(2)If  , then
, then

where inequality (4.8) is equivalent to (4.7) and the constant factors  and
and  are both the best possible.
are both the best possible.
Proof.
Setting 
 , it is a homogeneous measurable kernel function of "
, it is a homogeneous measurable kernel function of " '' degree. Letting
'' degree. Letting  , it has [2]
, it has [2]

Setting  ,
,  , then both
, then both  and
and  are strictly monotonic increasing differentiable functions in
are strictly monotonic increasing differentiable functions in  and satisfy
and satisfy

for  . As
. As  ,
,  ,
,  , and
, and  , letting
, letting

with (2.18)~(2.21), it has

When  and
and  ; that is,
; that is,  ,
,  and
and  ,
,  , by Theorem 3.2, inequality (4.7) holds, so does (4.8). And (4.8) is equivalent to (4.7), and the constant factors
, by Theorem 3.2, inequality (4.7) holds, so does (4.8). And (4.8) is equivalent to (4.7), and the constant factors  and
and  are both the best possible.
are both the best possible.
Remark 4.3.
It can be proved similarly that, if the conditions " " in Lemma 2.1 and "
" in Lemma 2.1 and " " in Lemma 2.2 are changed into "
" in Lemma 2.2 are changed into " " and "
" and " ", respectively, Lemmas 2.1 and 2.2 are also valid. So the conditions "
", respectively, Lemmas 2.1 and 2.2 are also valid. So the conditions " " in Example 4.1 and "
" in Example 4.1 and " " in Example 4.2 can be replaced by "
" in Example 4.2 can be replaced by " ,
,  " and "
" and " ,
,  ", respectively.
", respectively.
References
Weyl H: Singulare Integralgleichungen mit besonderer Beriicksichtigung des Fourierschen Integraltheorems, Inaugeral dissertation. University of Göttingen, Göttingen, Germany; 1908.
Hardy G, Littiewood J, Polya G: Inequalities. Cambridge University Press, Cambridge, UK; 1934.
Yang BC: On a more accurate Hardy-Hilbert-type inequality and its applications. Acta Mathematica Sinica 2006, 49(2):363–368.
Yang B: On a more accurate Hilbert's type inequality. International Mathematical Forum 2007, 2(37–40):1831–1837.
Zhong W: A Hilbert-type linear operator with the norm and its applications. Journal of Inequalities and Applications 2009, 2009:-18.
Yang B: The Norm of Operator and Hilbert-Type Inequalities. Science Press, Beijing, China; 2009.
Kuang J: Applied Inequalities. Shangdong Science and Technology Press, Jinan, China; 2004.
Acknowledgment
This paper is supported by the National Natural Science Foundation of China (no. 10871073). The author would like to thank the anonymous referee for his or her suggestions and corrections.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhong, W. A New Hilbert-Type Linear Operator with a Composite Kernel and Its Applications. J Inequal Appl 2010, 393025 (2010). https://doi.org/10.1155/2010/393025
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/393025
 ,
,  ,
, 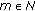 ,
, 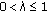 , and
, and  , set
, set 
 . With the partial integration, it has
. With the partial integration, it has 
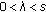 ,
, 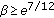 , it has
, it has 
 ,
, 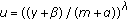 , it can be proved that
, it can be proved that 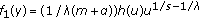 satisfy (2.19) as in [
satisfy (2.19) as in [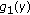 satisfy (2.19) also.
satisfy (2.19) also. , by
, by 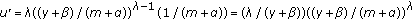 ,
, , and
, and 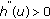 , it has
, it has 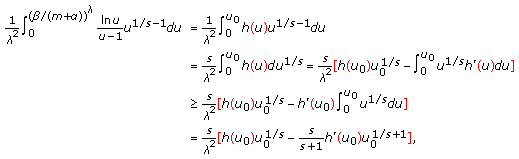
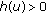 ,
, 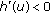 , it has
, it has 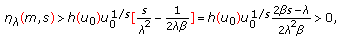
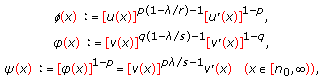
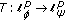 , for all
, for all  ,
,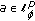 ,
,  , define the formal inner product of
, define the formal inner product of and
and as
as ,
, 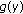 satisfy the conditions of (1.6); that is,
satisfy the conditions of (1.6); that is, 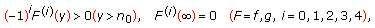
 , such that
, such that 