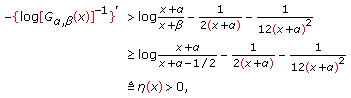- Research Article
- Open access
- Published:
A Class of Logarithmically Completely Monotonic Functions Associated with a Gamma Function
Journal of Inequalities and Applications volume 2010, Article number: 392431 (2010)
Abstract
We show that the function  is strictly logarithmically completely monotonic on
is strictly logarithmically completely monotonic on  if and only if
if and only if  and
and  is strictly logarithmically completely monotonic on
is strictly logarithmically completely monotonic on  if and only if
if and only if  .
.
1. Introduction
For real and positive values of  the Euler gamma function
the Euler gamma function  and its logarithmic derivative
and its logarithmic derivative  , the so-called digamma function, are defined as
, the so-called digamma function, are defined as

For extension of these functions to complex variables and for basic properties, see [1]. These functions play central roles in the theory of special functions and have lots of extensive applications in many branches, for example, statistics, physics, engineering, and other mathematical sciences. Over the past half century monotonicity properties of these functions have attracted the attention of many authors (see [2–22]).
Recall that a real-valued function  is said to be completely monotonic on
is said to be completely monotonic on  if
if  has derivatives of all orders on
has derivatives of all orders on  and
and

for all  and
and  . Moreover,
. Moreover,  is said to be strictly completely monotonic if inequality (1.2) is strict.
is said to be strictly completely monotonic if inequality (1.2) is strict.
Recall also that a positive real-valued function  is said to be logarithmically completely monotonic on
is said to be logarithmically completely monotonic on  if
if  has derivatives of all orders on
has derivatives of all orders on  and its logarithm
and its logarithm  satisfies
satisfies

for all  and
and  . Moreover,
. Moreover,  is said to be strictly logarithmically completely monotonic if inequality (1.3) is strict.
is said to be strictly logarithmically completely monotonic if inequality (1.3) is strict.
Recently, the completely monotonic or logarithmically completely monotonic functions have been the subject of intensive research. In particular, many remarkable results for the complete monotonicity or logarithmically complete monotonicity involving the gamma, psi and polygamma functions can be found in the literature [18, 19, 23–42].
The Kershaw's inequality in [21] states that the double inequality

holds for  and
and  . In [43], Laforgia extends the both sides of inequality in (1.4) as follows:
. In [43], Laforgia extends the both sides of inequality in (1.4) as follows:

for  or
or  and
and  , and inequality (1.5) is reversed for
, and inequality (1.5) is reversed for  and
and  .
.
Let us define

for  with
with  and
and  . In order to establish the best bounds in Kershaw's inequality (1.4), the following monotonicity and convexity properties of
. In order to establish the best bounds in Kershaw's inequality (1.4), the following monotonicity and convexity properties of  are established in [13, 44, 45]: the function
are established in [13, 44, 45]: the function  is either convex and decreasing for
is either convex and decreasing for  or concave and increasing for
or concave and increasing for  .
.
This work is motivated by an paper of Guo [46], who proved that the function

is strictly logarithmically concave and strictly increasing from  onto
onto  . It is natural to ask for an extension of this result: is
. It is natural to ask for an extension of this result: is  logarithmically complete monotonic? We will give the positive answer. Actually, we investigate a more general problem. The goal of this article is to discuss the logarithmically complete monotonicity properties of the functions
logarithmically complete monotonic? We will give the positive answer. Actually, we investigate a more general problem. The goal of this article is to discuss the logarithmically complete monotonicity properties of the functions

on  and
and  for fixed
for fixed  .
.
Recently Chen et al. [38, Theorem 1] proved the following result: let  and
and  be real numbers, define for
be real numbers, define for  ,
,

Then, the function  is strictly logarithmically completely monotonic on
is strictly logarithmically completely monotonic on  if and only if
if and only if  . So is the function
. So is the function  if and only if
if and only if  .
.
Our main results are summarized as follows.
Theorem 1.1.
Let  ,
,  , and
, and  is defined as (1.8), then
is defined as (1.8), then
(1) is strictly logarithmically completely monotonic on
is strictly logarithmically completely monotonic on  if and only if
if and only if  ;
;
(2) is strictly logarithmically completely monotonic on
is strictly logarithmically completely monotonic on  if and only if
if and only if  .
.
As applications of Theorem 1.1, one has the following corollaries.
Corollary 1.2.
For  and
and  , one has the double inequalities for the ratio of the gamma functions
, one has the double inequalities for the ratio of the gamma functions

In particular, one has

for  and
and  , and
, and

for  and
and  .
.
Corollary 1.3.
For  and
and  , one has the following double inequality
, one has the following double inequality

where  .
.
2. Lemmas
In order to prove our Theorem 1.1, we need serval lemmas which we collect in this section. In our second lemma we present the area of  to determine positive (or negative) for a function, which plays a crucial role in the proof of our result Theorem 1.1 given in Section 3.
to determine positive (or negative) for a function, which plays a crucial role in the proof of our result Theorem 1.1 given in Section 3.
Let  be a function defined on
be a function defined on  as
as

We will discuss the properties for this function and refer to view Figure 1 more clearly.
The function  can be interpreted as a quadric equation with respect to
can be interpreted as a quadric equation with respect to  , that is
, that is

where  ,
,  ,
,  and its discriminant function
and its discriminant function

Obviously, if  , then
, then  . It follows from
. It follows from  that
that  .
.
If  , then
, then  . We can solve two roots of the equation
. We can solve two roots of the equation  , which are
, which are

It follows from the properties of the quadratic equation that  for
for  and
and  for
for  or
or  .
.
Differentiating  with respect to
with respect to  , one has
, one has

By (2.5) we know that the minimal value of  can be attained at
can be attained at  , that is
, that is  . Moreover,
. Moreover,  is strictly decreasing on
is strictly decreasing on  and strictly increasing on
and strictly increasing on  .
.
Obviously,  is strictly increasing on
is strictly increasing on  . Note that
. Note that

as  . In other words,
. In other words,  and
and  has the asymptotic line
has the asymptotic line  .
.
Lemma 2.1.
The psi or digamma function, the logarithmic derivative of the gamma function, and the polygamma functions can be expressed as


for  and
and  , where
, where  is Euler's constant.
is Euler's constant.
Lemma 2.2.
Let  and
and  . Then the following statements are true:
. Then the following statements are true:
(1)if  , then
, then  for
for  ;
;
(2)if  , then
, then  for
for  ;
;
(3)if  and
and  , then there exist
, then there exist  such that
such that  for
for  and
and  for
for  .
.
Proof.
Let  and
and  . Then simple computations lead to
. Then simple computations lead to







-
(1)
If
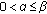 , then we divide the proof into two cases.
, then we divide the proof into two cases.
Case 1.
If  , then
, then  implies that
implies that  for
for  and
and  for
for  . Thus
. Thus  is strictly increasing on
is strictly increasing on  and strictly decreasing on
and strictly decreasing on  . From (2.10) and
. From (2.10) and  we clearly see that there exists
we clearly see that there exists  such that
such that  for
for  and
and  for
for  , which implies that
, which implies that  is strictly increasing on
is strictly increasing on  and strictly decreasing on
and strictly decreasing on  . It follows from (2.9) that
. It follows from (2.9) that

for  .
.
Case 2.
If  , then we know
, then we know  since
since  . It follows from (2.13) and (2.15) that
. It follows from (2.13) and (2.15) that

Therefore, there exists  such that
such that  for
for  and
and  for
for  follows from (2.17), which implies that
follows from (2.17), which implies that  is strictly decreasing on
is strictly decreasing on  and strictly increasing on
and strictly increasing on  . It follows from (2.12) and
. It follows from (2.12) and  that there exists
that there exists  such that
such that  for
for  and
and  for
for  . By the same argument, it follows from (2.10) and
. By the same argument, it follows from (2.10) and  that there exists
that there exists  such that
such that  for
for  and
and  for
for  .
.
Therefore,  for
for  follows from (2.9).
follows from (2.9).
-
(2)
If
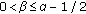 , then from Figure 1 we know that
, then from Figure 1 we know that  could be positive or negative. We divide the proof into two cases.
could be positive or negative. We divide the proof into two cases.
Case 1.
If  , then from (2.13) and (2.15) we clearly know that
, then from (2.13) and (2.15) we clearly know that  for
for  , which implies that
, which implies that  is strictly increasing on
is strictly increasing on  . Then the properties of
. Then the properties of  and
and  lead to
lead to

It follows from (2.12) and (2.18) that there exists  such that
such that  for
for  and
and  for
for  since
since  as
as  . Hence
. Hence  is strictly decreasing on
is strictly decreasing on  and strictly increasing on
and strictly increasing on  . From (2.10) and
. From (2.10) and  we know that there exists
we know that there exists  such that
such that  for
for  and
and  for
for  . Therefore, it follows from (2.9) that
. Therefore, it follows from (2.9) that

for  .
.
Case 2.
If  , then from (2.13) and (2.15) we know that there exists
, then from (2.13) and (2.15) we know that there exists  such that
such that  for
for  and
and  for
for  . Thus
. Thus  is strictly decreasing on
is strictly decreasing on  and strictly increasing on
and strictly increasing on  . It follows from (2.12) and
. It follows from (2.12) and  that there exists
that there exists  such that
such that  for
for  and
and  for
for  . By the same argument as Case 1,
. By the same argument as Case 1,  for
for  follows from (2.9) and (2.10).
follows from (2.9) and (2.10).
-
(3)
If
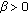 and
and 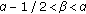 , then from (2.12) we clearly know that
, then from (2.12) we clearly know that  . Thus there exists
. Thus there exists  such that
such that 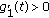 for
for  . It follows from (2.10) that
. It follows from (2.10) that  ,
, 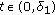 . Since
. Since  as
as 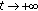 , we know that there exists
, we know that there exists 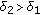 such that
such that 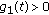 for
for  , which implies that
, which implies that 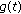 is strictly increasing on
is strictly increasing on  and
and 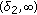 . Therefore,
. Therefore, 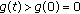 for
for 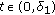 and
and 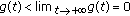 for
for 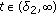 .
.
We state a simple lemma as the results of [12, 47].
Lemma 2.3.
Inequality

holds for  .
.
3. Proof of Theorem 1.1
Proof of Theorem 1.1.
Taking the logarithm of (1.8) and differentiating, then we have

For  , it follows from (2.8) that
, it follows from (2.8) that

where

-
(1)
If
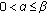 , then it follows from (3.1) and (2.20) that
, then it follows from (3.1) and (2.20) that 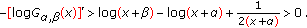 (3.4)
(3.4)
From (3.2) and (3.3) together with Lemma 2.2(1) we clearly see that

holds for  . Therefore,
. Therefore,  is strictly logarithmically completely monotonic on
is strictly logarithmically completely monotonic on  that follows from (3.4) and (3.5).
that follows from (3.4) and (3.5).
Conversely, if  , then we can divide the set
, then we can divide the set  into two subsets:
into two subsets:  and
and  . Therefore, it follows from Lemma 2.2(2) and (3) that
. Therefore, it follows from Lemma 2.2(2) and (3) that  is not strictly logarithmically completely monotonic on
is not strictly logarithmically completely monotonic on  for
for  .
.
-
(2)
If
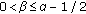 , then from (3.1) and (2.20) we get
, then from (3.1) and (2.20) we get 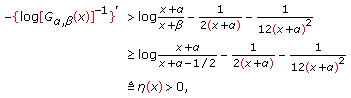 (3.6)
(3.6)
since

For  , it follows from (3.2) that
, it follows from (3.2) that

where  is defined as (3.3).
is defined as (3.3).
Therefore,  is strictly logarithmically completely monotonic on
is strictly logarithmically completely monotonic on  that follows from (3.6), (3.8), and Lemma 2.2(2).
that follows from (3.6), (3.8), and Lemma 2.2(2).
Conversely, if  and
and  , then we can divide the set
, then we can divide the set  into two subsets:
into two subsets:  and
and  . Therefore, it follows from Lemma 2.2(1) and (3) that
. Therefore, it follows from Lemma 2.2(1) and (3) that  is not strictly logarithmically completely monotonic on
is not strictly logarithmically completely monotonic on  for
for  .
.
Remark 1.
Although the upper and lower bounds of Kershaw's inequalities given in (1.11) and (1.12) are not better than those of inequalities in (1.4) and (1.5), the difference between them is close to zero as  is large enough. For example,
is large enough. For example,

Furthermore, the advantage of our inequalities is to give the upper and lower bounds of Kershaw's inequality for  and
and  while Laforgia established only one side of Kershaw's inequality.
while Laforgia established only one side of Kershaw's inequality.
References
Whittaker ET, Watson GN: A Course of Modern Analysis. Cambridge University Press, Cambridge, UK; 1996:vi+608.
Chu YM, Zhang XM, Zhang Z: The geometric convexity of a function involving gamma function with applications. Korean Mathematical Society 2010, 25(3):373–383. 10.4134/CKMS.2010.25.3.373
Zhang XM, Chu YM: A double inequality for gamma function. Journal of Inequalities and Applications 2009, 2009:-7.
Zhao T-H, Chu Y-M, Jiang Y-P: Monotonic and logarithmically convex properties of a function involving gamma functions. Journal of Inequalities and Applications 2009, 2009:-13.
Zhang XM, Chu YM: An inequality involving the gamma function and the psi function. International Journal of Modern Mathematics 2008, 3(1):67–73.
Chu YM, Zhang XM, Tang X: An elementary inequality for psi function. Bulletin of the Institute of Mathematics. Academia Sinica 2008, 3(3):373–380.
Song YQ, Chu YM, Wu L: An elementary double inequality for gamma function. International Journal of Pure and Applied Mathematics 2007, 38(4):549–554.
Chen Ch-P: Monotonicity and convexity for the gamma function. Journal of Inequalities in Pure and Applied Mathematics 2005, 6(4):6, article no. 100.
Guo B-N, Qi F: Two new proofs of the complete monotonicity of a function involving the PSI function. Bulletin of the Korean Mathematical Society 2010, 47(1):103–111. 10.4134/BKMS.2010.47.1.103
Chen Ch-P, Qi F, Srivastava HM: Some properties of functions related to the gamma and psi functions. Integral Transforms and Special Functions 2010, 21(1–2):153–164.
Qi F: A completely monotonic function involving the divided difference of the psi function and an equivalent inequality involving sums. The ANZIAM Journal 2007, 48(4):523–532. 10.1017/S1446181100003199
Qi F, Guo B-N: Monotonicity and convexity of ratio between gamma functions to different powers. Journal of the Indonesian Mathematical Society 2005, 11(1):39–49.
Chen Ch-P, Qi F: Inequalities relating to the gamma function. The Australian Journal of Mathematical Analysis and Applications 2004, 1(1, article no. 3):-7.
Guo B-N, Qi F: Inequalities and monotonicity for the ratio of gamma functions. Taiwanese Journal of Mathematics 2003, 7(2):239–247.
Qi F: Monotonicity results and inequalities for the gamma and incomplete gamma functions. Mathematical Inequalities & Applications 2002, 5(1):61–67.
Qi F, Mei J-Q: Some inequalities of the incomplete gamma and related functions. Zeitschrift für Analysis und Ihre Anwendungen 1999, 18(3):793–799.
Qi F, Guo S-L: Inequalities for the incomplete gamma and related functions. Mathematical Inequalities & Applications 1999, 2(1):47–53.
Alzer H: Some gamma function inequalities. Mathematics of Computation 1993, 60(201):337–346. 10.1090/S0025-5718-1993-1149288-7
Alzer H: On some inequalities for the gamma and psi functions. Mathematics of Computation 1997, 66(217):373–389. 10.1090/S0025-5718-97-00807-7
Anderson GD, Qiu S-L: A monotoneity property of the gamma function. Proceedings of the American Mathematical Society 1997, 125(11):3355–3362. 10.1090/S0002-9939-97-04152-X
Kershaw D: Some extensions of W. Gautschi's inequalities for the gamma function. Mathematics of Computation 1983, 41(164):607–611.
Merkle M: Logarithmic convexity and inequalities for the gamma function. Journal of Mathematical Analysis and Applications 1996, 203(2):369–380. 10.1006/jmaa.1996.0385
Alzer H, Berg Ch: Some classes of completely monotonic functions. II. The Ramanujan Journal 2006, 11(2):225–248. 10.1007/s11139-006-6510-5
Alzer H: Sharp inequalities for the digamma and polygamma functions. Forum Mathematicum 2004, 16(2):181–221. 10.1515/form.2004.009
Alzer H, Batir N: Monotonicity properties of the gamma function. Applied Mathematics Letters 2007, 20(7):778–781. 10.1016/j.aml.2006.08.026
Clark WE, Ismail MEH: Inequalities involving gamma and psi functions. Analysis and Applications 2003, 1(1):129–140. 10.1142/S0219530503000041
Elbert Á, Laforgia A: On some properties of the gamma function. Proceedings of the American Mathematical Society 2000, 128(9):2667–2673. 10.1090/S0002-9939-00-05520-9
Bustoz J, Ismail MEH: On gamma function inequalities. Mathematics of Computation 1986, 47(176):659–667. 10.1090/S0025-5718-1986-0856710-6
Ismail MEH, Lorch L, Muldoon ME: Completely monotonic functions associated with the gamma function and its -analogues. Journal of Mathematical Analysis and Applications 1986, 116(1):1–9. 10.1016/0022-247X(86)90042-9
Babenko VF, Skorokhodov DS: On Kolmogorov-type inequalities for functions defined on a semi-axis. Ukrainian Mathematical Journal 2007, 59(10):1299–1312.
Muldoon ME: Some monotonicity properties and characterizations of the gamma function. Aequationes Mathematicae 1978, 18(1–2):54–63. 10.1007/BF01844067
Qi F, Yang Q, Li W: Two logarithmically completely monotonic functions connected with gamma function. Integral Transforms and Special Functions 2006, 17(7):539–542. 10.1080/10652460500422379
Qi F, Niu D-W, Cao J: Logarithmically completely monotonic functions involving gamma and polygamma functions. Journal of Mathematical Analysis and Approximation Theory 2006, 1(1):66–74.
Qi F, Chen S-X, Cheung W-S: Logarithmically completely monotonic functions concerning gamma and digamma functions. Integral Transforms and Special Functions 2007, 18(5–6):435–443.
Qi F: A class of logarithmically completely monotonic functions and the best bounds in the first Kershaw's double inequality. Journal of Computational and Applied Mathematics 2007, 206(2):1007–1014. 10.1016/j.cam.2006.09.005
Chen Ch-P, Qi F: Logarithmically complete monotonicity properties for the gamma functions. The Australian Journal of Mathematical Analysis and Applications 2005, 2(2, article no. 8):-9.
Chen Ch-P, Qi F: Logarithmically completely monotonic functions relating to the gamma function. Journal of Mathematical Analysis and Applications 2006, 321(1):405–411. 10.1016/j.jmaa.2005.08.056
Chen Ch-P, Wang G, Zhu H: Two classes of logarithmically completely monotonic functions associated with the gamma function. Computational Intelligence Foundations and Applications 2010, 4: 168–173.
Chen Ch-P: Complete monotonicity properties for a ratio of gamma functions. Univerzitet u Beogradu. Publikacije Elektrotehničkog Fakulteta. Serija Matematika 2005, 16: 26–28.
Merkle M: On log-convexity of a ratio of gamma functions. Univerzitet u Beogradu. Publikacije Elektrotehničkog Fakulteta. Serija Matematika 1997, 8: 114–119.
Li A-J, Chen Ch-P: Some completely monotonic functions involving the gamma and polygamma functions. Journal of the Korean Mathematical Society 2008, 45(1):273–287. 10.4134/JKMS.2008.45.1.273
Qi F, Niu D-W, Cao J, Chen S-X: Four logarithmically completely monotonic functions involving gamma function. Journal of the Korean Mathematical Society 2008, 45(2):559–573. 10.4134/JKMS.2008.45.2.559
Laforgia A: Further inequalities for the gamma function. Mathematics of Computation 1984, 42(166):597–600. 10.1090/S0025-5718-1984-0736455-1
Elezović N, Giordano C, Pečarić J: The best bounds in Gautschi's inequality. Mathematical Inequalities & Applications 2000, 3(2):239–252.
Qi F, Guo B-N, Chen Ch-P: The best bounds in Gautschi-Kershaw inequalities. Mathematical Inequalities & Applications 2006, 9(3):427–436.
Guo S: Monotonicity and concavity properties of some functions involving the gamma function with applications. Journal of Inequalities in Pure and Applied Mathematics 2006, 7(2, article no. 45):-7.
Qi F, Guo B-N: A new proof of complete monotonicity of a function involving psi function. RGMIA Research Report Collection 2008., 11(3, article no. 12):
Acknowledgment
This work was supported by the National Science Foundation of China under Grant no. 11071069 and the Natural Science Foundation of Zhejiang Province under Grant no. Y7080106.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhao, TH., Chu, YM. A Class of Logarithmically Completely Monotonic Functions Associated with a Gamma Function. J Inequal Appl 2010, 392431 (2010). https://doi.org/10.1155/2010/392431
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/392431

 . Otherwise,
. Otherwise,  . The red curve is the graph of
. The red curve is the graph of  with an asymptotic line
with an asymptotic line  .
. , then we divide the proof into two cases.
, then we divide the proof into two cases. , then from Figure
, then from Figure  could be positive or negative. We divide the proof into two cases.
could be positive or negative. We divide the proof into two cases.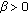 and
and 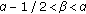 , then from (2.12) we clearly know that
, then from (2.12) we clearly know that  . Thus there exists
. Thus there exists  such that
such that 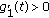 for
for  . It follows from (2.10) that
. It follows from (2.10) that  ,
, 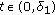 . Since
. Since  as
as 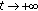 , we know that there exists
, we know that there exists 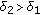 such that
such that 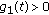 for
for  , which implies that
, which implies that 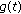 is strictly increasing on
is strictly increasing on  and
and 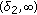 . Therefore,
. Therefore, 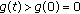 for
for 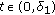 and
and 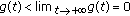 for
for 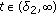 .
.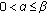 , then it follows from (3.1) and (2.20) that
, then it follows from (3.1) and (2.20) that 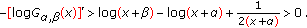
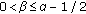 , then from (3.1) and (2.20) we get
, then from (3.1) and (2.20) we get